Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Методы условной оптимизации
Содержание
- 1. Методы условной оптимизации
- 2. 08/13/2019Постановка задачНайти минимум функцииПри ограничениях
- 3. 08/13/2019Условия типа равенстввыделяют в пространстве некоторую гиперповерхность
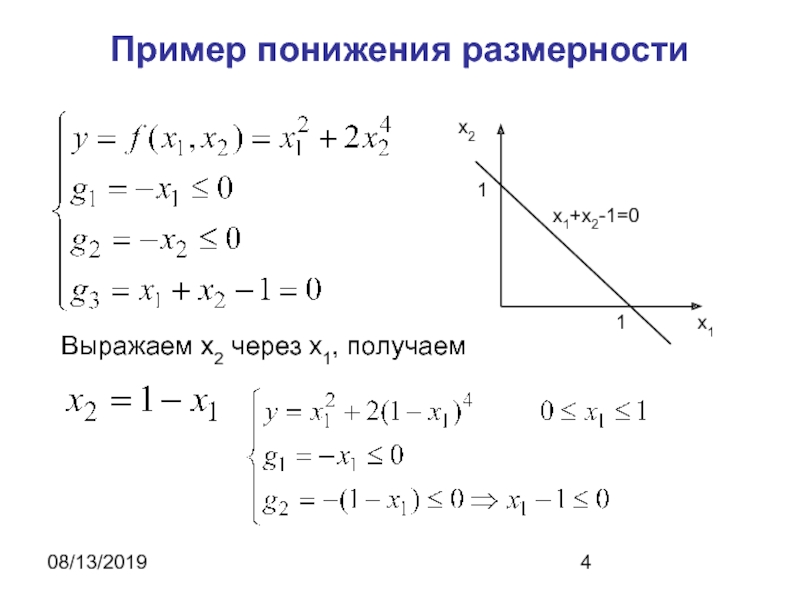
- 4. 08/13/2019Пример понижения размерностиВыражаем x2 через x1, получаем
- 5. 08/13/2019Условия типа неравенстввыделяют n - мерную область D, ограниченную гиперповерхностями
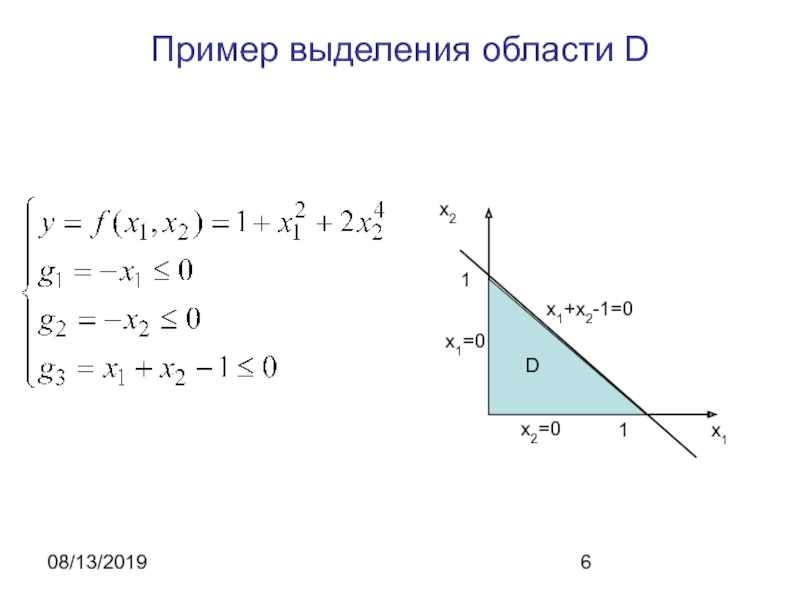
- 6. 08/13/2019Пример выделения области D
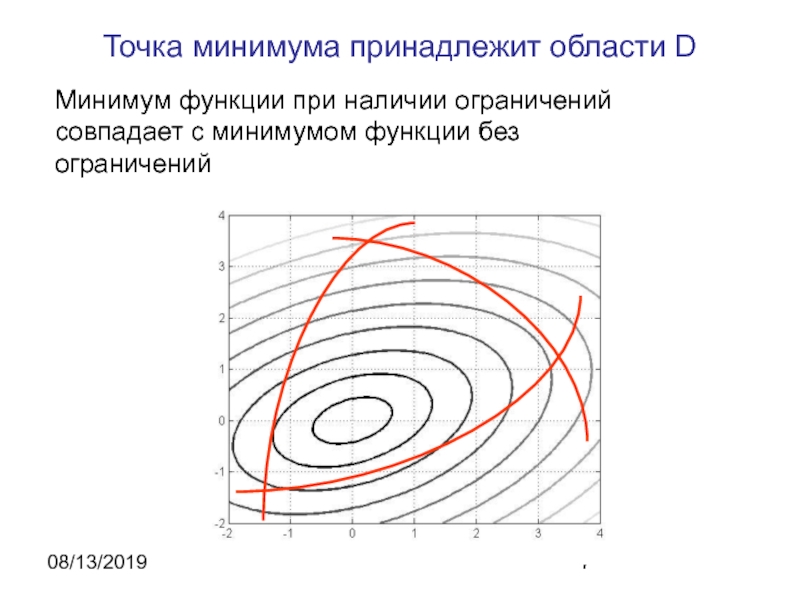
- 7. 08/13/2019Точка минимума принадлежит области DМинимум функции при наличии ограничений совпадает с минимумом функции без ограничений
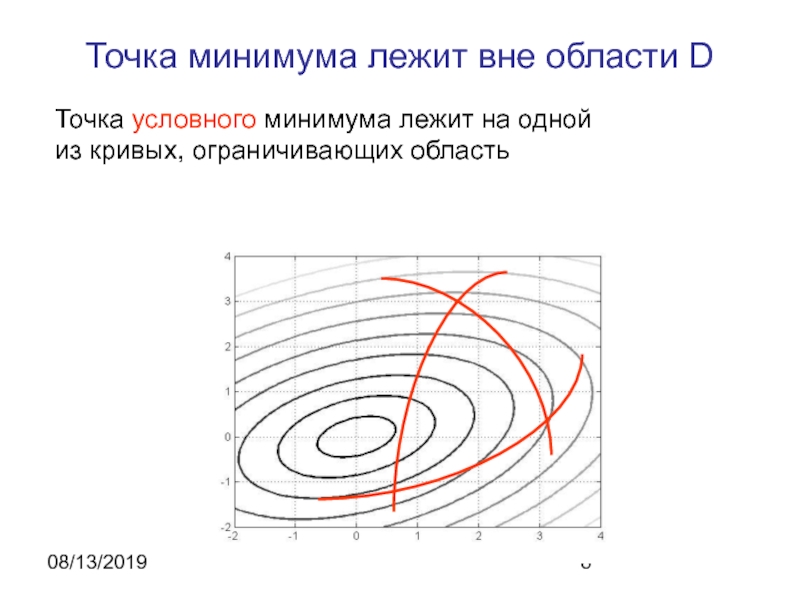
- 8. 08/13/2019Точка минимума лежит вне области DТочка условного минимума лежит на одной из кривых, ограничивающих область
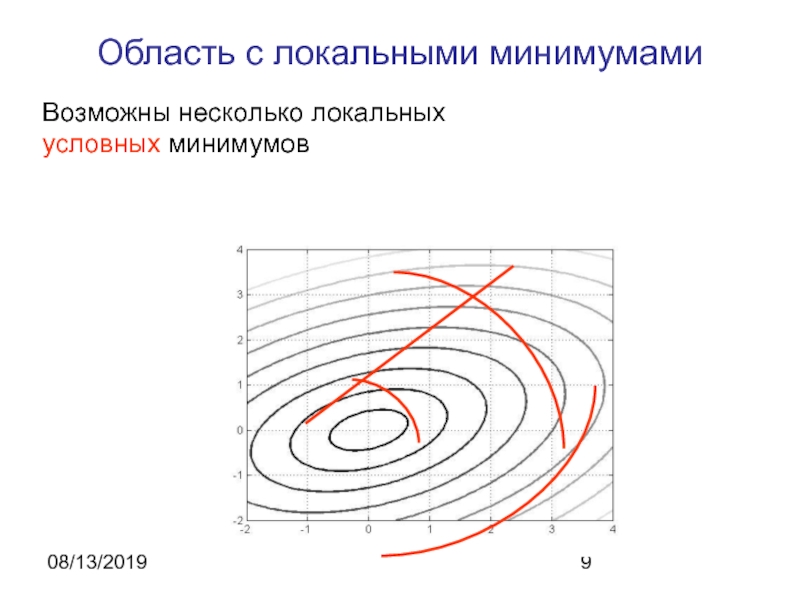
- 9. 08/13/2019Область с локальными минимумамиВозможны несколько локальных условных минимумов
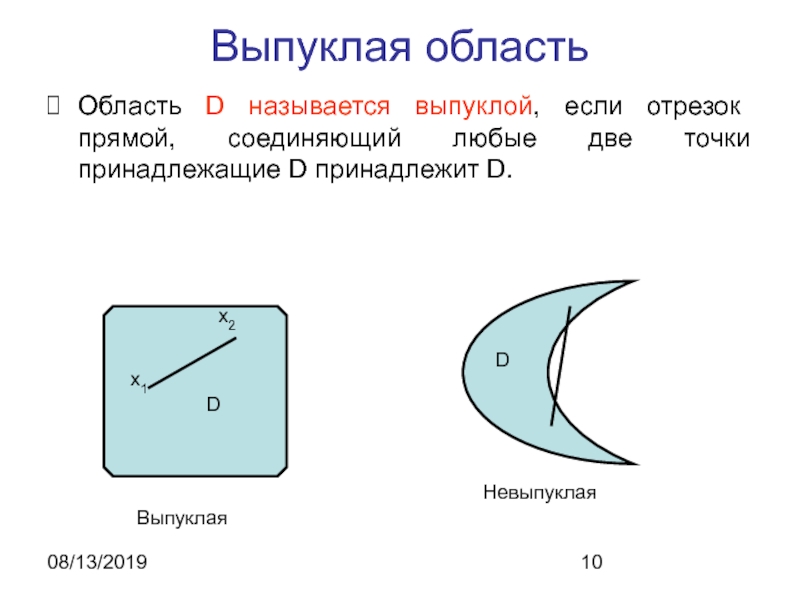
- 10. 08/13/2019Выпуклая областьОбласть D называется выпуклой, если отрезок
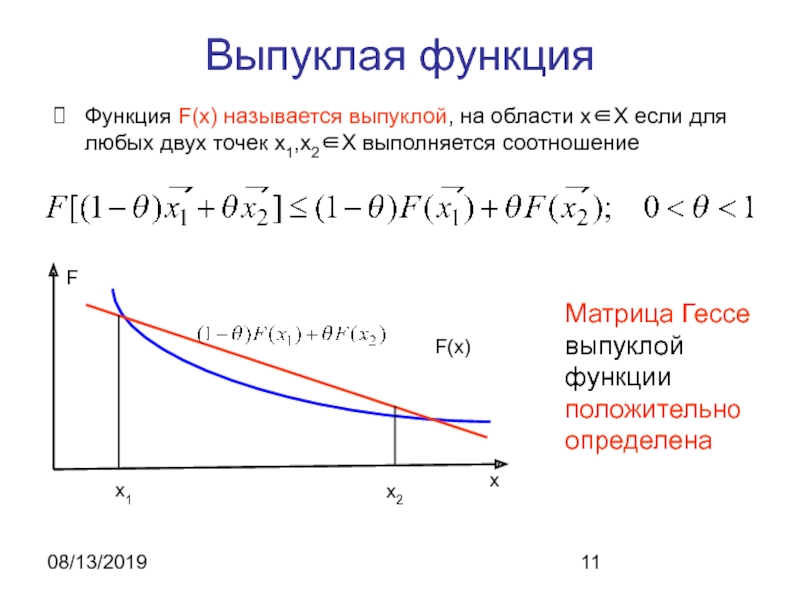
- 11. 08/13/2019Выпуклая функцияФункция F(x) называется выпуклой, на области
- 12. 08/13/2019Условие выпуклости областиДля того чтобы область D
- 13. 08/13/2019Метод штрафных функцийНапомним постановку задачиНайти минимум функцииПри ограничениях
- 14. 08/13/2019Метод штрафных функцийВведем следующую вспомогательную функцию
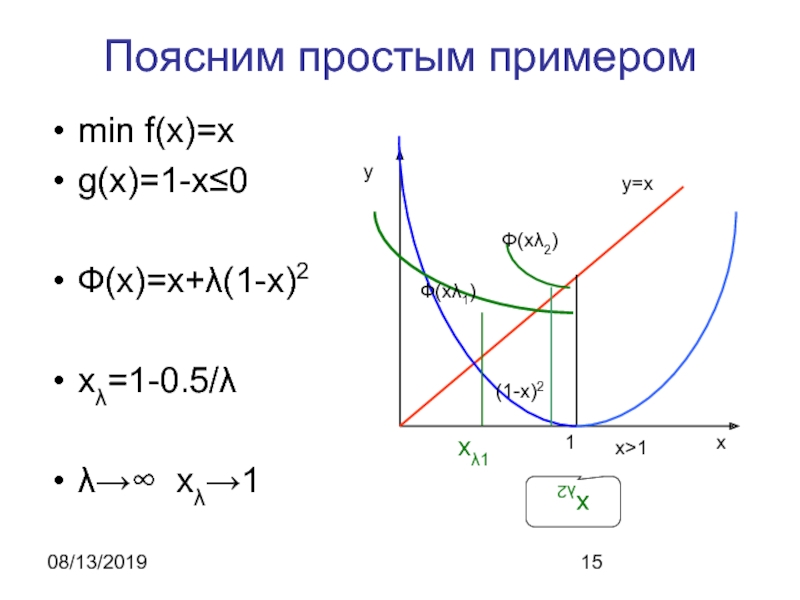
- 15. 08/13/2019Поясним простым примеромmin f(x)=xg(x)=1-x≤0Ф(x)=x+λ(1-x)2xλ=1-0.5/λλ→∞ xλ→1
- 16. 08/13/2019Программная реализациянахождение минимума функции одной переменной function
- 17. 08/13/2019нахождение минимума функции двух переменныхfunction optimglobal x0;x0=0.3options
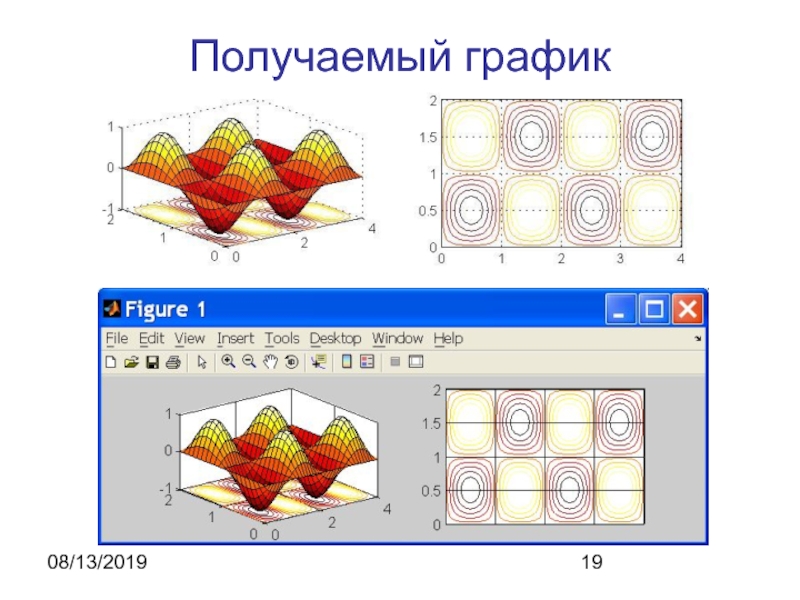
- 18. 08/13/2019Графическое исследование двумерной функцииfunction grf;[x,y]= meshgrid(0:0.1:4,0:0.1:2);z=-sin(pi*x).*sin(pi*y); subplot(1,2,1);surfc(x,y,z);%colormap(winter) subplot(1,2,2); %levels = 0:-0.1:-5;%contour(x,y,z,levels)contour(x,y,z,10)%colorbarcolormap(hot) %(jet) (hot) (winter)(gray)grid onreturn
- 19. 08/13/2019Получаемый график
- 20. 08/13/2019ВАРИАНТЫ ЗАДАНИЙ
- 21. Скачать презентанцию
08/13/2019Постановка задачНайти минимум функцииПри ограничениях
Слайды и текст этой презентации
Слайд 308/13/2019
Условия типа равенств
выделяют в пространстве некоторую гиперповерхность размерности p. Используя
Слайд 508/13/2019
Условия типа неравенств
выделяют n - мерную область D, ограниченную гиперповерхностями
Слайд 708/13/2019
Точка минимума принадлежит области D
Минимум функции при наличии ограничений совпадает
с минимумом функции без ограничений
Слайд 808/13/2019
Точка минимума лежит вне области D
Точка условного минимума лежит на
одной из кривых, ограничивающих область
Слайд 1008/13/2019
Выпуклая область
Область D называется выпуклой, если отрезок прямой, соединяющий любые
две точки принадлежащие D принадлежит D.
Выпуклая
Невыпуклая
Слайд 1108/13/2019
Выпуклая функция
Функция F(x) называется выпуклой, на области x∈X если для
любых двух точек x1,x2∈X выполняется соотношение
x
F
F(x)
x2
x1
Матрица Гессе выпуклой функции
положительно определена
Слайд 1208/13/2019
Условие выпуклости области
Для того чтобы область D описанная неравенствами
была
выпуклой,
необходимо, чтобы функции gk(x) , были выпуклыми.
Если целевая функция
f и область D выпуклы, то приходим к задаче выпуклого программирования, для которой справедлива вся нижеприведенная теория 
Слайд 1308/13/2019
Метод штрафных функций
Напомним постановку задачи
Найти минимум функции
При ограничениях
Слайд 1608/13/2019
Программная реализация
нахождение минимума функции одной переменной
function optim
global x0;
x0=2
xmim=fminbnd(@foc,-5.0,5.0)
function y=foc(x);
global
x0;
y=(x-x0).^2; %здесь записывается своя функция
return
Результат:
x0 =
2
xmim
=2
Слайд 1708/13/2019
нахождение минимума функции двух переменных
function optim
global x0;
x0=0.3
options = optimset('Display','iter','TolX',1.0e-3);
[xmim,fmin]=fminsearch(@foc,[1.0,1.5],options)
function y=foc(x);
global
x0; %передача x0 внутрь функции
x1=x(1);
x2=x(2);
y=-sin(pi*(x1-x0)).*sin(pi*x2);
return
![08/13/2019нахождение минимума функции двух переменныхfunction optimglobal x0;x0=0.3options = optimset('Display','iter','TolX',1.0e-3);[xmim,fmin]=fminsearch(@foc,[1.0,1.5],options)function y=foc(x);global x0; %передача](/img/thumbs/9fa749fc67424fe3504fa2661cc62a97-800x.jpg "Методы условной оптимизации 08/13/2019нахождение минимума функции двух переменныхfunction optimglobal x0;x0=0.3options = optimset('Display','iter','TolX',1.0e-3);[xmim,fmin]=fminsearch(@foc,[1.0,1.5],options)function y=foc(x);global x0;")
Слайд 1808/13/2019
Графическое исследование двумерной функции
function grf;
[x,y]= meshgrid(0:0.1:4,0:0.1:2);
z=-sin(pi*x).*sin(pi*y);
subplot(1,2,1);
surfc(x,y,z);
%colormap(winter)
subplot(1,2,2);
%levels =
0:-0.1:-5;
%contour(x,y,z,levels)
contour(x,y,z,10)
%colorbar
colormap(hot) %(jet) (hot) (winter)(gray)
grid on
return
![08/13/2019Графическое исследование двумерной функцииfunction grf;[x,y]= meshgrid(0:0.1:4,0:0.1:2);z=-sin(pi*x).*sin(pi*y); subplot(1,2,1);surfc(x,y,z);%colormap(winter) subplot(1,2,2); %levels = 0:-0.1:-5;%contour(x,y,z,levels)contour(x,y,z,10)%colorbarcolormap(hot) %(jet) (hot) (winter)(gray)grid onreturn](/img/thumbs/1e9a4ba88dbb2a0ecc819bd70e7bedcb-800x.jpg "Методы условной оптимизации 08/13/2019Графическое исследование двумерной функцииfunction grf;[x,y]= meshgrid(0:0.1:4,0:0.1:2);z=-sin(pi*x).*sin(pi*y); subplot(1,2,1);surfc(x,y,z);%colormap(winter) subplot(1,2,2); %levels = 0:-0.1:-5;%contour(x,y,z,levels)contour(x,y,z,10)%colorbarcolormap(hot) %(jet) (hot) (winter)(gray)grid onreturn")
