Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Методы зондирования окружающей среды Лабораторная работа Оценка погрешности
Содержание
- 1. Методы зондирования окружающей среды Лабораторная работа Оценка погрешности
- 2. Цель работы: 1. Исследовать влияние погрешности в задании
- 3. Материалы для работы: 1. Программа, содержащаяся в файле «VarTz-#. xls». 2. Набор исходных параметров, задаваемых преподавателем.
- 4. Краткие сведения из теории
- 5. Для оценки погрешности определения температуры подстилающей поверхности
- 6. Каждый из указанных 4 параметров (соответственно: излучательной
- 7. «Аналитический» подход к оценке погрешности определения Ts
- 8. Слайд 8
- 9. Слайд 9
- 10. Слайд 10
- 11. Первый подход (метод разностей) более точен и не требует выполнения условия x
- 12. «Статистический» подход к оценке погрешности определения Ts
- 13. 3. Метод Monte-Carlo Метод Монте-Карло или метод статистических
- 14. Генерация псевдослучайных чисел Специальный оператор RND (Random
- 15. Генерация псевдослучайных чисел Специальный оператор RND (Random
- 16. Нормальный закон распределения (закон Гаусса). Непрерывная случайная
- 17. Для расчета методом суперпозиции двух значений случайной
- 18. Для исследования влияния случайных погрешностей в задании
- 19. Собственно метод Монте-Карло при решении рассматриваемой задачи
- 20. В данной работе для оценки погрешности определения
- 21. Порядок выполнения работы
- 22. Изучить описание данной работы, обращаясь в случае
- 23. Рис. 4. Индикация входных параметров программыРис. 5. Результаты расчета значений интенсивности уходящего излучения и яркостной температуры
- 24. Рис. 6. Результаты расчета относительных погрешностей [%]
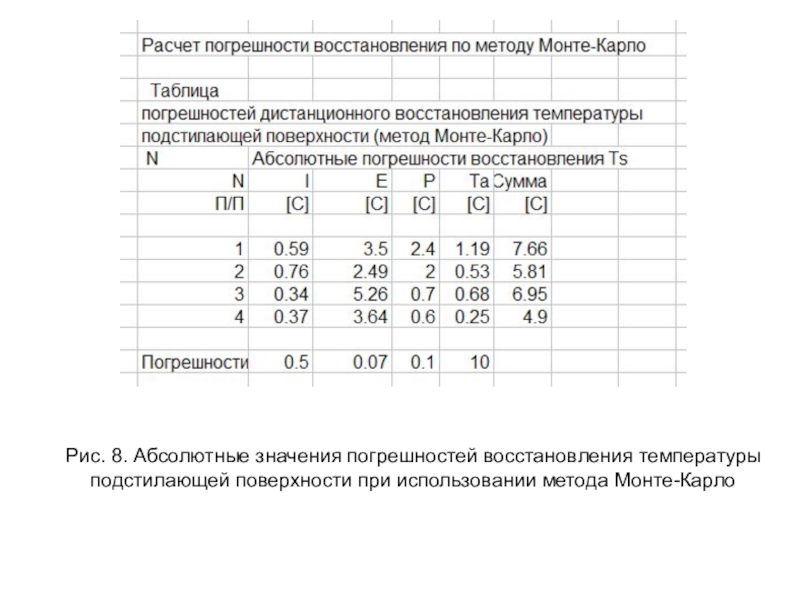
- 25. Рис. 8. Абсолютные значения погрешностей восстановления температуры подстилающей поверхности при использовании метода Монте-Карло
- 26. Рис. 9. Абсолютные значения погрешностей восстановления температуры
- 27. Рис. 10. Абсолютные значения погрешностей восстановления температуры
- 28. Рис. 11. Пояснительные сведения на Листе 2
- 29. Рис. 12. Пояснительные сведения на Листе 2
- 30. Рис. 13. Пояснительные сведения на Листе 2
- 31. Составить план проведения необходимых расчетов для оценки
- 32. Составить отчет по данной работе, отражающий основные
- 33. Рис. 3. Пример работы с информационными и
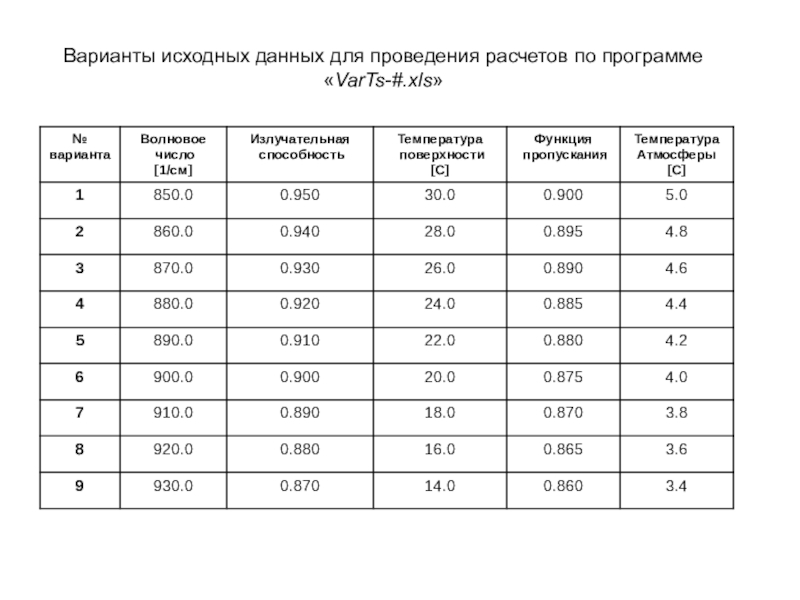
- 34. Варианты исходных данных для проведения расчетов по программе «VarTs-#.xls»
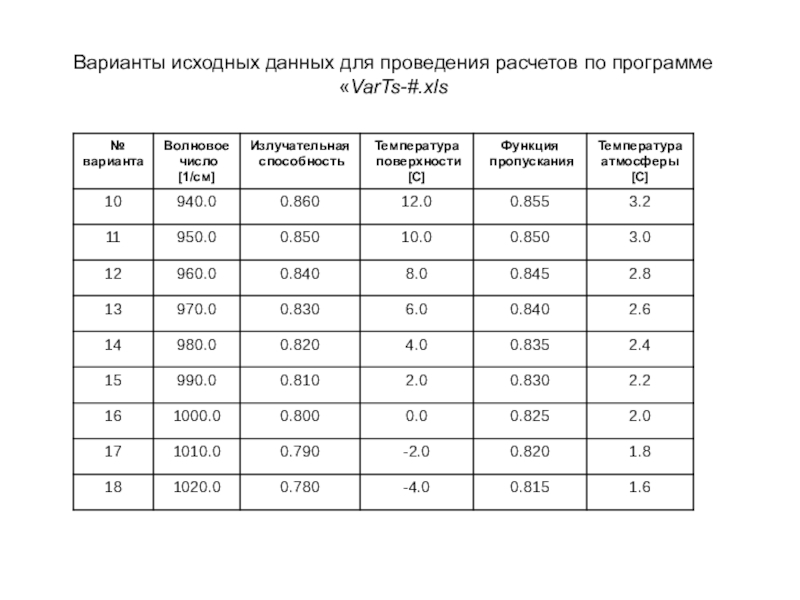
- 35. Варианты исходных данных для проведения расчетов по программе «VarTs-#.xls
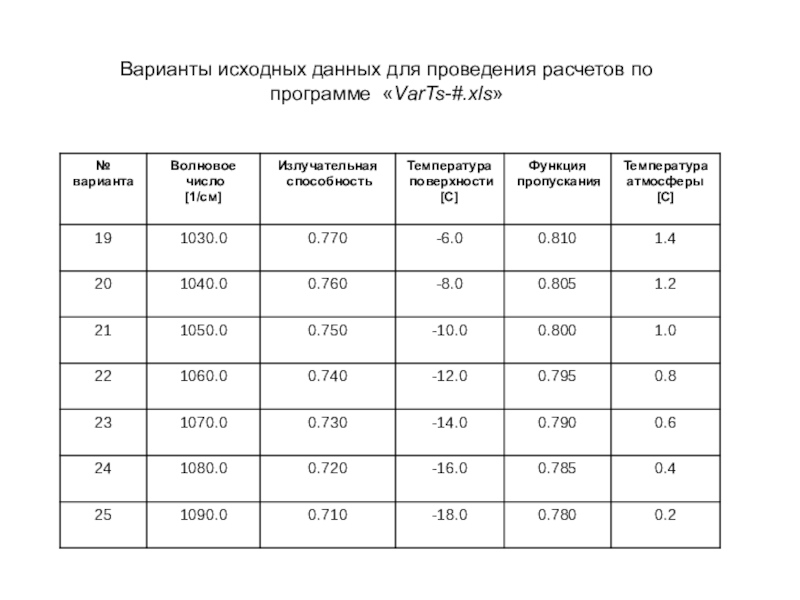
- 36. Варианты исходных данных для проведения расчетов по программе «VarTs-#.xls»
- 37. Контрольные вопросы1. От точности задания каких параметров
- 38. Литература
- 39. 1. А.Д. Кузнецов, В.В. Розанов, Ю.М. Тимофеев
- 40. 6. А.В. Васильев, И.Н. Мельникова Методы прикладного
- 41. Какие будут вопросы?
- 42. Пример применения метода Монте-Карло для решения не «статистической» задачи - расчету числа Пи
- 43. The process with using random numbers for
- 44. Test if the dart hits to the
- 45. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1
Методы зондирования окружающей среды
Лабораторная работа
Оценка погрешности измерения Ts
Профессор
Кузнецов Анатолий Дмитриевич
Слайд 2Цель работы:
1. Исследовать влияние погрешности в задании исходных данных на
точность дистанционного измерения температуры подстилающей поверхности Ts спутниковым радиометром.
Слайд 3Материалы для работы:
1. Программа, содержащаяся в файле «VarTz-#. xls».
2.
Набор исходных параметров, задаваемых преподавателем.
Слайд 5 Для оценки погрешности определения температуры подстилающей поверхности рассмотрим соотношение, используемое
для расчета температуры подстилающей поверхности по измерениям уходящего теплового излучения
в «окнах» прозрачности:как функцию четырех переменных:
где
Слайд 6 Каждый из указанных 4 параметров (соответственно: излучательной способности подстилающей поверхности,
интенсивности уходящего излучения, функции пропускания всей толщи атмосферы и «эффективной»
температуры атмосферы)может быть задан (или измерен) с некоторой погрешность:
Рассмотрим, как можно количественно оценить влияние погрешности в задании этих 4 параметров на точность дистанционного измерения Ts.
Слайд 8
Метод разностей.
Для функции одной переменной f(x) при известном точном значении аргумента x0 и известной погрешности его задания x ошибка определения значения функции f будет равна :
(5.3)
Для функции нескольких переменных соотношение (5.3) может последовательно применяться к каждой переменной.
Можно и одновременно задавать погрешности для всех M переменных x(i) и в этом случае
При расчете в формуле для ∆f параметр М = 4 и соответственно
Слайд 9
2. Метод производных.
Для функции одной переменной, разлагая ее в ряд Тейлора в окрестности точки x0, можно записать
(5.4)
При x <<1 в уравнении (5.4) можно отбросить все слагаемые кроме первого и тогда для оценки погрешности определения функции f(x) за счет задания точного значения аргумента x0 с погрешностью x можно записать
Слайд 10
При использовании метода производных для оценки точности дистанционного зондирования Ts можно записать
Взяв соответствующие производные, получаем в явном виде четыре слагаемых, входящих в формулу для оценки
где использованы следующие обозначения:
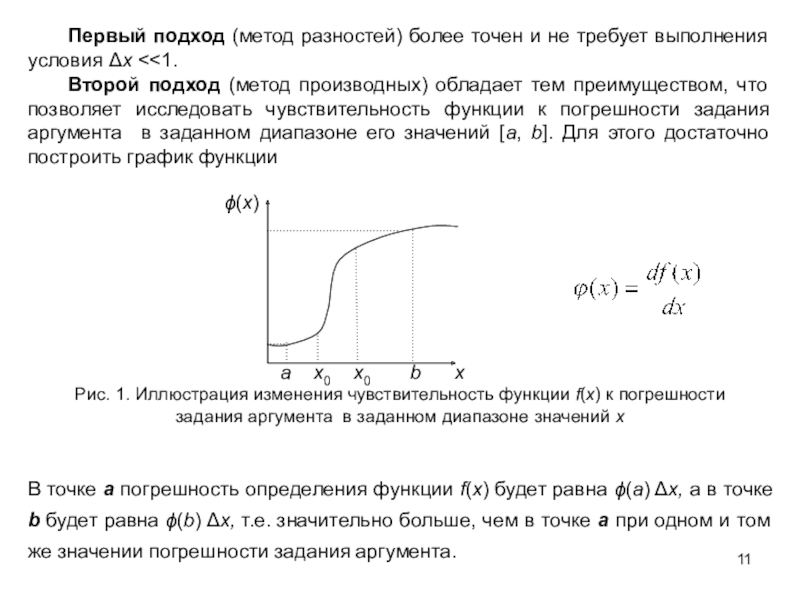
Слайд 11 Первый подход (метод разностей) более точен и не требует выполнения
условия x
что позволяет исследовать чувствительность функции к погрешности задания аргумента в заданном диапазоне его значений [a, b]. Для этого достаточно построить график функции(x)
a x0 x0 b x
В точке a погрешность определения функции f(x) будет равна (a) x, а в точке b будет равна (b) x, т.е. значительно больше, чем в точке а при одном и том же значении погрешности задания аргумента.
Рис. 1. Иллюстрация изменения чувствительность функции f(x) к погрешности задания аргумента в заданном диапазоне значений x
Слайд 133. Метод Monte-Carlo
Метод Монте-Карло или метод статистических испытаний это
численное решение математических задач при помощи моделирования случайных величин. Широкое
практическое использование этого метода стало возможно только благодаря появлению современных быстродействующих компьютеров.Основу метода Монте‑Карло составляет возможность получения случайных чисел с заданными статистическими характеристиками.
Числа, получаемые по какой-либо формуле и имитирующие значения случайной величины, называются псевдослучайными числами.
Слайд 14Генерация псевдослучайных чисел
Специальный оператор RND (Random Number Digitizer) включен
в состав большинства языков программирования. С его помощью генерируются псевдослучайные
числа, имеющие равномерный закон распределения на промежутке [0,1].Равномерное распределение. Непрерывная величина x распределена равномерно на интервале (a, b), если все ее возможные значения находятся на этом интервале и плотность распределения вероятностей p(x) на этом же интервале постоянна:
Рис. 2. Вид функции p(x) при равномерном законе распределения на промежутке [a,b]
Слайд 15Генерация псевдослучайных чисел
Специальный оператор RND (Random Number Digitizer) включен
в состав большинства языков программирования. С его помощью генерируются псевдослучайные
числа, имеющие равномерный закон распределения на промежутке [0,1].Преобразование по определенным методикам псевдослучайных чисел, имеющие равномерный закон распределения на промежутке [0,1], позволяет получить псевдослучайные числа с заданными законами распределения.
Поскольку при исследовании влияния погрешностей задания исходных данных на точность дистанционного измерения температуры подстилающей поверхности логично предположить, что эти погрешности имеют нормальный закон распределения, то рассмотрим один из возможных подходов к такому преобразованию с использованием псевдослучайных чисел с равномерным законом распределения.
Слайд 16 Нормальный закон распределения (закон Гаусса). Непрерывная случайная величина Х имеет
нормальный закон распределения с параметрами Ϭ и μ, если ее
плотность распределения вероятностей имеет вид:Рис. 3. Вид функции p(x) при нормальном законе распределения
Слайд 17 Для расчета методом суперпозиции двух значений случайной величины ,
имеющих нормальный закон распределения с параметрами μ = 0 и
Ϭ = 1, может быть использован следующий алгоритм, использующий два псевдослучайных числа с равномерным законом распределения γ1 и γ2:На основе этих соотношений расчет псевдослучайного числа , имеющей нормальное распределение, но уже с параметрами:
среднее значение и дисперсия
может быть произведена на основе следующего соотношения:
Слайд 18 Для исследования влияния случайных погрешностей в задании исходных данных на
точность дистанционного измерения температуры подстилающей поверхности необходимо вычислить «реакцию» математической
модели на погрешности, задаваемые случайным образом в значениях параметров, от которых эта модель зависит.Слайд 19 Собственно метод Монте-Карло при решении рассматриваемой задачи заключается в следующем:
-
в многократном расчете (моделировании) входящих в формулу для
значений погрешностей в задании 4 параметров, имеющих нормальное распределение с заданными средними значениями и дисперсиями- в многократном расчет методами разностей (или производных) значений
- в последующим расчете статистических характеристик полученных погрешностей дистанционного измерения температуры подстилающей поверхности (средней погрешности, среднеквадратичного отклонения погрешностей от среднего значения, гистограммы распределения погрешностей и др.).
Слайд 20 В данной работе для оценки погрешности определения Ts методом Монте-Карло
используется подход, определяемый соотношениями Метод Монте-Карло заключается в многократном моделировании
значений 0, имеющих нормальное распределение с нулевым средним и заданную дисперсию (в программе вместо дисперсии задается соответствующее среднеквадратичное отклонение). При расчете значений Ts используются формулыСлайд 22
Изучить описание данной работы, обращаясь в случае необходимости к учебным
пособиям, указанным в списке литературы.
Открыть файл «VarTs-#.xls».
3. Внимательно ознакомиться
с порядком и формой представления данных на Листе 1 и Листе 2 (см. следующие слайды).4. Получить у преподавателя номер варианта, необходимый для определения используемых при выполнении данной лабораторной работы параметров.
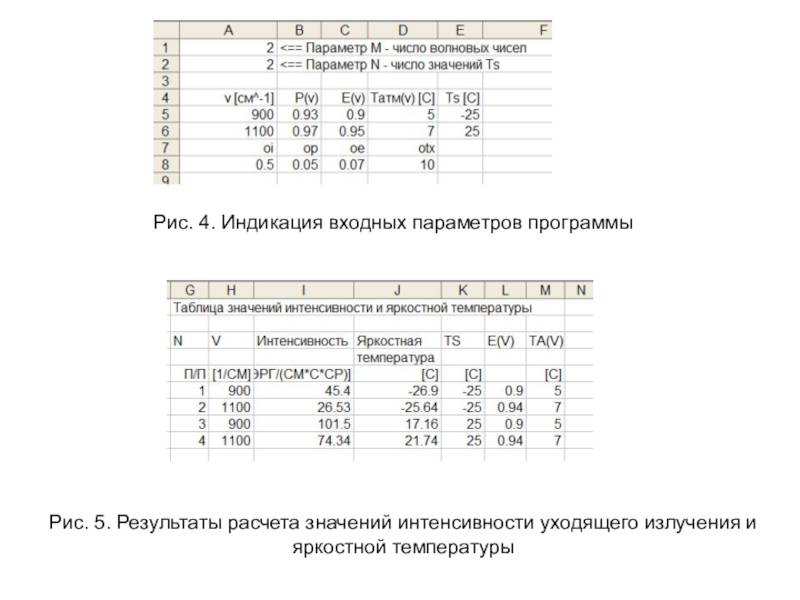
Слайд 23Рис. 4. Индикация входных параметров программы
Рис. 5. Результаты расчета значений
интенсивности уходящего излучения и яркостной температуры
Слайд 24Рис. 6. Результаты расчета относительных погрешностей [%] задания (измерения) интенсивностей
уходящего излучения (oi), функций пропускания (op), излучательной способности подстилающей поверхности
(oe) и «эффективной» температуры атмосферы (otx)Рис. 7. Абсолютные значения погрешностей восстановления температуры подстилающей поверхности при использовании метода производных
Слайд 25Рис. 8. Абсолютные значения погрешностей восстановления температуры подстилающей поверхности при
использовании метода Монте-Карло
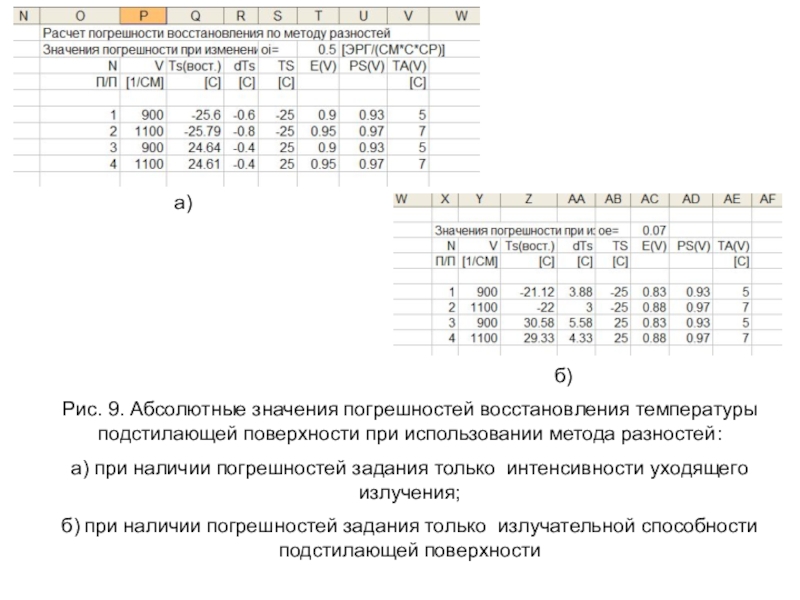
Слайд 26Рис. 9. Абсолютные значения погрешностей восстановления температуры подстилающей поверхности при
использовании метода разностей:
а) при наличии погрешностей задания только интенсивности
уходящего излучения; б) при наличии погрешностей задания только излучательной способности подстилающей поверхности
а)
б)
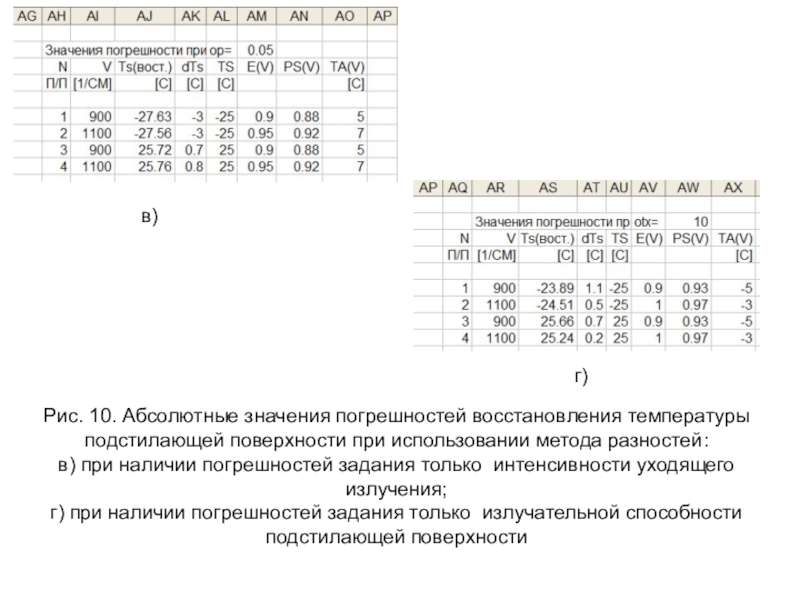
Слайд 27Рис. 10. Абсолютные значения погрешностей восстановления температуры подстилающей поверхности при
использовании метода разностей:
в) при наличии погрешностей задания только интенсивности
уходящего излучения; г) при наличии погрешностей задания только излучательной способности подстилающей поверхности
в)
г)
Слайд 31
Составить план проведения необходимых расчетов для оценки влияния погрешностей в
задании исходных данных на величину ∆Ts . Проведенная серия расчетов
должна позволить построить и исследовать график зависимости погрешности дистанционного измерения Ts от погрешности задания (измерения) исходных данных.Диапазон изменения величины погрешностей для каждого из 4 параметров определяется самостоятельно в процессе проведения численных экспериментов.
Слишком «маленькие» погрешности могут давать практически нулевые значения погрешности дистанционного измерения температуры подстилающей поверхности, а слишком «большие» погрешности – ошибки в определении Ts в десятки и сотни градусов, что, естественно, не имеет практического смысла.
Диапазон изменения вводимых погрешностей должен быть таким, чтобы для каждого из 4 параметров можно было бы по результатам расчетов построить графики зависимости ∆Ts от относительной погрешности каждого из 4 параметров, на котором величина ∆Ts менялась бы от 00 до 50. Причем на каждом графике должны быть три кривых, соответствующих трем методам расчета ∆Ts .
Слайд 32Составить отчет по данной работе, отражающий основные этапы проделанной работы
и полученные при этом результаты и выводы.
С использованием редактора EXCEL
построить графики зависимостей погрешностей восстановления температуры от заданных погрешностей начальных параметров. Провести анализу полученных результатов и, в частности:
- объяснить причину наличия различий в оценке ∆Ts, возникающих при использовании трех подходов (методов);
- определить, к относительным погрешностям какого из 4 параметров более «чувствительна» точность дистанционного измерения температуры подстилающей поверхности.
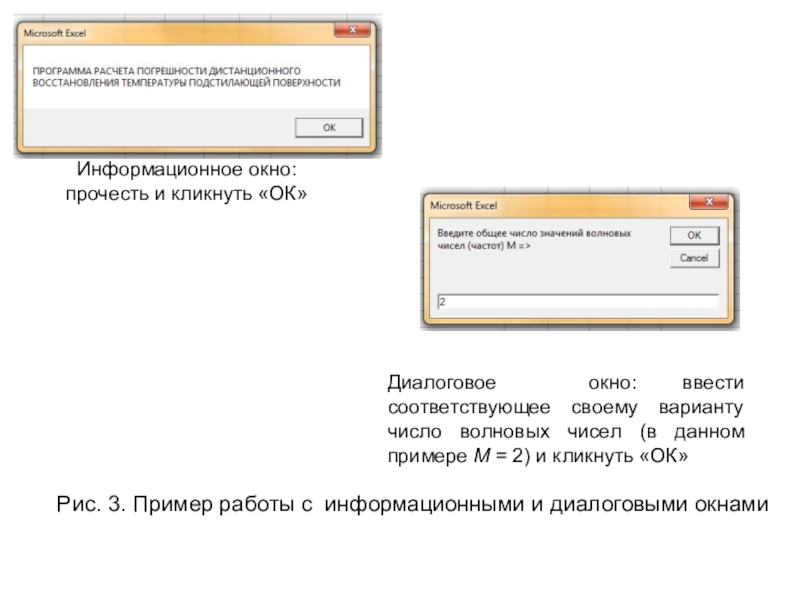
Слайд 33Рис. 3. Пример работы с информационными и диалоговыми окнами
Информационное окно:
прочесть и кликнуть «ОК»
Диалоговое окно: ввести соответствующее своему варианту число
волновых чисел (в данном примере М = 2) и кликнуть «ОК»Слайд 37Контрольные вопросы
1. От точности задания каких параметров зависит точность дистанционного
измерения температуры подстилающей поверхности ?
2. При каких допущениях было получено
используемое в данной работе соотношение для вычисления значения Ts ?3. От точности задания какого параметра (исходя из значения относительной погрешности) «сильнее» всего зависит точность дистанционного определения температуры подстилающей поверхности ?
4. Отличаются ли при одной и той же величине погрешности в задании исходных данных значения ошибок определения Ts, полученные с использованием рассмотренных в данной работе подходов и если отличаются, то почему?
5. От чего зависит точность оценки статистических характеристик погрешности определения Ts при использовании метода Монте-Карло ?
6. Какие способы получения алгоритмов для расчета псевдослучайных чисел с заданным законом распределения рассмотрены в данной работе?
Слайд 39
1. А.Д. Кузнецов, В.В. Розанов, Ю.М. Тимофеев Дистанционное зондирование атмосферы
тропической зоны. ─ Л., изд. ЛГМИ, 1988. ─ 90 с.
2. А.Д. Кузнецов, О.С. Сероухова Практикум по учебным дисциплинам «Дистанционное зондирование атмосферы» и «Теория переноса излучения в жидкостях и газах». ─ СПб., изд-во РГГМУ, 2000. ─ 126 с.
3. А.В.Васильев, А.Д. Кузнецов, И.Н. Мельникова. Дистанционное зондирование окружающей среды из космоса. Практикум. ─ СПб., изд-во БГТУ «Военмех», 2008. ─ 133 с.
4. Тимофеев Ю.М., Васильев А.В. Теоретичские основы атмосферной оптики. ─ СПб.: Наука, 2003 ─ 474 с.
5. Васильев А.В., Мельникова И.Н. Коротковолновое солнечное излучение в атмосфере Земли. Расчеты. Измерения. Интерпретация. Санкт-Петербург, НИИХ СПбГУ, 2002 388 с.
Слайд 40
6. А.В. Васильев, И.Н. Мельникова Методы прикладного анализа результатов натурных
измерений в окружающей среде. Учебное пособие. Монография. Изд-во БГТУ «Военмех».
2009. 370 с.7. Васильев А.В., Мельникова И.Н. Экспериментальные модели атмосферы и земной поверхности (Учебное пособие). Изд-во БГТУ «Военмех» 2010. 226 с.
8. Melnikova I., Vasilyev A. Short-wave solar radiation in the Earth atmosphere. Calculation. Observation. Interpretation. Springer-Verlag GmbH&Co.KG, Heidelberg, 2004. 350p
9. A. Kuznetsov, I. Melnikova, D. Pozdnyakov, O. Seroukhova, A. Vasilyev. Remote Sensing of the Environment and Radiation Transfer. An Introductory Survey. Springer-Verlag Berlin Heidelberg, 2011. 200p.
Слайд 42 Пример применения метода Монте-Карло для решения не «статистической» задачи -
расчету числа Пи
Слайд 43The process with using random numbers for calculating value of
Ssquare =1, Scircle = r2
= /4y
0 1 x
Throwing darts to the square many times
or
Find random numbers in the interval [0,1] :
x=RND they define the point in the square
y=RND.
Find many random point in the square. Amount of hitting to a region is proportional to the area of this region.
N ~Ssquare N1 ~ Scircle , then
/4 = N1/N , hence = 4 N1/N
It is to find the value N1 , with knowing the value N
Слайд 44Test if the dart hits to the circle or not
:
The mathematical model of throwing darts :
Radius is r =
0.5Then the radius-vector of the random point :
Compare it with the circle radius:
l 0.5 – the point is within circle, l > 0.5 the point is out of the circle
How much is it to be repeated?
It is defined by needed exactness:
One throwing:
1: within circle N1 = 1 ; N = 1, then = 4
2: out of circle N1 = 0 ; N = 1, then = 0, hence value of is in the interval [0,4]
10 throwings provide = 3.14
10 000 throwings provide value of to an accuracy of the fifth decimal place
(or to fife-place accuracy)





















![Методы зондирования окружающей среды Лабораторная работа Оценка погрешности Рис. 6. Результаты расчета относительных погрешностей [%] задания (измерения) интенсивностей уходящего Рис. 6. Результаты расчета относительных погрешностей [%] задания (измерения) интенсивностей уходящего излучения (oi), функций пропускания (op), излучательной](/img/thumbs/ffc3c3011b16627fbf86dbf6e926d752-800x.jpg)