Слайд 11.1 Гармонические колебания
ЛЕКЦИЯ 1. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ
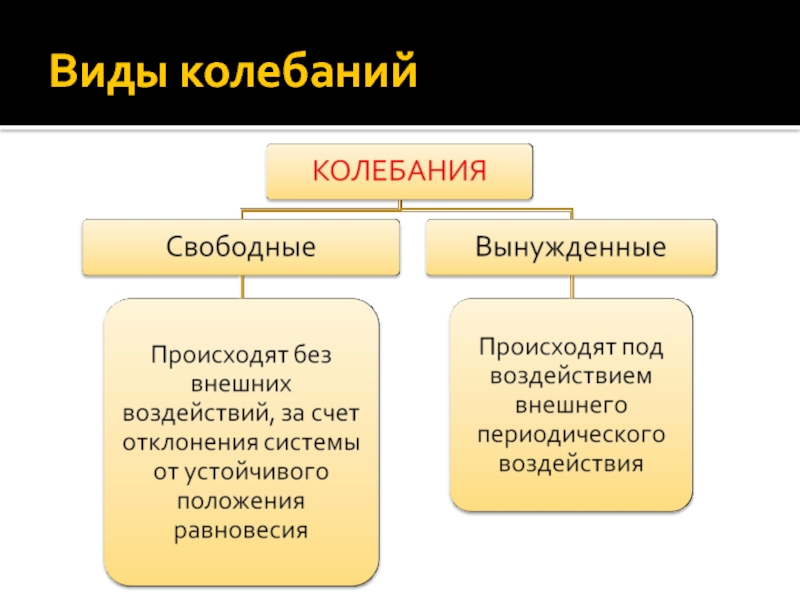
Слайд 2Колебания
Колебания – это такое изменения состояния системы, при котором ее
параметры меняются со временем по периодическому (или почти периодическому) закону.
Колебания
называются периодическими, если значения физических величин (параметров системы) повторяются через одинаковые промежутки времени.
Период колебаний T – тот наименьший промежуток времени, по истечении которого повторяются значения всех физических величин, характеризующих колебательное движение.
За время, равное периоду, совершается одно полное колебание
Слайд 3Колебания
Частотой (линейной частотой) ν периодических колебаний называют число колебаний, совершаемых
за единицу времени:
Частота колебаний измеряется в герцах (Гц): [ν] =
Гц = с-1.
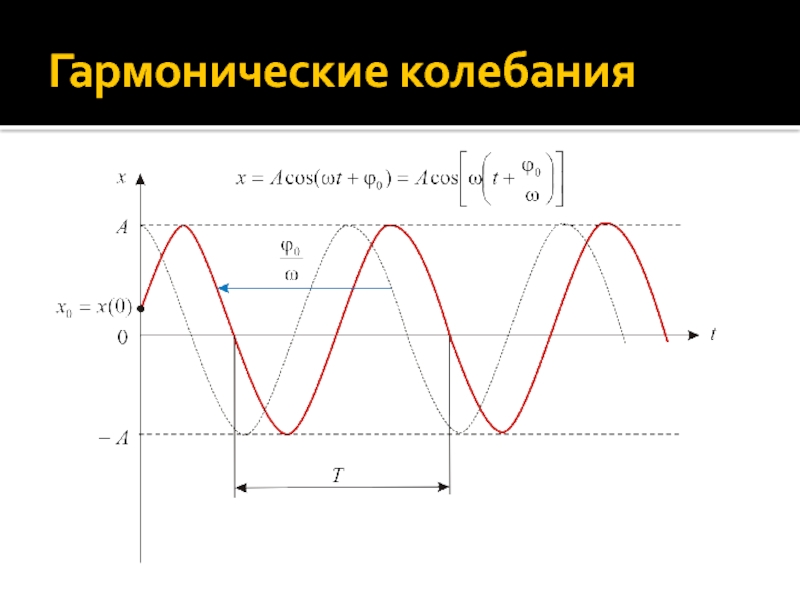
Слайд 5Гармонические колебания
Колебания величины x называются гармоническими, если эта величина меняется
со временем t по закону:
Величина A (измеряется в тех же
единицах, что и x) – амплитуда колебаний – максимальное отклонение колеблющейся величины x от положения устойчивого равновесия (A = max x).
ω – циклическая (круговая) частота колебаний (определяется только параметрами системы); [ω] = c-1.
Слайд 6Гармонические колебания
Величина ϕ = ωt + ϕ0 называется фазой колебаний.
Косинус (или синус) этой величины показывает, во сколько раз значение
физической величины x меньше его амплитудного (максимального) значения в данный момент времени.
Величина ϕ0 = ϕ(t = 0) называется начальной фазой колебаний.
Слайд 8Дифференциальное уравнение гармонических колебаний
Найдем первую и вторую производные по времени
t от колеблющейся физической величины x:
Таким образом, эти величины совершают
гармонические колебания с той же частотой ω, но с амплитудами ωA и ω2A и со сдвигом по фазе на π/2 и π соответственно.
Слайд 9Дифференциальное уравнение гармонических колебаний
Как видно из приведенного уравнения, если физическая
величина x изменяется по закону гармонических колебаний, то она удовлетворяет
дифференциальному уравнению гармонических колебаний:
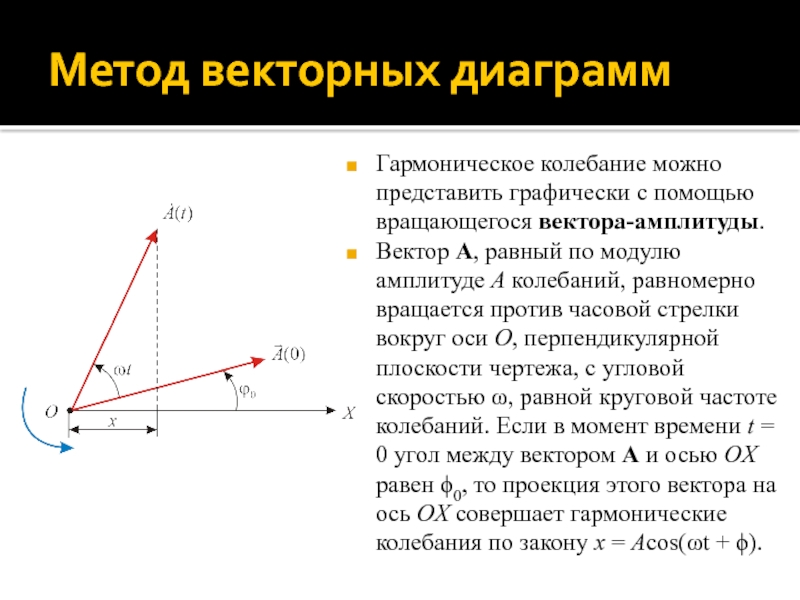
Слайд 10Метод векторных диаграмм
Гармоническое колебание можно представить графически с помощью вращающегося
вектора-амплитуды.
Вектор A, равный по модулю амплитуде A колебаний, равномерно вращается
против часовой стрелки вокруг оси O, перпендикулярной плоскости чертежа, с угловой скоростью ω, равной круговой частоте колебаний. Если в момент времени t = 0 угол между вектором A и осью OX равен ϕ0, то проекция этого вектора на ось OX совершает гармонические колебания по закону x = Acos(ωt + ϕ).
Слайд 111.2 Свободные незатухающие колебания. Маятники
ЛЕКЦИЯ 1. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ
Слайд 12Свободные механические колебания
Если смещение консервативной механической системы из положения устойчивого
равновесия описывается одним параметром x, то при малых x потенциальную
энергию можно разложить в ряд:
Потенциальную энергию колебательной системы принято отсчитывать от положения устойчивого равновесия, в котором Π(x = 0) = 0, (dΠ/dx)x=0 = 0 (в положении устойчивого равновесия потенциальная энергия имеет минимум).
Слайд 13Свободные механические колебания
Таким образом, при малых смещения из положения устойчивого
равновесия:
Система совершает гармонические колебания.
При этом величину –dΠ/dx = Fx называют
обобщенной силой, которая при малых x пропорциональна смещению: Fx = –κx.
Если x – координата, то обобщенная сила – проекция силы F на направление X; если x – угол отклонения ϕ, то обобщенная сила – вращательный момент M.
Слайд 14Квазиупругая сила
В этом случае уравнение движения тела имеет вид:
(такой же
вид, как и уравнение движения груза на пружине в отсутствие
сил трения и сопротивления). Поэтому в этом случае силу Fx = –κx называют квазиупругой, а коэффициент κ – эффективной жесткостью.
Если сравнить уравнение движения с уравнением гармонических колебаний
то видно, что циклическая частота и период колебаний соответственно равны ω = (κ/m)1/2 и T = 2π(m/κ)1/2.
Слайд 15Пружинный маятник
Рассмотрим спиральную пружину жесткостью k, один конец которой закреплен
неподвижно, а к другому прикреплено тело (материальная точка массы m),
которое может двигаться в горизонтальном направлении без трения или сопротивления.
Примем за начало координат положение тела, при котором пружина недеформирована
На тело действует сила упругости, направленная к положению равновесия. Таким образом, уравнение движения тела:
Слайд 16Пружинный маятник
Сравнивая это уравнение с дифференциальным уравнением гармонических колебаний,
находим, что
собственная циклическая частота ω и период T гармонических колебаний пружинного
маятника соответственно равны:
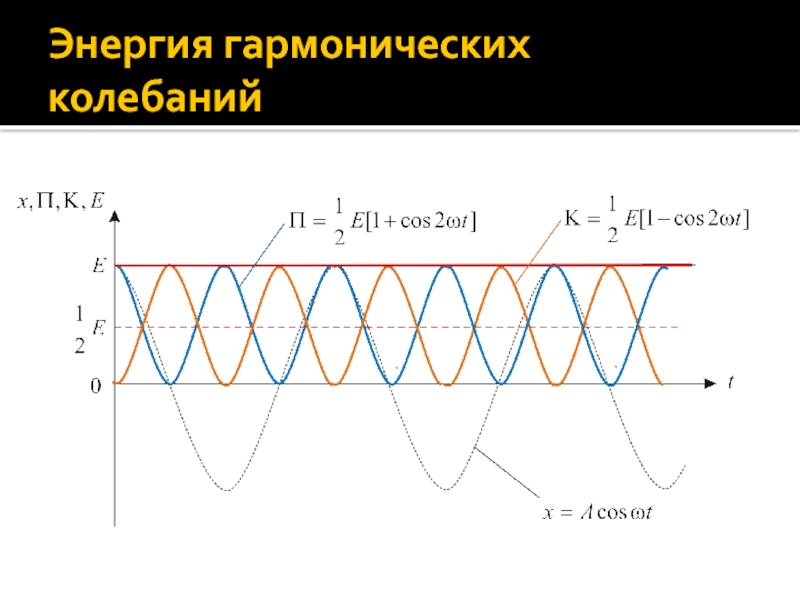
Слайд 17Энергия гармонических колебаний
Если точка совершает гармонические колебания по закону
x = Acos(ωt + ϕ0), то ее потенциальная
и кинетическая энергии изменяются также по гармоническому закону с частотой 2ω:
Здесь учтено, что ω = (κ/m)1/2 и
т.е. при гармонических колебаниях полная механическая энергия точки сохраняется.
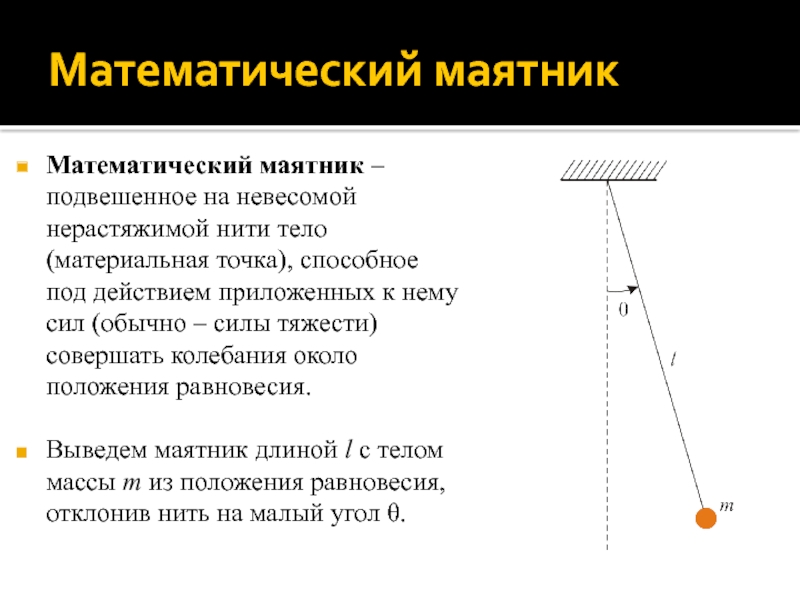
Слайд 19Математический маятник
Математический маятник – подвешенное на невесомой нерастяжимой нити тело
(материальная точка), способное под действием приложенных к нему сил (обычно
– силы тяжести) совершать колебания около положения равновесия.
Выведем маятник длиной l с телом массы m из положения равновесия, отклонив нить на малый угол θ.
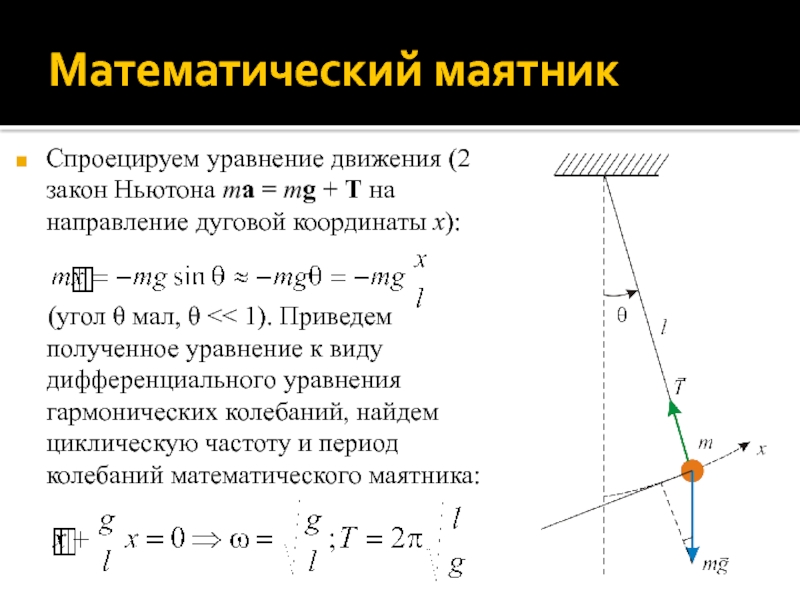
Слайд 20Математический маятник
Спроецируем уравнение движения (2 закон Ньютона ma = mg
+ T на направление дуговой координаты x):
(угол θ мал, θ
<< 1). Приведем полученное уравнение к виду дифференциального уравнения гармонических колебаний, найдем циклическую частоту и период колебаний математического маятника:
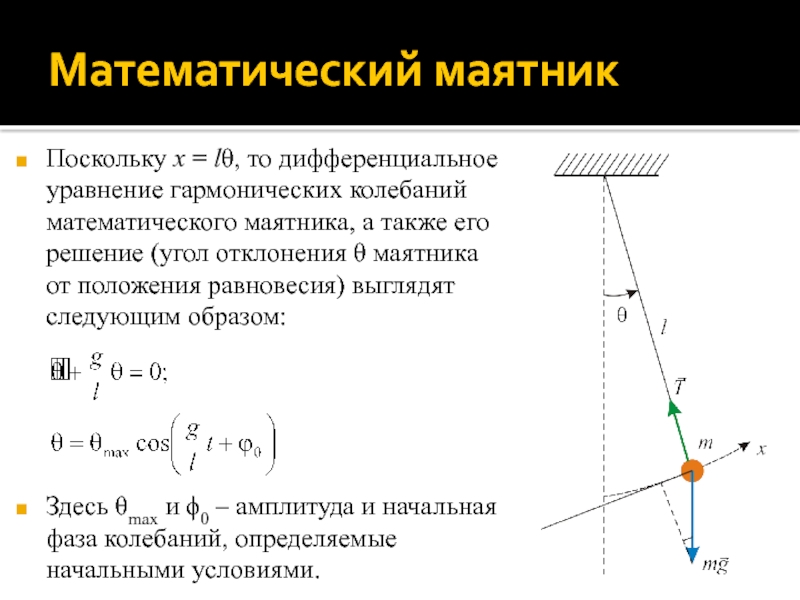
Слайд 21Математический маятник
Поскольку x = lθ, то дифференциальное уравнение гармонических колебаний
математического маятника, а также его решение (угол отклонения θ маятника
от положения равновесия) выглядят следующим образом:
Здесь θmax и ϕ0 – амплитуда и начальная фаза колебаний, определяемые начальными условиями.
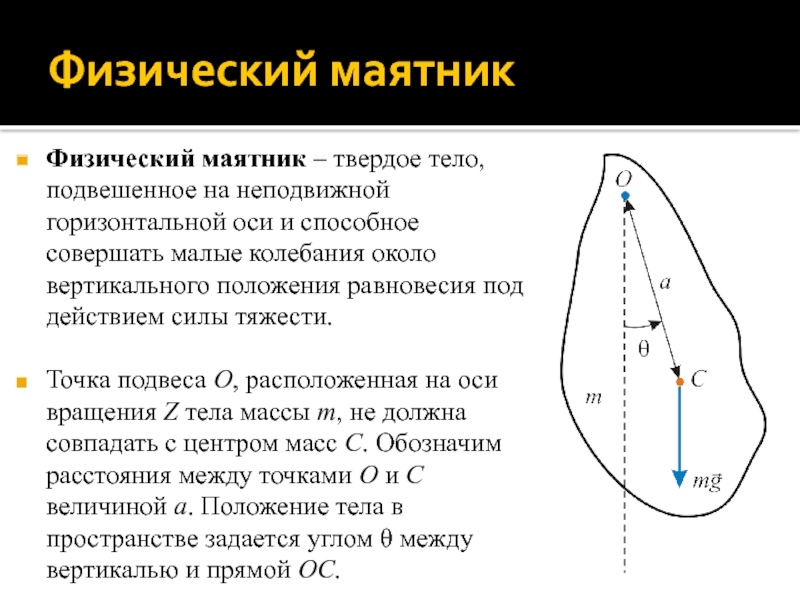
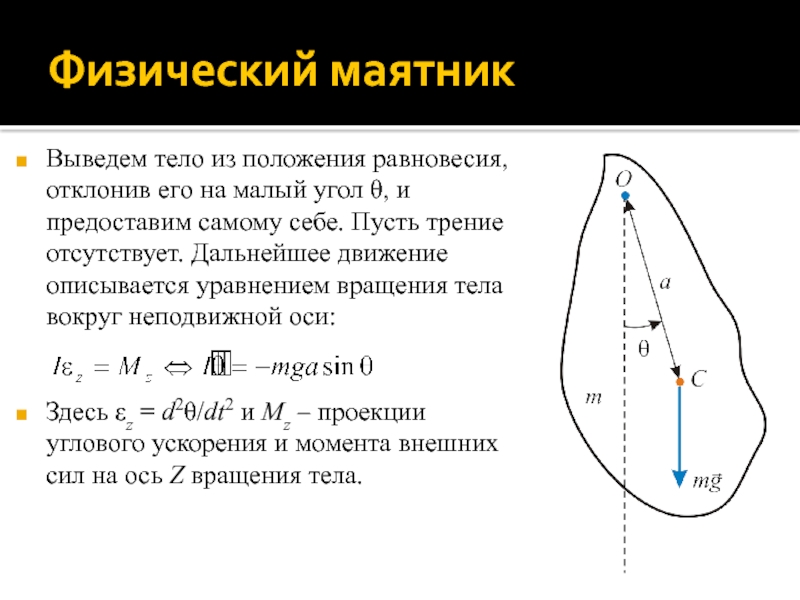
Слайд 22Физический маятник
Физический маятник – твердое тело, подвешенное на неподвижной горизонтальной
оси и способное совершать малые колебания около вертикального положения равновесия
под действием силы тяжести.
Точка подвеса O, расположенная на оси вращения Z тела массы m, не должна совпадать с центром масс C. Обозначим расстояния между точками O и C величиной a. Положение тела в пространстве задается углом θ между вертикалью и прямой OC.
Слайд 23Физический маятник
Выведем тело из положения равновесия, отклонив его на малый
угол θ, и предоставим самому себе. Пусть трение отсутствует. Дальнейшее
движение описывается уравнением вращения тела вокруг неподвижной оси:
Здесь εz = d2θ/dt2 и Mz – проекции углового ускорения и момента внешних сил на ось Z вращения тела.
Слайд 24Физический маятник
Момент силы реакции опоры (оси) N равен нулю, поскольку
равно нулю плечо этой силы.
Следовательно, Mz есть проекция на ось
Z силы тяжести:
(считаем, что угол отклонения маятника мал). Таким образом, получим дифференциальное уравнение гармонических колебаний физического маятника:
Слайд 25Физический маятник
Решение этого уравнения (угловая координата):
Здесь θmax и ϕ0 –
амплитуда и начальная фаза колебаний, определяемые начальными условиями.
Циклическая частота и
период колебаний физического маятника:
Слайд 26Приведенная длина
физического маятника
Приведенной длиной lпр физического маятника называется длина
такого математического маятника, период колебаний которого совпадает с периодом колебаний
данного физического маятника. Найдем ее.
Согласно определению,
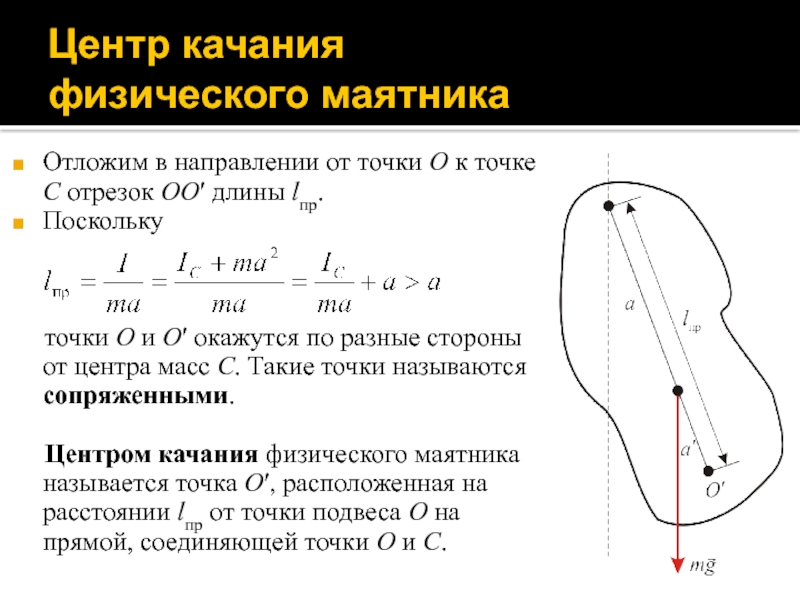
Слайд 27Центр качания
физического маятника
Отложим в направлении от точки O к
точке C отрезок OO′ длины lпр.
Поскольку
точки O и O′ окажутся
по разные стороны от центра масс C. Такие точки называются сопряженными.
Центром качания физического маятника называется точка O′, расположенная на расстоянии lпр от точки подвеса O на прямой, соединяющей точки O и C.
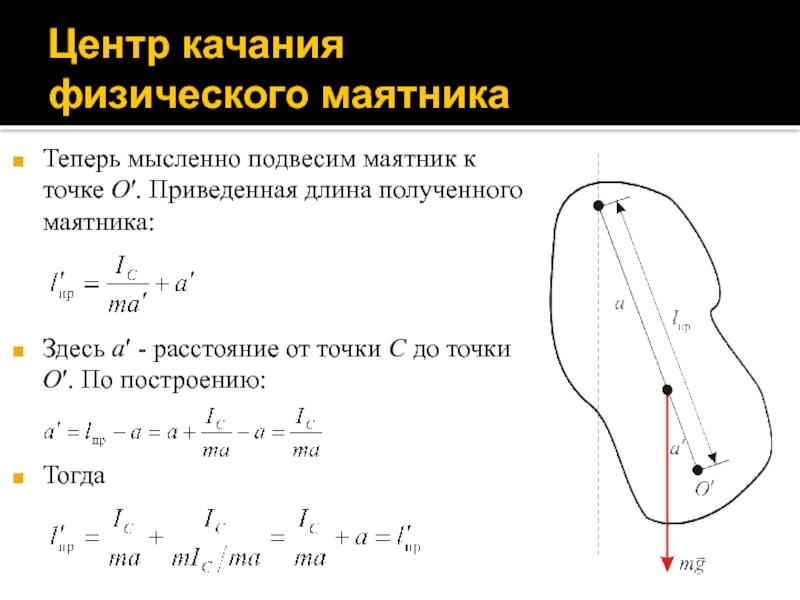
Слайд 28Центр качания
физического маятника
Теперь мысленно подвесим маятник к точке O′.
Приведенная длина полученного маятника:
Здесь a′ - расстояние от точки C
до точки O′. По построению:
Тогда
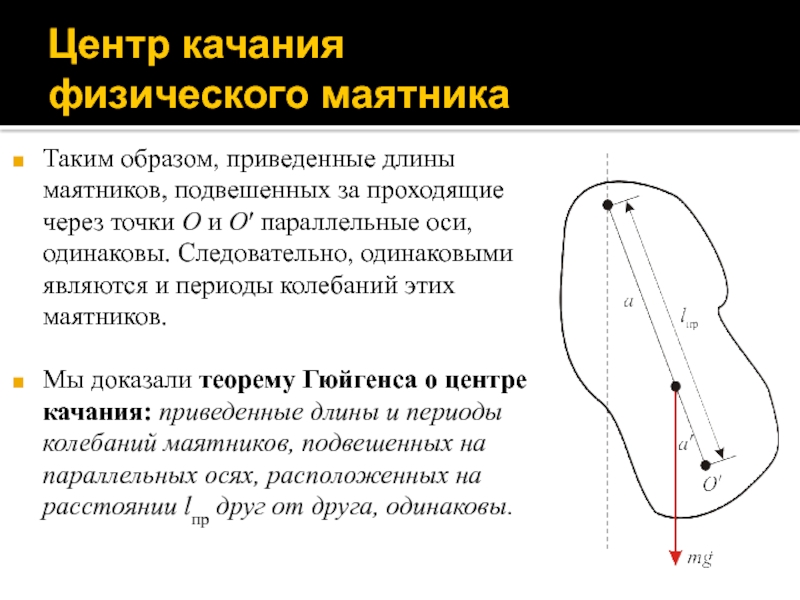
Слайд 29Центр качания
физического маятника
Таким образом, приведенные длины маятников, подвешенных за
проходящие через точки O и O′ параллельные оси, одинаковы. Следовательно,
одинаковыми являются и периоды колебаний этих маятников.
Мы доказали теорему Гюйгенса о центре качания: приведенные длины и периоды колебаний маятников, подвешенных на параллельных осях, расположенных на расстоянии lпр друг от друга, одинаковы.
Слайд 301.3 Сложение колебаний
ЛЕКЦИЯ 1. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ
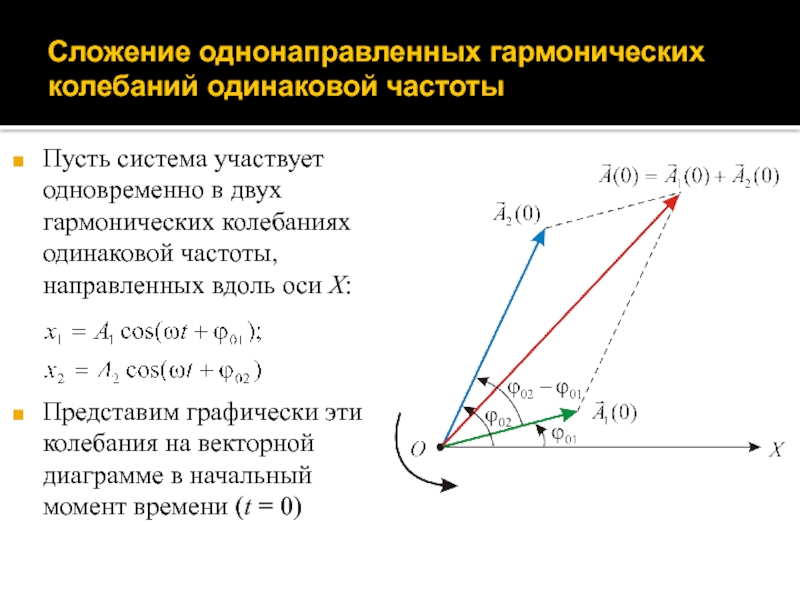
Слайд 31Сложение однонаправленных гармонических колебаний одинаковой частоты
Пусть система участвует одновременно в
двух гармонических колебаниях одинаковой частоты, направленных вдоль оси X:
Представим графически
эти колебания на векторной диаграмме в начальный момент времени (t = 0)
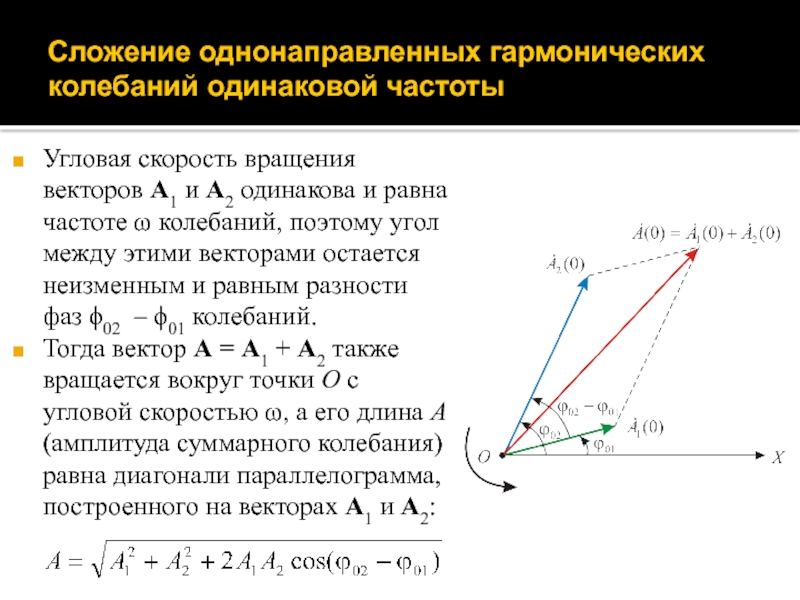
Слайд 32Сложение однонаправленных гармонических колебаний одинаковой частоты
Угловая скорость вращения векторов A1
и A2 одинакова и равна частоте ω колебаний, поэтому угол
между этими векторами остается неизменным и равным разности фаз ϕ02 – ϕ01 колебаний.
Тогда вектор A = A1 + A2 также вращается вокруг точки O с угловой скоростью ω, а его длина A (амплитуда суммарного колебания) равна диагонали параллелограмма, построенного на векторах A1 и A2:
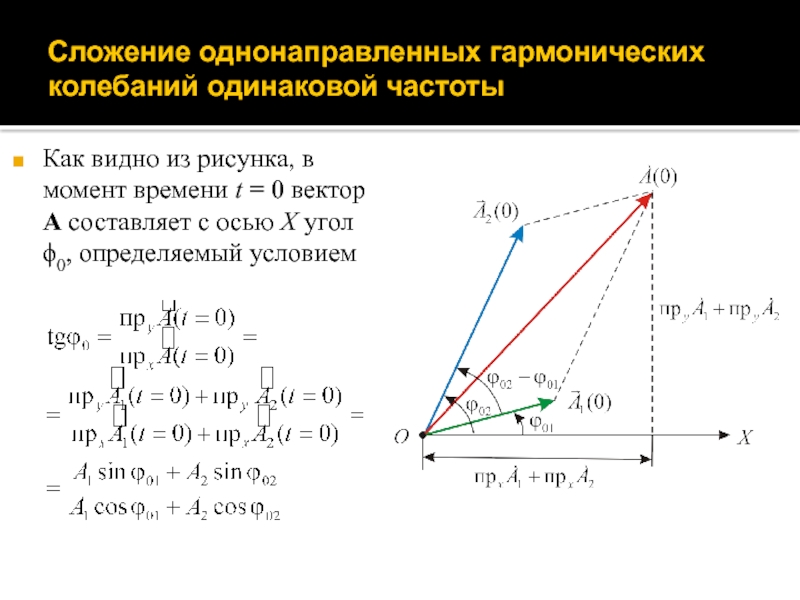
Слайд 33Сложение однонаправленных гармонических колебаний одинаковой частоты
Как видно из рисунка, в
момент времени t = 0 вектор A составляет с осью
X угол ϕ0, определяемый условием
Слайд 34Сложение однонаправленных гармонических колебаний одинаковой частоты
Таким образом, при сложении двух
однонаправленных гармонических колебаний
одинаковой частоты ω (такие колебания называются когерентными) получается
гармоническое колебание той же частоты, амплитуда A и начальная фаза ϕ0 которого определяются по приведенным выше формулам:
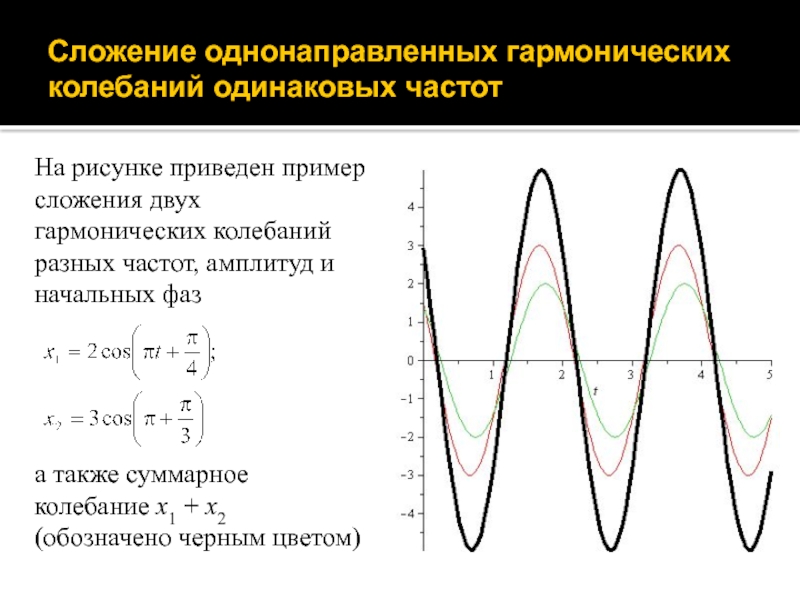
Слайд 35Сложение однонаправленных гармонических колебаний одинаковых частот
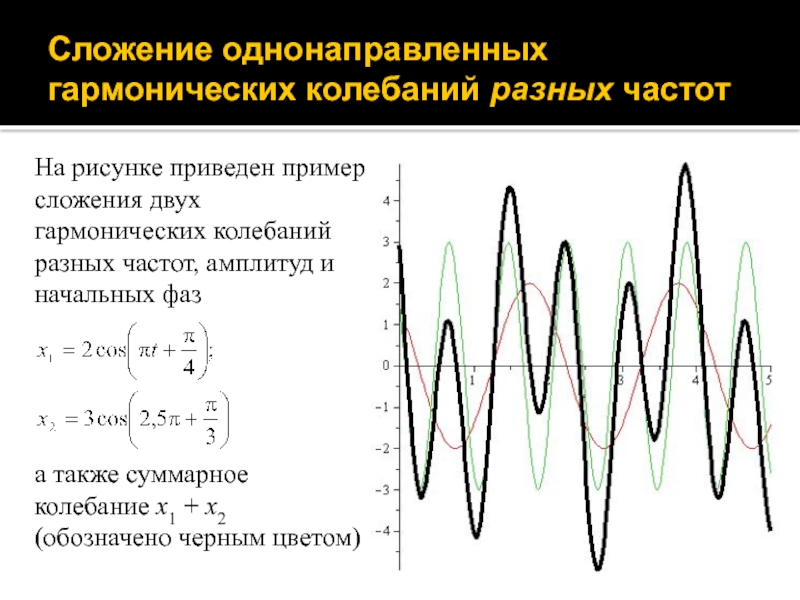
На рисунке приведен пример сложения
двух гармонических колебаний разных частот, амплитуд и начальных фаз
а также
суммарное колебание x1 + x2 (обозначено черным цветом)
Слайд 36Сложение однонаправленных гармонических колебаний разных частот
При сложении однонаправленных гармонических колебаний
с разными частотами
векторы A1 и A2 на векторной диаграмме
вращаются вокруг точки O с разными (ω1 и ω2) угловыми скоростями, поэтому вектор A = A1 + A2 деформируется со временем, т.е. движение системы не будет являться гармоническим колебанием.
Слайд 37Сложение однонаправленных гармонических колебаний разных частот
На рисунке приведен пример сложения
двух гармонических колебаний разных частот, амплитуд и начальных фаз
а также
суммарное колебание x1 + x2 (обозначено черным цветом)
Слайд 38Сложение однонаправленных гармонических колебаний разных частот
Однако при сложении колебаний с
близкими частотами
на промежутке времени τ = 2π/Δω колебания можно считать
когерентными. В результате сложения таких колебаний получается колебание, происходящее с частотой ω = (ω1 + ω2)/2, а их амплитуда A меняется от Amax = A1 + A2 до Amin = | A1 – A2 |. Такие колебания называют биениями, ωБ = Δω –частотой биений, а TБ = 2π/ωБ = 2π/Δω – периодом биений.
Слайд 39Сложение однонаправленных гармонических колебаний разных частот
Получим уравнение биений для частого
случая, когда A1 = A2 = A0:
Если при этом начальные
фазы колебаний одинаковы (ϕ01 = ϕ02 = ϕ0), то уравнение биений можно привести к виду:
Слайд 40Биения
Модуль первого множителя в формуле называется амплитудой биений. Это медленно
меняющаяся со временем величина:
Найдем период биений:
Слайд 42Биения
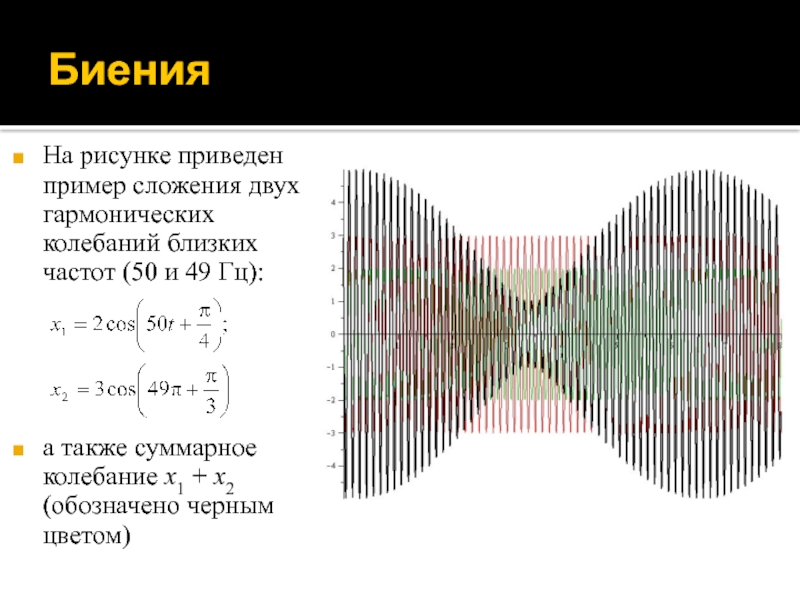
На рисунке приведен пример сложения двух гармонических колебаний близких частот
(50 и 49 Гц):
а также суммарное колебание x1 + x2
(обозначено черным цветом)
Слайд 43Биения
Биения представляют собой один из примеров модулированных колебаний, т.е. колебаний,
происходящих по закону гармонических колебаний, в котором один из параметров
периодически меняется со временем с периодом, значительно превышающим период основных колебаний.
Различают амплитудную, частотную и фазовую модуляции.
Слайд 44Сложение перпендикулярных гармонических колебаний
Если точка движется по плоскости таким образом,
что ее проекции на оси X и Y совершают гармонические
колебания, то говорят о сложении взаимно перпендикулярных гармонических колебаний.
Слайд 45Сложение перпендикулярных гармонических колебаний одинаковой частоты
При сложении колебаний одинаковой частоты
траекторией
точки в общем случае является наклонный эллипс:
Слайд 46Сложение перпендикулярных гармонических колебаний одинаковых частот
Такое движение точки называют эллиптически
поляризованными колебаниями. Движение может происходить по часовой стрелке (при 2mπ
< ϕ02 – ϕ01 < (2m+1)π или против часовой стрелки; в этих случаях говорят о правой или левой эллиптической поляризации.
Слайд 47Вывод уравнения траектории точки, совершающей два взаимно перпендикулярных колебания одинаковой
частоты
Выведем уравнение наклонного эллипса. Для этого преобразуем уравнения гармонических колебаний
вдоль осей X и Y:
Слайд 48Сложение перпендикулярных гармонических колебаний одинаковых частот
На рисунке изображена траектория точки,
совершающей два перпендикулярные гармонические колебания одинаковых частот:
Слайд 49Сложение перпендикулярных гармонических колебаний одинаковых частот
При ϕ02 – ϕ01 =
(2m + 1)π/2 оси эллипса совпадают с осями координат:
Слайд 50Сложение перпендикулярных гармонических колебаний одинаковых частот
На рисунке изображена траектория точки,
совершающей два перпендикулярные гармонические колебания одинаковых частот:
Слайд 51Сложение перпендикулярных гармонических колебаний одинаковых частот
При ϕ02 – ϕ01 =
mπ эллипс вырождается в прямую; такое движение называется линейно поляризованными
колебаниями:
Слайд 52Сложение перпендикулярных гармонических колебаний одинаковых частот
На рисунке изображена траектория точки,
совершающей два перпендикулярные гармонические колебания одинаковых частот:
Слайд 53Сложение перпендикулярных гармонических колебаний разных частот
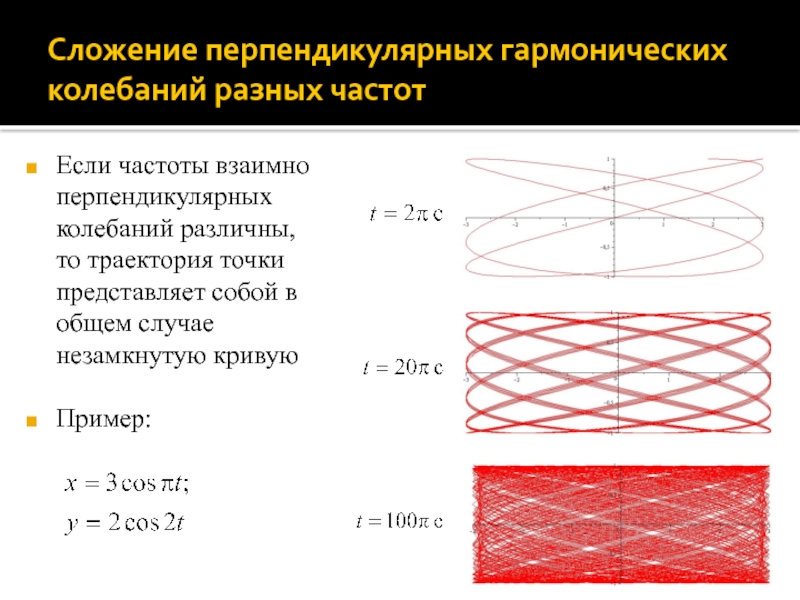
Если частоты взаимно перпендикулярных колебаний
различны, то траектория точки представляет собой в общем случае незамкнутую
кривую
Пример:
Слайд 54Фигуры Лиссажу
При сложении взаимно перпендикулярных колебаний с различными, но кратными
частотами результирующее колебание происходит по траекториям, называемым фигурами Лиссажу:
Вид фигуры
Лиссажу зависит от соотношения частот, от амплитуд и начальных фаз складываемых колебаний.
Слайд 55Фигуры Лиссажу
На рисунке изображена траектория точки, совершающей два перпендикулярные гармонические
колебания, частоты которых относятся как целые числа:
Слайд 56Фигуры Лиссажу
По виду фигуры Лиссажу можно судить о соотношении частот
складываемых взаимно перпендикулярных колебаний: отношение частот двух гармонических колебаний вдоль
осей X и Y обратно пропорционально отношению числа пересечений фигуры Лиссажу осей X и Y.
Слайд 571.4 Свободные затухающие колебания
ЛЕКЦИЯ 1. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ
Слайд 58Затухающие колебания
Во всякой колебательной системе есть силы трения и сопротивления
среды (диссипативные силы), в которой находится тело. Действие этих сил
приводит к уменьшению механической энергии тела. Если убыль энергии не восполняется за счет работы внешних сил, то колебания затухают. При этом механическая энергия превращается в теплоту.
Затухающими называются свободные колебания механической системы при наличии сил трения или сопротивления.
Получим уравнение затухающих колебаний на примере тела, колеблющегося в вязкой среде под действием упругой силы пружины.
Слайд 59Дифференциальное уравнение затухающих колебаний
Выведем тело из положения равновесия, растянув или
сжав пружину и предоставим систему самой себе.
На тело действуют: сила
упругости и сила сопротивления среды, направленная противоположно скорости тела: Fсопр = –rv, где r – коэффициент сопротивления среды.
Уравнение движения:
Слайд 60Дифференциальное уравнение затухающих колебаний
Обозначим:
Здесь β – коэффициент затухания, ω0 –
циклическая частота свободных незатухающих гармонических колебаний. Тогда дифференциальное уравнение свободных
затухающих колебаний примет вид:
Слайд 61Решение дифференциального уравнения затухающих колебаний
Если β < ω0, то решение
дифференциального уравнения затухающих колебаний имеет вид:
Здесь A(t) – амплитуда затухающих
колебаний, A0 – начальная амплитуда. В отличие от гармонических колебаний, амплитуда затухающих колебаний зависит от времени – уменьшается с течением времени по экспоненциальному закону.
ω – циклическая частота затухающих колебаний, которая не совпадает с циклической частотой ω0 гармонических колебаний (собственной частотой механической системы).
Слайд 62Решение дифференциального уравнения затухающих колебаний
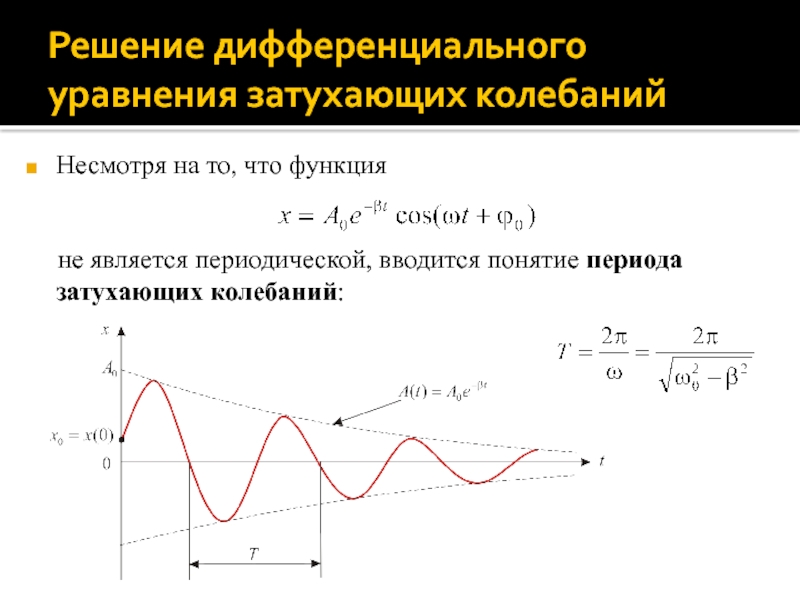
Несмотря на то, что функция
не является
периодической, вводится понятие периода затухающих колебаний:
Слайд 63Скорость тела при затухающих колебаниях
Скорость тела при затухающих колебаниях равна
Здесь
введен вспомогательный угол ϕ, для которого
Слайд 64Коэффициент затухания β
Здесь r – коэффициент сопротивления среды, m –
масса тела. Коэффициент затухания определяет, насколько быстро уменьшается амплитуда колебаний
с течением времени.
Коэффициент затухания численно равен обратному времени, за которое амплитуда колебаний уменьшается в e раз.
Величины, характеризующие затухание колебаний
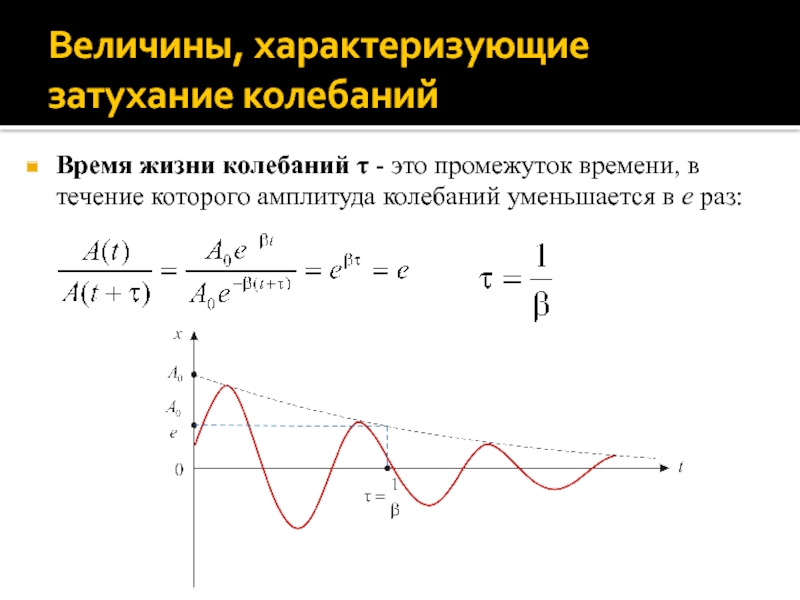
Слайд 65Время жизни колебаний τ - это промежуток времени, в течение
которого амплитуда колебаний уменьшается в e раз:
Величины, характеризующие затухание колебаний
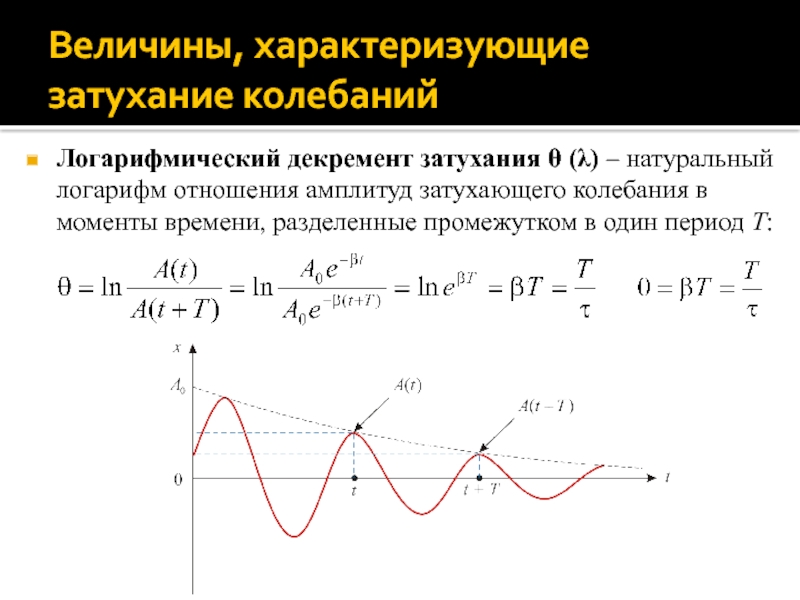
Слайд 66Логарифмический декремент затухания θ (λ) – натуральный логарифм отношения амплитуд
затухающего колебания в моменты времени, разделенные промежутком в один период
T:
Величины, характеризующие затухание колебаний
Слайд 67Добротность Q – умноженное на число π количество колебаний за
время, в течение которого амплитуда уменьшается в e раз:
При слабом
затухании (β << ω0) добротность Q равна (с точностью до коэффициента 2π) отношению энергии E колебаний к величине потерь энергии за один период |ΔE|:
Величины, характеризующие затухание колебаний
Слайд 68Поскольку энергия системы прямо пропорциональна квадрату амплитуды A колебаний, то
Продифференцируем
по времени выражение для энергии E и учтем малость затухания,
т.е. dE/dt ≈ΔE/ΔT:
Тогда
Физический смысл добротности
Примечание. Добротность колебательной системы дает грубую оценку числа периодов, в течение которых практически вся механическая энергия превращается в теплоту.
Слайд 69При увеличении коэффициента сопротивления среды r и, соответственно, коэффициента затухания
β период затухающих колебаний возрастает:
При β → ω0 T→ ∞,
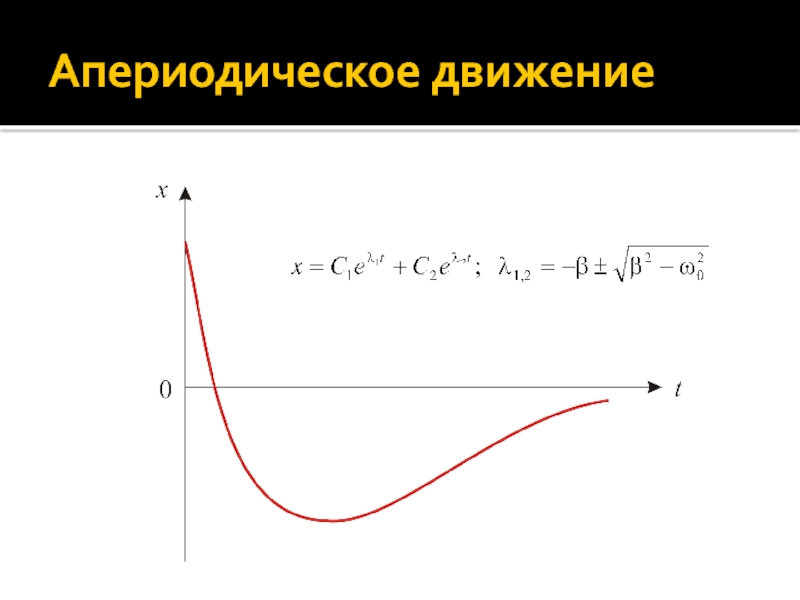
т.е. при достаточно большом коэффициента затухания β колебания в системе невозможны. При этом выведенная из положения система возвращается в это положение, не совершая колебаний. Такое движение, при котором отсутствует признак колебаний – повторяемость, – называется апериодическим движением.
Апериодическое движение
Слайд 70
Если коэффициент затухания β > ω0, то решение дифференциального уравнения
затухающих колебаний имеет вид:
Здесь C1,2 – постоянные коэффициенты, зависящие от
начальных условий движения. Поскольку параметры λ1,2 < 0, а функция x представляет собой сумму убывающих экспонент, величина x – отклонение системы от положения равновесия – быстро приближается к нулевому значению
Апериодическое движение
Слайд 72
Если выполнено условие β = ω0, то решение дифференциального уравнения
затухающих колебаний имеет вид:
Здесь C1,2 – постоянные коэффициенты, зависящие от
начальных условий движения. При выполнении условия β = ω0 поведение механической системы называется критическим режимом, а параметр β – критическим коэффициентом затухания.
Апериодическое движение
Слайд 731.5 Вынужденные колебания. Резонанс
ЛЕКЦИЯ 1. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ
Слайд 74Свободные колебания, возникающие под влиянием начального толчка, ввиду действия сил
трения и сопротивления, с течением времени затухают.
Для того, чтобы
в системе происходили незатухающие колебания, необходимо компенсировать потери энергии. Такая компенсация может производиться за счет внешних по отношению к колебательной системе источников энергии.
Рассмотрим простейший случай, когда на систему воздействует внешняя сила, изменяющаяся со временем по гармоническому закону:
Вынужденные колебания
Слайд 75Вынужденные колебания – колебания, возникающие в механической системе под действием
внешней периодической силы и происходящие с частотой изменения этой силы.
Если
внешняя сила описывается гармонической функцией с циклической частотой ω, то механическая система будет совершать вынужденные колебания в такт с внешней силой, т.е. на частоте ω
Получим дифференциальное уравнение вынужденных колебаний, воспользовавшись моделью пружинного маятника массы m, связанного пружиной жесткости k и движущегося в вязкой среде вдоль параллельной пружине оси X.
Вынужденные колебания
Слайд 76Дифференциальное уравнение вынужденных колебаний
На тело действуют: сила упругости Fупр =
–kr, сила сопротивления Fсопр = –rv и внешняя сила F
= Fcosωt, направленная вдоль оси X. Уравнение движения тела:
Получим уравнение вынужденных колебаний:
Слайд 77Дифференциальное уравнение вынужденных колебаний и его решение
Здесь β = r/2m
– коэффициент затухания, ω0 = (k/m)1/2 – собственная частота системы.
В теории линейных дифференциальных уравнений показывается, что решение этого уравнения имеет вид:
Первое слагаемое – решение уравнения затухающих колебаний – затухающее колебание с частотой ω′ = (ω02 - β2 ). Второе слагаемое – вынужденное колебание с частотой ω, равной частоте вынуждающей силы.
Слайд 78Дифференциальное уравнение вынужденных колебаний и его решение
Затухание колебаний имеет значительную
роль только на начальной стадии колебательного процесса. С течением времени
первое слагаемое (экспоненциальный спад) быстро уменьшается.
По прошествии достаточного времени t, определяемого из условия A0e–βt << A, затуханием колебаний (т.е. первым слагаемым) можно пренебречь.
Промежуток времени, по истечении которого можно пренебречь затухающими колебаниями называется временем установления колебаний.
Слайд 79Амплитуда и начальная фаза
затухающих колебаний
Определим амплитуду A, сдвиг фаз
ψ между смещением x и вынуждающей силой F в условиях,
когда решение уравнения вынужденных колебаний можно представить в виде
Продифференцируем это выражение по времени, найдя скорость и ускорение тела:
Слайд 80Амплитуда и начальная фаза
затухающих колебаний
Подставим величину x, ее первую
и вторую производные в дифференциальное уравнение вынужденных колебаний:
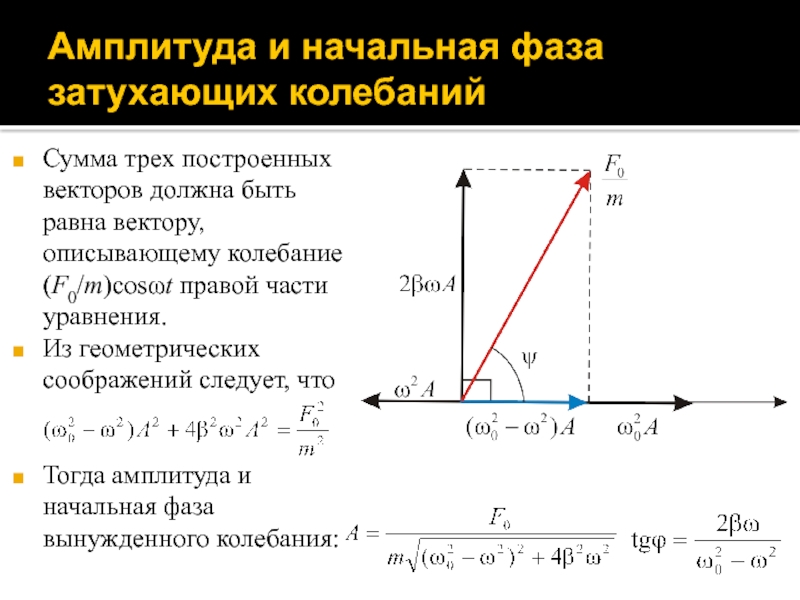
Теперь с помощью
метода векторной диаграммы найдем графически сумму трех гармонических колебаний одинаковой частоты ω в левой части полученного выражения.
Для этого представим:
колебание ω02Acos(ωt – ϕ) в виде вектора длиной ω02A;
колебание 2βAωcos(ωt – ϕ + π/2) в виде вектора длиной 2βAω, повернутого на угол π/2 против часовой стрелки относительно первого;
колебание ω2Acos(ωt – ϕ + π) в виде вектора длиной ω2A, повернутого на угол π относительного первого вектора.
Слайд 81Амплитуда и начальная фаза
затухающих колебаний
Сумма трех построенных векторов должна
быть равна вектору, описывающему колебание (F0/m)cosωt правой части уравнения.
Из геометрических
соображений следует, что
Тогда амплитуда и начальная фаза вынужденного колебания:
Слайд 82Резонанс
Всякая механическая колебательная система характеризуется собственной частотой ω0 и коэффициентом
затухания β. При заданных величинах ω0 и β амплитуда A
вынужденных колебаний механической системы зависит от частоты ω вынуждающей силы:
Резонанс – явление резкого возрастания амплитуды вынужденных колебаний до своего максимального значения при определенном значении частоты вынуждающей силы.
Соответствующая частота ω называется резонансной частотой.
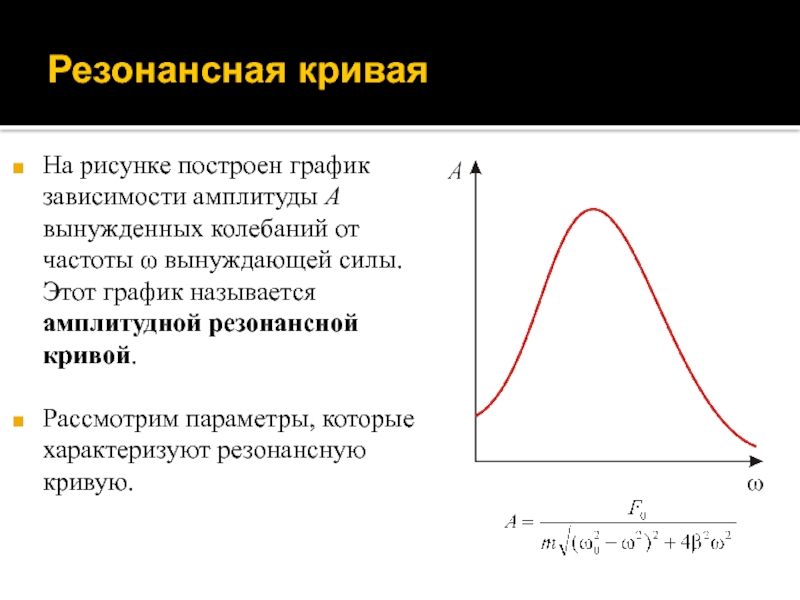
Слайд 83Резонансная кривая
На рисунке построен график зависимости амплитуды A вынужденных колебаний
от частоты ω вынуждающей силы. Этот график называется амплитудной резонансной
кривой.
Рассмотрим параметры, которые характеризуют резонансную кривую.
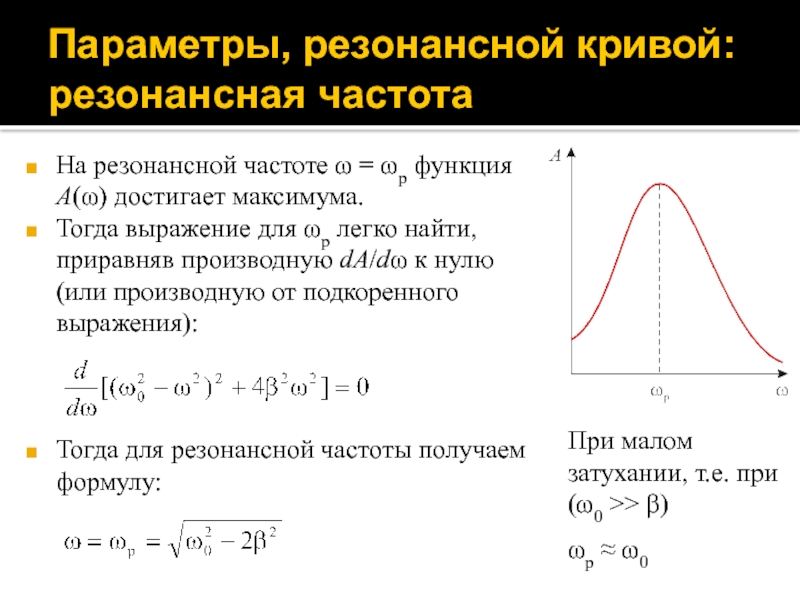
Слайд 84Параметры, резонансной кривой: резонансная частота
На резонансной частоте ω = ωр
функция A(ω) достигает максимума.
Тогда выражение для ωр легко найти,
приравняв производную dA/dω к нулю (или производную от подкоренного выражения):
Тогда для резонансной частоты получаем формулу:
При малом затухании, т.е. при (ω0 >> β)
ωр ≈ ω0
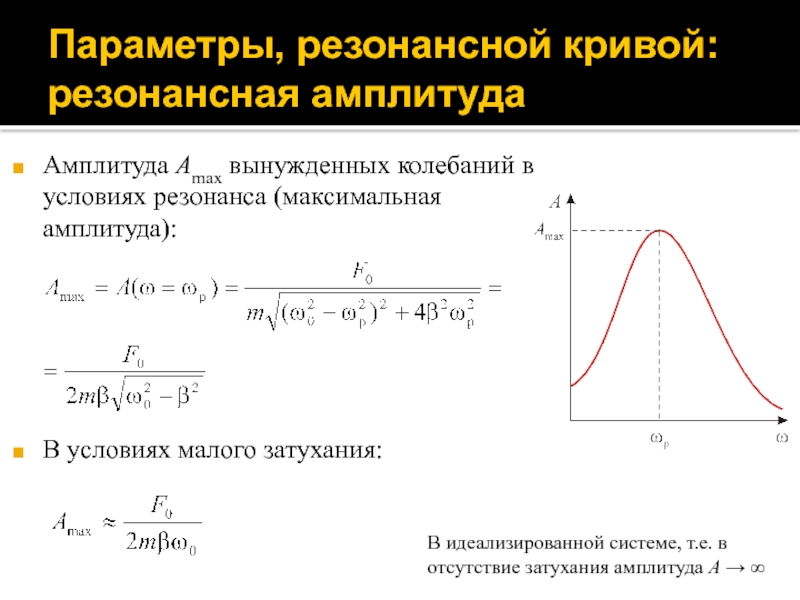
Слайд 85Параметры, резонансной кривой: резонансная амплитуда
Амплитуда Amax вынужденных колебаний в условиях
резонанса (максимальная амплитуда):
В условиях малого затухания:
В идеализированной системе, т.е. в
отсутствие затухания амплитуда A → ∞
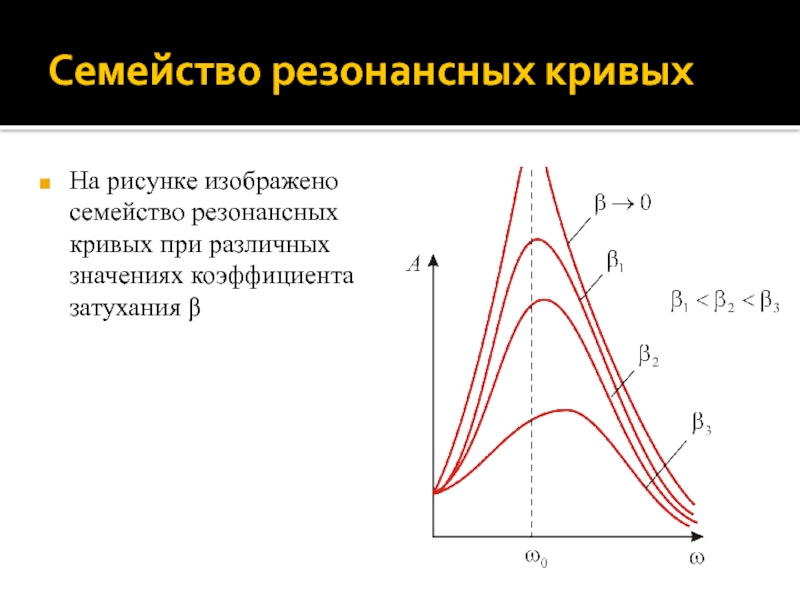
Слайд 86Семейство резонансных кривых
На рисунке изображено семейство резонансных кривых при различных
значениях коэффициента затухания β
Слайд 87Параметры, резонансной кривой: амплитуда при ω → 0
Стремление ω →
0 означает, что внешняя сила F = F0cos(ωt) с течением
времени изменяется очень медленно, т.е. ее можно считать постоянной величиной F ≈ F0.
В этих условиях тело смещается из положения равновесия и его координата x мало меняется со временем.
Слайд 88Параметры, резонансной кривой: амплитуда при ω → 0
Амплитуда вынужденного колебания
равна величине смещения тела из положения равновесия:
Если системой является пружинный
маятник, то ω0 = (k/m)1/2, тогда A0 = F0/k, т.е. амплитуда вынужденного колебания совпадает с удлинением пружины под действием постоянной силы.