Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
МИНИМИЗАЦИЯ БУЛЕВЫХ ФУНКЦИЙ. МЕТОД ГРАФ-СХЕМ
Содержание
- 1. МИНИМИЗАЦИЯ БУЛЕВЫХ ФУНКЦИЙ. МЕТОД ГРАФ-СХЕМ
- 2. Цель лекции – изучить метод граф-схем для
- 3. Литература Савельев А.Я. Прикладная теория цифровых автоматов.
- 4. Базовые понятия: Булева переменнаяБулева функцияДвоичная система счисленияДНФМинимальная форма функцииСущественная переменнаяТерминыКлючевые слова: Минимизация Минимальная ДНФ Неполностью определенная функция
- 5. Основные положения. 1Метод граф-схем предназначен для минимизация
- 6. Основные положения. 2В графическом виде разложение по
- 7. Основные положения. 3Граф схема функции регулярна, если
- 8. Time-Out
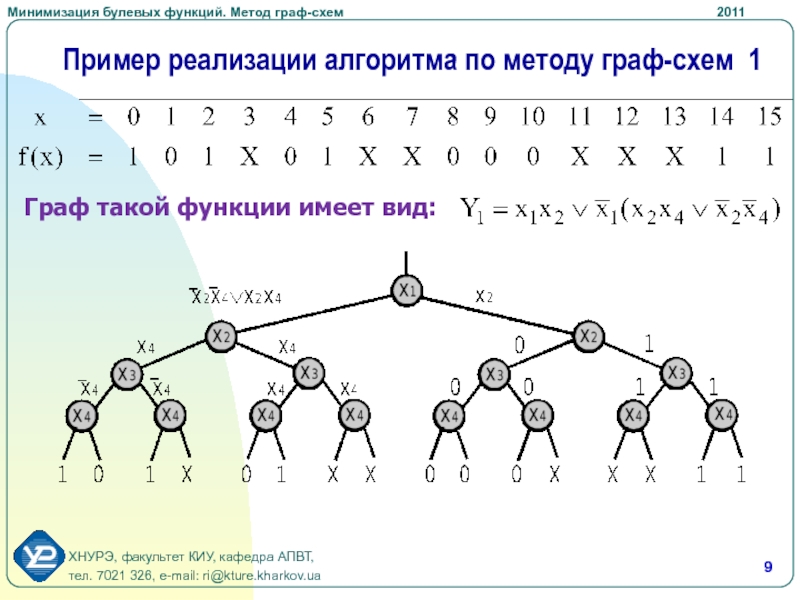
- 9. Пример реализации алгоритма по методу граф-схем 1Граф такой функции имеет вид:
- 10. Пример реализации алгоритма по методу граф-схем 2Входы
- 11. Пример реализации алгоритма по методу граф-схем 3При
- 12. Пример реализации алгоритма по методу граф-схем 4В
- 13. Пример реализации алгоритма по методу граф-схем 5Проверка
- 14. Алгоритм упорядочивания переменных в ярусах графа
- 15. Алгоритм упорядочивания переменных в ярусах графа
- 16. Алгоритм упорядочивания переменных в ярусах графа
- 17. ВыводыМетоды минимизации булевых функций используются во всех
- 18. Скачать презентанцию
Цель лекции – изучить метод граф-схем для минимизации булевых функций, описывающих комбинационные схемы цифровых проектов Содержание: Основные положения Алгоритм нахождения неопределенных коэффициентов Пример реализации алгоритмаТема: Минимизация булевых функций.
Слайды и текст этой презентации
Слайд 1МИНИМИЗАЦИЯ БУЛЕВЫХ ФУНКЦИЙ. МЕТОД ГРАФ-СХЕМ
ЛЕКЦИЯ 17
В.И. ХАХАНОВ
Факультет компьютерной инженерии и
управления, кафедра АПВТ, ХНУРЭ
Слайд 2Цель лекции – изучить метод граф-схем для минимизации булевых функций,
описывающих комбинационные схемы цифровых проектов
Содержание:
Основные положения
Алгоритм
нахождения неопределенных коэффициентовПример реализации алгоритма
Тема: Минимизация булевых функций.
Метод граф-схем
Слайд 3Литература
Савельев А.Я. Прикладная теория цифровых автоматов. М.: Высш. шк.,
1987. С. 194.
Хаханов В.І., Хаханова І.В., Кулак Е.М., Чумаченко
С.В. Методичні вказівки до практичних занять з курсу “Дискретна математика”. Харків, ХНУРЕ. 2001. С.35-43.Слайд 4Базовые понятия:
Булева переменная
Булева функция
Двоичная система
счисления
ДНФ
Минимальная форма функции
Существенная переменная
Термины
Ключевые слова:
Минимизация
Минимальная ДНФ
Неполностью определенная функция
Слайд 5Основные положения. 1
Метод граф-схем предназначен для минимизация неполностью определенных функций
Основывается
на теореме разложения функции по переменной xi
xi - компонент функции
есть- компонент функции есть
Переменная xi существенна, если
или
Слайд 6Основные положения. 2
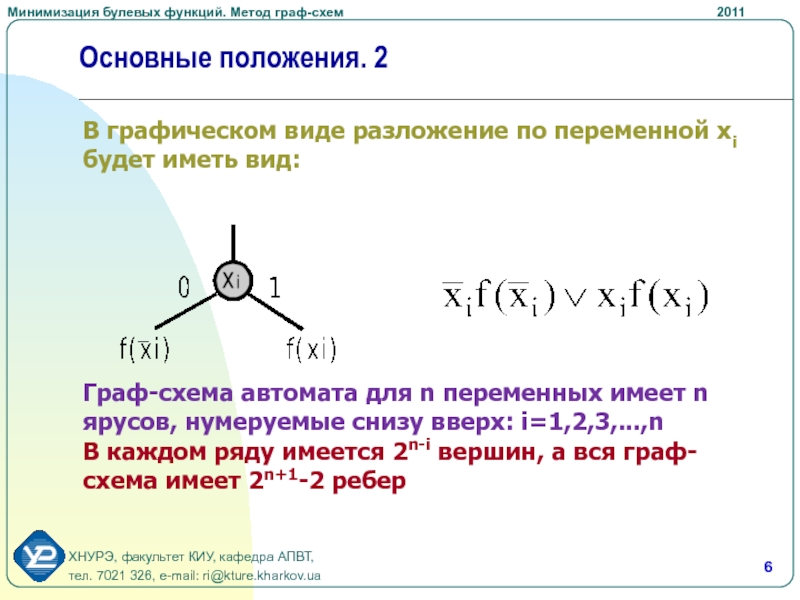
В графическом виде разложение по переменной xi будет
иметь вид:
Граф-схема автомата для n переменных имеет n ярусов, нумеруемые
снизу вверх: i=1,2,3,...,nВ каждом ряду имеется 2n-i вершин, а вся граф-схема имеет 2n+1-2 ребер
Слайд 7Основные положения. 3
Граф схема функции регулярна, если внутри каждого ряда
узлы имеют одинаковые аргументы.
Число всех возможных путей от входов
первого ряда к основанию равно 2n (n – число переменных). Входами для вершин нижнего ряда являются значения функции: f(x)={0,1,X}.
Слайд 10Пример реализации алгоритма по методу граф-схем 2
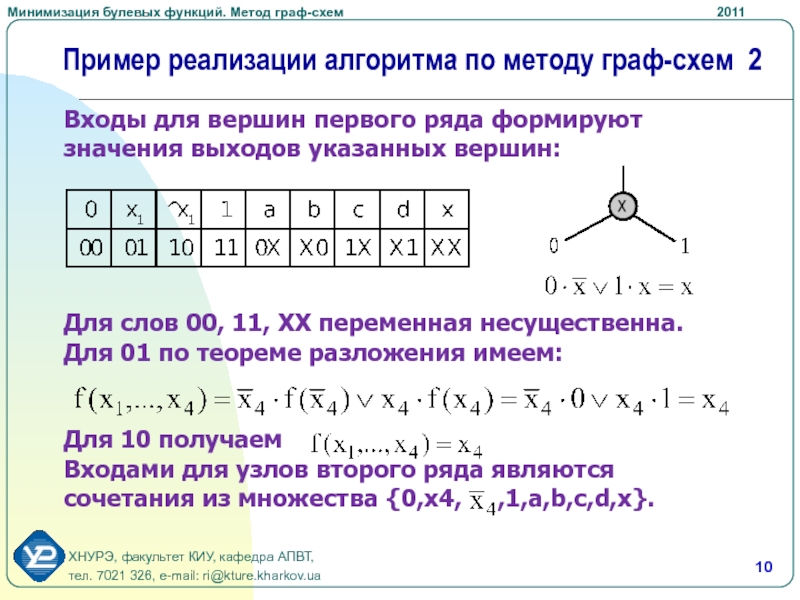
Входы для вершин первого
ряда формируют значения выходов указанных вершин:
Для слов 00, 11, ХХ
переменная несущественна.Для 01 по теореме разложения имеем:
Для 10 получаем
Входами для узлов второго ряда являются сочетания из множества {0,x4, ,1,a,b,c,d,x}.
Слайд 11Пример реализации алгоритма по методу граф-схем 3
При доопределении в нижнем
ярусе входов x символами {0} получим скобочную форму:
Первый вариант
для Y1 содержит 7 букв, второй – 9. Следовательно, чем больше в графе фиктивных переменных, тем проще конечный вид скобочной формы.Пути увеличения фиктивности переменных:
1. Оптимальное доопределение значений функций на неопределенных координатах нижнего яруса;
2. Перестановка переменных в ярусах графа.
Слайд 12Пример реализации алгоритма по методу граф-схем 4
В соответствии с правилом
2 предложим следующую перестановку переменных в ярусах:
В результате получается ГСА,
которая дает функцию из 6 букв, что свидетельствует о большей минимальности по сравнению с полученными ранее.
Слайд 13Пример реализации алгоритма по методу граф-схем 5
Проверка минимальности функции по
карте Карно дает следующий результат, идентичный полученному ранее:
Слайд 14Алгоритм упорядочивания переменных в ярусах графа
1
Общее число всех возможных вариантов граф-схем равно Q=n!2p, где n
– число переменных, р– количество неопределенных значений функции. Для рассматриваемого примера Q=4!.26=1536.
Определение. Сходность графа - есть оценка Q, где ki – число сходных узлов в i-м ярусе, где обе выходные функции одинаковы.
Сходность имеет пределы:
При этом S=0, если нет ни одного сходного узла
и если функция тождественно равна 0
или 1.
Если ki=2n-i для i-того яруса, то xi – фиктивная переменная.
На первом рисунке
На втором рисунке
Слайд 15Алгоритм упорядочивания переменных в ярусах графа
2
Для определения сходных узлов зададим операцию сравнения, где 0, 1,
Х, Y – значения булевых переменных или функций:Слайд 16Алгоритм упорядочивания переменных в ярусах графа
3
Процедура минимизации:
1. Вычисляется сходность для каждого яруса с последующей расстановкой
переменных по ярусам.2. Выполняется доопределение вхоных значений для нижнего яруса.
3. Выполняется запись скобочной формы по ГС.
Алгоритм определения ГС с максимальной сходимостью:
1. Определение xi для 1-го яруса: ;
2. Вычисление xi для 2-го яруса: ;
3. Определение xi для j-го яруса: .
Для подсчета сходности в ярусах используется таблица Венна, где наборы расположены по возрастанию их номеров.
Слайд 17Выводы
Методы минимизации булевых функций используются во всех программных приложениях, связанных
с синтезом вычислительных устройств
Они позволяют в среднем на 20-30% получить
более экономичный проект с позиции аппаратурных затратВысокий уровень структуризации представления булевой функции дает возможность минимизировать затраты при обработке схем с большим числом переменных
Метод граф-схем позволяет визуализировать процессы синтеза минимальных форм
Недостатком метода является значительный объем информации при хранении древовидной стуктуры представления булевой функции
Метод может быть использован при синтезе минимальногокубического покрытия