МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное

высшего профессионального образования «Московский государственный машиностроительный университет (МАМИ)» /УНИВЕРСИТЕТ МАШИНОСТРОЕНИЯ/ Факультет «Технологического

предпринимательства» Кафедра «Стандартизация, метрология и сертификация»

Докладчик : Орлова Алена Александровна
Группа: 154-341
преподаватель : Сергей Леонидович Петухов

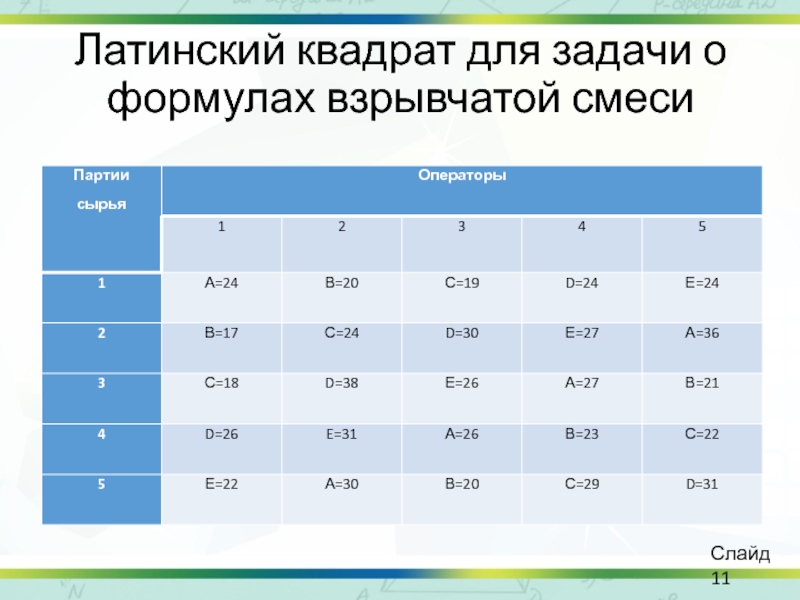
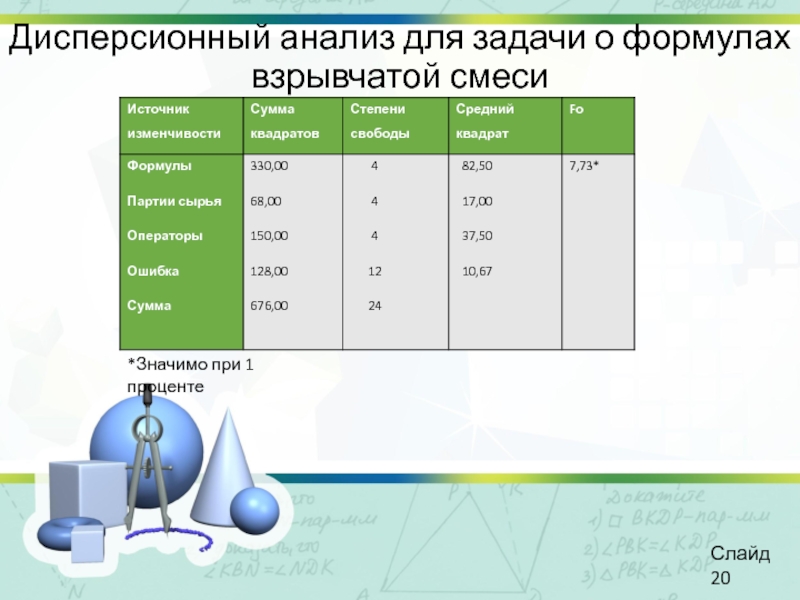
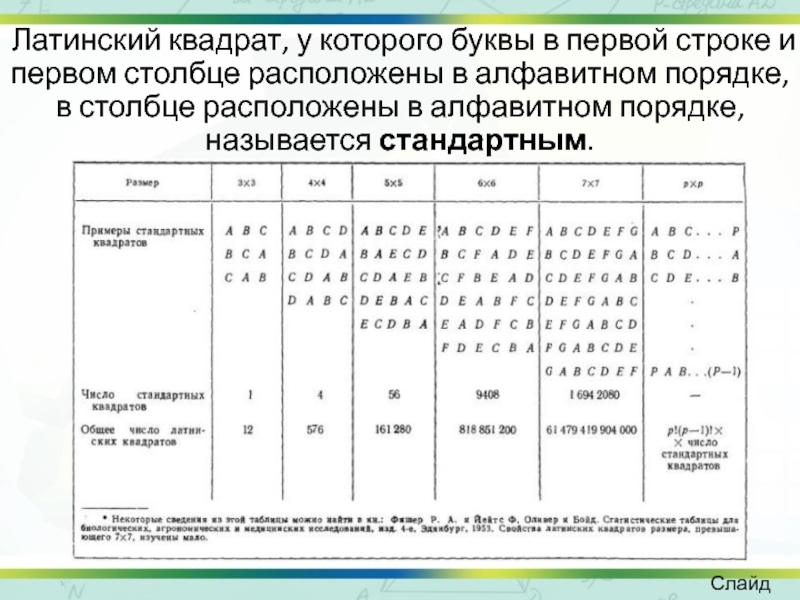
Доклад на тему: «дисперсионный анализ для латинского квадрата»

в экспериментальных данных путём исследования значимости различий в средних значениях.
Применяется для исследования

влияния одной или нескольких качественных переменных на одну зависимую количественную переменную. В основе дисперсионного анализа лежит предположение, что одни переменные могут рассматриваться как причины (независимые переменные), а другие как следствия (зависимые переменные или отклики).

Слайд 2

сравнения дисперсий. Дисперсию измеряемого признака разлагают на независимые слагаемые, каждое

из которых характеризует влияние того или иного фактора или их взаимодействия. Последующее сравнение таких слагаемых позволяет оценить значимость каждого изучаемого фактора, а также их комбинации.

Слайд 3

на одну зависимую количественную переменную. В основе дисперсионного анализа лежит

предположение, что одни переменные могут рассматриваться как причины (независимые переменные), а другие как следствия (зависимые переменные или отклики).

Слайд 4

заполненная n элементами множества М таким образом, что в каждой

строке и в каждом столбце таблицы каждый элемент из М встречается в точности один раз.

Слайд 5

особенностью: если один квадрат наложить на другой, то все пары получившихся

чисел оказываются различными. Такие пары латинских квадратов называются ортогональными

Слайд 6

в такой занимательной формулировке: “ Среди 36 офицеров поровну уланов,

драгунов, гусаров, кирасиров, кавалергардов и гренадеров и кроме того поровну генералов, полковников, майоров, капитанов, поручиков и подпоручиков, причем каждый род войск представлен офицерами всех шести рангов. Можно ли выстроить всех офицеров в каре 6 х 6 так, чтобы в любой колонне и любой шеренге встречались офицеры всех рангов?”

Слайд 7

было доказано, что такого решения не существует. В то же

время Эйлер доказал, что ортогональные пары латинских квадратов существуют для всех нечетных значений n и для таких четных значений n, которые делятся на 4. Эйлер выдвинул гипотезу, что для остальных значений n, то есть если число n при делении на 4 даст в остатке 2, ортогональных квадратов не существует. В 1901 г. было доказано, что ортогональных квадратов 6 6 не существует, и это усиливало уверенность в справедливости гипотезы Эйлера. Однако в 1959 г. помощью ЭВМ были найдены сначала ортогональные квадраты 10х10, потом 14х14, 18х18, 22х22. А затем было показано, что для любого n , кроме 6, существуют ортогональные квадраты nхn.

Слайд 8

экспериментах в сельском хозяйстве, физике, химии, технике.

Существует ряд игр, в

которых используются латинские квадраты. Наиболее известна из них судоку. В ней требуется частичный квадрат дополнить до латинского квадрата 9-го порядка, обладающего дополнительным свойством: все девять его подквадратов содержат по одному разу все натуральные числа от 1 до 9.

Слайд 9

различных формул взрывчатой смеси, используемых при производстве динамита, на наблюдаемую

силу взрыва. Смесь по каждой из формул приготавливается из партии сырья, объем которой позволяет проверить не более пяти формул. Далее смеси приготавливаются несколькими операторами, которые могут существенно различаться по квалификации и опыту. Таким образом, оказывается, что план эксперимента должен предусмотреть «усреднение» влияния двух внешних факторов – партий сырья и операторов.

Слайд 10

внешних источника неоднородности, т.е. чтобы обеспечить систематическое группирование в блоки

по двум направлениям.

4*4

5*5

6*6

Слайд 12

ɑi + τj + ßk + εijk,
i=1,2,…, p ; j=1,2,…,p;

; k=1,2,…,p;
Где yijk - наблюдение в i-й строке и k-м столбце для j-й обработки;
μ – математическое ожидание общего среднего;
ɑi – эффект i-й строки ;
τj - эффект j-й обработки;
ßk - эффект k-го столбца;
εijk - случайная ошибка.

Слайд 13

аддитивна, т.е. взаимодействия между строками, столбцами и обработками отсутствуют. Поскольку

на каждую ячейку приходится только одно наблюдение, то для его обозначения необходимы лишь два из трех индексов i, j и k.

Слайд 14

партии сырья, так и операторы представляют собой ограничения на рандомизацию.

В этом эксперименте используется латинский квадрат 5*5. После кодирования (вычитаем 25 из каждого наблюдения) мы получаем следующие данные.

Слайд 17

и операторов (столбцов) находятся следующим образом:

Суммы по обработкам (латинским буквам)

приведены ниже:

Слайд 18

проценте
Слайд 20

столбце расположены в алфавитном порядке, в столбце расположены в алфавитном

порядке, называется стандартным.

Слайд 21

элементами множества М таким образом, что в каждой строке и

в каждом столбце таблицы каждый элемент из М встречается в точности один раз.
Латинские квадраты применяются для того, чтобы исключить два внешних источника неоднородности, т.е. чтобы обеспечить систематическое группирование в блоки по двум направлениям.

Слайд 22