Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
МКОУ Погорельская СОШ Кощеев М.М
Содержание
- 1. МКОУ Погорельская СОШ Кощеев М.М
- 2. Результат тестаВерно: 14Ошибки: 0Отметка: 5Время: 0 мин. 38 сек.ещёисправить
- 3. Вариант 1в) Скрещивающиесяб) Параллельныеа) Пересекающиеся1. Точки А,
- 4. Вариант 12. Какое утверждение о прямых верное?б)
- 5. Вариант 1в) не пересекаются и лежат в
- 6. Вариант 1а) Если а//b, b//с то а//cб)
- 7. Вариант 1а) скрещиваютсяб) пересекаются5. Точка F не
- 8. Вариант 16. Прямая а параллельна плоскости α.
- 9. Вариант 1в) Прямые, параллельные одной плоскости, параллельны.б)
- 10. Вариант 18. Средняя линия MN трапеции АВСD
- 11. Вариант 19. Точка М не лежит на
- 12. Вариант 1а) 4б) 810. Прямая АВ пересекает
- 13. Вариант 1б) 7,5а) 9 11. Дан треугольник
- 14. Вариант 1б) 14а) 12 12. На сторонах
- 15. Вариант 1в) 12а) 15 13. Через концы
- 16. Вариант 1б) 5а) 4 14. Плоскость параллельная
- 17. Вариант 2б) Пересекающиесяа) Параллельныев) Скрещивающиеся1. Прямые АВ и ВС…..
- 18. Вариант 2в) Скрещивающиесяа) Параллельныеб) Пересекающиеся2. Нельзя провести плоскости через две прямые, если они……
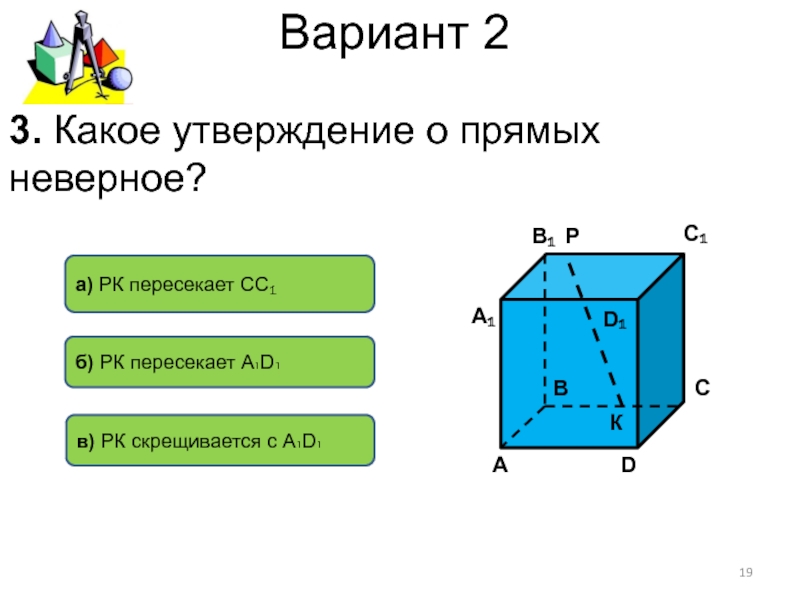
- 19. Вариант 23. Какое утверждение о прямых неверное?б)
- 20. Вариант 2б) скрещиваютсяа) пересекаются4. Точка D не
- 21. Вариант 2б) Две прямые, параллельные третьей прямой
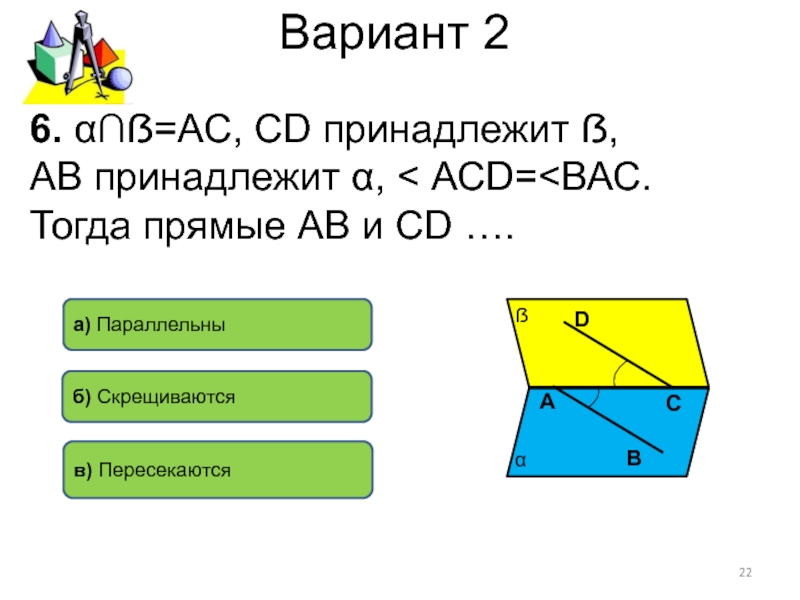
- 22. Вариант 26. α∩ẞ=АС, СD принадлежит ẞ, АВ принадлежит α, < АСD=
- 23. Вариант 2в) Если две прямые параллельны данной
- 24. Вариант 28. Точки М и N соответственно
- 25. Вариант 2б) Если прямая параллельна плоскости, то
- 26. Вариант 2а) 2б) 410. Прямая АВ пересекает
- 27. Вариант 2б) 10,5а) 21 11. Дан треугольник
- 28. Вариант 2б) 10а) 12 12. На сторонах
- 29. Вариант 2в) 8а) 11 13. Через концы
- 30. Вариант 1б) 8а) 16 14. Плоскость параллельная
- 31. Ключи к тесту: Взаимное расположение прямых в
- 32. Скачать презентанцию
Результат тестаВерно: 14Ошибки: 0Отметка: 5Время: 0 мин. 38 сек.ещёисправить
Слайды и текст этой презентации
Слайд 1Вариант 1
Вариант 2
Использован шаблон создания тестов в PowerPoint
МКОУ «Погорельская СОШ»
Кощеев
М.М.
Слайд 3Вариант 1
в) Скрещивающиеся
б) Параллельные
а) Пересекающиеся
1. Точки А, В, С и
D не лежат в одной плоскости. Тогда прямые АВ и
СD….
Слайд 4Вариант 1
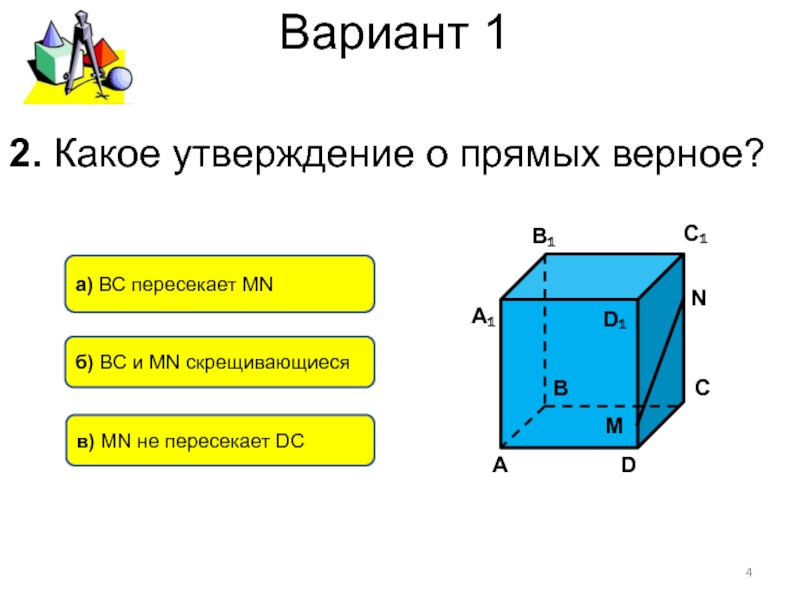
2. Какое утверждение о прямых верное?
б) ВС и MN
скрещивающиеся
а) ВС пересекает MN
в) MN не пересекает DC
А₁
А
В
С
D
В₁
С₁
D₁
М
N
Слайд 5Вариант 1
в) не пересекаются и лежат в одной плоскости
а) не
пересекаются
б) перпендикулярны некоторой прямой
3. Для доказательства параллельности
двух прямых
достаточно утверждать, что они …..
Слайд 6Вариант 1
а) Если а//b, b//с то а//c
б) Если а//b, а,
с – скрещивающиеся то с и b -скрещивающиеся
в) Если
а и b- скрещиваются, b и c- скрещиваются то а//с 4. Какое утверждение верное?
Слайд 7Вариант 1
а) скрещиваются
б) пересекаются
5. Точка F не лежит в плоскости
параллелограмма АВСD, N- середина DF, N- середина ВF. Тогда прямые
АМ и CN …….в) параллельны
Слайд 8Вариант 1
6. Прямая а параллельна плоскости α.
Тогда неверно, что
…..
а) Прямая а параллельна любой прямой, лежащей в плоскости α
б) Прямая а не пересекает ни одну прямую, лежащую в плоскости α
в) Существует прямая, лежащая в плоскости α, параллельная прямой а
Слайд 9Вариант 1
в) Прямые, параллельные одной плоскости, параллельны.
б) Если прямая параллельна
двум пересекающимся плоскостям, то она параллельна их линии пересечения
а) Если
плоскость проходит через данную прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой.7. Какое утверждение неверное?
Слайд 10Вариант 1
8. Средняя линия MN трапеции АВСD с
основаниями ВС
и АD лежит в плоскости
α. Вершина А не принадлежит данной
плоскости. Тогда прямая ВС…..
в) параллельна плоскости α
б) пересекает плоскость α
а) лежит в плоскости α
Слайд 11Вариант 1
9. Точка М не лежит на прямой а. Тогда
неверно, что через точку М можно
провести….
а) Только одну
прямую, не пересекающую прямую аб) Только одну прямую, параллельную прямой а
в) Бесконечно много прямых, не пересекающих прямую а.
Слайд 12Вариант 1
а) 4
б) 8
10. Прямая АВ пересекает плоскость α в
точке О. О – середина отрезка АВ. Расстояние от точки
А до плоскости α равно 4. Тогда расстояние от точки В до плоскости α равно…..в) 6
Слайд 13Вариант 1
б)
7,5
а)
9
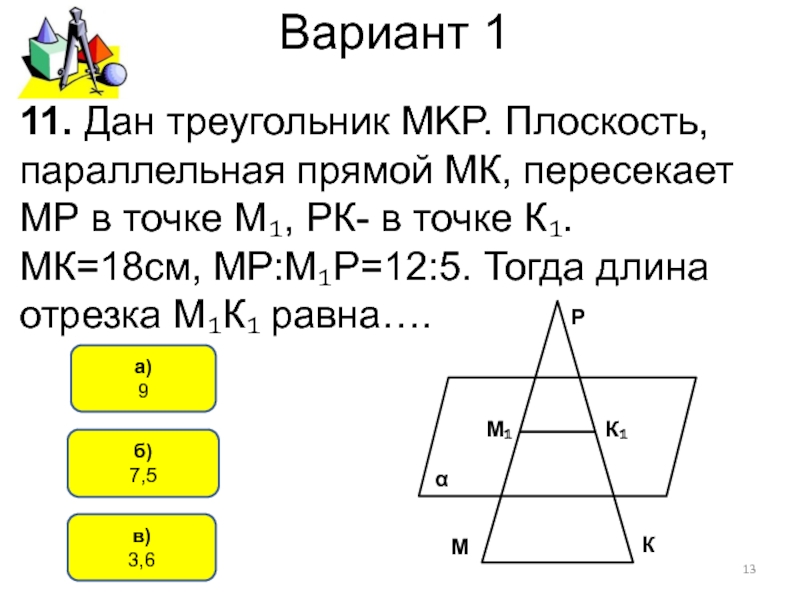
11. Дан треугольник MKP. Плоскость, параллельная
прямой МК, пересекает МР в точке М₁, РК- в точке
К₁. МК=18см, МР:М₁Р=12:5. Тогда длина отрезка М₁К₁ равна….
в)
3,6
α
Р
М₁
К₁
М
К
Слайд 14Вариант 1
б)
14
а)
12
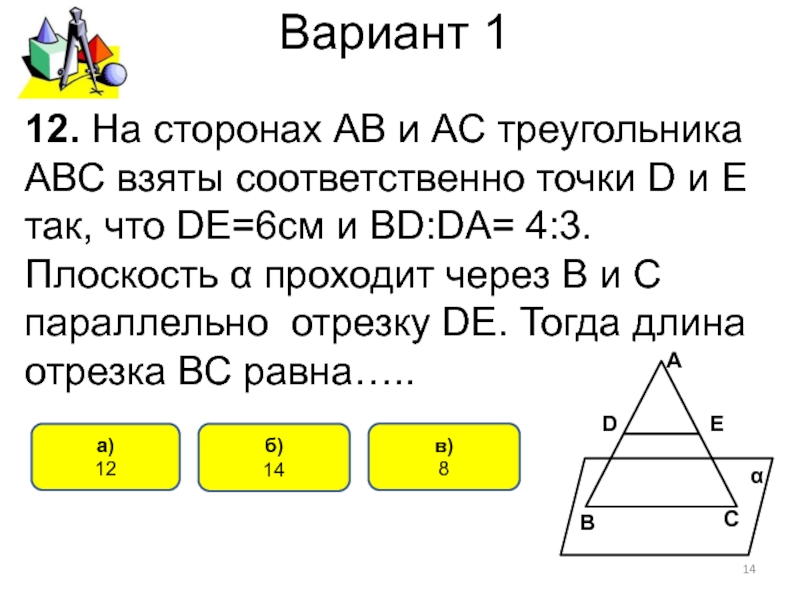
12. На сторонах АВ и АС
треугольника АВС взяты соответственно точки D и E так, что
DE=6см и ВD:DA= 4:3. Плоскость α проходит через В и С параллельно отрезку DE. Тогда длина отрезка ВС равна…..
в)
8
α
А
D
Е
В
С
Слайд 15Вариант 1
в)
12
а)
15
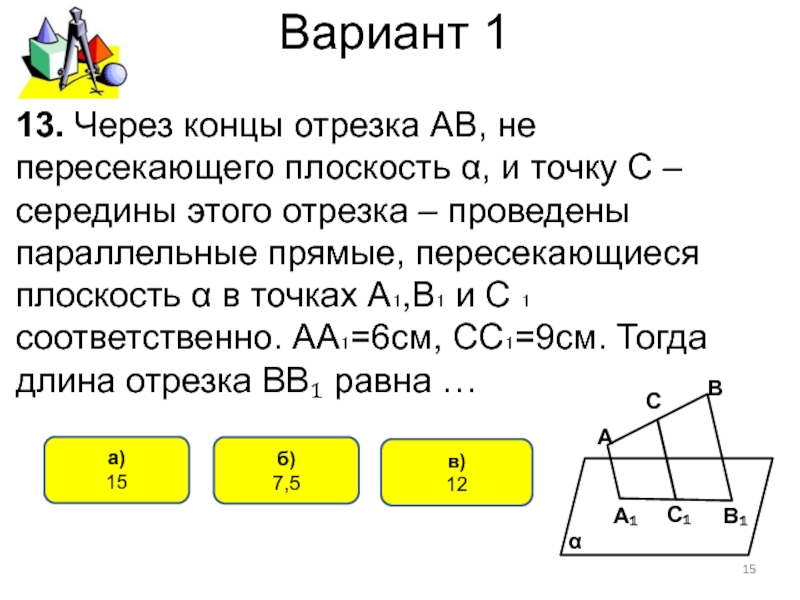
13. Через концы отрезка АВ, не
пересекающего плоскость α, и точку С – середины этого отрезка
– проведены параллельные прямые, пересекающиеся плоскость α в точках А₁,В₁ и С ₁ соответственно. АА₁=6см, СС₁=9см. Тогда длина отрезка ВВ₁ равна …
б)
7,5
А₁
В₁
С₁
α
А
С
В
Слайд 16Вариант 1
б)
5
а)
4
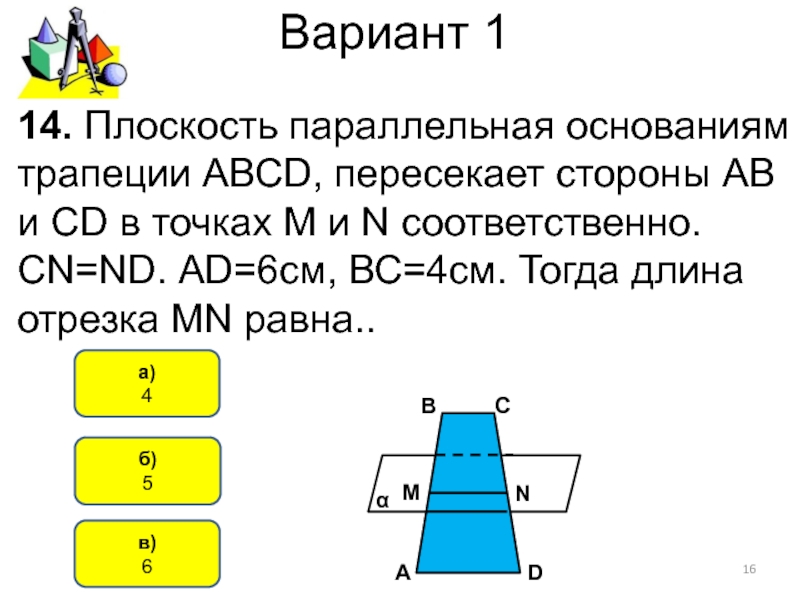
14. Плоскость параллельная основаниям трапеции АВСD,
пересекает стороны АВ и СD в точках M и N
соответственно. СN=ND. АD=6см, ВС=4см. Тогда длина отрезка MN равна..
в)
6
М
D
N
α
А
С
В
Слайд 18Вариант 2
в) Скрещивающиеся
а) Параллельные
б) Пересекающиеся
2. Нельзя провести плоскости через две
прямые, если они……
Слайд 19Вариант 2
3. Какое утверждение о прямых
неверное?
б) РК пересекает А₁D₁
а)
РК пересекает СС₁
в) РК скрещивается с А₁D₁
А₁
А
В
С
D
В₁
С₁
D₁
К
Р
Слайд 20Вариант 2
б) скрещиваются
а) пересекаются
4. Точка D не лежит в плоскости
треугольника АВС, К- середина DС. Тогда прямые АD и ВК
…….в) параллельны
Слайд 21Вариант 2
б) Две прямые, параллельные третьей прямой параллельны.
а) Две прямые
называются параллельными, если они не имеют общих точек.
в) Две прямые,
перпендикулярные третьей прямой, параллельны5. Какое утверждение верное?
Слайд 23Вариант 2
в) Если две прямые параллельны данной плоскости, то они
параллельны.
б) Если одна из двух параллельных прямых параллельна данной плоскости,
то и другая прямая параллельна данной плоскости или лежит в ней.а) Если одна из двух параллельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость.
7. Какое утверждение неверное?
Слайд 24Вариант 2
8. Точки М и N соответственно середины
сторон АВ
и ВС треугольника АВС.
Прямая MN лежит в плоскости α
. Точка В не принадлежит данной плоскости.
Тогда прямая АС……
в) параллельна плоскости α
б) пересекает плоскость α
а) лежит в плоскости α
Слайд 25Вариант 2
б) Если прямая параллельна плоскости, то она параллельна любой
прямой, лежащей в этой плоскости.
в) Если прямая параллельна плоскости, то
она не пересекает ни одну прямую, лежащую в этой плоскости.а) Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна данной плоскости.
9. Какое утверждение неверное?
Слайд 26Вариант 2
а) 2
б) 4
10. Прямая АВ пересекает плоскость α в
точке О. В – середина отрезка АО. Расстояние от точки
А до плоскости α равно 4. Тогда расстояние от точки В до плоскости α равно…..в) 6
Слайд 27Вариант 2
б) 10,5
а) 21
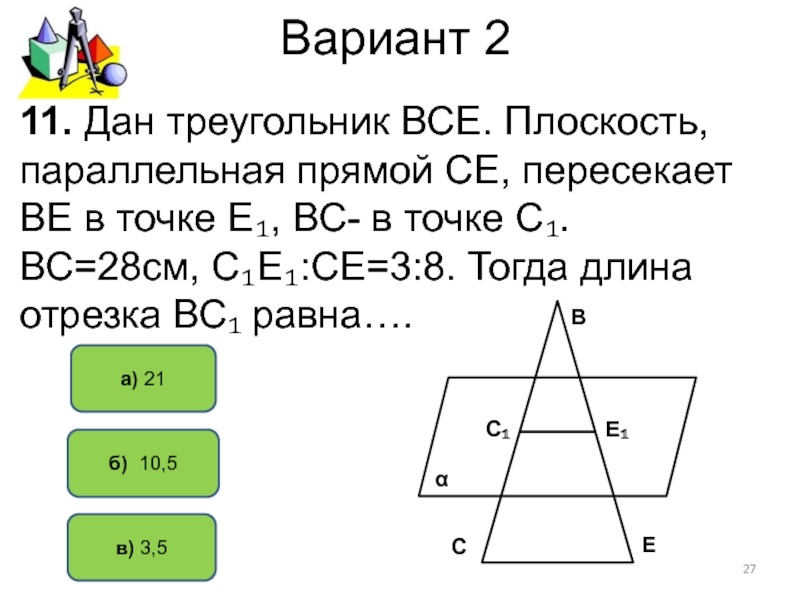
11. Дан треугольник ВСЕ. Плоскость, параллельная
прямой СЕ, пересекает ВЕ в точке Е₁, ВС- в точке
С₁. ВС=28см, С₁Е₁:СЕ=3:8. Тогда длина отрезка ВС₁ равна….
в) 3,5
α
В
С₁
Е₁
С
Е
Слайд 28Вариант 2
б)
10
а)
12
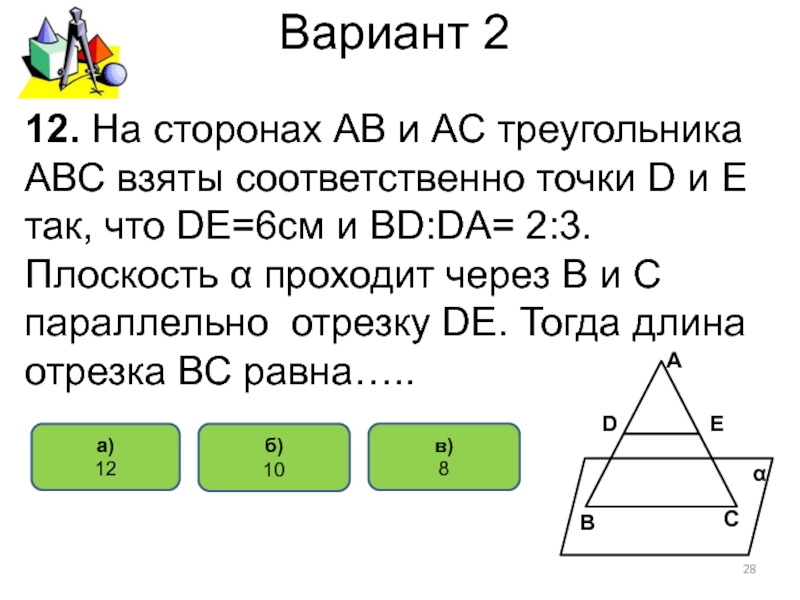
12. На сторонах АВ и АС
треугольника АВС взяты соответственно точки D и E так, что
DE=6см и ВD:DA= 2:3. Плоскость α проходит через В и С параллельно отрезку DE. Тогда длина отрезка ВС равна…..
в)
8
α
А
D
Е
В
С
Слайд 29Вариант 2
в)
8
а)
11
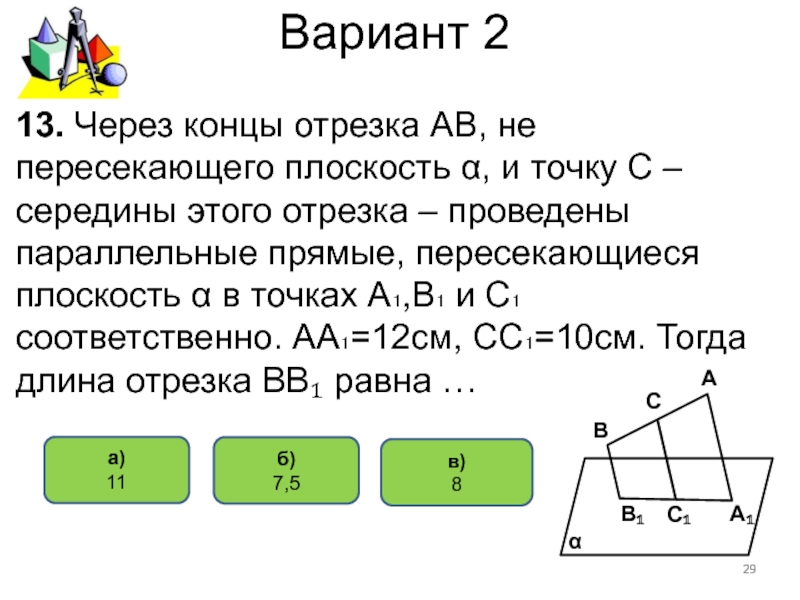
13. Через концы отрезка АВ, не
пересекающего плоскость α, и точку С – середины этого отрезка
– проведены параллельные прямые, пересекающиеся плоскость α в точках А₁,В₁ и С₁ соответственно. АА₁=12см, СС₁=10см. Тогда длина отрезка ВВ₁ равна …
б)
7,5
А₁
В₁
С₁
α
А
С
В
Слайд 30Вариант 1
б)
8
а)
16
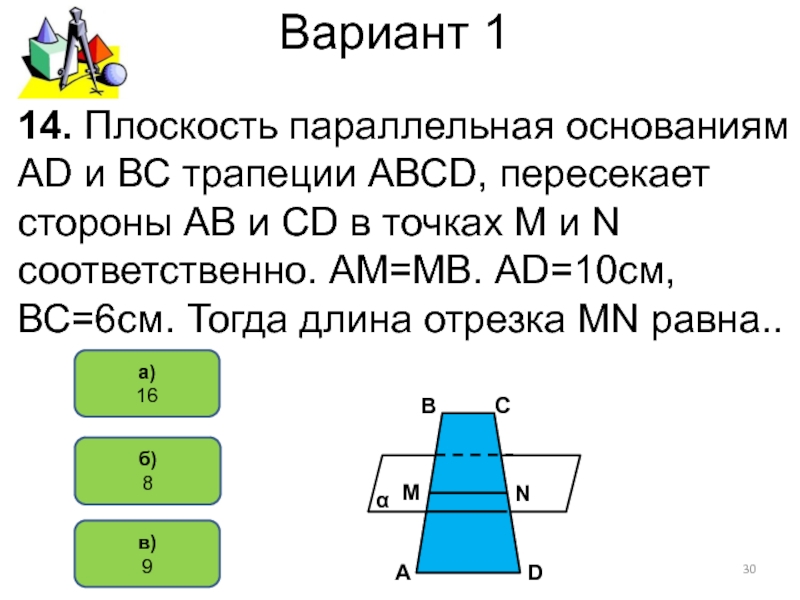
14. Плоскость параллельная основаниям AD и
ВС трапеции АВСD, пересекает стороны АВ и СD в точках
M и N соответственно. АМ=МВ. АD=10см, ВС=6см. Тогда длина отрезка MN равна..
в)
9
М
D
N
α
А
С
В
Слайд 31Ключи к тесту: Взаимное расположение прямых в пространстве.
Параллельность прямых,
прямой и плоскости.
Литература
Г.И. Ковалева, Н.И. Мазурова Геометрия 10-11 классы. Тесты
для текущего и обобщающего контроля. Изд-во «Учитель», 2009г.
