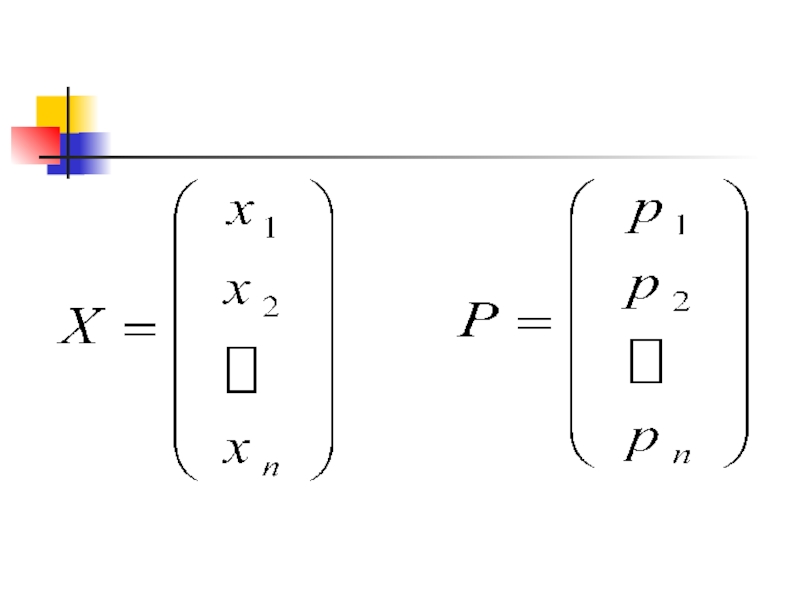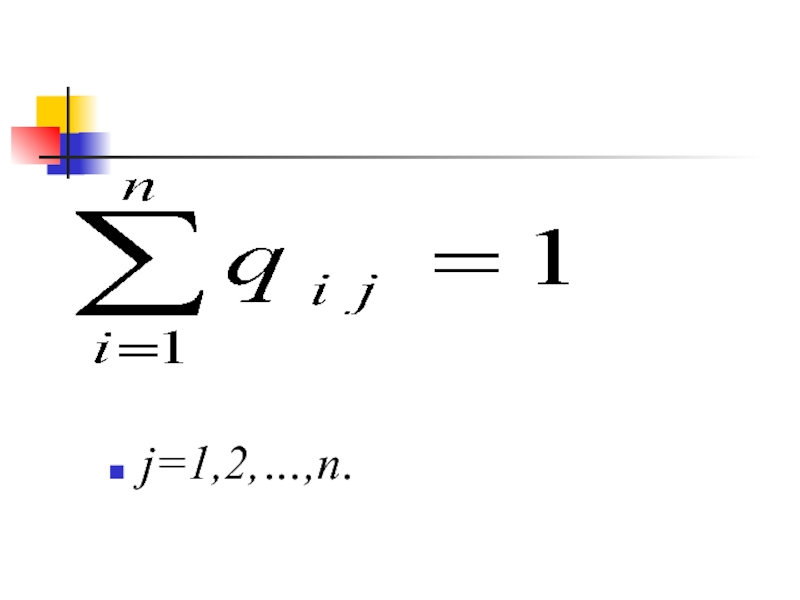Модель рівноважних цін

Содержание

1. Модель рівноважних цін
2. Слайд 2
3. Слайд 3
4. Слайд 4
5. Тоді, наприклад і-та галузь одержить
6. Так, для випуску одиниці продукції
7. На закупівлю цієї продукції
8. Отже,
9. Частину доходу, що залишилась, позначимо
10. Слайд 10
11. Слайд 11
12. Слайд 12
13. Аналогічно для інших галузей дістанемоP2 = (
14. Слайд 14
15. Слайд 15
16. Слайд 16
17. Слайд 17
18. Лінійна модель міжнародної торгівліРозглянемо лінійну модель обміну,
19. Нехай маємо групу з п
20. Слайд 20
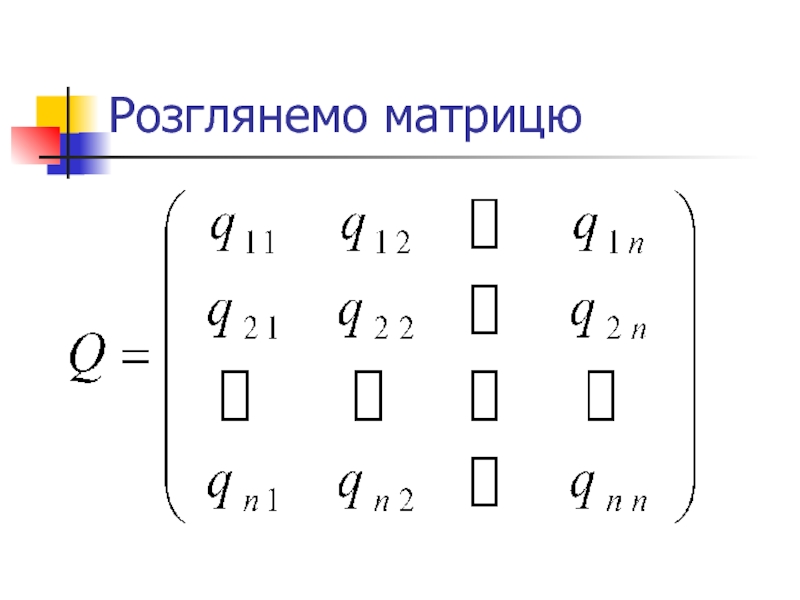
21. Розглянемо матрицю
22. Слайд 22
23. j=1,2,…,n.
24. Слайд 24
25. Для збалансованої торгівлі необхідно знайти таку матрицю
26. Слайд 26
27. Скачать презентанцию

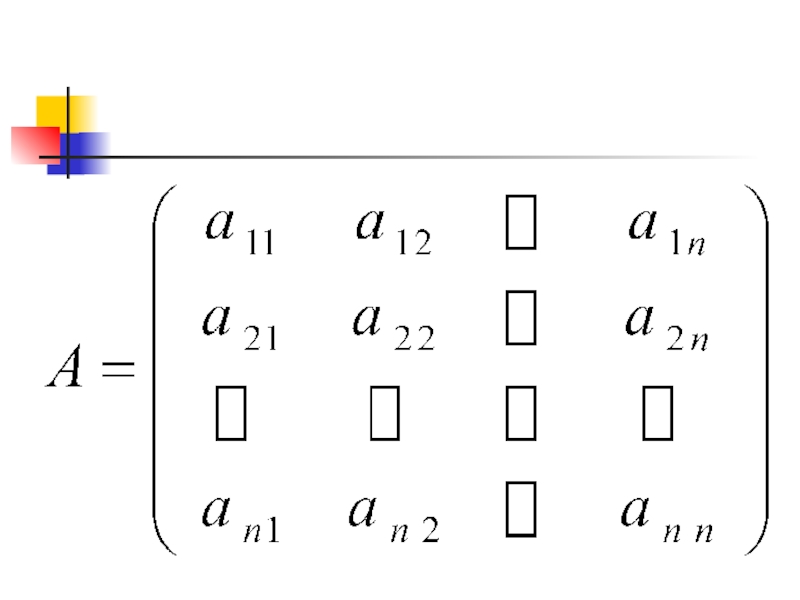
де А – матриця прямих витрат; Х – матриця обсягів валової продукції; Р – матриця цін, і-та координата якої дорівнює ціні одиниці

Главная
Разное
Модель рівноважних цін

Слайды и текст этой презентации

Слайд 1Модель рівноважних цін
Розглянемо балансову модель, яку називають моделлю

рівноважних цін.
Нехай задано матриці:

Слайд 2

Слайд 3

Слайд 4

де А – матриця прямих витрат; Х – матриця обсягів

валової продукції; Р – матриця цін, і-та координата якої дорівнює ціні одиниці продукції і-ої галузі.

Слайд 5
Тоді, наприклад і-та галузь одержить прибуток, який дорівнює

р1х1. Частину свого прибутку ця галузь витратить на закупівлю продукції

інших галузей.

Тоді, наприклад і-та галузь одержить прибуток, який дорівнює р1х1. Частину свого прибутку ця галузь витратить

Слайд 6
Так, для випуску одиниці продукції їй необхідна продукція

першої галузі в обсязі а1 1 , другої галузі –

в обсязі а2 1, n-ої галузі – в обсязі аn 1.

Так, для випуску одиниці продукції їй необхідна продукція першої галузі в обсязі а1 1 ,

Слайд 7
На закупівлю цієї продукції буде витрачено суму,

що становить
a1 1∙ p1 + a2 1∙

p2 + …+ an 1∙ pn .

На закупівлю цієї продукції буде витрачено суму, що становить a1 1∙ p1 +

Слайд 8
Отже, першій галузі

для випуску продукції в обсязі х1 необхідно витратити на закупівлю

продукції інших галузей суму, що становить
x1∙( a1 1∙ p1 + a2 1∙ p2 + …+ an 1∙ pn )

Отже, першій галузі для випуску продукції в обсязі х1 необхідно витратити

Слайд 9
Частину доходу, що залишилась, позначимо V1 (ця частина

доходу називається додатковою вартістю і йде на виплату заробітної плати

і податків, підприємницький прибуток та інвестиції).

Частину доходу, що залишилась, позначимо V1 (ця частина доходу називається додатковою вартістю і йде на

Слайд 10
Таким

чином, справджується рівність:
x1 p1 = x1∙( a1 1∙ p1

+ a2 1∙ p2 + …+ an 1∙ pn )+ V1.

Таким чином, справджується рівність: x1 p1 = x1∙(

Слайд 11
Поділивши її

на х1, дістанемо
p1 = ( a1 1∙ p1

+ a2 1∙ p2 + …+ an 1∙ pn )+ W1,

Слайд 12

де
W1= V1 / x1

– норма додаткової вартості (тобто додаткова вартість на одиницю продукції, що випускається).

Слайд 13Аналогічно для інших галузей дістанемо
P2 = ( a1 2 ∙

p1 + a2 2 ∙ p2 + …+ an 2

∙ pn )+ W2 ,
…………………………………………………………….…….
Pn = ( a1 n ∙ p1 + a2 n ∙ p2 + …+ an n ∙ pn )+ Wn .

Аналогічно для інших галузей дістанемоP2 = ( a1 2 ∙ p1 + a2 2 ∙ p2 +

Слайд 14
Отримані

рівності можна записати в матричній формі:
P = AT∙P +

W, (9)

Отримані рівності можна записати в матричній формі: P

Слайд 15

де AT – матриця, транспонована до матриці A;
W

– матриця-стовпець норм додаткової вартості.

Слайд 16
Бачимо, що

рівняння (9) відрізняються від рівнянь моделі Леонтьєва лише тим, що

матрицю обсягів валової продукції Х замінено на матрицю цін Р, матрицю обсягу кінцевої продукції Y - на матрицю додаткової вартості W, матрицю А на транспоновану матрицю AT.

Бачимо, що рівняння (9) відрізняються від рівнянь моделі Леонтьєва

Слайд 17
Модель рівноважних

цін дає змогу за відомих норм додаткової вартості прогнозувати ціни

на продукцію галузей, а також зміни цін та інфляцію, що є наслідком зміни ціни в одній із галузей.

Модель рівноважних цін дає змогу за відомих норм додаткової

Слайд 18Лінійна модель міжнародної торгівлі
Розглянемо лінійну модель обміну, яку часто інтерпретують,

як модель міжнародної торгівлі, що дає змогу визначити торгівельні доходи

країн ( або їхні співвідношення) для збалансованої торгівлі.

Лінійна модель міжнародної торгівліРозглянемо лінійну модель обміну, яку часто інтерпретують, як модель міжнародної торгівлі, що дає змогу

Слайд 19
Нехай маємо групу з п країн К1 ,

К2 , … , К п , які ведуть між

собою торгівлю. Позначимо через x j торгівельний прибуток j-ої країни, який формується з продажу власних товарів як на внутрішньому, так і на зовнішньому ринках.

Нехай маємо групу з п країн К1 , К2 , … , К п ,

Слайд 20

Структуру торгівельних відносин між країнами вважаємо встановленою: частина q i

j торгівельного прибутку x j , яку j-та країна витрачає на купівлю товарів і-тої країни, є сталою.

Слайд 21Розглянемо матрицю

Слайд 22

яку називають структурною матрицею торгівлі.

Вважатимемо, що

весь торгівельний прибуток витрачається або на закупівлю товарів на своїй території, або на імпорт з інших країн, тобто сума елементів будь-якого стовпчика матриці Q дорівнює одиниці: