Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
МОДЕЛИ, ОПИСЫВАЕМЫЕ СИСТЕМАМИ ДВУХ АВТОНОМНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
Содержание
- 1. МОДЕЛИ, ОПИСЫВАЕМЫЕ СИСТЕМАМИ ДВУХ АВТОНОМНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
- 2. Фазовая плоскость качественное моделирование свойств биологических систем
- 3. Фазовый портрет Для изображения фазового портрета необходимо
- 4. Метод изоклин Для построения фазового портрета пользуются
- 5. Главные изоклины dy/dx=0, P(x,y)=0 – изоклина горизонтальных
- 6. Фазовые траектории системы это проекции интегральных кривых
- 7. Устойчивость стационарного состоянияДля состояния равновесияСостояние равновесия устойчиво,
- 8. Линейные системы
- 9. Корни λ1, λ2 λ1, λ2 – действительны
- 10. ИССЛЕДОВАНИЕ УСТОЙЧИВОСТИ СТАЦИОНАРНЫХ СОСТОЯНИЙЛяпунов показал, что в
- 11. Получим систему первого приближения если оба корня
- 12. Грубые системы В случае, когда оба корня
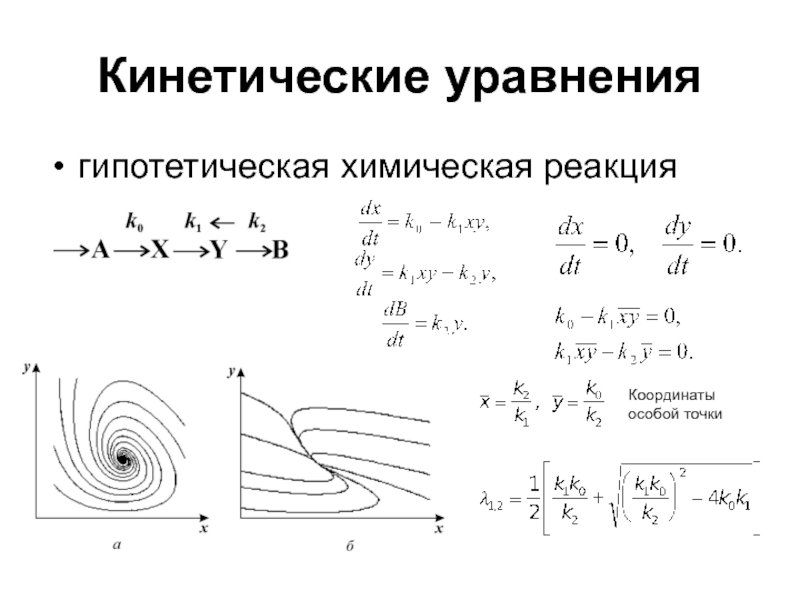
- 13. Кинетические уравнения гипотетическая химическая реакция Координатыособой точки
- 14. Модель «хищник-жертва» x - жертва и y
- 15. ПРОБЛЕМА БЫСТРЫХ И МЕДЛЕННЫХ ПЕРЕМЕННЫХ задача моделирования
- 16. Средние, быстрые и медленные времена P(x, y, z*) =0. Процесс квазистационарный
- 17. Бифуркации динамических систем Здесь x – вектор
- 18. Бифуркация седло-узел(а) - * положение равновесия исчезает.
- 19. Основные бифуркации а – фазовый портрет в
- 20. МУЛЬТИСТАЦИОНАРНЫЕ СИСТЕМЫ Важная особенность биологических систем –
- 21. Уравнения триггерных систем x1=x2=0 – неустойчивый узел;– седло – устойчивый узел; – устойчивый узел
- 22. Параметрическое переключение триггеровПри таком способе переключения непосредственному
- 23. КОЛЕБАНИЯ В БИОЛОГИЧЕСКИХ СИСТЕМАХУстойчивый (а) и неустойчивые (б и в) предельные циклы на фазовой плоскости
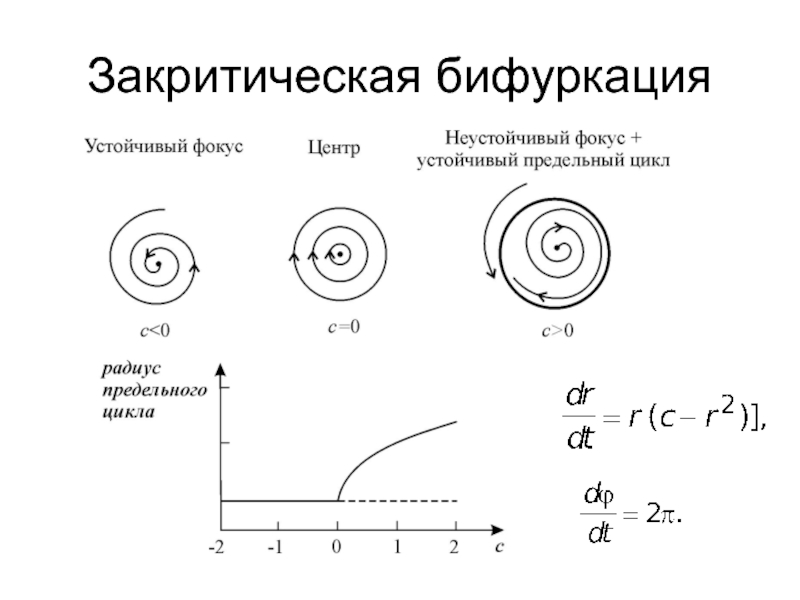
- 24. Закритическая бифуркация
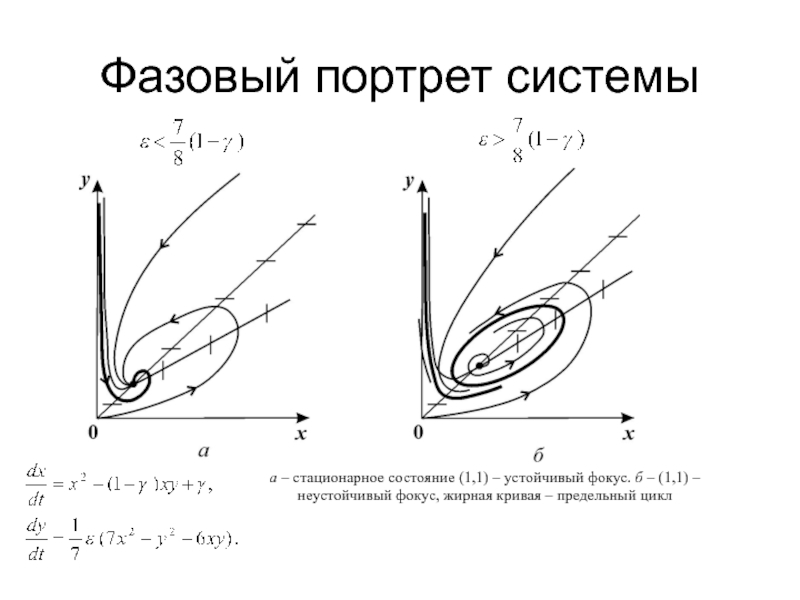
- 25. Фазовый портрет системыа – стационарное состояние (1,1)
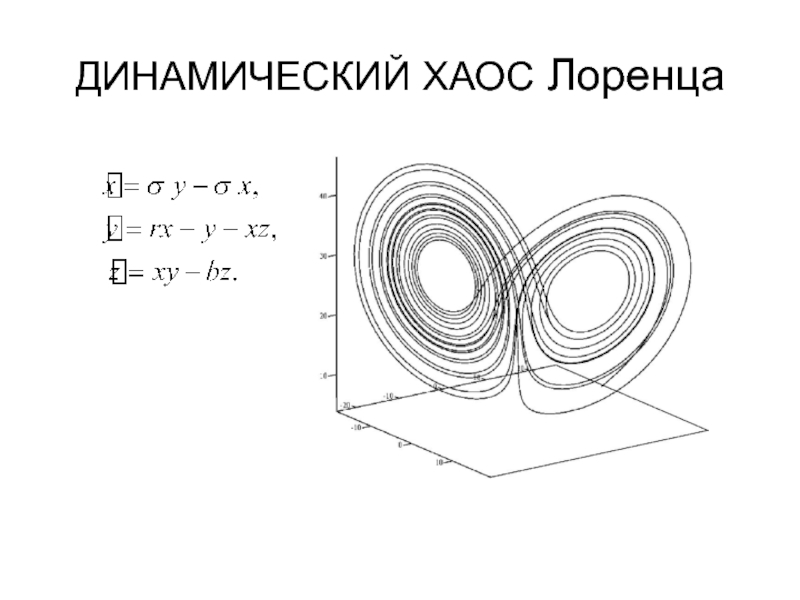
- 26. ДИНАМИЧЕСКИЙ ХАОС Лоренца
- 27. Анализ устойчивости траекторий Поиск «хаотического аттрактора». Вид
- 28. Линейный анализ устойчивости траекторийДля общей характеристики устойчивости
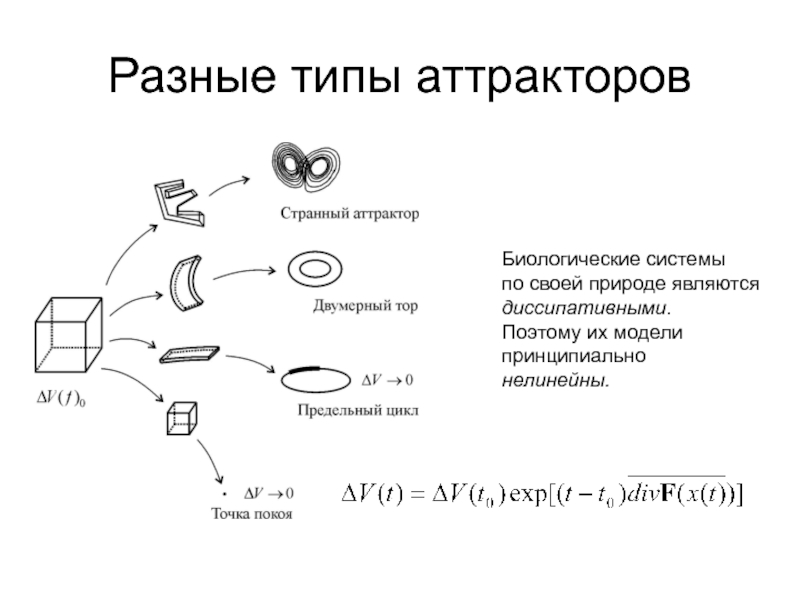
- 29. Разные типы аттракторов Биологические системы по своей природе являются диссипативными. Поэтому их модели принципиально нелинейны.
- 30. Квазистохастические изменения численностей
- 31. Скачать презентанцию
Фазовая плоскость качественное моделирование свойств биологических систем получено на моделях из двух дифференциальных уравнений с помощью метода фазовой плоскости. Каждая точка М этой плоскости соответствует определенному состоянию системы.
Слайды и текст этой презентации
Слайд 2Фазовая плоскость
качественное моделирование свойств биологических систем получено на моделях
из двух дифференциальных уравнений с помощью метода фазовой плоскости.
точка М этой плоскости соответствует определенному состоянию системы.
Слайд 3Фазовый портрет
Для изображения фазового портрета необходимо построить векторное поле
направлений траекторий системы в каждой точке фазовой плоскости. Задавая приращение
t>0, получим соответствующие приращения x и y из выражений:x=P(x,y) t,
y=Q(x,y) t.
P(x,y)>0, Q(x,y)>0
P(x,y)<0, Q(x,y)<0
P(x,y)>0, Q(x,y)<0
P(x,y)<0,
Q(x,y)>0
Слайд 4Метод изоклин
Для построения фазового портрета пользуются методом изоклин – на фазовой
плоскости наносят линии, которые пересекают интегральные кривые под одним определенным
углом.Значение А представляет собой тангенс угла наклона касательной к фазовой траектории и может принимать значения от – до +.
Это уравнение определяет в каждой точке плоскости единственную касательную к соответствующей интегральной кривой за исключением точки, где P (x,y) = 0, Q (x,y) = 0, называемой – особой точкой.
Слайд 5Главные изоклины
dy/dx=0, P(x,y)=0 – изоклина горизонтальных касательных и
dy/dx= ,
Q(x,y)=0 – изоклина вертикальных касательных.
Построив главные изоклины и найдя точку
их пересечения (x,y), координаты которой удовлетворяют условиям: 
Слайд 6Фазовые траектории системы
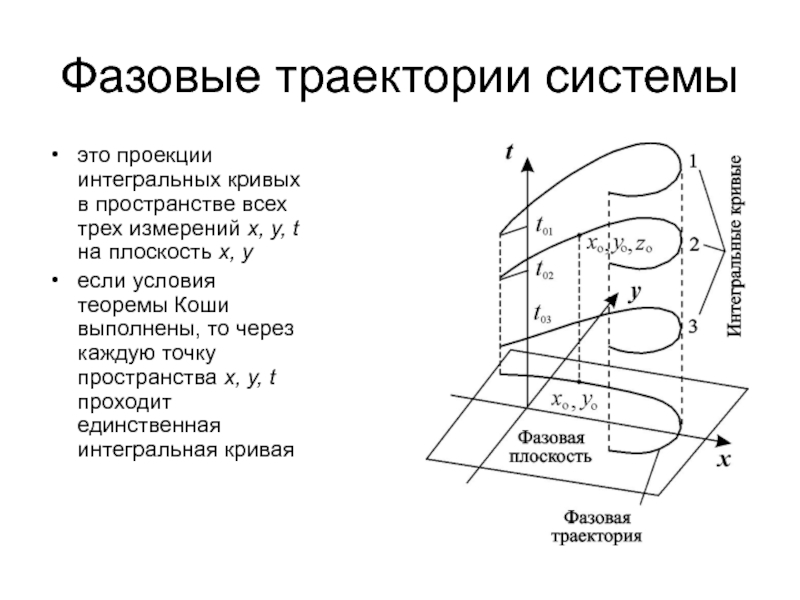
это проекции интегральных кривых в пространстве всех
трех измерений x, y, t на плоскость x, y
если условия теоремы Коши
выполнены, то через каждую точку пространства x, y, t проходит единственная интегральная кривая 
Слайд 7Устойчивость стационарного состояния
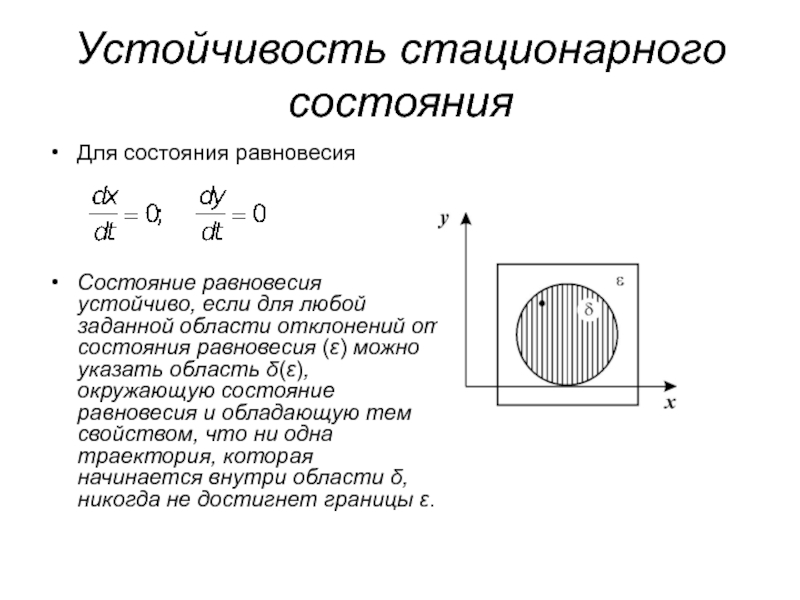
Для состояния равновесия
Состояние равновесия устойчиво, если для любой
заданной области отклонений от состояния равновесия () можно указать область
(), окружающую состояние равновесия и обладающую тем свойством, что ни одна траектория, которая начинается внутри области , никогда не достигнет границы .
Слайд 9Корни λ1, λ2
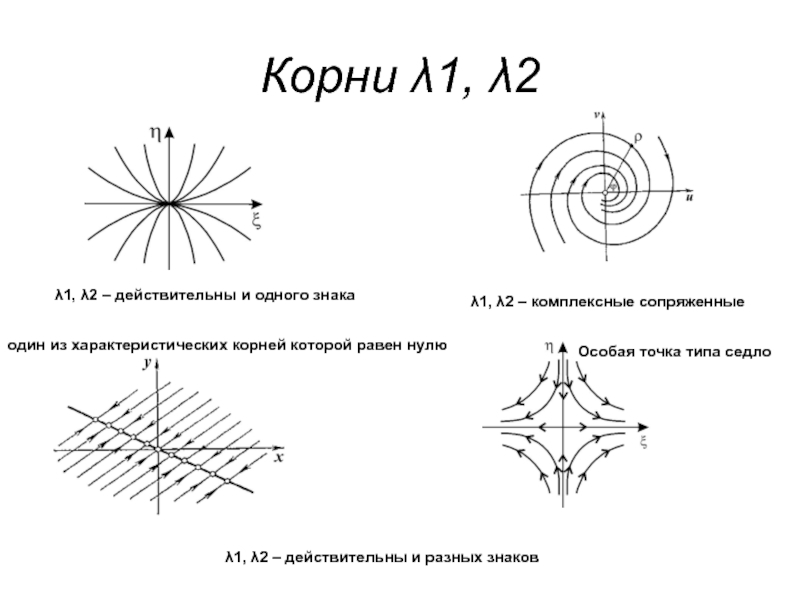
λ1, λ2 – действительны и одного знака
λ1, λ2 – действительны и разных знаков
λ1, λ2 –
комплексные сопряженные Особая точка типа седло
один из характеристических корней которой равен нулю
Слайд 10ИССЛЕДОВАНИЕ УСТОЙЧИВОСТИ СТАЦИОНАРНЫХ СОСТОЯНИЙ
Ляпунов показал, что в большом числе случаев
анализ устойчивости стационарного состояния нелинейной системы можно заменить анализом устойчивости
системы, линеаризованной в окрестности стационарного состояния.разложим правые части
уравнений в ряд Тейлора
Слайд 11Получим систему первого приближения
если оба корня имеют отрицательную действительную
часть, то состояние равновесия устойчиво;
если хотя бы один корень имеет
положительную действительную часть, то состояние равновесия неустойчиво.Если действительные части обоих корней характеристического уравнения равны нулю или если один корень равен нулю, а другой отрицателен, то необходимо рассматривать члены более высокого порядка малости в разложении в ряд Тейлора правых частей уравнений.
Слайд 12Грубые системы
В случае, когда оба корня характеристического уравнения имеют
отличные от нуля действительные части, уравнение первого приближения определяют не
только устойчивость стационарного состояния, но и характер фазовых траекторий в достаточно малой его окрестности.здесь возможны пять типов грубых состояний равновесия: устойчивый узел, неустойчивый узел, устойчивый фокус, неустойчивый фокус и седло.
Слайд 14Модель «хищник-жертва»
x - жертва и y - хищников
x = 4,
xy = 0,3,
y = yx = 0,4
x =2,
xy
= 0,3, y = yx = 0,4
Слайд 15ПРОБЛЕМА БЫСТРЫХ И МЕДЛЕННЫХ ПЕРЕМЕННЫХ
задача моделирования заключается в том,
чтобы построить модель явления, содержащую возможно меньшее число переменных и
произвольных параметров, и в то же время правильно отражающую свойства явления.учет временной иерархии процессов позволяет сократить число дифференциальных уравнений.
Слайд 17Бифуркации динамических систем
Здесь x – вектор переменных, -
вектор параметров
Зафиксируем некоторое =*, и рассмотрим фазовые портреты системы
при данном значении параметра, а также при >* и <*. Фазовые портреты топологически эквивалентны, если существует невырожденное непрерывное преобразование координат, которое переводит все элементы одного фазового портрета в элементы другого.
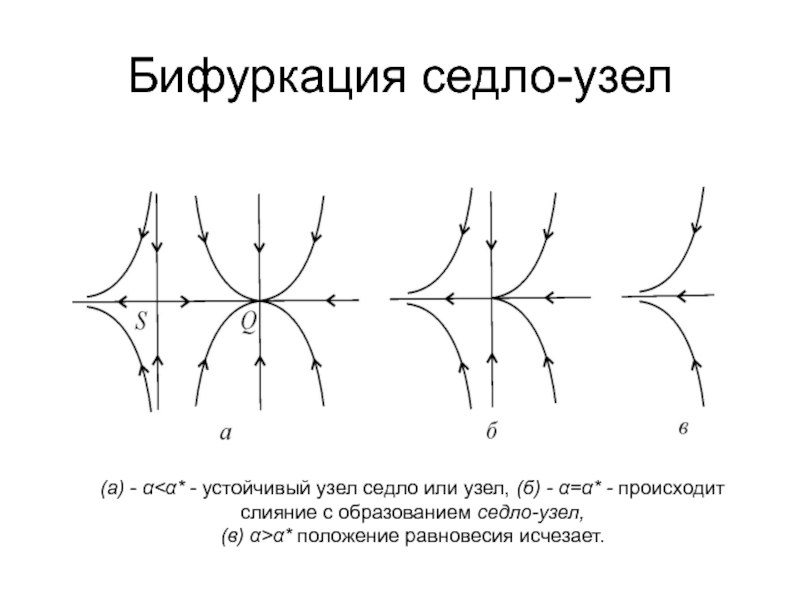
Слайд 18Бифуркация седло-узел
(а) -
(б) - =* - происходит слияние с образованием седло-узел,
(в)
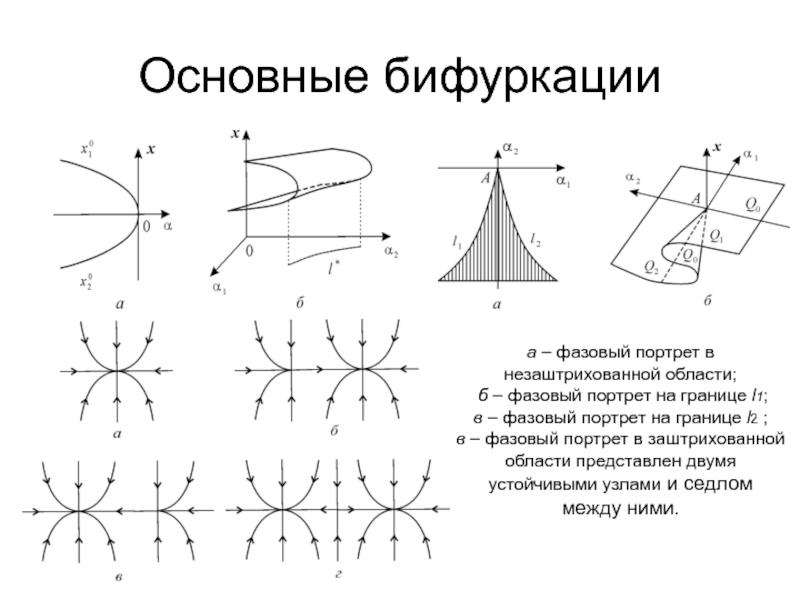
>* положение равновесия исчезает.
Слайд 19Основные бифуркации
а – фазовый портрет в
незаштрихованной области;
б
– фазовый портрет на границе l1;
в – фазовый портрет
на границе l2 ; в – фазовый портрет в заштрихованной
области представлен двумя
устойчивыми узлами и седлом
между ними.
Слайд 20МУЛЬТИСТАЦИОНАРНЫЕ СИСТЕМЫ
Важная особенность биологических систем – переключение из одного
режима функционирования в другой.
Сон и бодрствование – это разные
типы метаболизма. Переключение происходит периодически и синхронизируется геофизическим ритмом.Дифференцировка тканей – клетки получаются путем деления из одного типа клеток, но впоследствии каждая выполняет свои функции.
Фазовый портрет триггерной системы
Слайд 21Уравнения триггерных систем
x1=x2=0 – неустойчивый узел;
– седло
– устойчивый
узел;
– устойчивый узел
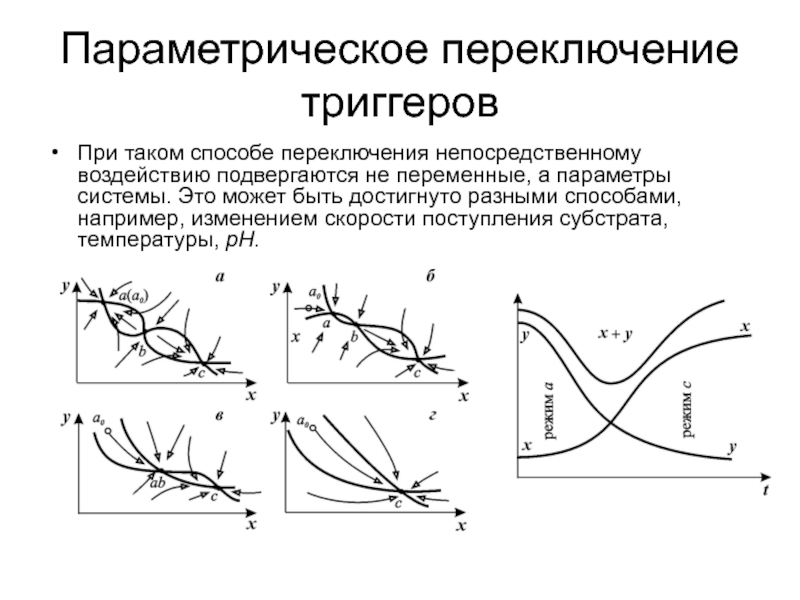
Слайд 22Параметрическое переключение триггеров
При таком способе переключения непосредственному воздействию подвергаются не
переменные, а параметры системы. Это может быть достигнуто разными способами,
например, изменением скорости поступления субстрата, температуры, рН.
Слайд 23КОЛЕБАНИЯ В БИОЛОГИЧЕСКИХ СИСТЕМАХ
Устойчивый (а) и неустойчивые (б и в)
предельные циклы на фазовой плоскости
Слайд 25Фазовый портрет системы
а – стационарное состояние (1,1) – устойчивый фокус.
б – (1,1) – неустойчивый фокус, жирная кривая – предельный
цикл
Слайд 27Анализ устойчивости траекторий
Поиск «хаотического аттрактора».
Вид проекций фазовой траектории
на странном аттракторе в
системе Ресслера.
Слайд 28Линейный анализ устойчивости траекторий
Для общей характеристики устойчивости траектории по отношению
к возмущению вдоль i-го собственного вектора используют величину, называемую характеристическим
показателем Ляпунова:Таким образом – это усредненное вдоль исследуемой траектории значение действительной части собственного значения i матрицы линеаризации.
Слайд 29Разные типы аттракторов
Биологические системы
по своей природе являются диссипативными.
Поэтому их модели
принципиально
нелинейны.
