Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Молекулярная физика
Содержание
- 1. Молекулярная физика
- 2. Фазы и фазовые превращенияПримеры превращений. Условия равновесия
- 3. Испарение. Конденсация. Кипение. Насыщенные и ненасыщенные пары
- 4. Фаза – макроскопическая физически однородная часть вещества,
- 5. Примеры1. Вода-пар → двухфазная2. Вода-пар-лед → трехфазная3. Вода-пар-лед-ртуть →
- 6. ВыводВ системе может быть несколько твердых фаз
- 7. Основной вопрос- условия равновесия фаз →
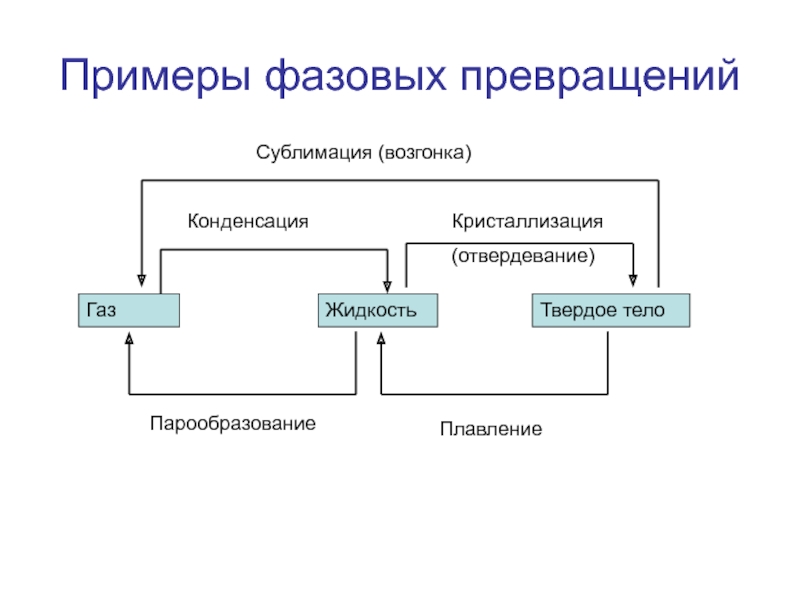
- 8. Кристаллизация (отвердевание)Примеры фазовых превращенийГазЖидкостьТвердое телоПарообразованиеПлавлениеСублимация (возгонка)Конденсация
- 9. Фазовое равновесие – не есть статическое состояниеПример:
- 10. Испарение, конденсацияИспарением называется фазовый переход из жидкого
- 11. Двухфазная системаВ закрытом сосуде жидкость и ее
- 12. Слайд 12
- 13. Если через крайние точки горизонтальных участков семейства
- 14. Равновесная температураЧисло молекул, вылетающих с единицы площади
- 15. Состояние температурыПри повышении температуры давление насыщенного пара
- 16. Если изотермически сжимать ненасыщенный пар при T
- 17. Жидкое состояниеИз газообразного состояния в жидкое можно
- 18. Относительная влажностьВ атмосферном воздухе всегда присутствуют пары
- 19. Ненасыщенный парНенасыщенный пар можно теоретически описывать с
- 20. Давление насыщенного параДавление p0 насыщенного пара очень
- 21. Процесс кипенияИспарение может происходить не только с
- 22. Атмосферное давлениеВ частности, при нормальном атмосферном давлении
- 23. РавновесиеВ герметически закрытом сосуде жидкость кипеть не
- 24. В термодинамике вводится понятие фазы как совокупности
- 25. Таким образом, в однокомпонентной системе (К= 1),
- 26. Правило фаз ГиббсаГиббс установил, что число фаз
- 27. В однофазном состоянии системы, которое характеризуется тремя
- 28. Фазовые переходы I и II родаФазой называется
- 29. Фазовый переходЛюбое вещество при определенных условиях может
- 30. ЖидкостьВсе реальные газы (кислород, азот, водород и
- 31. Фазовые переходы I и II родаПереход вещества
- 32. Фазовые переходы I родаРазличают фазовые переходы двух
- 33. Фазовые переходы II родаФазовые переходы, не связанные
- 34. Фазовые переходы II родаПримерами фазовых переходов II
- 35. Фазовые переходы I и II родаФазовые переходы
- 36. * В отдельных случаях, например
- 37. Диаграмма состояния. Тройная точка Если система является
- 38. Диаграмма состоянияДля наглядного изображения фазовых превращений используется
- 39. Тройная точкаТочка, в которой пересекаются эти кривые
- 40. Термодинамика дает метод расчета кривой равновесия двух
- 41. Уравнение Клапейрона — Клаузиуса позволяет определить наклоны
- 42. Диаграмма состоянияДиаграмма состояния, строящаяся на основе экспериментальных
- 43. Диаграмма состоянияНа диаграмме состояний видно, что кривая
- 44. Изображенная на рис. картина изотерм реального газа
- 45. Процессы испарения и конденсацииНа самом деле эта
- 46. Фазовая диаграммаКривая OT, соответствующая равновесию между твердой
- 47. Атмосферное давлениеДля многих веществ давление pтр в
- 48. Слайд 48
- 49. Слайд 49
- 50. Слайд 50
- 51. Кристаллизация (отвердевание)Примеры фазовых превращенийГазЖидкостьТвердое телоПарообразованиеПлавлениеСублимация (возгонка)Конденсация
- 52. Фазовые переходы I и II родаФазой называется
- 53. Фазовые переходы I и II родаПереход вещества
- 54. Фазовые переходы I родаРазличают фазовые переходы двух
- 55. Фазовые переходы II родаФазовые переходы, не связанные
- 56. Фазовые переходы II родаПримерами фазовых переходов II
- 57. Диаграмма состояния. Тройная точка Если система является
- 58. Диаграмма состоянияДля наглядного изображения фазовых превращений используется
- 59. Тройная точкаТочка, в которой пересекаются эти кривые
- 60. Термодинамика дает метод расчета кривой равновесия двух
- 61. Уравнение Клапейрона — Клаузиуса позволяет определить наклоны
- 62. Диаграмма состояния, строящаяся на основе экспериментальных данных,
- 63. На диаграмме состояний видно, что кривая испарения
- 64. Слайд 64
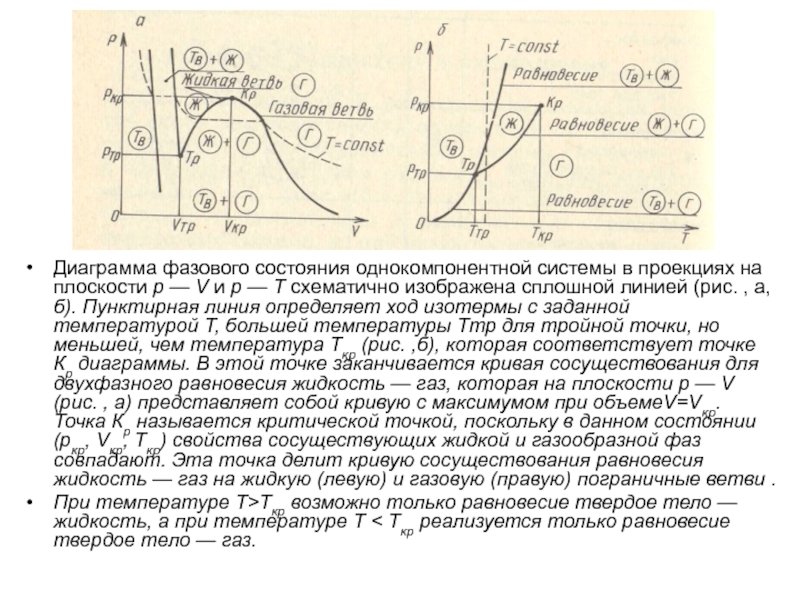
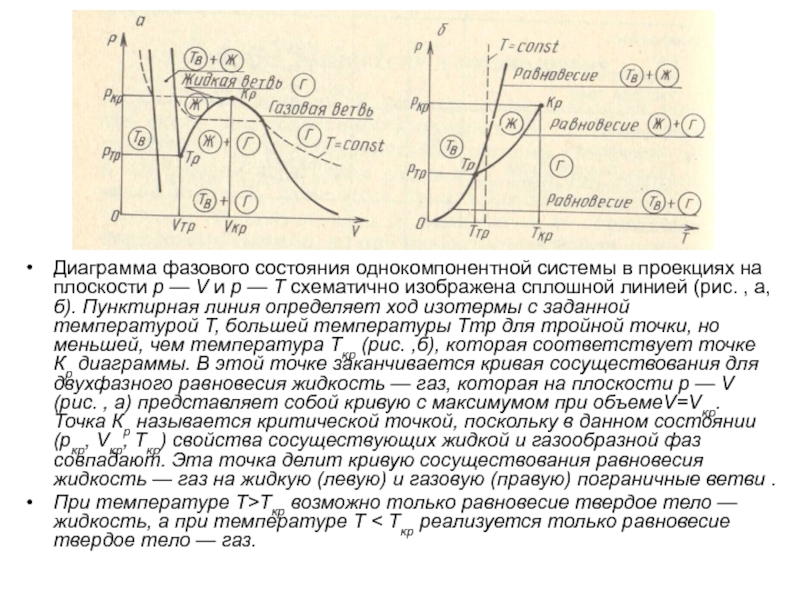
- 65. Диаграмма фазового состояния однокомпонентной системы в проекциях
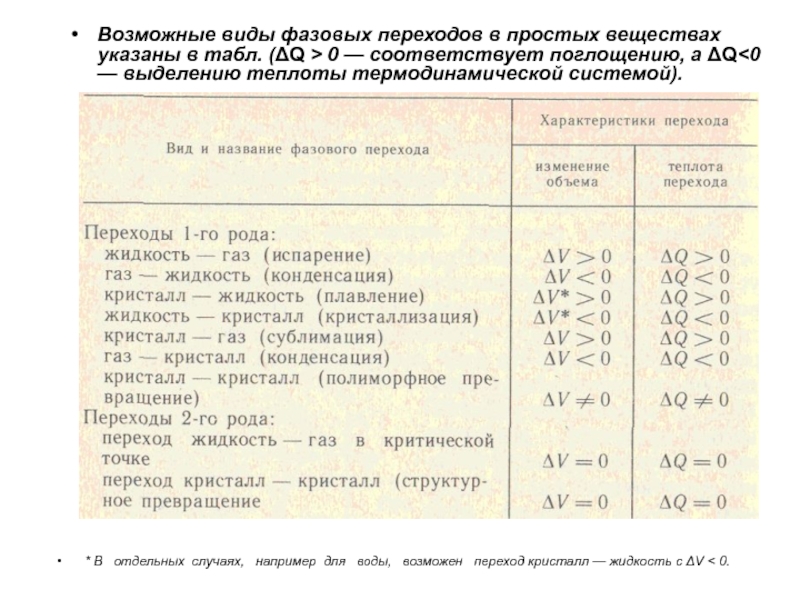
- 66. Фазовые переходы 1-го и 2-го рода. Наличие
- 67. * В отдельных случаях, например
- 68. Реализация фазовых переходов на опыте может осуществляться
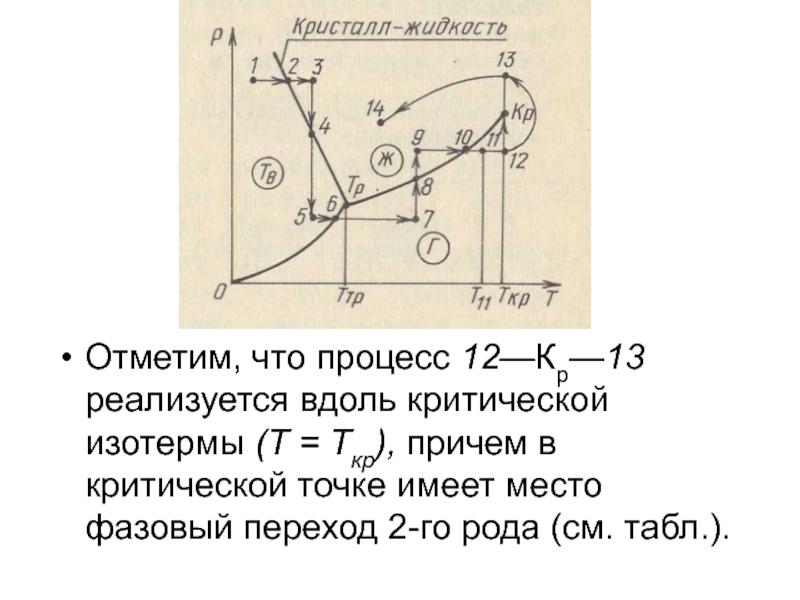
- 69. Отметим, что процесс 12—Кр—13 реализуется вдоль критической
- 70. Поскольку при фазовых превращениях 1-го рода объем
- 71. Основные понятия. В термодинамике вводится понятие фазы
- 72. Таким образом, в однокомпонентной системе (К= 1),
- 73. Правило фаз ГиббсаГиббс установил, что число фаз
- 74. В однофазном состоянии системы, которое характеризуется тремя
- 75. Диаграмма фазового состояния однокомпонентной системы в проекциях
- 76. Фазовые переходы 1-го и 2-го рода. Наличие
- 77. * В отдельных случаях, например
- 78. Слайд 78
- 79. Реализация фазовых переходов на опыте может осуществляться
- 80. Отметим, что процесс 12—Кр—13 реализуется вдоль критической
- 81. Поскольку при фазовых превращениях 1-го рода объем
- 82. Слайд 82
- 83. Слайд 83
- 84. Термодинами́ческая фа́за — термодинамически однородная по составу и
- 85. Основные понятия Газ всегда состоит из одной
- 86. Термодинамические фазы на фазовой диаграмме На фазовой
- 87. Термодинамические фазы и агрегатные состояния вещества Набор
- 88. Выделение фаз Выделение фаз — превращение гомогенной системы
- 89. Пра́вило фаз (или Правило фаз Гиббса) —
- 90. Правило фаз записывается следующим образом:j + v
- 91. Слайд 91
- 92. Слайд 92
- 93. Слайд 93
- 94. Слайд 94
- 95. Слайд 95
- 96. Слайд 96
- 97. Слайд 97
- 98. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2Фазы и фазовые превращения
Примеры превращений.
Условия равновесия фаз химически однородного
вещества. Метастабильные и нестабильные состояния
переходах 2 родаСлайд 4Фаза – макроскопическая физически однородная часть вещества, отделенная от других
частей системы границами раздела так, что она может быть извлечена
(удалена) из системы механическим путемСлайд 5Примеры
1. Вода-пар → двухфазная
2. Вода-пар-лед → трехфазная
3. Вода-пар-лед-ртуть → четырехфазная (две жидкие
фазы, т.к. вода и ртуть не смешиваются)
4. Вода-спирт-пар-лед → трехфазная
(т.к. вода и спирт смешиваются)Слайд 6Вывод
В системе может быть несколько твердых фаз и жидких фаз,
но она не может содержать более одной газообразной фазы, т.к.
газы смешиваютсяСлайд 7Основной вопрос- условия равновесия фаз
→ тепловое равновесие T=const
→ механическое равновесие p=const
→ равновесие относительно взаимного превращения фаз
mi=constРавновесие
фаз
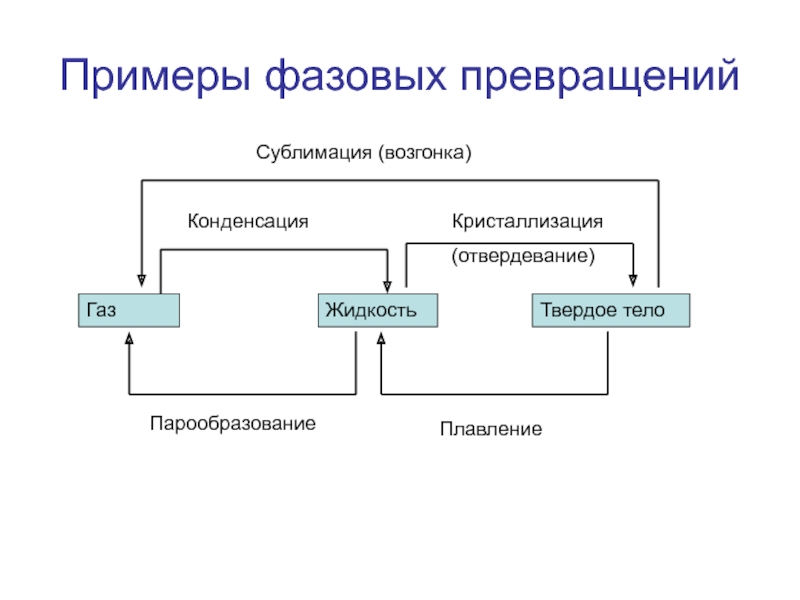
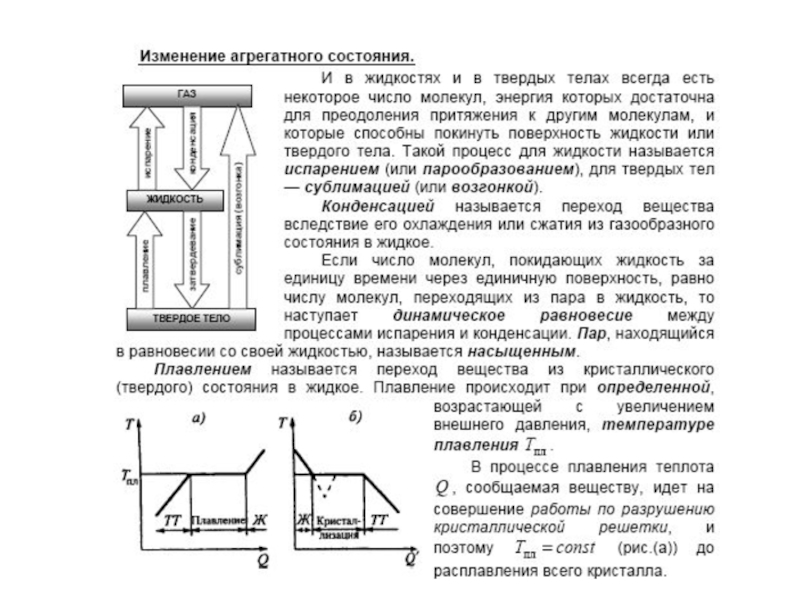
Слайд 8Кристаллизация
(отвердевание)
Примеры фазовых превращений
Газ
Жидкость
Твердое тело
Парообразование
Плавление
Сублимация (возгонка)
Конденсация
Слайд 9Фазовое равновесие – не есть статическое состояние
Пример: жидкость-пар → динамическое
равновесие
Вывод: характеристика равновесия – скорость двух противоположных процессов 1↔2, так
что количество вещества в каждой фазе = constСлайд 10Испарение, конденсация
Испарением называется фазовый переход из жидкого состояния в газообразное.
С точки зрения молекулярно-кинетической теории, испарение – это процесс, при
котором с поверхности жидкости вылетают наиболее быстрые молекулы, кинетическая энергия которых превышает энергию их связи с остальными молекулами жидкости. Это приводит к уменьшению средней кинетической энергии оставшихся молекул, т. е. к охлаждению жидкости (если нет подвода энергии от окружающих тел).Конденсация – это процесс, обратный процессу испарения. При конденсации молекулы пара возвращаются в жидкость
Слайд 11Двухфазная система
В закрытом сосуде жидкость и ее пар могут находиться
в состоянии динамического равновесия, когда число молекул, вылетающих из жидкости,
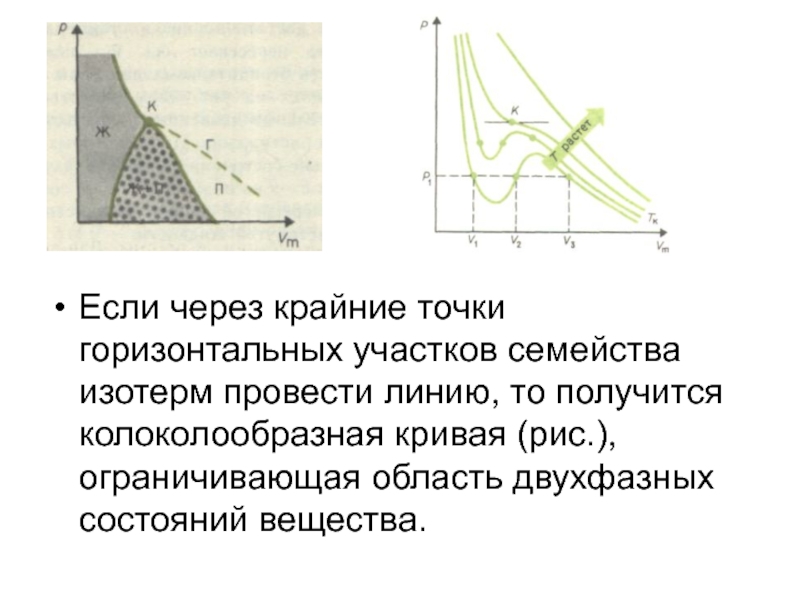
равно числу молекул, возвращающихся в жидкость из пара, т. е. когда скорости процессов испарения и конденсации одинаковы. Такую систему называют двухфазной. Пар, находящийся в равновесии со своей жидкостью, называют насыщенным.Слайд 13Если через крайние точки горизонтальных участков семейства изотерм провести линию,
то получится колоколообразная кривая (рис.), ограничивающая область двухфазных состояний вещества.
Слайд 14Равновесная температура
Число молекул, вылетающих с единицы площади поверхности жидкости за
одну секунду, зависит от температуры жидкости. Число молекул, возвращающихся из
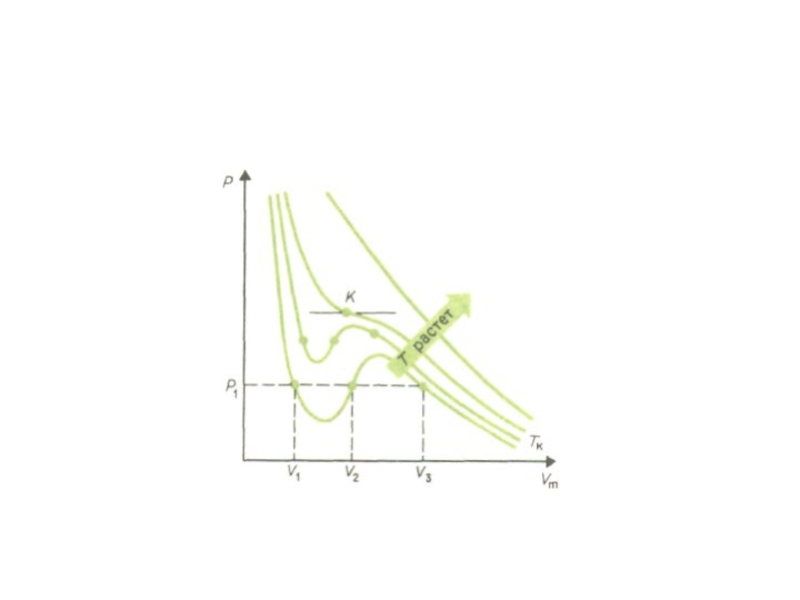
пара в жидкость, зависит от концентрации молекул пара и от средней скорости их теплового движения, которая определяется температурой пара. Отсюда следует, что для данного вещества концентрация молекул пара при равновесии жидкости и ее пара определяется их равновесной температурой. Установление динамического равновесия между процессами испарения и конденсации при повышении температуры происходит при более высоких концентрациях молекул пара. Так как давление газа (пара) определяется его концентрацией и температурой, то можно сделать вывод: давление насыщенного пара p0 данного вещества зависит только от его температуры и не зависит от объема. Поэтому изотермы реальных газов на плоскости (p, V) содержат горизонтальные участки, соответствующие двухфазной системе (рис.).Изотермы реального газа.
Область I – жидкость,
область II – двухфазная система «жидкость + насыщенный пар», область III – газообразное вещество.
K – критическая точка.
Слайд 15Состояние температуры
При повышении температуры давление насыщенного пара и его плотность
возрастают, а плотность жидкости уменьшается из-за теплового расширения. При температуре,
равной критической температуре Tкр для данного вещества, плотности пара и жидкости становятся одинаковыми. При T > Tкр исчезают физические различия между жидкостью и ее насыщенным паром.Слайд 16Если изотермически сжимать ненасыщенный пар при T
будет возрастать, пока не станет равным давлению насыщенного пара. При
дальнейшем уменьшении объема на дне сосуда образуется жидкость и устанавливается динамическое равновесие между жидкостью и ее насыщенным паром. С уменьшением объема все большая часть пара конденсируется, а его давление остается неизменным (горизонтальный участок на изотерме). Когда весь пар превращается в жидкость, давление резко возрастает при дальнейшем уменьшении объема вследствие малой сжимаемости жидкости.Слайд 17Жидкое состояние
Из газообразного состояния в жидкое можно перейти, минуя двухфазную
область. Для этого нужно совершить процесс в обход критической точки
K. Один из возможных процессов такого рода показан на рис. ломаной линией ABC.Изотермы реального газа. Область I – жидкость, область II – двухфазная система «жидкость + насыщенный пар», область III – газообразное вещество. K – критическая точка
Слайд 18Относительная влажность
В атмосферном воздухе всегда присутствуют пары воды при некотором
парциальном давлении p, которое, как правило, меньше давления насыщенного пара
p0.Отношение p / p0, выраженное в процентах, называется относительной влажностью воздуха.
Слайд 19Ненасыщенный пар
Ненасыщенный пар можно теоретически описывать с помощью уравнения состояния
идеального газа при обычных для реальных газов ограничениях: давление пара
должно быть не слишком велико (практически p ≤ (106–107) Па), а его температура выше некоторого определенного для каждого вещества значения. К насыщенному пару также можно приближенно применять законы идеального газа при условии, что для каждой температуры T давление p0 насыщенного пара определяется по кривой равновесия p0(T) для данного вещества.Слайд 20Давление насыщенного пара
Давление p0 насыщенного пара очень быстро возрастает с
ростом температуры T. Зависимость p0(T) нельзя получить из законов идеального
газа. Давление газа при постоянной концентрации молекул растет прямо пропорционально температуре. В насыщенном паре при повышении температуры возрастает не только средняя кинетическая энергия движения молекул, но и их концентрация. Поэтому давление насыщенного пара при повышении температуры возрастает быстрее, чем давление идеального газа при постоянной концентрации молекул.Слайд 21Процесс кипения
Испарение может происходить не только с поверхности, но и
в объеме жидкости. В жидкости всегда имеются мельчайшие пузырьки газа.
Если давление насыщенного пара жидкости равно внешнему давлению (т. е. давлению газа в пузырьках) или превышает его, жидкость будет испаряться внутрь пузырьков. Пузырьки, наполненные паром, расширяются и всплывают на поверхность. Этот процесс называется кипением. Таким образом, кипение жидкости начинается при такой температуре, при которой давление ее насыщенных паров становится равным внешнему давлению.Слайд 22Атмосферное давление
В частности, при нормальном атмосферном давлении вода кипит при
температуре 100 °С. Это значит, что при такой температуре давление насыщенных
паров воды равно 1 атм. При подъеме в горы атмосферное давление уменьшается, и поэтому температура кипения воды понижается (приблизительно на 1 °С на каждые 300 метров высоты). На высоте 7 км давление составляет примерно 0,4 атм, и температура кипения понижается до 70 °С.Слайд 23Равновесие
В герметически закрытом сосуде жидкость кипеть не может, т. к. при
каждом значении температуры устанавливается равновесие между жидкостью и ее насыщенным
паром. По кривой равновесия p0(T) можно определять температуры кипения жидкости при различных давлениях.Слайд 24В термодинамике вводится понятие фазы как совокупности однородных по своим
свойствам частей макроскопической системы, находящихся в одинаковом агрегатном состоянии.
Если
при некоторой температуре Т1 (рис., а) в закрытом сосуде (V=const) находится вода в равновесии с паром, т. е. двухфазная система, то при квазистатическом понижении температуры в некоторый момент времени в сосуде при Т2 = 273,15 К (t= 0°С) появятся кристаллики льда и система станет трехфазной (рис.,б). Параметры состояния, в котором сосуществуют в равновесии три фазы, определяют тройную точку данного вещества. При дальнейшем понижении температуры система вновь становится двухфазной (рис., в), состоящей в нашем случае из льда (твердая фаза) и пара (газовая фаза). Кроме упомянутых равновесий, возможно еще равновесие между жидкостью и твердым телом, а в некоторых случаях и между различными модификациями кристаллов (полиморфные превращения).Слайд 25Таким образом, в однокомпонентной системе (К= 1), состояние которой характеризуется
тремя параметрами (р, V, Т), могут быть реализованы три однофазных
состояния (Ф=1, газ, жидкость, твердое тело), три двухфазных состояния (Ф = 2, см. табл.) и одно трехфазное (Ф = 3) состояние.Слайд 26Правило фаз Гиббса
Гиббс установил, что число фаз Ф, число компонентов
смеси К и число С независимо изменяемых параметров системы (С
— число термодинамических степеней свободы) удовлетворяют следующему соотношению:С = К - Ф + 2 — правило фаз Гиббса.
Число степеней свободы С не может быть отрицательным (С≥ 0) и, следовательно, возможное число сосуществующих фаз
Ф≤К + 2
Слайд 27В однофазном состоянии системы, которое характеризуется тремя параметрами (р, V,
Т), имеется возможность независимо изменять одновременно любые два (С =
2) из трех параметров. На термодинамической рVT-диаграмме этому состоянию соответствует некоторая трехмерная область. Двухфазное состояние системы задается одной независимой переменной (С= 1), поэтому двухфазному состоянию отвечает некоторая линия в пространстве р — V — Т. Эта линия называется кривой сосуществования того или иного двухфазного состояния.При С=0 (трехфазное состояние) нет возможности изменять ни один параметр. Это означает, что такое равновесие возможно только в некоторой точке (тройная точка), т. е. при определенных значениях температуры Ттр, объема Vтр и давления ртр.
Слайд 28Фазовые переходы I и II рода
Фазой называется термодинамически равновесное состояние
вещества, отличающееся по физическим свойствам от других возможных равновесных состояний
того же вещества. Если, например, в закрытом сосуде находится вода, то эта система является двухфазной: жидкая фаза — вода; газообразная фаза — смесь воздуха с водяными парами. Если в воду бросить кусочки льда, то эта система станет трехфазной, в которой лед является твердой фазой. Часто понятие «фаза» употребляется в смысле агрегатного состояния, однако надо учитывать, что оно шире, чем понятие «агрегатное состояние». В пределах одного агрегатного состояния вещество может находиться в нескольких фазах, отличающихся по своим свойствам, составу и строению (лед, например, встречается в пяти различных модификациях - фазах).Слайд 29Фазовый переход
Любое вещество при определенных условиях может находиться в различных
агрегатных состояниях – твердом, жидком и газообразном. Переход из одного
состояния в другое называется фазовым переходом. Испарение и конденсация являются примерами фазовых переходов.Слайд 30Жидкость
Все реальные газы (кислород, азот, водород и т. д.) при определенных
условиях способны превращаться в жидкость. Однако превращение газа в жидкость
может происходить только при температурах ниже определенной, так называемой критической температуры Tкр. Например, для воды критическая температура равна 647,3 К, для азота 126 К, для кислорода 154,3 К. При комнатной температуре (≈ 300 К) вода может находиться и в жидком, и в газообразном состояниях, а азот и кислород существуют только в виде газов.Слайд 31Фазовые переходы I и II рода
Переход вещества из одной фазы
в другую — фазовый переход - всегда связан с качественными
изменениями свойств вещества. Примером фазового перехода могут служить изменения агрегатного состояния вещества или переходы, связанные с изменениями в составе, строении и свойствах вещества (например, переход кристаллического вещества из одной модификации в другую).Слайд 32Фазовые переходы I рода
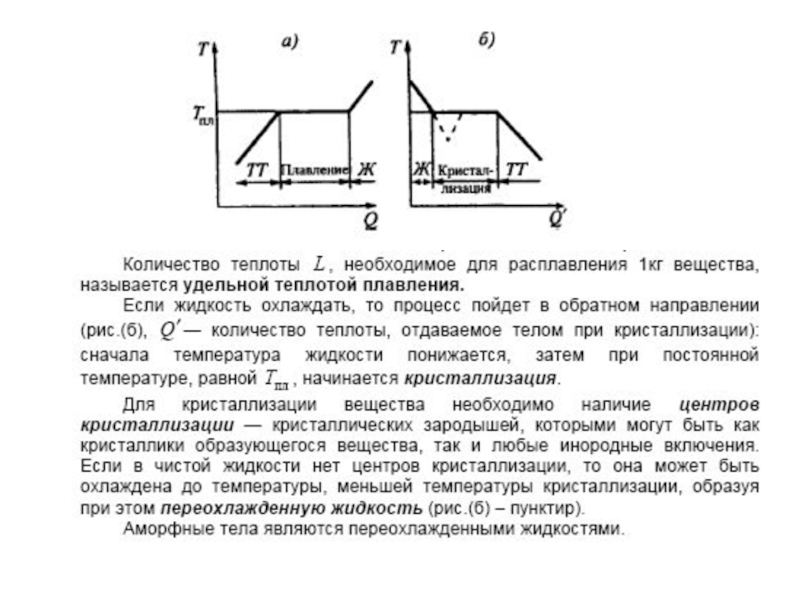
Различают фазовые переходы двух родов. Фазовый перед
I рода (например, плавление, кристаллизация и т. д.) сопровождается поглощением
или выделением теплоты, называемой теплотой фазового перехода. Фазовые переходы I рода характеризуются постоянством температуры, изменениями энтропии и объема. Объяснение этому можно дать следующим образом. Например, при плавлении телу нужно сообщить некоторое количество теплоты, чтобы вызвать разрушение кристаллической решетки. Подводимая при плавлении теплота идет не на нагрев тела, а на разрыв межатомных связей, поэтому плавление протекает при постоянной температуре. В подобных переходах — из более упорядоченного кристаллического состояния в менее упорядоченное жидкое состояние — степень беспорядка увеличивается, т. е., согласно второму началу термодинамики, этот процесс связан с возрастанием энтропии системы. Если переход происходит в обратном направлении (кристаллизация), то система теплоту выделяет.Слайд 33Фазовые переходы II рода
Фазовые переходы, не связанные с поглощением или
выделением теплоты и изменением объема, называются фазовыми переходами II рода.
Эти переходы характеризуются постоянством объема и энтропии, но скачкообразным изменением теплоемкости. Общая трактовка фазовых переходов II рода предложена ученым Л. Д. Ландау (1908—-1968). Согласно этой трактовке, фазовые переходы II рода связаны с изменением симметрии: выше точки перехода система, как правило, обладает более высокой симметрией, чем ниже точки перехода.Слайд 34Фазовые переходы II рода
Примерами фазовых переходов II рода являются: переход
ферромагнитных веществ (железа, никеля) при определенных давлении и температуре в
парамагнитное состояние; переход металлов и некоторых сплавов при температуре, близкой к 0 К, в сверхпроводящее состояние, характеризуемое скачкообразным уменьшением электрического сопротивления до нуля; превращение обыкновенного жидкого гелия (гелия I) при T = 2,9 К в другую жидкую модификацию (гелий II), обладающую свойствами сверхтекучести.Слайд 35Фазовые переходы I и II рода
Фазовые переходы 1-го и 2-го
рода. Наличие двух и трехфазных равновесий в системе означает, что
возможны превращения, в которых вещество из состояния 1, отвечающего одной сосуществующей фазе, переходит в состояние 2 с параметрами р, V, Т другой фазы. При этом может выделяться либо поглощаться определенное количество теплоты ΔQ, которая называется теплотой фазового перехода. Если в процессе превращения параметры состояния изменяются скачком на конечную величину (ΔV = V2-V1, ΔQ и т. д.), то имеет место фазовый переход 1-го рода.Фазовые переходы 2-го рода не сопровождаются выделением или поглощением теплоты (ΔQ = 0).
Слайд 36* В отдельных случаях, например для воды,
возможен переход кристалл — жидкость с ΔV
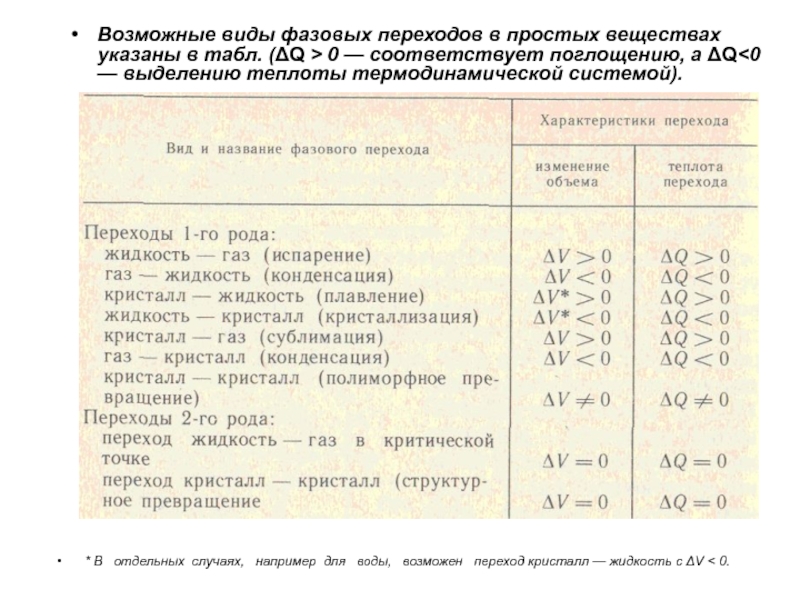
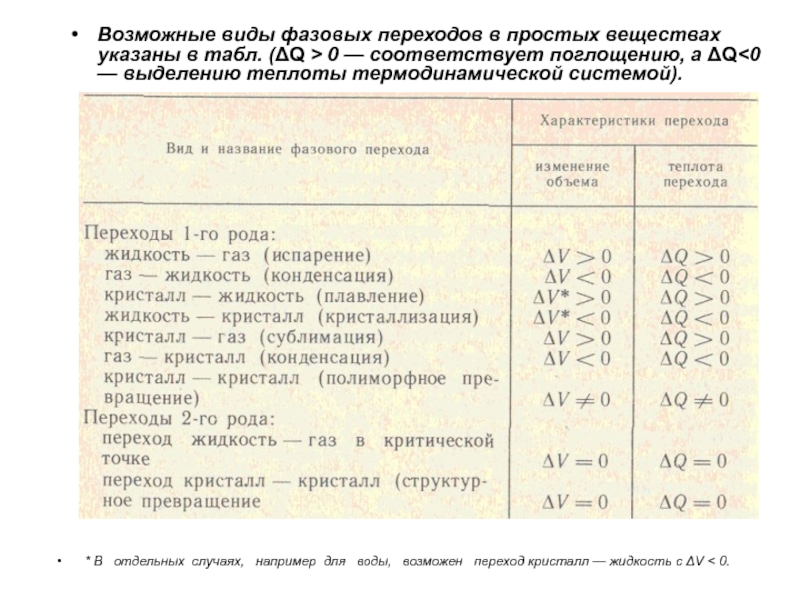
0.Возможные виды фазовых переходов в простых веществах указаны в табл. (ΔQ > 0 — соответствует поглощению, а ΔQ<0 — выделению теплоты термодинамической системой).
Слайд 37Диаграмма состояния. Тройная точка
Если система является однокомпонентной, т. е. состоящей
из химически однородного вещества или его соединения, то понятие фазы
совпадает с понятием агрегатного состояния. Одно и то же вещество в зависимости от соотношения между удвоенной средней энергией, приходящейся на одну степень свободы хаотического теплового движения молекул, и наименьшей потенциальной энергией взаимодействия молекул может находиться в одном из трех агрегатных состояний: твердом, жидком или газообразном. Это соотношение, в свою очередь, определяется внешними условиями — температурой и давлением. Следовательно, фазовые превращения также определяются изменениями температуры и давления.Слайд 38Диаграмма состояния
Для наглядного изображения фазовых превращений используется диаграмма состояния (рис.
), на которой в координатах р, Т задается зависимость между
температурой фазового перехода и давлением в виде кривых испарения (КИ), плавления (КП) и сублимации (КС), разделяющих поле диаграммы на три области, соответствующие условиям существования твердой (ТТ), жидкой (Ж) и газообразной (Г) фаз. Кривые на диаграмме называются кривыми фазового равновесия, каждая точка на них соответствует условиям равновесия двух сосуществующих фаз: КП — твердого тела и жидкости, КИ — жидкости и газа, КС — твердого тела и газа.Слайд 39Тройная точка
Точка, в которой пересекаются эти кривые и которая, следовательно,
определяет условия (температуру Tтр и соответствующее ей равновесное давление ртр)
одновременного равновесного сосуществования трех фаз вещества, называется тройной точкой. Каждое вещество имеет только одну тройную точку. Тройная точка воды характеризуется температурой 273,16 К (по шкале Цельсия ей соответствует температура 0,01 °С) и является основной реперной точкой для построения термодинамической температурной шкалы.Слайд 40Термодинамика дает метод расчета кривой равновесия двух фаз одного и
того же вещества. Согласно уравнению Клапейрона — Клаузиуса, производная от
равновесного давления по температурегде L — теплота фазового перехода, (V2-V1) —изменение объема вещества при переходе его из первой фазы во вторую, Т — температура перехода (процесс изотермический).
Слайд 41Уравнение Клапейрона — Клаузиуса позволяет определить наклоны кривых равновесия. Поскольку
L и Т положительны, наклон задается знаком V2-V1. При испарении
жидкостей и сублимации твердых тел объем вещества всегда возрастает, поэтому, dp/dT>0; следовательно, в этих процессах повышение температуры приводит к увеличению давления, и наоборот. При плавлении большинства веществ объем, как правило, возрастает, т. е. dp/dT>0; следовательно, увеличение давления приводит к повышению температуры плавления (сплошная КП на рис.). Для некоторых же веществ (Н2О, Ge, чугун и др.) объем жидкой фазы меньше объема твердой фазы, т. е. dp/dT<0; следовательно, увеличение давления сопровождается понижением температуры плавления (штриховая линия на рис. ).Слайд 42Диаграмма состояния
Диаграмма состояния, строящаяся на основе экспериментальных данных, позволяет судить,
в каком состоянии находится данное вещество при определенных р и
Т, а также какие фазовые переходы будут происходить при том или ином процессе. Например, при условиях, соответствующих точке 1 (рис. ), вещество находится в твердом состоянии, точке 2 — в газообразном, а точке 3 — одновременно в жидком и газообразном состояниях. Допустим, что вещество в твердом состоянии, соответствующем точке 4, подвергается изобарному нагреванию, изображенному на диаграмме состояния горизонтальной штриховой прямой 4—5—6. Из рисунка видно, что при температуре, соответствующей точке 5, вещество плавится, при более высокой температуре, соответствующей точке 6,— начинает превращаться в газ. Если же вещество находится в твердом состоянии, соответствующем точке 7, то при изобарном нагревании (штриховая прямая 7—8) кристалл превращается в газ минуя жидкую фазу. Если вещество находится в состоянии, соответствующем точке 9, то при изотермическом сжатии (штриховая прямая 9—10) оно пройдет следующие три состояния: газ — жидкость — кристаллическое состояние.Слайд 43Диаграмма состояния
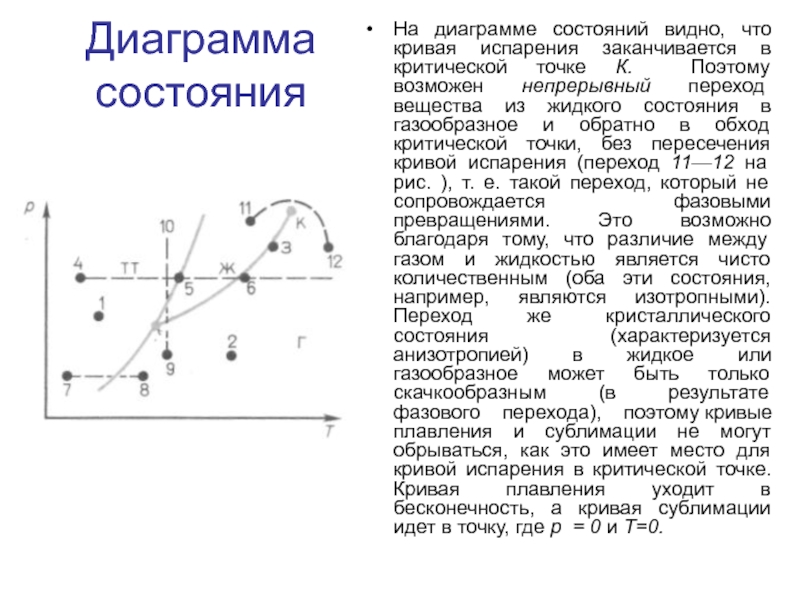
На диаграмме состояний видно, что кривая испарения заканчивается в
критической точке К. Поэтому возможен непрерывный переход вещества из жидкого
состояния в газообразное и обратно в обход критической точки, без пересечения кривой испарения (переход 11—12 на рис. ), т. е. такой переход, который не сопровождается фазовыми превращениями. Это возможно благодаря тому, что различие между газом и жидкостью является чисто количественным (оба эти состояния, например, являются изотропными). Переход же кристаллического состояния (характеризуется анизотропией) в жидкое или газообразное может быть только скачкообразным (в результате фазового перехода), поэтому кривые плавления и сублимации не могут обрываться, как это имеет место для кривой испарения в критической точке. Кривая плавления уходит в бесконечность, а кривая сублимации идет в точку, где р = 0 и Т=0.Слайд 44Изображенная на рис. картина изотерм реального газа описывает процессы испарения
и конденсации, т. е. фазовый переход между газообразной и жидкой фазами
вещества.Слайд 45Процессы испарения и конденсации
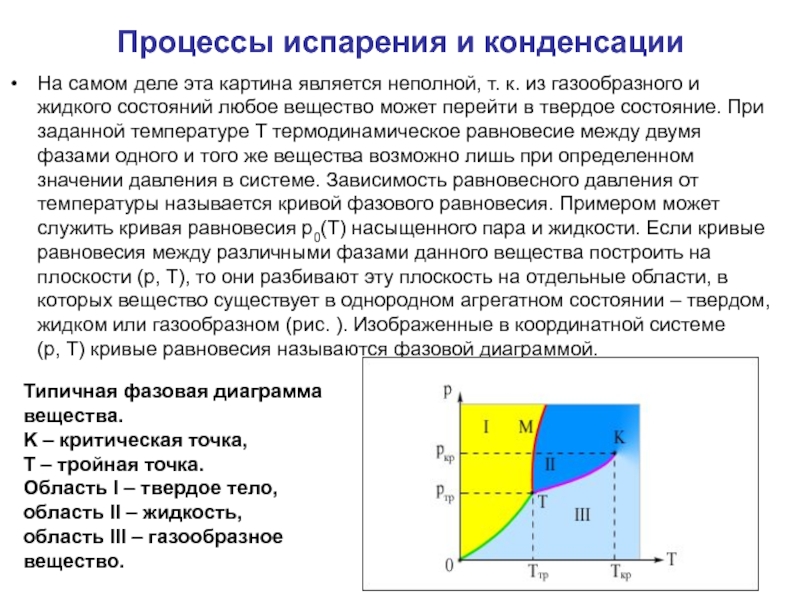
На самом деле эта картина является неполной,
т. к. из газообразного и жидкого состояний любое вещество может перейти
в твердое состояние. При заданной температуре T термодинамическое равновесие между двумя фазами одного и того же вещества возможно лишь при определенном значении давления в системе. Зависимость равновесного давления от температуры называется кривой фазового равновесия. Примером может служить кривая равновесия p0(T) насыщенного пара и жидкости. Если кривые равновесия между различными фазами данного вещества построить на плоскости (p, T), то они разбивают эту плоскость на отдельные области, в которых вещество существует в однородном агрегатном состоянии – твердом, жидком или газообразном (рис. ). Изображенные в координатной системе (p, T) кривые равновесия называются фазовой диаграммой.Типичная фазовая диаграмма вещества.
K – критическая точка,
T – тройная точка.
Область I – твердое тело,
область II – жидкость,
область III – газообразное вещество.
Слайд 46Фазовая диаграмма
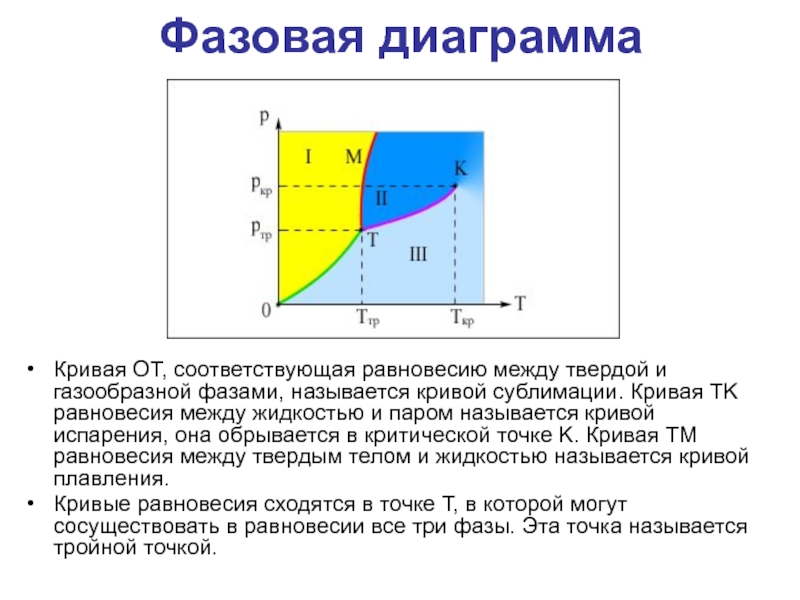
Кривая OT, соответствующая равновесию между твердой и газообразной фазами,
называется кривой сублимации. Кривая TK равновесия между жидкостью и паром
называется кривой испарения, она обрывается в критической точке K. Кривая TM равновесия между твердым телом и жидкостью называется кривой плавления.Кривые равновесия сходятся в точке T, в которой могут сосуществовать в равновесии все три фазы. Эта точка называется тройной точкой.
Слайд 47Атмосферное давление
Для многих веществ давление pтр в тройной точке меньше
1 атм ≈ 105 Па. Такие вещества при нагревании при атмосферном давлении плавятся. Например,
тройная точка воды имеет координаты Tтр = 273,16 К, pтр = 6,02·102 Па. Эта точка используется в качестве опорной для калибровки абсолютной температурной шкалы Кельвина. Существуют, однако, и такие вещества, у которых pтр превышает 1 атм. Так для углекислоты (CO2) давление pтр = 5,11 атм и температура Tтр = 216,5 К. Поэтому при атмосферном давлении твердая углекислота может существовать только при низкой температуре, а в жидком состоянии при p = 1 атм она вообще не существует. В равновесии со своим паром при атмосферном давлении углекислота находится при температуре 173 К или –80 °С в твердом состоянии. Это широко применяемый «сухой лед», который никогда не плавится, а только испаряется (сублимирует).Слайд 51Кристаллизация
(отвердевание)
Примеры фазовых превращений
Газ
Жидкость
Твердое тело
Парообразование
Плавление
Сублимация (возгонка)
Конденсация
Слайд 52Фазовые переходы I и II рода
Фазой называется термодинамически равновесное состояние
вещества, отличающееся по физическим свойствам от других возможных равновесных состояний
того же вещества. Если, например, в закрытом сосуде находится вода, то эта система является двухфазной: жидкая фаза — вода; газообразная фаза — смесь воздуха с водяными парами. Если в воду бросить кусочки льда, то эта система станет трехфазной, в которой лед является твердой фазой. Часто понятие «фаза» употребляется в смысле агрегатного состояния, однако надо учитывать, что оно шире, чем понятие «агрегатное состояние». В пределах одного агрегатного состояния вещество может находиться в нескольких фазах, отличающихся по своим свойствам, составу и строению (лед, например, встречается в пяти различных модификациях - фазах).Слайд 53Фазовые переходы I и II рода
Переход вещества из одной фазы
в другую — фазовый переход - всегда связан с качественными
изменениями свойств вещества. Примером фазового перехода могут служить изменения агрегатного состояния вещества или переходы, связанные с изменениями в составе, строении и свойствах вещества (например, переход кристаллического вещества из одной модификации в другую).Слайд 54Фазовые переходы I рода
Различают фазовые переходы двух родов. Фазовый перед
I рода (например, плавление, кристаллизация и т. д.) сопровождается поглощением
или выделением теплоты, называемой теплотой фазового перехода. Фазовые переходы I рода характеризуются постоянством температуры, изменениями энтропии и объема. Объяснение этому можно дать следующим образом. Например, при плавлении телу нужно сообщить некоторое количество теплоты, чтобы вызвать разрушение кристаллической решетки. Подводимая при плавлении теплота идет не на нагрев тела, а на разрыв межатомных связей, поэтому плавление протекает при постоянной температуре. В подобных переходах — из более упорядоченного кристаллического состояния в менее упорядоченное жидкое состояние — степень беспорядка увеличивается, т. е., согласно второму началу термодинамики, этот процесс связан с возрастанием энтропии системы. Если переход происходит в обратном направлении (кристаллизация), то система теплоту выделяет.Слайд 55Фазовые переходы II рода
Фазовые переходы, не связанные с поглощением или
выделением теплоты и изменением объема, называются фазовыми переходами II рода.
Эти переходы характеризуются постоянством объема и энтропии, но скачкообразным изменением теплоемкости. Общая трактовка фазовых переходов II рода предложена ученым Л. Д. Ландау (1908—-1968). Согласно этой трактовке, фазовые переходы II рода связаны с изменением симметрии: выше точки перехода система, как правило, обладает более высокой симметрией, чем ниже точки перехода.Слайд 56Фазовые переходы II рода
Примерами фазовых переходов II рода являются: переход
ферромагнитных веществ (железа, никеля) при определенных давлении и температуре в
парамагнитное состояние; переход металлов и некоторых сплавов при температуре, близкой к 0 К, в сверхпроводящее состояние, характеризуемое скачкообразным уменьшением электрического сопротивления до нуля; превращение обыкновенного жидкого гелия (гелия I) при T = 2,9 К в другую жидкую модификацию (гелий II), обладающую свойствами сверхтекучести.Слайд 57Диаграмма состояния. Тройная точка
Если система является однокомпонентной, т. е. состоящей
из химически однородного вещества или его соединения, то понятие фазы
совпадает с понятием агрегатного состояния. Одно и то же вещество в зависимости от соотношения между удвоенной средней энергией, приходящейся на одну степень свободы хаотического теплового движения молекул, и наименьшей потенциальной энергией взаимодействия молекул может находиться в одном из трех агрегатных состояний: твердом, жидком или газообразном. Это соотношение, в свою очередь, определяется внешними условиями — температурой и давлением. Следовательно, фазовые превращения также определяются изменениями температуры и давления.Слайд 58Диаграмма состояния
Для наглядного изображения фазовых превращений используется диаграмма состояния (рис.
), на которой в координатах р, Т задается зависимость между
температурой фазового перехода и давлением в виде кривых испарения (КИ), плавления (КП) и сублимации (КС), разделяющих поле диаграммы на три области, соответствующие условиям существования твердой (ТТ), жидкой (Ж) и газообразной (Г) фаз. Кривые на диаграмме называются кривыми фазового равновесия, каждая точка на них соответствует условиям равновесия двух сосуществующих фаз: КП — твердого тела и жидкости, КИ — жидкости и газа, КС — твердого тела и газа.Слайд 59Тройная точка
Точка, в которой пересекаются эти кривые и которая, следовательно,
определяет условия (температуру Tтр и соответствующее ей равновесное давление ртр)
одновременного равновесного сосуществования трех фаз вещества, называется тройной точкой. Каждое вещество имеет только одну тройную точку. Тройная точка воды характеризуется температурой 273,16 К (по шкале Цельсия ей соответствует температура 0,01 °С) и является основной реперной точкой для построения термодинамической температурной шкалы.Слайд 60Термодинамика дает метод расчета кривой равновесия двух фаз одного и
того же вещества. Согласно уравнению Клапейрона — Клаузиуса, производная от
равновесного давления по температурегде L — теплота фазового перехода, (V2-V1) —изменение объема вещества при переходе его из первой фазы во вторую, Т — температура перехода (процесс изотермический).
Слайд 61Уравнение Клапейрона — Клаузиуса позволяет определить наклоны кривых равновесия. Поскольку
L и Т положительны, наклон задается знаком V2-V1. При испарении
жидкостей и сублимации твердых тел объем вещества всегда возрастает, поэтому, dp/dT>0; следовательно, в этих процессах повышение температуры приводит к увеличению давления, и наоборот. При плавлении большинства веществ объем, как правило, возрастает, т. е. dp/dT>0; следовательно, увеличение давления приводит к повышению температуры плавления (сплошная КП на рис.). Для некоторых же веществ (Н2О, Ge, чугун и др.) объем жидкой фазы меньше объема твердой фазы, т. е. dp/dT<0; следовательно, увеличение давления сопровождается понижением температуры плавления (штриховая линия на рис. ).Слайд 62Диаграмма состояния, строящаяся на основе экспериментальных данных, позволяет судить, в
каком состоянии находится данное вещество при определенных р и Т,
а также какие фазовые переходы будут происходить при том или ином процессе. Например, при условиях, соответствующих точке 1 (рис. ), вещество находится в твердом состоянии, точке 2 — в газообразном, а точке 3 — одновременно в жидком и газообразном состояниях. Допустим, что вещество в твердом состоянии, соответствующем точке 4, подвергается изобарному нагреванию, изображенному на диаграмме состояния горизонтальной штриховой прямой 4—5—6. Из рисунка видно, что при температуре, соответствующей точке 5, вещество плавится, при более высокой температуре, соответствующей точке 6,— начинает превращаться в газ. Если же вещество находится в твердом состоянии, соответствующем точке 7, то при изобарном нагревании (штриховая прямая 7—8) кристалл превращается в газ минуя жидкую фазу. Если вещество находится в состоянии, соответствующем точке 9, то при изотермическом сжатии (штриховая прямая 9—10) оно пройдет следующие три состояния: газ — жидкость — кристаллическое состояние.Слайд 63На диаграмме состояний видно, что кривая испарения заканчивается в критической
точке К. Поэтому возможен непрерывный переход вещества из жидкого состояния
в газообразное и обратно в обход критической точки, без пересечения кривой испарения (переход 11—12 на рис. ), т. е. такой переход, который не сопровождается фазовыми превращениями. Это возможно благодаря тому, что различие между газом и жидкостью является чисто количественным (оба эти состояния, например, являются изотропными). Переход же кристаллического состояния (характеризуется анизотропией) в жидкое или газообразное может быть только скачкообразным (в результате фазового перехода), поэтому кривые плавления и сублимации не могут обрываться, как это имеет место для кривой испарения в критической точке. Кривая плавления уходит в бесконечность, а кривая сублимации идет в точку, где р = 0 и Т=0.Слайд 65Диаграмма фазового состояния однокомпонентной системы в проекциях на плоскости р
— V и р — Т схематично изображена сплошной линией
(рис. , а, б). Пунктирная линия определяет ход изотермы с заданной температурой T, большей температуры Tтр для тройной точки, но меньшей, чем температура Tкр (рис. ,б), которая соответствует точке Кр диаграммы. В этой точке заканчивается кривая сосуществования для двухфазного равновесия жидкость — газ, которая на плоскости р — V (рис. , а) представляет собой кривую с максимумом при объемеV=Vкр. Точка Кр называется критической точкой, поскольку в данном состоянии (ркр, Vкр, Tкр) свойства сосуществующих жидкой и газообразной фаз совпадают. Эта точка делит кривую сосуществования равновесия жидкость — газ на жидкую (левую) и газовую (правую) пограничные ветви .При температуре Т>Ткр возможно только равновесие твердое тело — жидкость, а при температуре Т < Tкр реализуется только равновесие твердое тело — газ.
Слайд 66Фазовые переходы 1-го и 2-го рода. Наличие двух и трехфазных
равновесий в системе означает, что возможны превращения, в которых вещество
из состояния 1, отвечающего одной сосуществующей фазе, переходит в состояние 2 с параметрами р, V, Т другой фазы. При этом может выделяться либо поглощаться определенное количество теплоты ΔQ, которая называется теплотой фазового перехода. Если в процессе превращения параметры состояния изменяются скачком на конечную величину (ΔV = V2-V1, ΔQ и т. д.), то имеет место фазовый переход 1-го рода.Фазовые переходы 2-го рода не сопровождаются выделением или поглощением теплоты (ΔQ = 0).
Слайд 67* В отдельных случаях, например для воды,
возможен переход кристалл — жидкость с ΔV
0.Возможные виды фазовых переходов в простых веществах указаны в табл. (ΔQ > 0 — соответствует поглощению, а ΔQ<0 — выделению теплоты термодинамической системой).
Слайд 68Реализация фазовых переходов на опыте может осуществляться в изобарических или
изотермических условиях. Примеры возможных процессов, которые сопровождаются фазовыми переходами вещества,
удобно представить графически с использованием фазовой рT-диаграммы (рис. ). На этой диаграмме в отличие от той, которая представлена на gпредыдущем рис. , б кривая сосуществования кристалл — жидкость имеет другой наклон, а именно: производная dp/dТ в данном случае меньше нуля (dр/dТ < 0), тогда как на предыдущем рис., б производная dр/dТ > 0.Из рис. видно, что переход из состояния 1 в состояние 3 является изобарическим процессом (1—2— нагревание твердого тела, 2— плавление, 2—3— нагревание жидкости), а изотермический переход 3—5 связан с расширением жидкости (3—4), кристаллизацией (точка 4) и последующим расширением вещества в твердом состоянии (4—5). Аналогично реализуются переходы 5—7, 7—9 и 9—14. Особо следует прокомментировать процесс 11—14, в котором осуществляется переход из газообразного состояния 11 в жидкое состояние 14 без фазового перехода. В этом термодинамическом процессе происходит переход системы через ряд последовательных состояний в области газа (11—12), где Т11<Т<Ткр, а затем через ряд состояний с температурой Т > Ткр (переход 12—13), которые относятся к надкритической области. Дальнейший переход из состояния 13 к состоянию 14 соответствует постепенному изменению свойств вещества в жидком состоянии.
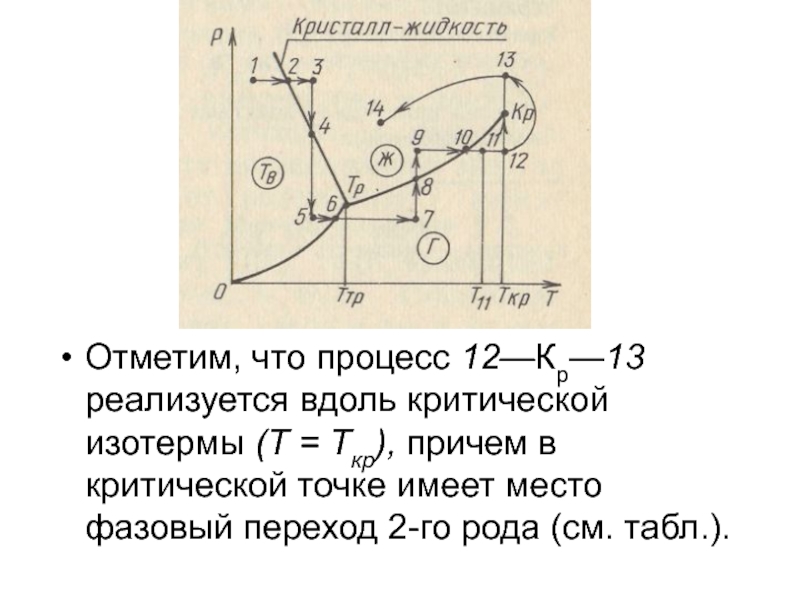
Слайд 69Отметим, что процесс 12—Кр—13 реализуется вдоль критической изотермы (Т =
Ткр), причем в критической точке имеет место фазовый переход 2-го
рода (см. табл.).Слайд 70Поскольку при фазовых превращениях 1-го рода объем системы изменяется скачком
(ΔV≠0) и выделяется или поглощается некоторое количество теплоты ΔQ, то
будут изменяться на конечную величину и другие термодинамические функции состояния (внутренняя энергия, энтропия, энтальпия и т. д.). Учитывая отсутствие универсального уравнения состояния для газов, жидкостей и твердых тел, приходится для исследования свойств вещества в различных агрегатных состояниях использовать разные и, как правило, приближенные уравнения состояния .Слайд 71Основные понятия. В термодинамике вводится понятие фазы как совокупности однородных
по своим свойствам частей макроскопической системы, находящихся в одинаковом агрегатном
состоянии.Если при некоторой температуре Т1 (рис., а) в закрытом сосуде (V=const) находится вода в равновесии с паром, т. е. двухфазная система, то при квазистатическом понижении температуры в некоторый момент времени в сосуде при Т2 = 273,15 К (t= 0°С) появятся кристаллики льда и система станет трехфазной (рис.,б). Параметры состояния, в котором сосуществуют в равновесии три фазы, определяют тройную точку данного вещества. При дальнейшем понижении температуры система вновь становится двухфазной (рис., в), состоящей в нашем случае из льда (твердая фаза) и пара (газовая фаза). Кроме упомянутых равновесий, возможно еще равновесие между жидкостью и твердым телом, а в некоторых случаях и между различными модификациями кристаллов (полиморфные превращения).
Слайд 72Таким образом, в однокомпонентной системе (К= 1), состояние которой характеризуется
тремя параметрами (р, V, Т), могут быть реализованы три однофазных
состояния (Ф=1, газ, жидкость, твердое тело), три двухфазных состояния (Ф = 2, см. табл.) и одно трехфазное (Ф = 3) состояние.Слайд 73Правило фаз Гиббса
Гиббс установил, что число фаз Ф, число компонентов
смеси К и число С независимо изменяемых параметров системы (С
— число термодинамических степеней свободы) удовлетворяют следующему соотношению:С = К - Ф + 2 — правило фаз Гиббса.
Число степеней свободы С не может быть отрицательным (С≥ 0) и, следовательно, возможное число сосуществующих фаз
Ф≤К + 2
Слайд 74В однофазном состоянии системы, которое характеризуется тремя параметрами (р, V,
Т), имеется возможность независимо изменять одновременно любые два (С =
2) из трех параметров. На термодинамической рVT-диаграмме этому состоянию соответствует некоторая трехмерная область. Двухфазное состояние системы задается одной независимой переменной (С= 1), поэтому двухфазному состоянию отвечает некоторая линия в пространстве р — V — Т. Эта линия называется кривой сосуществования того или иного двухфазного состояния.При С=0 (трехфазное состояние) нет возможности изменять ни один параметр. Это означает, что такое равновесие возможно только в некоторой точке (тройная точка), т. е. при определенных значениях температуры Ттр, объема Vтр и давления ртр.
Слайд 75Диаграмма фазового состояния однокомпонентной системы в проекциях на плоскости р
— V и р — Т схематично изображена сплошной линией
(рис. , а, б). Пунктирная линия определяет ход изотермы с заданной температурой T, большей температуры Tтр для тройной точки, но меньшей, чем температура Tкр (рис. ,б), которая соответствует точке Кр диаграммы. В этой точке заканчивается кривая сосуществования для двухфазного равновесия жидкость — газ, которая на плоскости р — V (рис. , а) представляет собой кривую с максимумом при объемеV=Vкр. Точка Кр называется критической точкой, поскольку в данном состоянии (ркр, Vкр, Tкр) свойства сосуществующих жидкой и газообразной фаз совпадают. Эта точка делит кривую сосуществования равновесия жидкость — газ на жидкую (левую) и газовую (правую) пограничные ветви .При температуре Т>Ткр возможно только равновесие твердое тело — жидкость, а при температуре Т < Tкр реализуется только равновесие твердое тело — газ.
Слайд 76Фазовые переходы 1-го и 2-го рода. Наличие двух и трехфазных
равновесий в системе означает, что возможны превращения, в которых вещество
из состояния 1, отвечающего одной сосуществующей фазе, переходит в состояние 2 с параметрами р, V, Т другой фазы. При этом может выделяться либо поглощаться определенное количество теплоты ΔQ, которая называется теплотой фазового перехода. Если в процессе превращения параметры состояния изменяются скачком на конечную величину (ΔV = V2-V1, ΔQ и т. д.), то имеет место фазовый переход 1-го рода.Фазовые переходы 2-го рода не сопровождаются выделением или поглощением теплоты (ΔQ = 0).
Слайд 77* В отдельных случаях, например для воды,
возможен переход кристалл — жидкость с ΔV
0.Возможные виды фазовых переходов в простых веществах указаны в табл. (ΔQ > 0 — соответствует поглощению, а ΔQ<0 — выделению теплоты термодинамической системой).
Слайд 79Реализация фазовых переходов на опыте может осуществляться в изобарических или
изотермических условиях. Примеры возможных процессов, которые сопровождаются фазовыми переходами вещества,
удобно представить графически с использованием фазовой рT-диаграммы (рис. ). На этой диаграмме в отличие от той, которая представлена на gпредыдущем рис. , б кривая сосуществования кристалл — жидкость имеет другой наклон, а именно: производная dp/dТ в данном случае меньше нуля (dр/dТ < 0), тогда как на предыдущем рис., б производная dр/dТ > 0.Из рис. видно, что переход из состояния 1 в состояние 3 является изобарическим процессом {1—2— нагревание твердого тела, 2— плавление, 2—3— нагревание жидкости), а изотермический переход 3—5 связан с расширением жидкости (3—4), кристаллизацией (точка 4) и последующим расширением вещества в твердом состоянии (4—5). Аналогично реализуются переходы 5—7, 7—9 и 9—14. Особо следует прокомментировать процесс 11—14, в котором осуществляется переход из газообразного состояния 11 в жидкое состояние 14 без фазового перехода. В этом термодинамическом процессе происходит переход системы через ряд последовательных состояний в области газа (11—12), где Т11<Т<Ткр, а затем через ряд состояний с температурой Т > Ткр (переход 12—13), которые относятся к надкритической области. Дальнейший переход из состояния 13 к состоянию 14 соответствует постепенному изменению свойств вещества в жидком состоянии.
Слайд 80Отметим, что процесс 12—Кр—13 реализуется вдоль критической изотермы (Т =
Ткр), причем в критической точке имеет место фазовый переход 2-го
рода (см. табл.).Слайд 81Поскольку при фазовых превращениях 1-го рода объем системы изменяется скачком
(ΔV≠0) и выделяется или поглощается некоторое количество теплоты ΔQ, то
будут изменяться на конечную величину и другие термодинамические функции состояния (внутренняя энергия, энтропия, энтальпия и т. д.). Учитывая отсутствие универсального уравнения состояния для газов, жидкостей и твердых тел, приходится для исследования свойств вещества в различных агрегатных состояниях использовать разные и, как правило, приближенные уравнения состояния .Слайд 84Термодинами́ческая фа́за — термодинамически однородная по составу и свойствам часть термодинамической
системы, отделенная от других фаз поверхностями раздела, на которых скачком
изменяются некоторые свойства системы.Другое определение:
Фаза — гомогенная часть гетерогенной системы.
В однокомпонентной системе разные фазы могут быть представлены различными агрегатными состояниями или разными полиморфными модификациями вещества. В многокомпонентной системе фазы могут иметь различный состав и структуру.
Слайд 85Основные понятия
Газ всегда состоит из одной фазы, жидкость может
состоять из нескольких жидких фаз разного состава (жидкостная несмешиваемость), но
двух разных жидкостей одного состава в равновесии сосуществовать не может. Вещество в твердом состоянии может состоять из нескольких фаз, причем некоторые из них могут иметь одинаковый состав, но различную структуру (полиморфные модификации).Разные фазы обладают различными вариантами упаковки молекул (для кристаллических фаз, различными кристаллическими решетками), и, следовательно, своими характерными значениями коэффициента сжимаемости, коэффициента теплового расширения и прочими характеристиками. Кроме того, различные фазы могут обладать разными электрическими (сегнетоэлектрики), магнитными (ферромагнетики), и оптическими свойствами (например, твёрдый кислород).
Слайд 86Термодинамические фазы на фазовой диаграмме
На фазовой диаграмме вещества различные
термодинамические фазы занимают определённые области. Линии, разделяющие различные термодинамические фазы,
называются линиями фазового перехода. Если вещество находится в условиях, отвечающих точке внутри какой-либо области, то оно полностью находится в этой термодинамической фазе. Если же состояние вещества отвечает точке на одной из линий фазовых переходов, то вещество в термодинамическом равновесии может находиться частично в одной, а частично в другой фазе. Пропорция двух фаз определяется, как правило, полной энергией, запасённой системой.При медленном (адиабатическом) изменении давления или температуры вещество описывается движущейся точкой на фазовой диаграмме. Если эта точка в своём движении пересекает одну из линий, разделяющих термодинамические фазы, происходит фазовый переход, при котором физические свойства вещества меняются скачкообразно.
Не все фазы полностью отделены друг от друга линией фазового перехода. В некоторых случаях эта линия может обрываться, оканчиваясь критической точкой. В этом случае возможен постепенный, а не скачкообразный переход из одной фазы в другую, в обход линии фазовых переходов.
Точка на фазовой диаграмме, где сходятся три линии фазовых переходов, называется тройной точкой. Обычно под тройной точкой вещества подразумевается частный случай, когда сходятся линии плавления, кипения и сублимации, однако на достаточно богатых фазовых диаграммах может быть несколько тройных точек. Вещество в тройной точке в состоянии термодинамического равновесия может частично находиться во всех трёх фазах. На многомерных фазовых диаграммах (то есть если кроме температуры и давления присутствуют иные интенсивные величины) могут существовать четверные и т. д. точки.
Фазовая диаграмма типичного вещества, имеющего твёрдую, жидкую и газообразную фазу
Слайд 87Термодинамические фазы и агрегатные состояния вещества
Набор термодинамических фаз вещества
обычно значительно богаче набора агрегатных состояний, т.е. одно и то
же агрегатное состояние вещества может находиться в различных термодинамических фазах. Именно поэтому описание вещества в терминах агрегатных состояний довольно огрублённое, и оно не может различить некоторые физические разные ситуации.Богатый набор термодинамических фаз связан, как правило, с различными вариантами порядка, которые допускаются в том или ином агрегатном состоянии.
В газообразном состоянии вещество не обладает никаким порядком. Соответственно, в газообразном состоянии любое вещество обладает только одной термодинамической фазой. (Фазовые переходы типа диссоциации молекул или ионизации являются, по определению, переходами одного вещества в другое).
Жидкость обладает трансляционным порядком, но, как правило, не обладает ориентационным порядком. В результате у одной и той же жидкости могут быть разные термодинамические фазы, однако количество их редко превышает единицу. Так, например, существование новой жидкой фазы обнаружено в переохлаждённой воде. Другой, специфический, пример: сверхтекучее состояние в жидком гелии.
Кристаллическое твёрдое тело обладает как трансляционным, так и ориентационным порядком. В результате даже возникает большое число возможных вариантов ориентации соседних молекул друг относительно друга, которые могут оказаться энергетически выгодными при тех или иных давлении и температуре. В результате твёрдые тела обладают, как правило, достаточно сложной фазовой диаграммой. Например, фазовая диаграмма такого, казалось бы, простого вещества, как лёд, насчитывает по крайней мере 12 термодинамических фаз, реализующихся при различных температурах и давлениях.
Слайд 88Выделение фаз
Выделение фаз — превращение гомогенной системы в двухфазную (или
с числом фаз более двух) широко используется в науке и
технике.Кристаллизация позволяет получать чистые вещества.
При высоких давлениях может наблюдаться такое явление, как расслоение в системе газ — газ. На возможность существования гетерогенного равновесия в газовой смеси выше критической температуры было указано ещё Ван-дер-Ваальсом и затем она была проанализирована Камерлинг-Оннесом и Кеезомом. Экспериментальное доказательство наличия такого явления было впервые получено на примере системы аммиак — азот в 1941 г. В начале предполагалось, что ограниченная взаимная растворимость наблюдается лишь в газовых смесях, содержащих полярный компонент (аммиак, сероводород). Однако впоследствии было установлено расслоение смесей гелий — диоксид углерода, гелий — этилен и гелий — пропан. В системе гелий — этилен существование поверхности раздела фаз при ограниченной взаимной растворимости газов было подтверждено визуальными наблюдениями и фотографированием мениска между двумя газовыми фазами. При расслоении смеси газов иногда наблюдается так называемое баротропное явление — перемена местами двух сосуществующих фаз при увеличении давления. К примеру, в двойной системе NH3(ж.) — N2(г.) фаза, более богатая аммиаком имеет большую плотность. Однако при расслоении смеси (90 °C, 1800 ат (~1,84 кбар)) фаза, более богатая аммиаком имеет уже меньшую плотность и поднимается вверх.[1]
Слайд 89Пра́вило фаз (или Правило фаз Гиббса) — соотношение, связывающее число
веществ (компонентов), фаз и степеней свободы в гетерогенной системе. Это
правило говорит, что в состоянии равновесия системы может одновременно существовать только конечное количество фаз.Слайд 90Правило фаз записывается следующим образом:
j + v = k +
n
где j — число фаз (например, агрегатное состояние), v
— число степеней свободы, k — компоненты системы (примеры: H2O, CO2), n — число параметров, определяющих равновесное состояние системы.При переменном давлении (т. е. для жидкостей и газов, т. к. изменение давления на состояние твёрдого тела практически не влияет) правило фаз сводится к выражению:
j + v = k + 2.
В случае однокомпонентной системы оно упрощается до:
j + v = 3,
что значит, что в однокомпонентной системе при заданном давлении и температуре могут сосуществовать три фазы. На фазовой диаграмме это соответствует тройной точке.
При изменении либо давления, либо температуры могут сосуществовать две фазы и вторая переменная зависима, что соответствует линии. Если фаза одна, то число степеней системы равно двум, и температура и давление могут меняться до тех пор, пока система не окажется на одной из ограничивающих область линий.