Момент образования трещин в изгибаемых элементах по способу ядровых

изгибаемых, внецентренно сжатых, а также внецентренно растянутых элементов по образованию

трещин производится из условия:

Где момент внешних сил, расположенных по одну сторону от рассматриваемого сечения, относительно оси, параллельной нулевой линии и проходящей через ядровую точку, наиболее удаленную от растянутой зоны, трещинообразование которой проверяется

оси элемента, при образовании трещин и опреде­ляемый по формуле:
где Мrp

— момент усилия Р относительно той же оси, что и для определения Мr; знак момента определяется направлением вращения., т.е.

упругопластический момент сопротивления железобетонного сечения по растянутой зоне в предположении, что продольная сила отсутствует;

эксцентриситет усилия обжатия относительно центра тяжести приведенного сечения;

r - расстояние от ядровой точки, наиболее удаленной от растянутой зоны, до центра тяжести приведенного сечения.

раскрытию трещин.
Ширина раскрытия трещин, нормальных к продольной оси элемента, представляет

собой разность удлинений арматуры и растянутого бетона на участке между трещинами длиной , т.е.

Средней деформацией растянутого бетона как величиной малой в сравнении со средней деформацией растянутой арматуры обычно пренебрегают и принимают

или

определяют по формуле 144 СНиП 2.03.01-84*.
где  - коэффициент, учитывающий

напряженное состояние элемента;
l  коэффициент, учитывающий длительность действия нагрузки;
— коэффициент, зависящий от вида и профиля продольной
растянутой арматуры;
s — напряжение в продольной арматуре или приращение напряжений
после погашения обжатия в растянутой арматуре;
— коэффициент армирования сечения;
d — диаметр арматуры, мм.

трещин, нормальных к продольной оси элемента acrc, мм определяют:

трещине и между трещинами силами сцепления:
где а – периметр арматурных

стержней.

По п. 7.2.14 СП 52-101-2003 значение базового расстояния между трещинами определяют

, но

(acrc2) с последующим закрытием.
При сумме постоянной и длительно действующих нагрузок

g+gдлит – трещин быть не должно, при добавлении к этой сумме кратковременной нагрузки gкрат – трещины открываются. Как только нагрузку gкрат убирают, трещины закрываются (склеиваются).
3.      трещины допускаются непродолжительные (acrc2) и продолжительные (acrc1).
При сумме постоянной и длительно действующих нагрузок g+gдлит – трещин допускаются ограниченной ширины acrc1, при добавлении к этой сумме кратковременной нагрузки gкрат – образуются трещины acrc2

оси элемента, должно быть обеспечено в предварительно напряженных конструкциях, отвечающих

требованиям 2-ой категории трещиностойкости. Это обусловлено тем, что для коррозии арматуры наиболее опасно продолжительное раскрытие трещин.
Для надежного закрытия трещин, нормальных к продольной оси элемента, должно соблюдаться 2 условия:
1. ,
где предварительное напряжение в арматуре с учетом всех потерь; приращение растягивающего напряжения в арматуре от действия внешних нагрузок.
2. сечение с трещиной в растянутой зоне при постоянной и длительной нагрузках должно оставаться обжатым с нормальными напряжениями на растягиваемой внешними нагрузками грани
.
Если нет преднапряжения, то расчет ведут по 3 категории трещиностойкости.
 

и углов поворота – связан с определением кривизны оси при

изгибе или с определением жесткости элементов. По длине железобетонного элемента в зависимости от вида нагрузки и характера напряженного состояния могут быть участки без трещин (или участки, где трещины закрыты) и участки, где в растянутой зоне есть трещины. Элементы, или участки элементов не имеют трещин в растянутой зоне, если при действии постоянных, длительных и краковременных нагрузок с коэффициентом надежности по нагрузке трещины не образуются.

учитывать влияние поперечных сил на их прогиб. В этом случае

полный прогиб ftot равен сумме прогибов, обусловленных соответственно деформацией изгиба fm и деформацией сдвига fq.
 

Прогиб fm, обусловленный деформацией изгиба, определяется по формуле (171) СНиП 2.03.01 –84*:

где изгибающий момент в сечении х от действия единичной силы, приложенной по направлению искомого перемещения элемента в сечении х по длине пролета, для которого определяется прогиб;

полная кривизна элемента в сечении х от нагрузки, при которой

определяется прогиб; знак принимается в соответствии с эпюрой кривизны.

сечения
1 – схема расположения нагрузки;
2 – эпюра изгибающих моментов;
3 –

эпюра кривизны

зоне.
На участках, где не образуются нормальные к продольной оси трещины,

полная величина кривизны изгибаемых, внецентренно сжатых и внецентренно растянутых элементов определяется по формуле (155) СНиП 2.03.01-84*

где — кривизна от действия кратковременных  нагрузок, определяемых согласно указаниям п. 1.12* СНиП 2.03.01-84*.

— кривизна от действия постоянных и длительных временных нагрузок (без учета усилия Р).

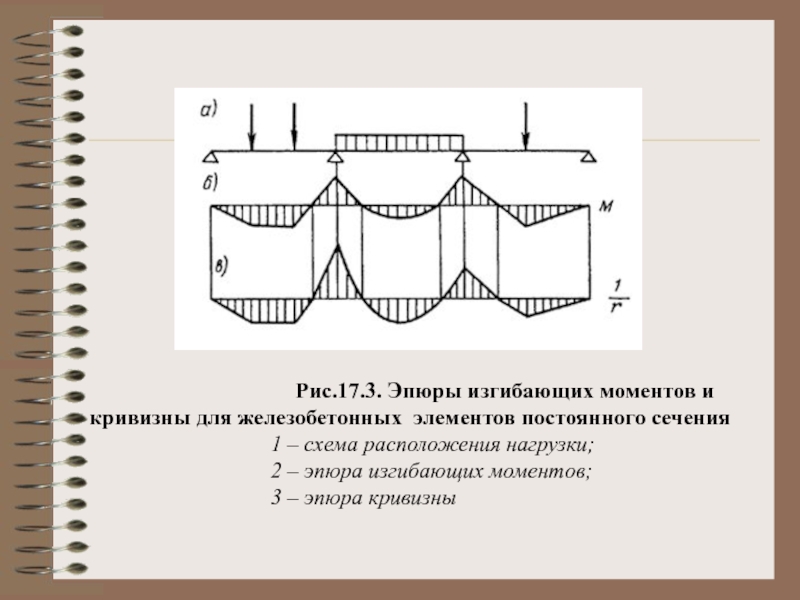
относительно оси, нормаль­ной к плоскости действия изгибаю­щего момента и проходящей

через центр тяжести приведенного сечения;
φb1 — коэффициент, учитывающий влияние кратковременной ползучести бетона.
φb2 — коэффициент, учитывающий влияние длительной ползучести бетона на де­формации элемента без трещин.

— кривизна, обусловленная выгибом элемента от кратковременного действия усилия предварительного обжатия Р 

— кривизна, обусловленная выгибом элемента вследствие усадки и ползучести бетона от усилия предварительного обжатия

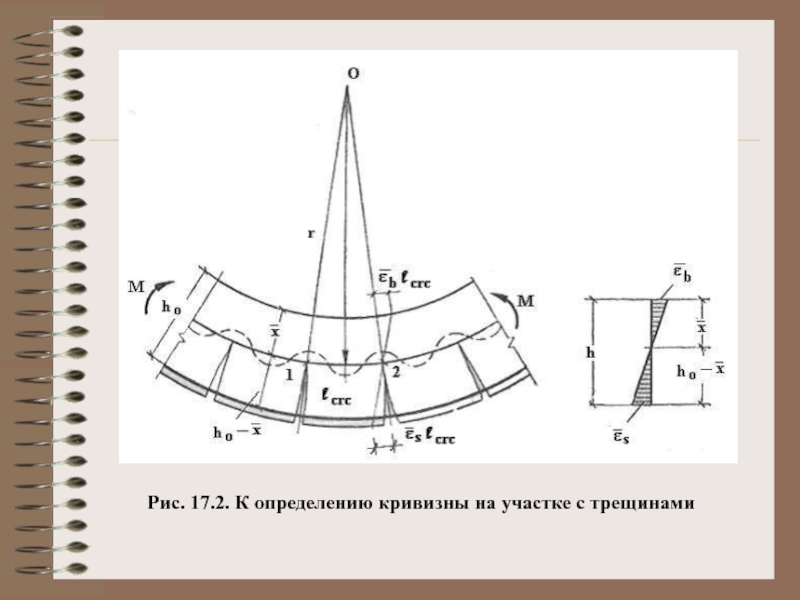
здесь εb, ε’b — относительные деформации бетона, вызванные его усадкой и ползучестью от усилия предварительного обжатия и определяемые соответственно на уровне центра тяжести растянутой продольной арматуры и крайнего сжатого волокна бетона

быстронатекающей ползучести, усадки бетона, т.е.
σ’b — принимается для напрягаемой

арматуры на уровне край­него сжатого волокна бетона.

Для элементов без предварительного напряжения значения кривизны

принимают равными нулю.

зоне.
На участках, где образуются нормальные

к продольной оси элемента трещины в стадии II ,общее деформированное состояние определяют средними деформациями растянутой арматуры , средними деформациями бетона сжатой зоны и средним положением нейтральной оси с радиусом кривизны r.
Из подобия треугольников на рисунке 17.2 получаем:

),
получаем:
В общем случае на

участках, где в растянутой зоне образуются нормальные к продольной оси элемента трещины, кривизна изгибаемых, внецентренно сжатых, а также внецентренно растянутых при элементов прямоугольного, таврового и двутаврового (коробчатого) сечений должна определяться по формуле:

Ntot – равнодействующая продольной силы N и усилия предварительного обжатия Р (при внецентренном растяжении сила N принимается со знаком „минус").
Для элементов, выполняемых без предваритель­ного напряжения арматуры, усилие Р допускается принимать равным нулю.
Значение ξ вычисляется по формуле (161) СНиП 2.03.01 –84*.

трещинами в растянутой зоне

должна определяться по формуле (170) СНиП

2.03.01 –84*.

где — кривизна от непродолжительного действия всей нагрузки, на которую про­изводится расчет по деформациям;

— кривизна от непродолжительного действия постоянных и длительных нагрузок;

— кривизна от продолжительного действия постоянных и длительных нагрузок;

— кривизна, обусловленная выгибом элемента вследствие усадки и ползучести бетона от усилия предварительного обжатия.

Если значения оказываются отрицательными, то они

принимаются равными нулю.