Слайд 1Мультимедийные лекции
по физике
Постоянный ток
Слайд 2Тема 3.
Классическая электронная теория проводимости
План лекции
3.1. Природа электрического тока
в проводниках.
3.2. Строение металлов.
3.3. Вывод закона Ома.
3.4. Вывод закона Джоуля
– Ленца.
3.5. Закон Видемана – Франца.
3.6. Достоинства и недостатки классической теории проводимости.
Слайд 33.1. Природа электрического тока в проводниках
Механизм проводимости металлов не вызывает
в настоящее время никаких сомнений.
Основным носителем тока в металлах
являются электроны.
Однако ранее вызывала удивление очень высокая электропроводность металлов и были поставлены соответствующие опыты по выяснению природы носителей тока в проводниках.
Слайд 4 Электронную теорию проводимости металлов создали немецкий физик П. Друде
(1863—1906) и нидерландский физик X. Лоренц.
П. Друде Х. Лоренц
Слайд 5Опыт К. Рикке (1901 г.)
Он предположил, что в кристаллической
решётке
металла некоторые атомы
могут быть частично ионизированы
на положительные ионы
и электроны.
К. Рикке
Через систему цилиндрических образцов Cu – Al – Cu в течение года пропускался электрический ток.
Cu
Cu
Al
Слайд 6Общий заряд, прошедший через эти цилиндры, достигал огромного значения (3,5106
Кл).
Никаких, даже микроскопических, следов переноса вещества не обнаружилось.
Этим
было доказано, что носителями тока не могли быть тяжёлые частицы – атомы или ионы.
Перенос заряда в металлах должен осуществляться частицами, которые являются общими для всех металлов.
Слайд 7Такими частицами могли быть открытые в 1897 г. английским физиком
Д. Томсоном (1856—1940)
электроны.
Для доказательства этого предположения необходимо было
определить знак и величину удельного заряда носителей.
Друде и Лоренц (1904 г.)
высказали мысль, что
носителями тока в металлах
являются
электроны.
Д. Томсон
Слайд 8Р. Милликен измерил удельный заряд электрона.
Он оказался равным:
Р. Милликен
Слайд 92. Опыт Стюарта и Толмена (1916 г.)
Идея опытов по
определению удельного заряда носителей тока в металлах заключалась в следующем.
Если в металле имеются подвижные, слабо связанные с решеткой носители тока, то при резком торможении проводника эти частицы должны по инерции смещаться вперед, как смещаются вперед пассажиры, стоящие в вагоне при его торможении.
металл
а
торможение
+
+
+
+
Слайд 10Идея этих опытов (1913) и их качественное воплощение принадлежат российским
физикам С. Л. Мандельштаму (1879—1944) и Н. Д. Папалекси (1880—1947).
Катушка из металлической проволоки, соединённая с телефоном, приводилась во вращение.
При резкой остановки катушки
в последней появлялся треск
из-за возникшей разности
потенциалов.
С. Мандельштам
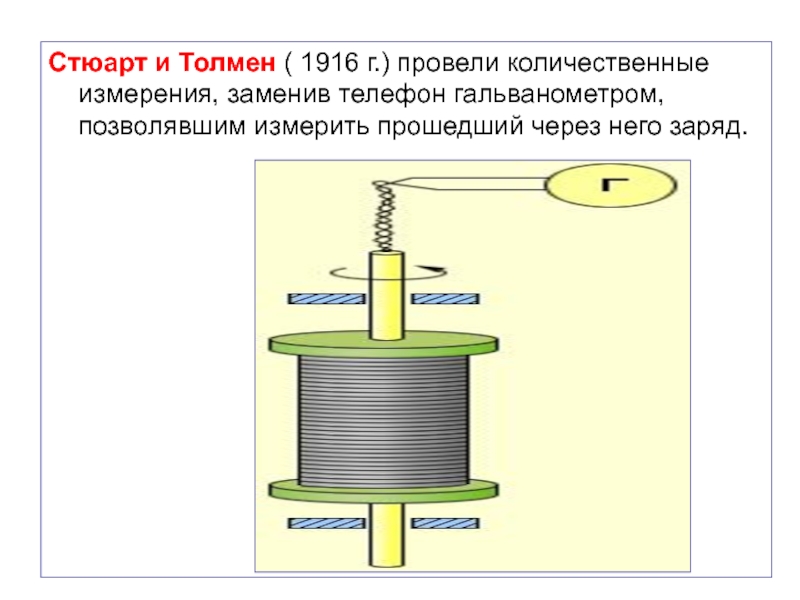
Слайд 11Стюарт и Толмен ( 1916 г.) провели количественные измерения, заменив
телефон гальванометром, позволявшим измерить прошедший через него заряд.
Слайд 13При торможении импульс электрона изменяется от своего максимального значения до
нуля.
На основе второго закона Ньютона: изменение импульса электрона равно импульсу
силы.
Силу заменим через напряжённость электрического поля, возникшего в катушке при резком торможении.
Электрическое поле в проводнике – однородное:
Слайд 14Разность потенциалов (напряжение) по закону Ома:
Сила тока:
Сделаем подстановку промежуточных формул
в первую формулу.
При торможении проводника его скорость изменяется от максимального
значения v до нуля, а заряд от нуля до Q, измеренного гальванометром.
Слайд 15
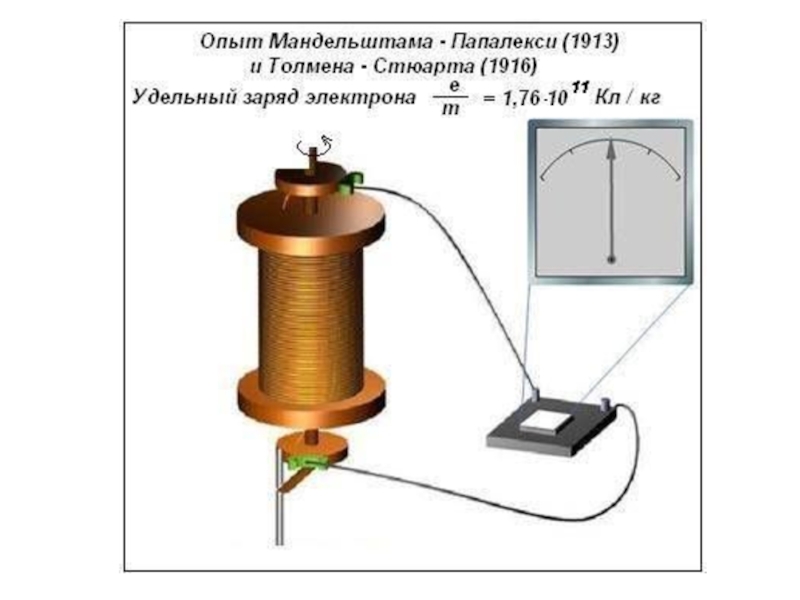
Для величины удельного заряда частицы получили значение:
Расчёты показали, что отношение
e/m = 1,76 1011 Кл/кг.
Эта величина соответствует удельному заряду
электрона.
Так было окончательно установлено, что носителями тока в металлах являются электроны.
Слайд 163.2. Строение металлов
К металлам относятся вещества, у которых один или
два валентных электрона.
При сближении атомов до расстояний порядка нанометров
образуется кристалл.
При этом электронные оболочки деформируются и перекрываются между собой.
Слайд 17Валентные электроны, находящиеся на внешних оболочках атомов, в кристалле могут
перемещаться от одного атома к другому так, что даже нельзя
сказать какому атому они принадлежат.
Такая коллективизация валентных электронов приводит к тому, что они образуют так называемый электронный газ.
Концентрация электронов в нём достаточно высока:
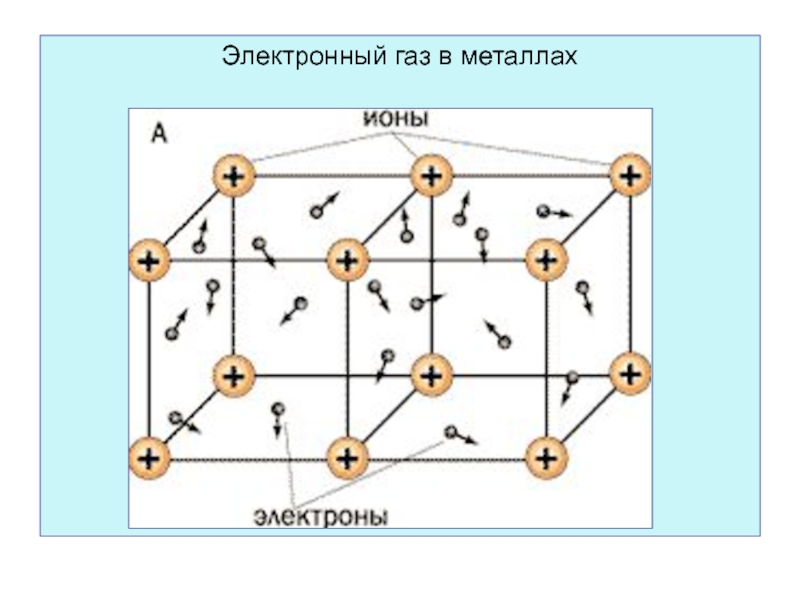
Слайд 19Металл представляет собой кристаллическую решётку из положительных ионов и электронного
газа.
= +
Электронный газ в первом приближении ведёт себя как идеальный газ.
В промежутках между столкновениями электроны движутся свободно.
В отличие от идеального газа они сталкиваются в основном не между собой, а с ионами решётки, что
приводит к установлению равновесия между электронами и решёткой.
Металл
Крист. решётка
Электр. газ
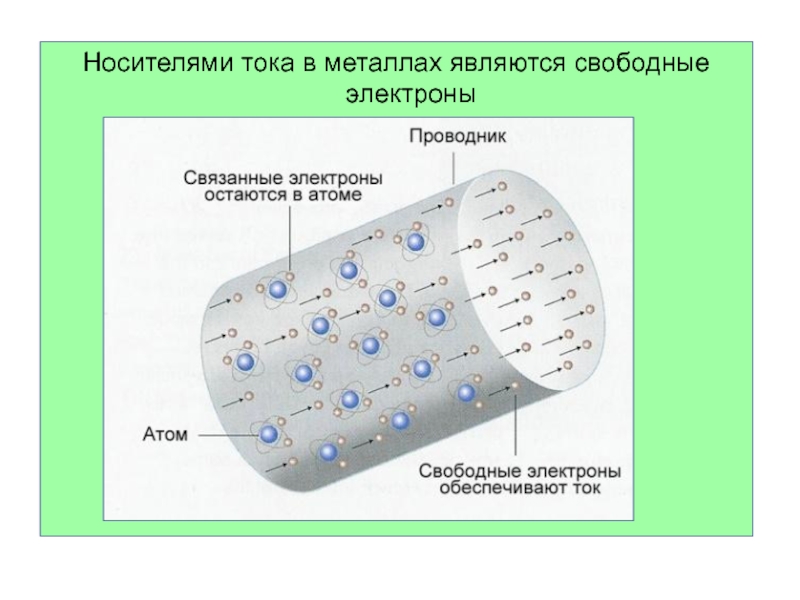
Слайд 20Носителями тока в металлах являются свободные электроны
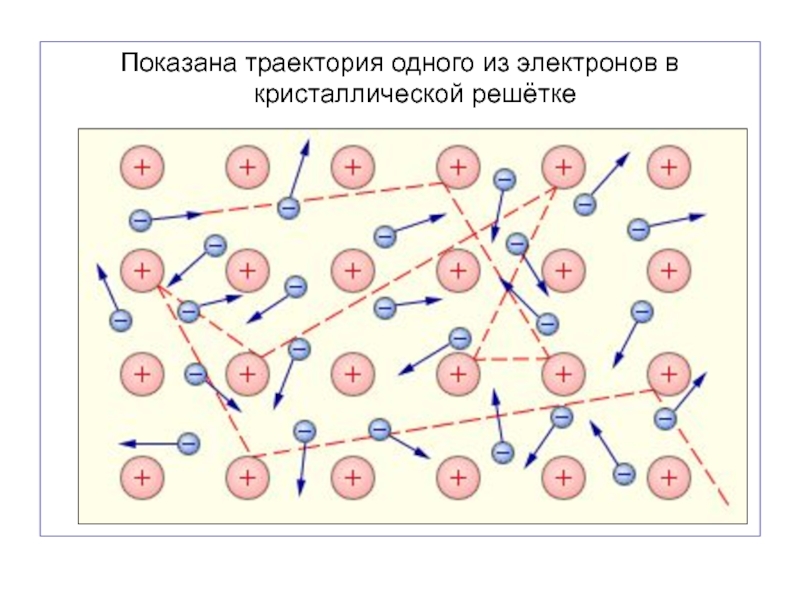
Слайд 21Показана траектория одного из электронов в кристаллической решётке
Слайд 22Вычислим среднюю арифметическую скорость свободного электрона в металле при комнатной
температуре, исходя из законов идеального газа.
Сравним: для молекул воздуха она
равна 500 м/с.
Тепловое движение электронов, являясь хаотическим, не может привести к возникновению тока.
Ток в металлах обусловлен движением свободных электронов под действием электрического поля.
Плотность тока связана со скоростью направленного движения электронов.
оценим скорость
направленного движения.
При плотности тока в
медном проводнике j = 10 А/мм2 = 107 А/м2 и концентрации электронов 1023 см-3
Вывод: скорость хаотического движения электронов во много раз больше скорости направленного движения (скорости отличаются на несколько порядков).
Слайд 24Таким образов в цепи постоянного тока электроны вдоль проводника движутся
довольно медленно.
Если же ток переменный, то за первую половину
периода электроны успевают сдвинуться на сотую долю миллиметра, а за вторую – возвратиться назад.
Так с какой же скоростью распространяется электрический ток в проводнике?
Направленное движение электронов возбуждает электромагнитная волна, скорость распространения которой равна скорости света.
Электроны металла совершают колебательные движения в поле электромагнитной волны.
Слайд 253.3. Вывод закона Ома
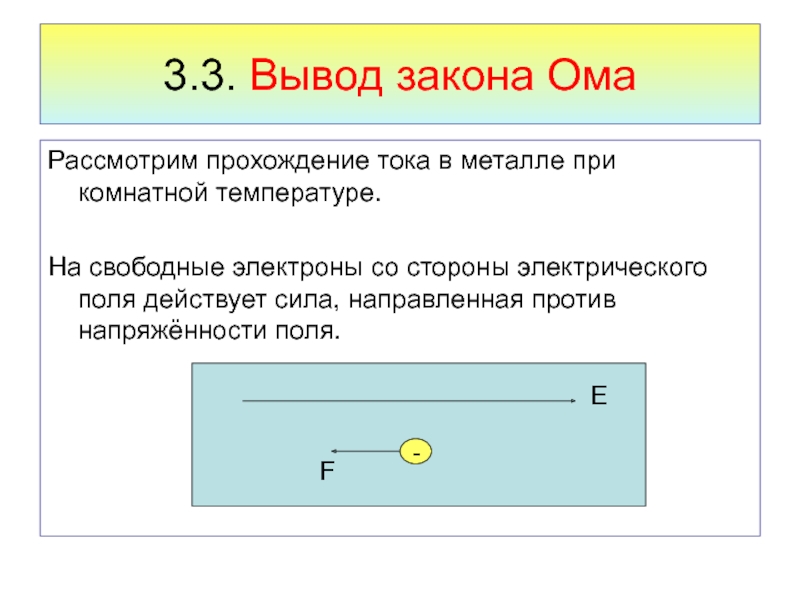
Рассмотрим прохождение тока в металле при комнатной
температуре.
На свободные электроны со стороны электрического поля действует сила, направленная
против напряжённости поля.
-
F
E
Слайд 26Под действием электрического поля электрон между двумя столкновениями с решёткой
движется равноускоренно.
Скорость его направленного движения увеличивается от нуля до максимального
значения umax в течение времени свободного пробега .
Среднее значение скорости направленного движения:
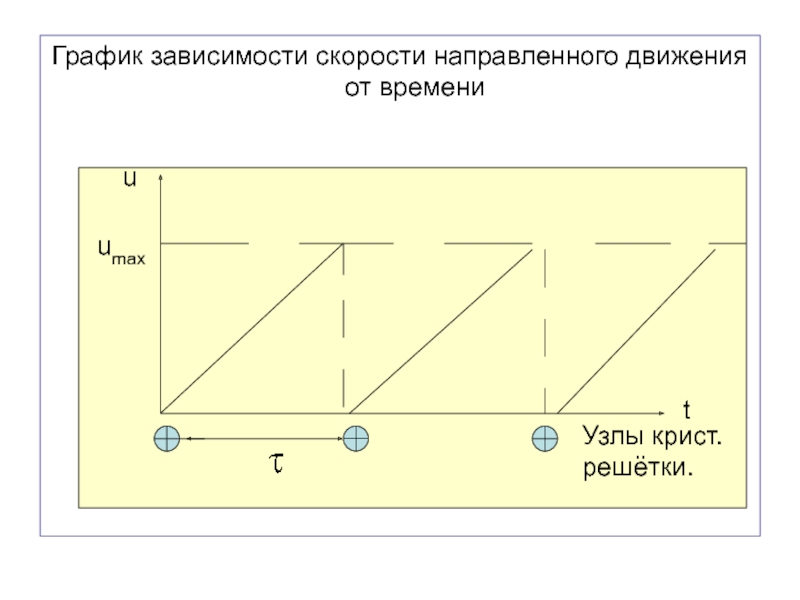
Слайд 27График зависимости скорости направленного движения от времени
t
u
umax
Узлы крист.
решётки.
Слайд 28Ускорение электрона:
Среднее время между двумя столкновениями с узлами решётки:
- средняя длина свободного пробега электрона.
Заметим, что
направленного движения много меньше скорости теплового движения .
Тогда
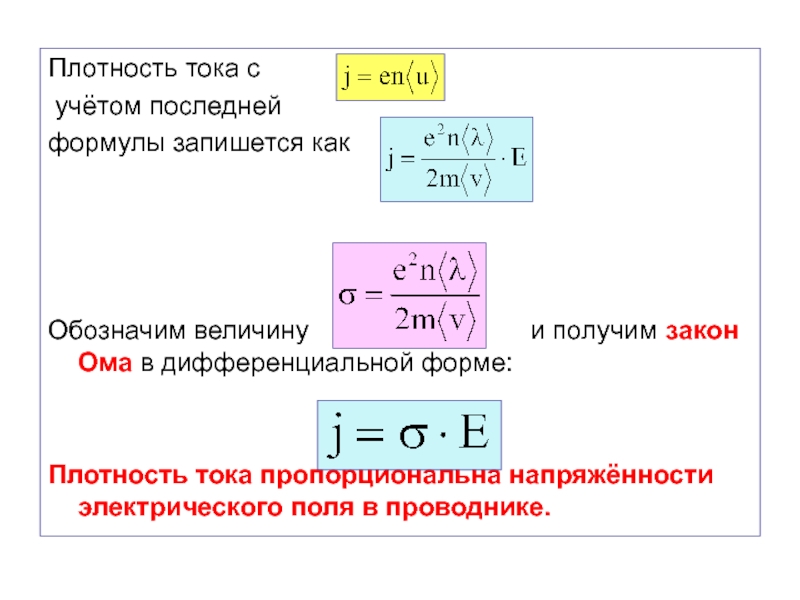
Слайд 29Плотность тока с
учётом последней
формулы запишется как
Обозначим величину
и получим закон Ома в дифференциальной форме:
Плотность тока пропорциональна напряжённости электрического поля в проводнике.
Слайд 30Классическая электронная теория позволила проводимость металла связать с параметрами электронов:
концентрацией и длиной свободного пробега.
При сравнении разных металлов проводимость такого
металла больше, у которого:
- выше валентность;
- больше межатомное расстояние (параметр кристаллической решётки).
Слайд 313.4. Вывод закона Джоуля – Ленца
Перед столкновением с узлом кристаллической
решётки электрон имеет кинетическую энергию, полученную в электрическом поле проводника.
Эта
энергия передаётся кристаллической решётке, которая нагревается.
Слайд 32Энергия, выделяемая в единицу времени в единице объёма металла, определится
как произведение величин.
n - концентрация электронов;
z – число столкновений одного
электрона с узлами кристаллической решётки;
ЕК – кинетическая энергия, полученная электроном при одном столкновении с узлом решётки.
Слайд 33Получен закон Джоуля – Ленца в дифференциальной форме.
Плотность электрической мощности
прямо пропорциональна квадрату напряжённости электрического поля в проводнике.
Из практики известно,
что кроме хорошей электропроводности металлы обладают очень хорошей теплопроводностью.
Слайд 343.5. Закон Видемана - Франца
Перенос заряда осуществляется при наличии градиента
потенциала:
Перенос теплоты осуществляется при наличии градиента температуры:
Слайд 35Поскольку перенос заряда и тепла осуществляется электронами, значит между удельной
электропроводностью (проводимостью)
и коэффициентом теплопроводности должна существовать связь.
Слайд 36Поскольку электронный газ подчиняется законам идеального газа, то удельная теплоёмкость
при постоянном объёме определяется как
Тогда коэффициент теплопроводности:
Слайд 37Отношение коэффициента теплопроводности к удельной электропроводности равно:
Заменим величину
и окончательно
получим
Слайд 38Закон Видемана – Франца (1853 г.): для всех металлов при
постоянной температуре отношение удельной теплопроводности к удельной электропроводности есть величина
постоянная, пропорциональная температуре.
Постоянная величина
е – заряд электрона;
k – постоянная Больцмана.
Слайд 393.6. Достоинства и недостатки классической теории проводимости
Достоинство:
теория позволила сделать правильные
выводы о законах постоянного тока (законах Ома, Джоуля -Ленца и
Видемана Франца).
Недостатки:
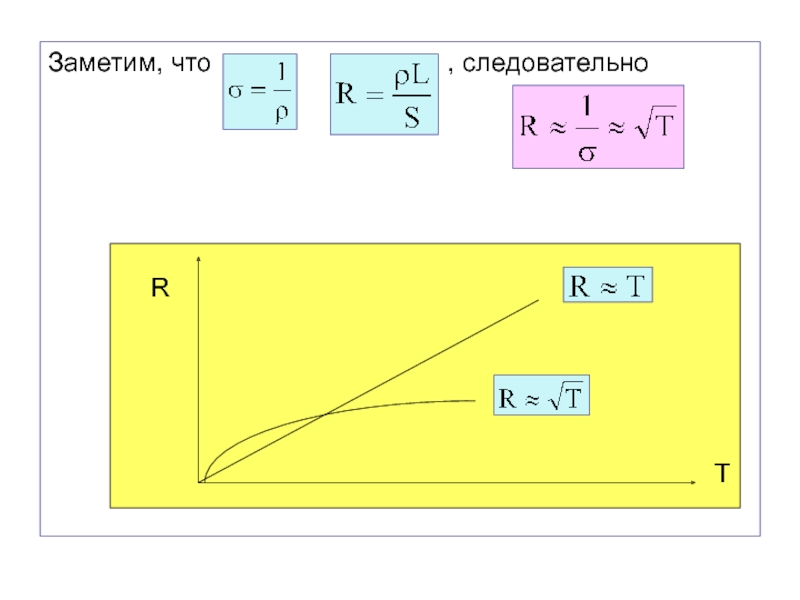
1. Теория неправильно объясняет температурную зависимость сопротивления металлов.
Слайд 40Опыты установили, что сопротивление металлов при нагревании возрастает прямо пропорционально
температуре:
По электронной теории:
Доказательство: величина проводимости может зависеть от температуры
через величину средней арифметической скорости:
Но , значит
Слайд 422. Теория даёт неправильное значение теплоёмкости металлов.
Согласно теории теплоёмкость металла
складывается из теплоёмкости кристаллической решётки (решёточная теплоёмкость) и теплоёмкости электронного
газа (электронная теплоёмкость):
Опытная теплоёмкость металлов, как и всех твёрдых тел, при комнатной температуре равна
Слайд 433. В законе Видемана –Франца теория даёт неправильный коэффициент, стоящий
перед температурой.
Произведённые Лоренцем точные расчёты с учётом максвелловского распределения электронов
по скоростям привели к замене множителя «3» на множитель «2».
Слайд 444. Электронная теория проводимости предполагает, что электроны свободно пробегают лишь
расстояния между соседними узлами кристаллической решётки.
Опыт показывает, что электроны свободно
пробегают в десятки и сотни раз большие расстояния.
Это сказывается на теплоёмкости электронного газа: она оказывается пренебрежительно малой по сравнению с решёточной теплоёмкостью.
Слайд 45Серьёзные затруднения, которые испытывает кл. эл. теория проводимости, свидетельствуют о
том, что эта теория не учитывает некоторые специфические свойства свободных
электронов.
Эти свойства учитывает квантовая теория металлов, в основе которой лежат принципиально новые идеи:
корпускулярно-волновой дуализм природы электронов;
дискретности значений полной энергии электронов;
неразличимости электронов в металле;
учёт принципа Паули.