Слайд 1Мультимедийные лекции по физике
Электростатика
Слайд 2Тема 4. Электростатическое поле в проводниках
План лекции
4.1. Распределение внешнего заряда
на проводнике.
4.2. Проводник во внешнем электростатическом поле.
4.3. Электроёмкость проводников и
конденсаторов.
4.4. Соединение конденсаторов в батарею.
Слайд 34.1. Распределение внешнего заряда на проводнике
Все вещества природы делятся на
проводники, полупроводники и диэлектрики по способности проводить электрический ток.
В
обычных условиях проводники очень хорошо проводят электрический ток.
К проводникам относятся металлы, электролиты, расплавы, ионизированные газы, плазма и т. д.
Полупроводники не проводят электрический ток, но их проводимость начинает возрастать при нагревании или внесении примесей.
Слайд 4К полупроводникам относятся элементы IV группы таблицы Д. И. Менделеева
(кремний, германий), арсенид галлия и многие химические соединения.
Диэлектрики – вещества,
плохо проводящие электрический ток, так как свободных носителей зарядов в них практически нет.
При не очень высоких температурах и не очень сильных полях диэлектрики проводят ток в
раз хуже, чем проводники.
Диэлектриками являются газы при обычных условиях, многие чистые жидкости, слюда, фарфор, мрамор и др.
Слайд 5По своему внутреннему строению проводники имеют кристаллическую решетку, в узлах
которой находятся положительные атомные остатки и электронный газ с очень
высокой концентрацией свободных электронов:
n1020-1023 электронов/см3.
Отрицательный заряд свободных электронов равен положительному заряду решетки и поэтому металлическое тело (проводник) – электрически нейтрально.
Слайд 61. Внешний заряд величиной q, равномерно распределяется по поверхности проводника.
2. Условие равновесия зарядов требует, чтобы напряженность электрического поля внутри
проводника была равна нулю (Е = 0).
Слайд 7Это вытекает из закона сохранения энергии.
Если бы выполнялось условие
Е ≠ 0, то в проводнике протекал бы ток без дополнительных источников
энергии.
На основании формулы связи напряженности с потенциалом (Е = -d /dr) следует, что при равенстве величины Е нулю, потенциал должен быть величиной постоянной: = const.
3. Поверхность, и объем проводника являются эквипотенциальными.
Заряженное металлическое тело является эквипотенциальной областью.
Слайд 84. Заряженный проводник – источник электрического поля.
Силовые линии этого
поля идут перпендикулярно его поверхности (силовые линии напряжённости перпендикулярны эквипотенциальным
линиям).
Слайд 9 Представим вектор напряжённости внешнего поля
в виде двух составляющих.
При этом
и = 0.
Действительно, если бы ≠ 0, то это вызвало бы движение зарядов по поверхности проводника и равновесие зарядов отсутствовало бы.
En
E
+
+
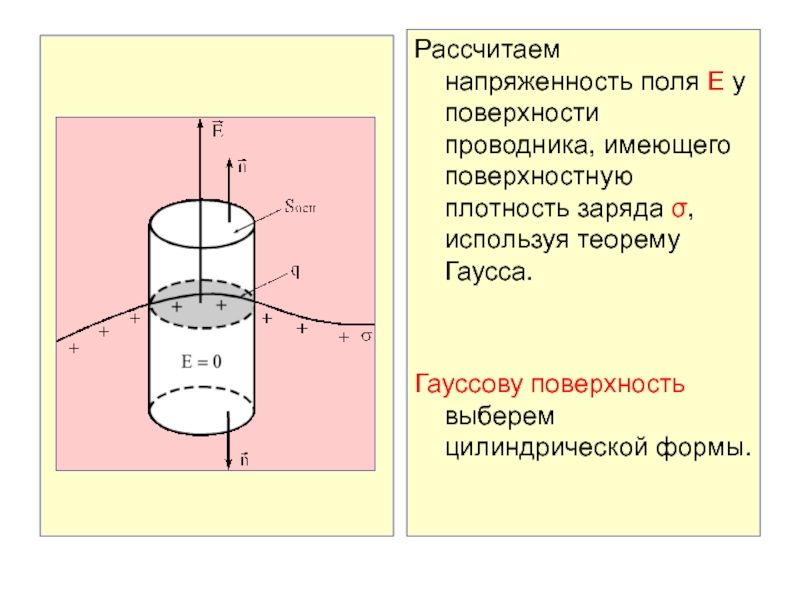
Слайд 10Рассчитаем напряженность поля Е у поверхности проводника, имеющего поверхностную плотность
заряда , используя теорему Гаусса.
Гауссову поверхность выберем цилиндрической формы.
Слайд 12Поток вектора напряжённости через воображаемую цилиндрическую замкнутую поверхность N найдем
как сумму потоков через ее боковую поверхность, нижнее и верхнее
основания:
Нормаль к основанию параллельна силовым линиям , поэтому Еn = Е, где Еn – проекция вектора на нормаль к основанию цилиндрической поверхности.
В пределах основания цилиндра Sосн. поле считаем однородным.
Слайд 13Интеграл по боковой поверхности равен нулю, так как силовые линии
электрического поля её не пересекают.
Интеграл по нижнему основанию также равен
нулю, потому что поле внутри проводника отсутствует
(Е = 0).
Таким образом, остается отличным от нуля интеграл по верхнему основанию.
Слайд 14Заряд, находящийся внутри цилиндрической поверхности, расположен на поверхности проводника и
равен:
По теореме Гаусса имеем:
Тогда:
Последняя формула определяет напряжённость поля у поверхности
заряженного проводника.
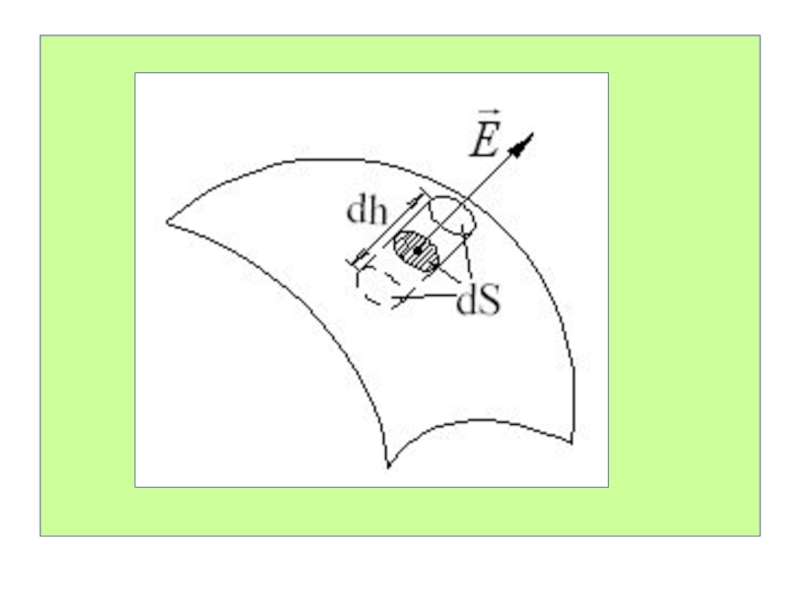
Слайд 15Чем больше поверхностная плотность заряда на поверхности проводника, тем большую
напряженность поля он создает вблизи поверхности.
Величина поверхностной плотности заряда
определяется радиусом кривизны поверхности r: чем меньше r, тем больше , тем больше Е.
Е
Слайд 16В местах проводника с малым радиусом кривизны поверхности (особенно остриях)
может возникнуть сильное электрическое поле.
При напряженности поля порядка 30 В/см
оно способно ионизовать воздух.
Вблизи острия возникнут свободные заряды.
Возникает явление, называемое стеканием зарядов с проводника.
Процесс ионизации воздуха сопровождается его свечением (огни святого Эльма вокруг мачт на кораблях).
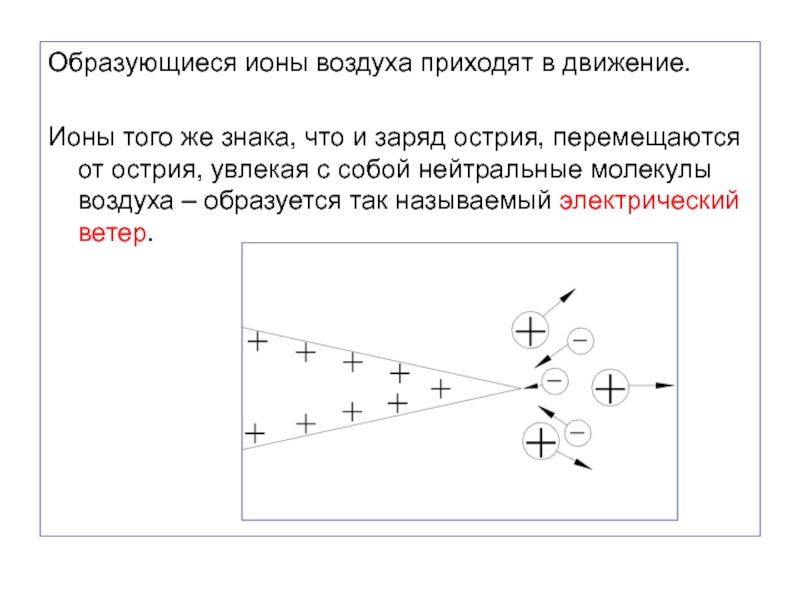
Слайд 17Образующиеся ионы воздуха приходят в движение.
Ионы того же знака,
что и заряд острия, перемещаются от острия, увлекая с собой
нейтральные молекулы воздуха – образуется так называемый электрический ветер.
Слайд 18Ионы противоположенного знака идут к острию, частично нейтрализуя его заряд
и ослабляя поле.
На этом явлении основано действие молниеотвода.
Процесс
ионизации воздуха сопровождается его свечением (огни святого Эльма вокруг мачт на кораблях).
Слайд 19Так как избыточные заряды располагаются только по внешней поверхности проводника,
то наличие в нем внутренних полостей не влияет на характер
этого распределения.
Равновесное распределение зарядов на сплошном проводнике такое же, как и на полом, при условии одинаковости их внешней формы.
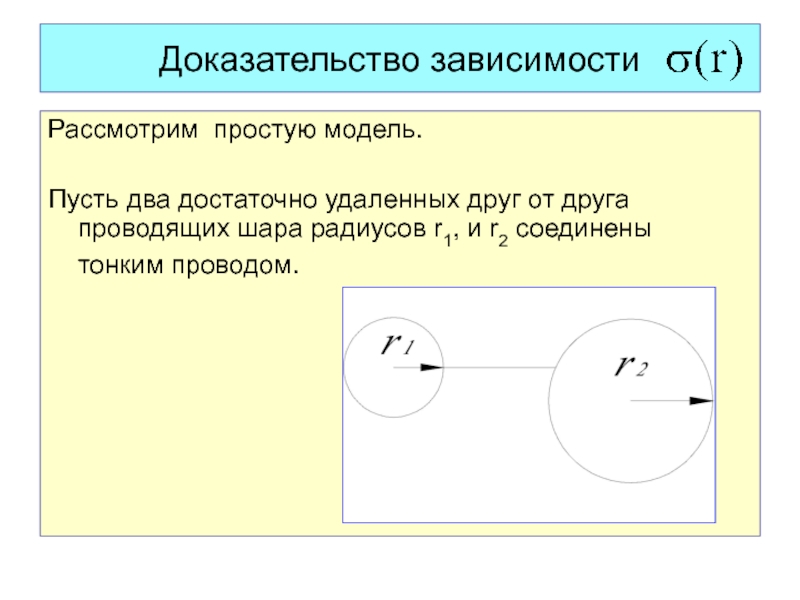
Слайд 20Рассмотрим простую модель.
Пусть два достаточно удаленных друг от друга
проводящих шара радиусов r1, и r2 соединены тонким проводом.
Доказательство
зависимости
Слайд 21Если сообщить одному из шаров некоторый заряд q, то он
растечется по внешней поверхности шаров и проводника так, что потенциалы
шаров окажутся равными: φ1 = φ2
Так как шары достаточно удалены и полем провода можно пренебречь, то потенциалы шаров можно вычислять по формуле:
Тогда
Слайд 22 Выразим величину заряда через поверхностную плотность заряда:
Тогда
Поверхностная плотность зарядов
в отдельных точках проводника тем больше, чем больше кривизна поверхности.
r
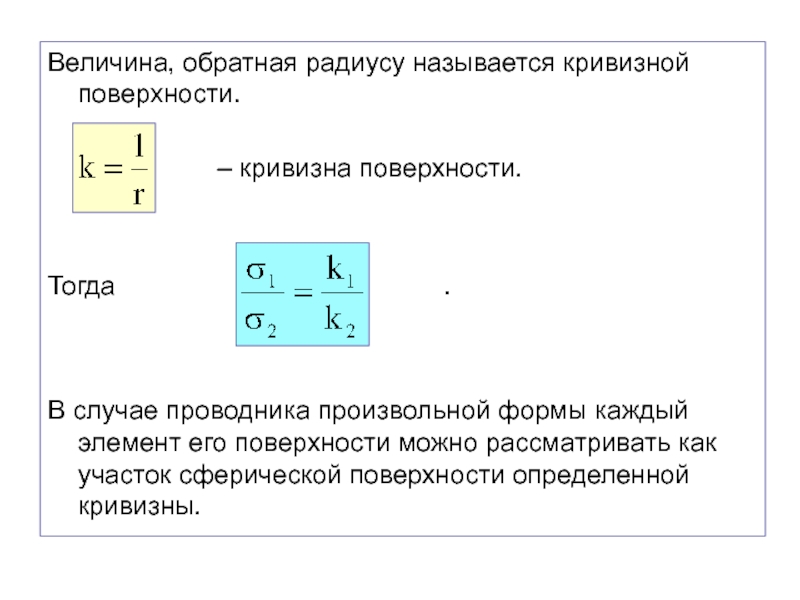
Слайд 23Величина, обратная радиусу называется кривизной поверхности.
– кривизна поверхности.
Тогда .
В случае проводника произвольной формы каждый элемент его поверхности можно рассматривать как участок сферической поверхности определенной кривизны.
Слайд 24 4.2. Проводник во внешнем электрическом поле
Если незаряженный проводник внести
в однородное электрическое поле напряженностью , то электроны проводника
придут в направленное движение против силовых линий внешнего поля и соберутся на одном из его концов.
Другой конец проводника зарядится положительно, так как количество электронов здесь уменьшится.
1.Внешнее электрическое поле разделяет заряды самого проводника.
Слайд 25Электростатическая индукция
Электростатическая индукция - явление перераспределения зарядов внутри проводника под
действием внешнего электрического поля.
Это наблюдается при любых напряженностях внешнего поля.
Индуцированными зарядами называются избыточные заряды, скопившиеся на разных концах проводника.
Слайд 26Индуцированные заряды создают внутри проводника свое собственное поле напряжённостью
, противоположно направленное
внешнему полю ЕО.
2. Процесс перераспределения зарядов прекратится при условии равенства напряженности поля Е' индуцированных зарядов и напряженности ЕО
внешнего поля: Е' = Е0.
Суммарная напряжённость внутри проводника:
Слайд 273. Суммарная напряженность поля внутри проводника равна нулю: Е =
0, поскольку напряженности названных полей направлены
в разные стороны.
4. Проводник уничтожает внешнее поле там, где он находится.
5. Поверхность и все точки проводника являются эквипотенциальной областью.
Слайд 296. Вблизи проводника внешнее поле искажается.
Силовые линии внешнего поля заканчиваются
на отрицательных индуцированных зарядах проводника, и вновь начинаются на индуцированных
положительных зарядах, входя и выходя в его поверхность перпендикулярно.
7. Проводник, внесенный в электрическое поле, разрывает часть линий напряженности внешнего поля.
8. Если из сплошного проводника изъять внутреннюю часть вещества, равновесие индуцированных зарядов не нарушается.
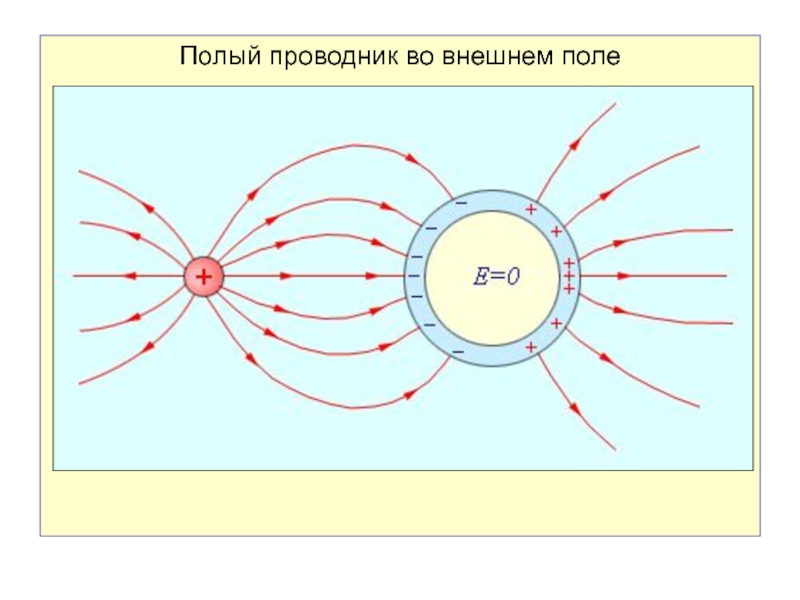
Слайд 319. Электрическое поле внутри проводника отсутствует независимо от того, сплошной
проводник или полый, так как индуцированные заряды располагаются только на
внешней поверхности проводника.
На этом основана электростатическая защита.
Когда какой-то прибор необходимо защитить от действия внешних полей, его окружают проводящим экраном.
Внешнее поле компенсируется внутри экрана возникающими на его поверхности индуцированными зарядами.
Слайд 32 Метод защиты от электрических полей
Помещают исследуемую систему с
приборами внутри металлической сетки и этим экранируют ее от действия
внешних электрических полей.
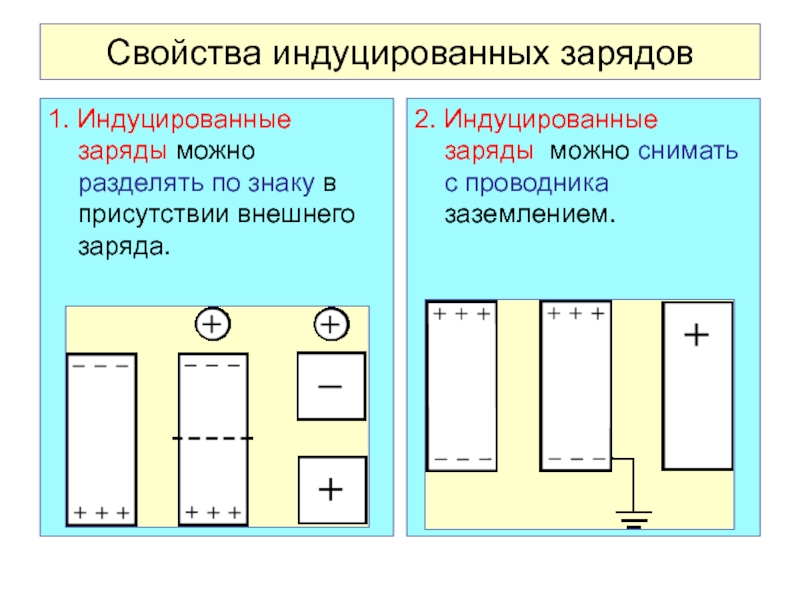
Слайд 33Свойства индуцированных зарядов
1. Индуцированные заряды можно разделять по знаку в
присутствии внешнего заряда.
2. Индуцированные заряды можно снимать с проводника заземлением.
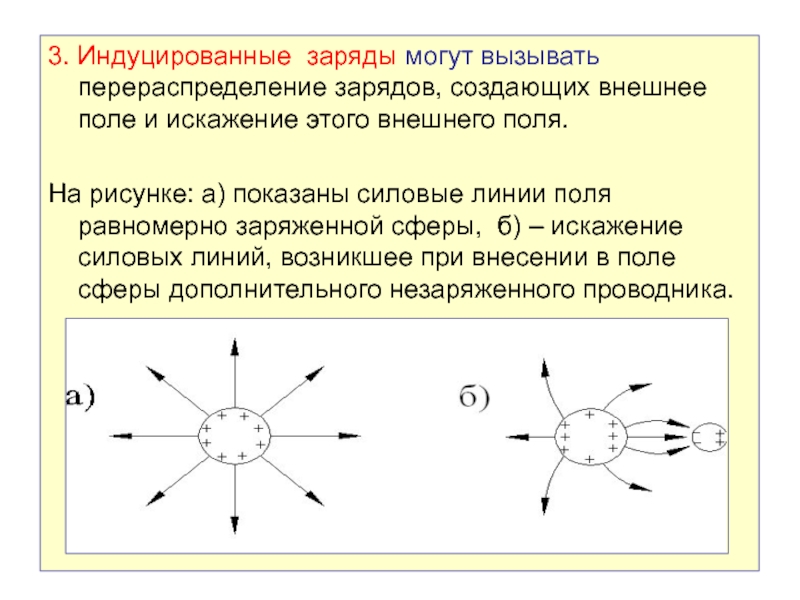
Слайд 343. Индуцированные заряды могут вызывать перераспределение зарядов, создающих внешнее поле
и искажение этого внешнего поля.
На рисунке: а) показаны силовые
линии поля равномерно заряженной сферы, б) – искажение силовых линий, возникшее при внесении в поле сферы дополнительного незаряженного проводника.
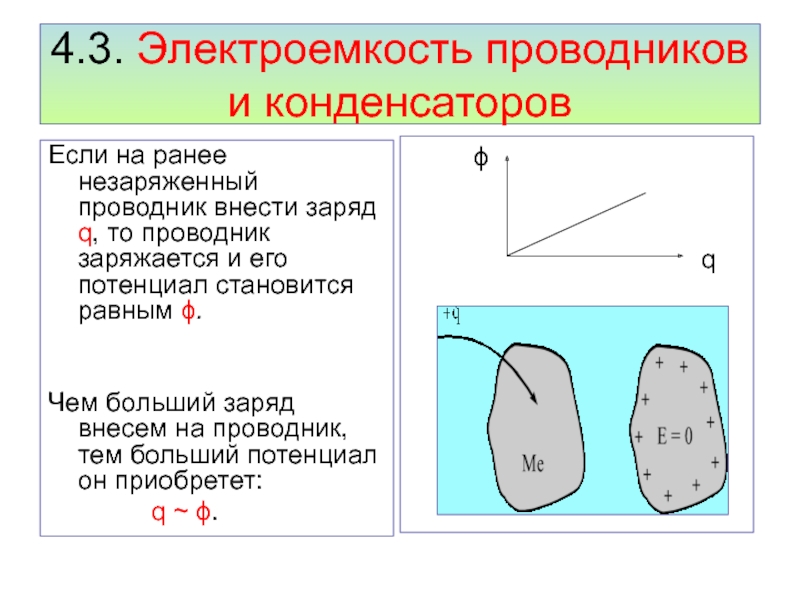
Слайд 354.3. Электроемкость проводников и конденсаторов
Если на ранее незаряженный проводник внести
заряд q, то проводник заряжается и его потенциал становится равным
.
Чем больший заряд внесем на проводник, тем больший потенциал он приобретет:
q .
q
Слайд 36Величиной, определяющей функциональную зависимость между зарядом проводника и его потенциалом,
является электроемкость С.
Для электроемкости можно записать ряд формул, из которых
следует физический смысл этой величины:
Электроемкость численно равна заряду, который изменяет потенциал проводника на единицу.
Слайд 37Электроёмкость:
- измеряется в фарадах: [C] = 1 Ф (Ф =
Кл/В);
- характеристика самого проводника;
- не зависит ни от его заряда,
ни от потенциала;
- определяется формой, размерами проводника;
зависит от диэлектрических свойств окружающей среды ( ).
Вычислим электроемкость:
шара;
плоского конденсатора.
Слайд 38Электроёмкость шара
Потенциал шара определяется по формуле потенциала точечного заряда:
где R
– радиус шара, коэффициент
.
Тогда:
С
R
R
q
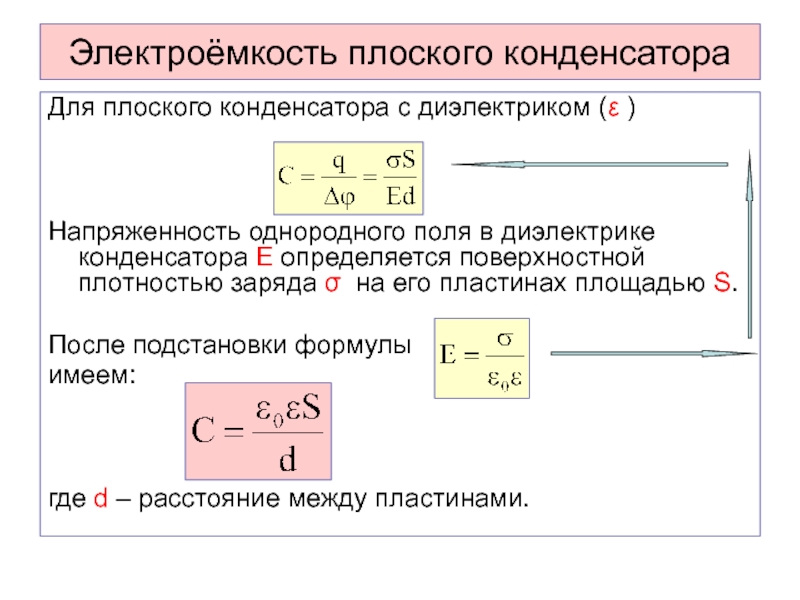
Слайд 39Электроёмкость плоского конденсатора
Для плоского конденсатора с диэлектриком ( )
Напряженность однородного
поля в диэлектрике конденсатора E определяется поверхностной плотностью заряда
на его пластинах площадью S.
После подстановки формулы
имеем:
где d – расстояние между пластинами.
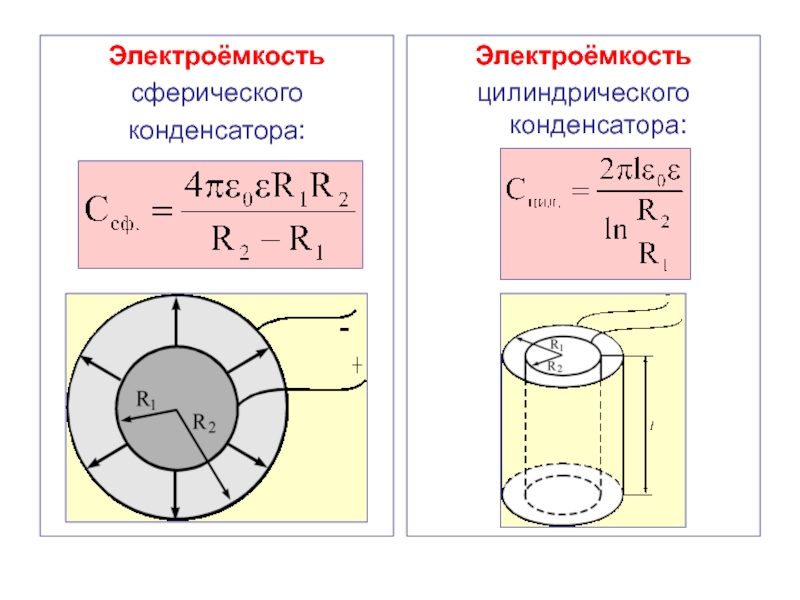
Слайд 40Электроёмкость
сферического
конденсатора:
Электроёмкость
цилиндрического конденсатора:
Слайд 41Соединение конденсаторов в батарею
Для получения необходимой емкости конденсаторы соединяют
между собой в батареи.
Батарея конденсаторов – несколько соединенных друг с
другом конденсаторов.
Заряд батареи – заряд, который проходит по проводнику, соединяющему положительный и отрицательный полюсы батареи.
Электроёмкость батареи – величина, численно равная отношению заряда батареи и абсолютной величине разности потенциалов, между полюсами батареи.
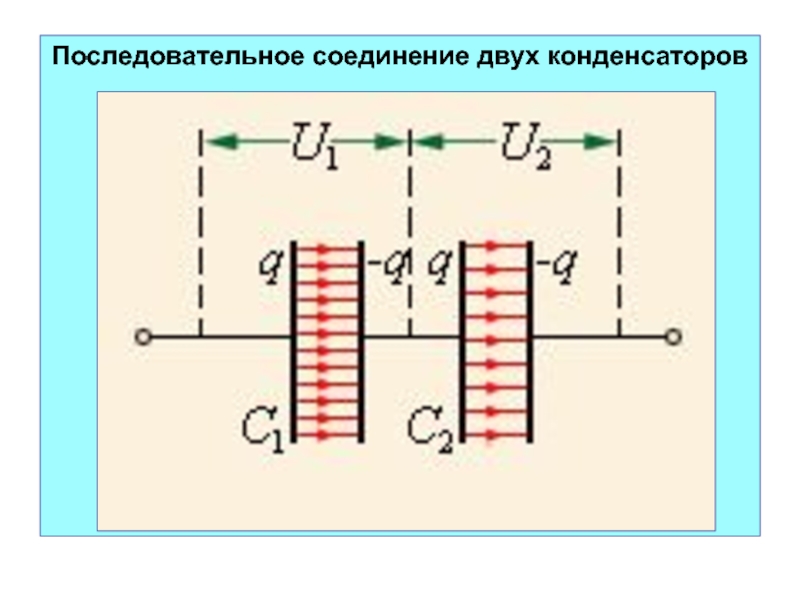
Слайд 42Последовательное соединение двух конденсаторов
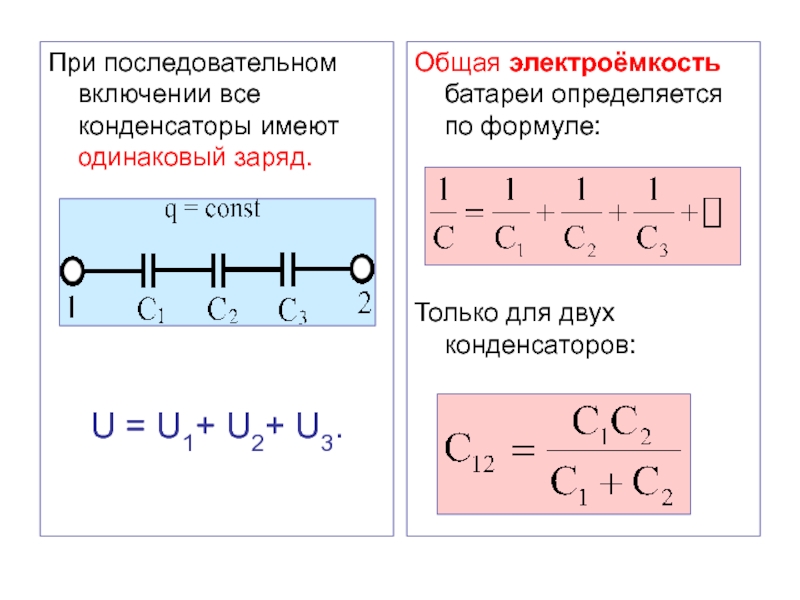
Слайд 43При последовательном включении все конденсаторы имеют одинаковый заряд.
U =
U1+ U2+ U3.
Общая электроёмкость батареи определяется по формуле:
Только для двух конденсаторов:
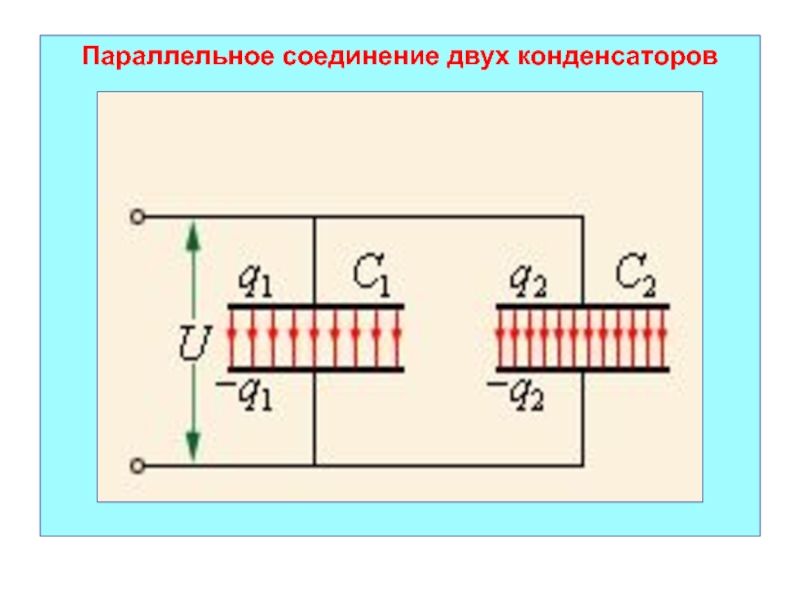
Слайд 44Параллельное соединение двух конденсаторов
Слайд 45
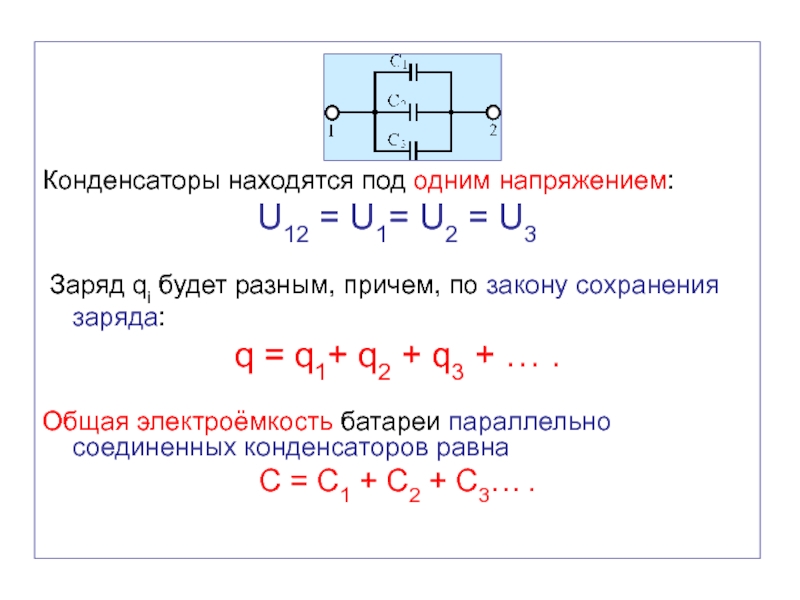
Конденсаторы находятся под одним напряжением:
U12 = U1= U2 =
U3
Заряд qi будет разным, причем, по закону сохранения
заряда:
q = q1+ q2 + q3 + .
Общая электроёмкость батареи параллельно соединенных конденсаторов равна
С = С1 + С2 + С3 .


























![Мультимедийные лекции по физике Электроёмкость:- измеряется в фарадах: [C] = 1 Ф (Ф = Кл/В);- Электроёмкость:- измеряется в фарадах: [C] = 1 Ф (Ф = Кл/В);- характеристика самого проводника;- не зависит ни](/img/thumbs/e9383da7bc8302cbce39b04508628691-800x.jpg)