Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Мы щелкаем задачи по теории вероятностей как орешки
Содержание
- 1. Мы щелкаем задачи по теории вероятностей как орешки
- 2. ОпределенияОпределение: Событие, которое может произойти, а может
- 3. ОпределенияСобытие Ā называется противоположным событию А, если
- 4. Классическое определение вероятности:
- 5. Классическое определение вероятности:Пример.Андрей, Роман, Максим и Сергей
- 6. Вероятность события А равна сумме вероятностей элементарных
- 7. ОпределенияВероятность противоположных событий:Р(А) + Р(Ā) = 1Р(А)
- 8. Формулы сложения и умножения вероятностейФормула сложения вероятностей
- 9. ФакториалОпределение: Факториалом числа n называется произведение первых
- 10. Сочетания
- 11. Пример на сочетания
- 12. Формула Бернулли:
- 13. Тип 1. Самая простая задача
- 14. Тип 2. Задача с бросанием монет
- 15. Тип 2. Задача с бросанием монет
- 16. Тип 2. Задача с бросанием монет
- 17. Тип 3. Задача с игральным кубиком
- 18. Тип 4. Задача с игральными костями
- 19. Тип 4. Задача с игральными костямиДля решения данного типа удобно использовать следующую таблицу:
- 20. Тип 4. Задача с игральными костями
- 21. Тип 5. Задача с перекладыванием монет
- 22. Тип 6. Задача с экзаменационными билетамиНа экзамене
- 23. Тип 7. Задача с кофейными автоматамиВ торговом
- 24. Тип 8. Задача о стрельбе по мишенямБиатлонист
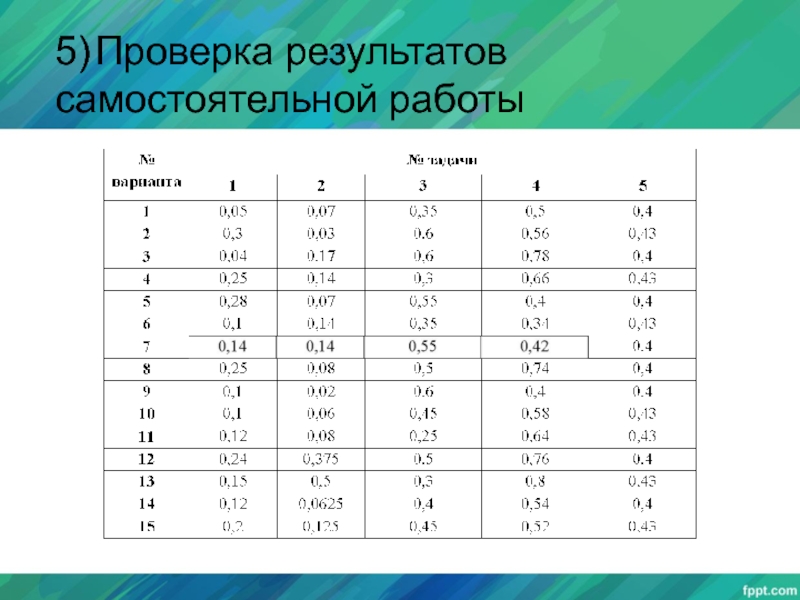
- 25. 5) Проверка результатов самостоятельной работы
- 26. Домашнее задание:Повторить всю теорию по теме.Проанализировать алгоритмы
- 27. Скачать презентанцию
ОпределенияОпределение: Событие, которое может произойти, а может и не произойти, называют случайным событием.Пример: Попадание или промах при стрельбе по мишени.Элементарные события – простейшие события (исходы), которыми может окончиться случайный опыт.
Слайды и текст этой презентации
Слайд 2Определения
Определение: Событие, которое может произойти, а может и не произойти,
называют случайным событием.
события – простейшие события (исходы), которыми может окончиться случайный опыт.Слайд 3Определения
Событие Ā называется противоположным событию А,
если состоит из тех
и только тех элементарных исходов,
которые не входят в А.
Два
случайных события называются несовместными, если они не могут произойти одновременно при одном
и том же исходе испытания.
Слайд 5Классическое определение вероятности:
Пример.
Андрей, Роман, Максим и Сергей бросили жребий, кому
быть вратарем.
Найти вероятность того, что вратарем стал Роман.
Решение:
Пусть событие
А = {вратарем стал Роман}.Число благоприятных исходов k = 1.
Общее число возможных исходов n = 4.
По формуле классической вероятности получаем:
P(A) = = 0, 25.
Ответ: 0,25
Слайд 6Вероятность события А равна сумме вероятностей элементарных событий, благоприятствующих этому
событию.
Сумма вероятностей всех элементарных событий равна 1.
В задании №4
ЕГЭ по математике ответ всегда записывается в виде положительной десятичной дроби, значение которой всегда меньше 1.Слайд 7Определения
Вероятность противоположных событий:
Р(А) + Р(Ā) = 1
Р(А) = 1 -
Р(Ā)
AU B (объединение) – событие, состоящее из элементарных исходов, благоприятствующих
хотя бы одному из событий А, В.А ∩ В (пересечение) – событие, состоящее из элементарных исходов, благоприятствующих обоим событиям А и В.
Слайд 8Формулы сложения и умножения вероятностей
Формула сложения вероятностей для совместных событий:
Р(A
U B) = Р(А) + Р(В) – Р(А ∩ В)
Формула
сложения для несовместных событий:Р(A U B) = Р(А) + Р(В)
Формула умножения вероятностей для независимых событий:
Р( A ∩ B) = Р(А)*Р(В)
Формула умножения вероятностей для зависимых событий:
Р( A ∩ B) = Р(А)*Р(В\А) = Р(В)*Р(А\В)
Слайд 9Факториал
Определение: Факториалом числа n называется
произведение первых натуральных n чисел
от 1 до n.
Обозначение: n!
Формула: n! = 1*2*3*….*n
Пример: 4! =
1*2*3*4 = 24Запомните: 0! = 1 (по определению)
Слайд 19Тип 4. Задача с игральными костями
Для решения данного типа удобно
использовать следующую таблицу:
Слайд 22Тип 6. Задача с экзаменационными билетами
На экзамене по геометрии школьнику
достаётся один вопрос из списка экзаменационных вопросов. Вероятность того, что
это вопрос на тему «Вписанная окружность», равна 0,1. Вероятность того, что это вопрос на тему «Тригонометрия», равна 0,35. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.Решение:
1. А = {вопрос на тему «Вписанная окружность»}
В = {вопрос на тему «Тригонометрия»}
С = {вопрос по одной из этих двух тем}
2. События А и В несовместны, т.к. по смыслу задачи нет вопросов, относящихся к двум темам одновременно. Значит, С = A U B.
3. По правилу сложения для несовместных событий имеем:
Р (С) = Р(A U B) = Р(А) + Р(В)
Р(С) = 0,1 + 0,35 = 0,45.
Слайд 23Тип 7. Задача с кофейными автоматами
В торговом центре два одинаковых
автомата продают кофе. Вероятность того, что к концу дня в
автомате закончится кофе, равна 0,2. Вероятность того, что кофе закончится в обоих автоматах, равна 0,16. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.Решение:
1. А = {кофе закончится в первом автомате}
В = {кофе закончится во втором автомате}
С = A U B = {кофе закончится хотя бы в одном автомате}
2. По условию: Р(А) = Р(В) = 0,2, Р(А ∩ В) = 0,16
3. По смыслу задачи события А и В являются совместными. По формуле сложения вероятностей совместных событий имеем:
Р(С) = Р(A U B) = Р(А) + Р(В) – Р(А ∩ В) = 0,2 + 0,2 – 0,16 = 0,24.
4. Р( A U B) = 1 – 0,24 = 0,76.
Ответ: 0,76
Слайд 24Тип 8. Задача о стрельбе по мишеням
Биатлонист 4 раза стреляет
по мишеням. Вероятность попадания в мишень при одном выстреле равна
0,85. Найдите вероятность того, что биатлонист первые 2 раза попал в мишени, а последние два промахнулся. Результат округлите до сотых.Решение:
Вероятность попадания = 0,85.
Вероятность промаха = 1 – 0,85 = 0,15.
А = {попадание, попадание, промах, промах}
События независимые. По формуле умножения вероятностей:
Р(А) = 0,85*0,85*0,15*0,15 = 0,7225*0,0225 = 0,01625625 ≈ 0,02.
Ответ: 0,02
Слайд 26Домашнее задание:
Повторить всю теорию по теме.
Проанализировать алгоритмы решения всех ключевых
задач.
Решить в рабочих тетрадях задачи:
В случайном эксперименте симметричную монету бросают
пять раз. Найдите вероятность того, что орел выпадет ровно 4 раза. Биатлонист 5 раз стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,75. Найдите вероятность того, что биатлонист первые 4 раза попал в мишени, а последний раз промахнулся. Результат округлите до сотых.
В магазине стоят два платежных автомата. Каждый из них может быть неисправен с вероятностью 0,03 независимо от другого автомата. Найдите вероятность того, что хотя бы один автомат исправен.