Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Тригонометрия
Содержание
- 1. Тригонометрия
- 2. Возникновение науки тригонометрия
- 3. Наука об измерении треугольника,О выражении сторон через его углытригонометрия
- 4. Треугольник-это простейшая фигура, три стороны и три
- 5. Синус, косинус и тангенс острого угла прямоугольного
- 6. На рисунке изображены система координат Оxy и
- 7. Синус, косинус и тангенс угла. Введём прямоугольную
- 8. Тангенсом угла α (α≠90) называется отношение sinα
- 9. Свойства
- 10. Знаки sin a. Так как sin
- 11. Знаки cos a. Знак cos a
- 12. Знаки tg a и ctg a.
- 13. Формулы для вычисления координат точкиПусть задана система
- 14. Скачать презентанцию
Возникновение науки тригонометрия
Слайды и текст этой презентации
Слайд 1Тригонометрия.
Возникновение тригонометрии
Основное тождество
Синус, косинус и тангенс угла
Свойства синуса, косинуса и
тангенса
Слайд 4Треугольник-это простейшая фигура, три стороны и три вершины
Математики его называют
двухмерным симплексом. « симплекс» по- латыни означает простейший. Необходимость вычисления
положения звёзд, для всевозможных долгосрочных прогнозов привела к необходимости научится обращаться с углами. Дитя астрологов –сферическая геометрия- привела к созданию тригонометрии- науки о измерении треугольникаСлайд 5Синус, косинус и тангенс острого угла прямоугольного треугольника
Синусом острого
угла прямоугольного треугольника называется отношение
противолежащего катета к гипотенузе
Sin A =
BC:ABКосинусом острого угла
прямоугольного треугольника
называется отношение
прилежащего катета к гипотенузе
Cos A = AC :AB
Тангенсом острого угла
прямоугольного треугольника
называется отношение противолежащего
катета к прилежащему катету
Tg A = BC:AC
Слайд 6На рисунке изображены система координат Оxy и единичная полуокружность DСВ
с центром О. Эта полуокружность является дугой окружности, уравнение которой
имеет вид X + Y=1. Подставив сюда выражения для x u y из формулы: sin = x, cos = y, получим равенствоосновное тригонометрическое тождество
Слайд 7Синус, косинус и тангенс угла.
Введём прямоугольную систему координат Оху
и построим окружность радиуса 1 с центром в начале координат.
Назовём её единичной окружностью. Из точки О проведём луч h, пересекающий единичную окружность в точке М(х;у). Обозначим буквой α угол между лучом h и положительной полуосью абсцисс.Если угол α острый, то из прямоугольного треугольника DOM имеем sin α =MD/OM, cos α =OD/OM.
Но OM=1, MD=у, OD=х, поэтому sin α =у, cos α =х.
Таким образом, для любого угла из промежутка 0°≤ α ≤180° синусом угла α называется ордината у точки М, а косинусом угла α -абсцисса х точки М.
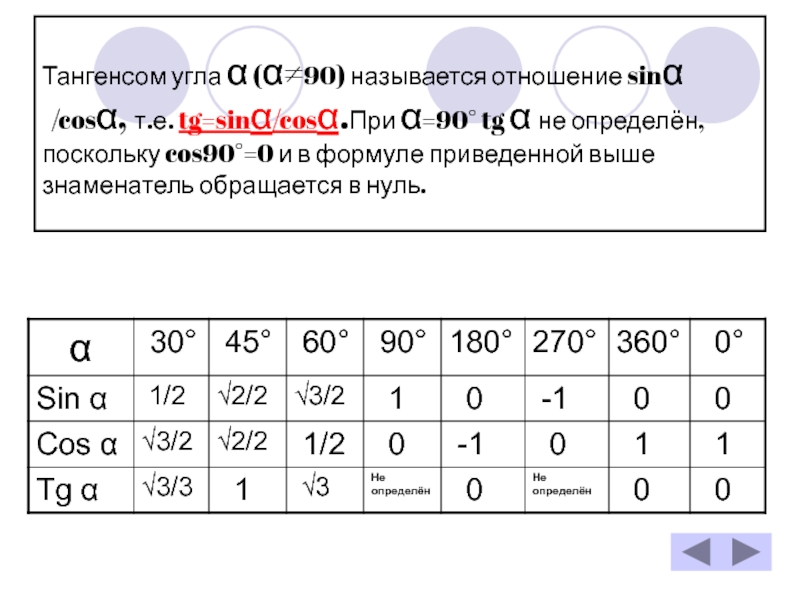
Слайд 8Тангенсом угла α (α≠90) называется отношение sinα /cosα, т.е. tg=sinα/cosα.При
α=90° tg α не определён, поскольку cos90°=0 и в формуле
приведенной выше знаменатель обращается в нуль.Слайд 9
Свойства синуса, косинуса, тангенса и котангенса.
Знаки sin a.
Знаки cos a.
Знаки tg a и ctg a.
Слайд 10Знаки sin a.
Так как sin a=y/R, то знак
sin a зависит от знака y. В 1 и 2
четвертях y>0, а в 3 и 4 четвертях y<0. Значит: sin a>0, если а является углом 1 или 2 четверти, и sin a<0, если а является углом 3 или 4 четверти.90
360
0
270
180
+
-
-
+
Слайд 11Знаки cos a.
Знак cos a зависит от знака
x, так как cos a=x/R. В 1 и 4 четвертях
x>0, а во 2 и 3 четвертях x<0. Поэтому: cos a>0, если а является углом 1 или 4 четверти, и cos a<0, если а является углом 2 или 3 четверти.270
90
-
+
-
+
180
360
0
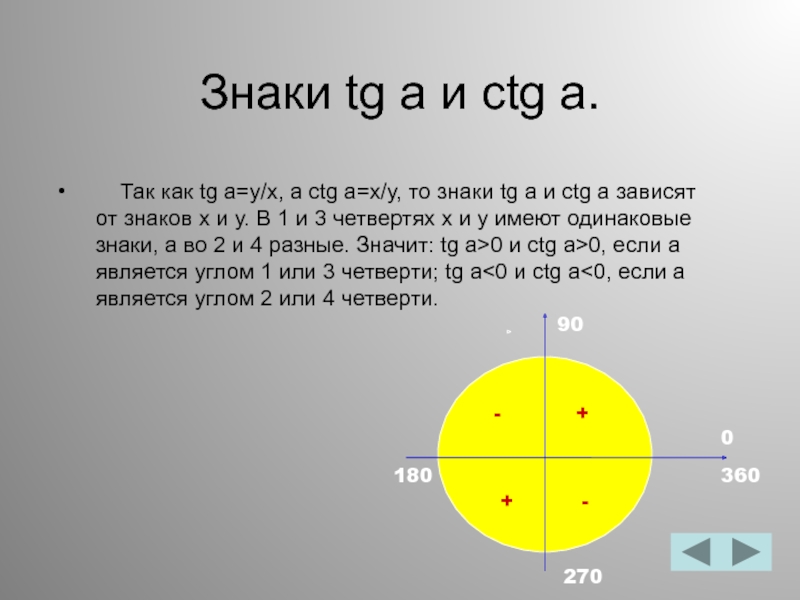
Слайд 12Знаки tg a и ctg a.
Так как tg
a=y/x, а ctg a=x/y, то знаки tg a и ctg
a зависят от знаков x и y. В 1 и 3 четвертях x и y имеют одинаковые знаки, а во 2 и 4 разные. Значит: tg a>0 и ctg a>0, если а является углом 1 или 3 четверти; tg a<0 и ctg a<0, если а является углом 2 или 4 четверти.270
360
0
90
180
-
+
+
-
Слайд 13Формулы для вычисления координат точки
Пусть задана система координат Oxy и
дана точка А(x;y).
Выразим координаты точки А через длину отрезка ОА
и угол a: М- точка пересечения луча ОА с единичной полуокружностью. По формуле x=cosa, y=sina, координаты М(cosa;sina) ОМ{cosa;sina}, ОА{x;y}
По лемме о коллинеарных векторах: ОА=ОА ∙ ОМ,
X=OA ∙ cosa, Y=Oa ∙ sina
M(cosa;sin a)
А(x;y)
a
y
x
O