ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ЭЛЕКТРОТЕХНИКИ лекция № 5

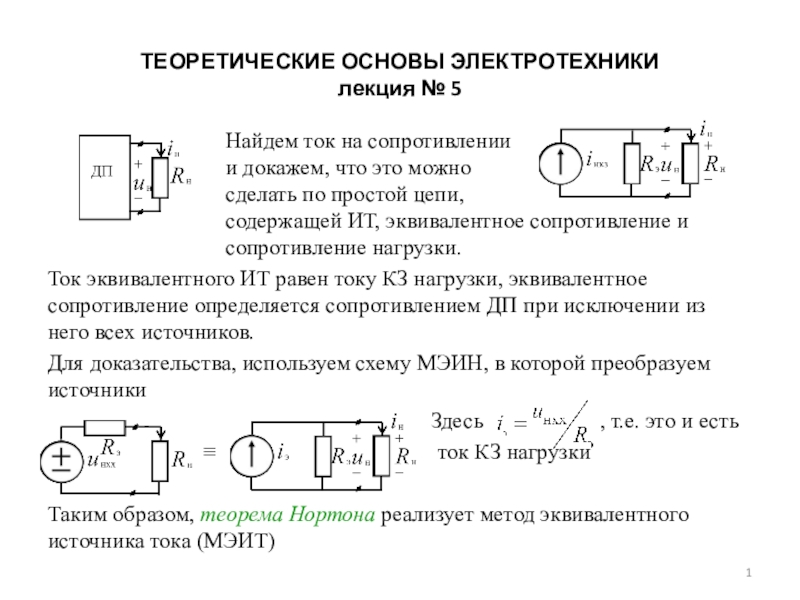
Найдем ток на сопротивлении
и докажем, что это можно
сделать по простой цепи,
содержащей ИТ, эквивалентное сопротивление и
сопротивление нагрузки.
Ток эквивалентного ИТ равен току КЗ нагрузки, эквивалентное сопротивление определяется сопротивлением ДП при исключении из него всех источников.
Для доказательства, используем схему МЭИН, в которой преобразуем источники
Здесь , т.е. это и есть
≡ ток КЗ нагрузки

Таким образом, теорема Нортона реализует метод эквивалентного источника тока (МЭИТ)

узловых напряжений (МУН)
Принимаем напряжение одного из произвольно выбранных узлов схемы

известным и равным 0, этот узел считаем базисным. Предполагаем, что напряжения остальных узлов выше базисного, рассчитываем их относительно базисного узла.
Число независимых уравнений МУН nМУН = nЗТК= nУ -1.
Источники напряжения рекомендуется преобразовать в источники тока (см. 2.2.1).
Напряжение в ветви исходной схемы равно разности узловых напряжений соответствующих узлов ветви.
МУН основывается на ЗТК: в узле сумма токов R-ветвей (выраженная через узловые напряжения и проводимости R-ветвей) уравновешивается суммой токов ИТ.

- узловые

токи, равные алгебраической сумме токов источников в соответствующем узле, при этом вытекающий из узла ток источника принимают отрицательным.

не преобразуемых ИН, тогда базисным узлом над считать общий узел

всех ИН; поскольку при этом напряжение второго узла каждого ИН известно, легко записать упрощенные (вырожденные) уравнения МУН для вторых узлов ИН (с учетом полярности).
Если не все ИН имеют общий узел, следует проделать преобразования

- взаимные сопротивления контуров 1 и
2, 1 и 3, n и m соответственно. Они равны сумме сопротивлений, через которые текут оба контурных тока: с «+», если токи сонаправлены, с «−», если противонаправлены.

Здесь - собственные сопротивления контуров 1, 2, …, n, они равны сумме сопротивлений по обходу контура. Всегда больше нуля.

- контурные напряжения, равные алгебраической сумме напряжений источников по обходу соответствующего контура; правило знаков обратное ЗНК (входим в «+» - пишем «−»).

- контурные токи, т.е. искомые переменные, подлежащие определению.

теорему взаимности (обратимости, пассивности).

Теорема: если единственный в цепи ИН uj,

находящийся в ветви “j”, вызывает в ветви “m” ток im, то будучи перенесенным в ветвь “m” он вызовет в ветви “j” тот же самый ток.

n независимыми контурами контурный ток на основании МКТ

определяется по формуле


главный определитель системы, который симметричен относительно главной диагонали в силу равенства взаимных сопротивлений ; определитель с заменой l-го столбца правой частью системы. алгебраическое дополнение элемента «jl» в .
Ток в ветви , если в цепи имеется только один ИН ,
входящий только в j-й контур

,

МУН можно найти сопротивление передачи

2.4.2. Принцип пассивности (обратимости, взаимности)

Проводимости

и сопротивления передачи с одинаковыми индексами (в прямом и обратном порядке) должны быть равны

,