Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Мысленное моделирование и информационные процессы в инженерной работе. Обзор общих понятий и представлений
Содержание
- 1. Мысленное моделирование и информационные процессы в инженерной работе. Обзор общих понятий и представлений
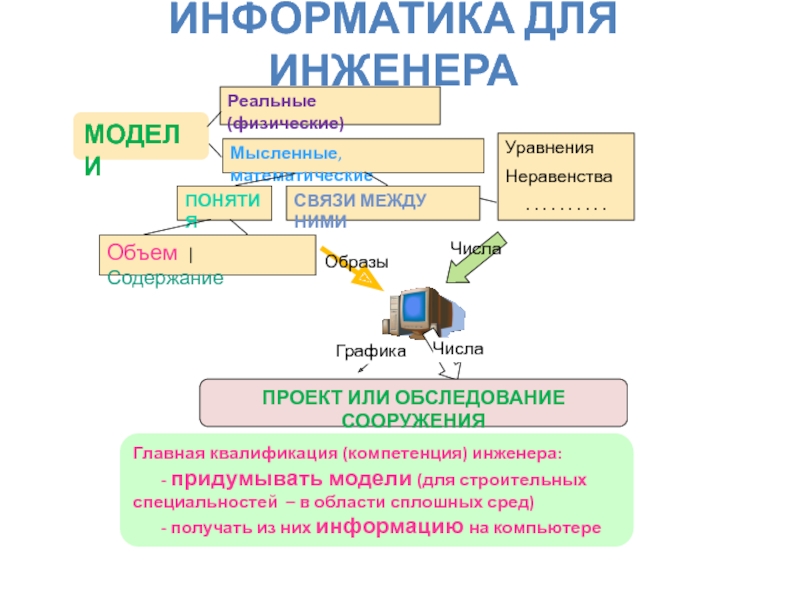
- 2. ИНФОРМАТИКА ДЛЯ ИНЖЕНЕРА
- 3. МОДЕЛИ НЕПРЕРЫВНЫХ ПРОЦЕССОВ И СПЛОШНЫХ СРЕД –
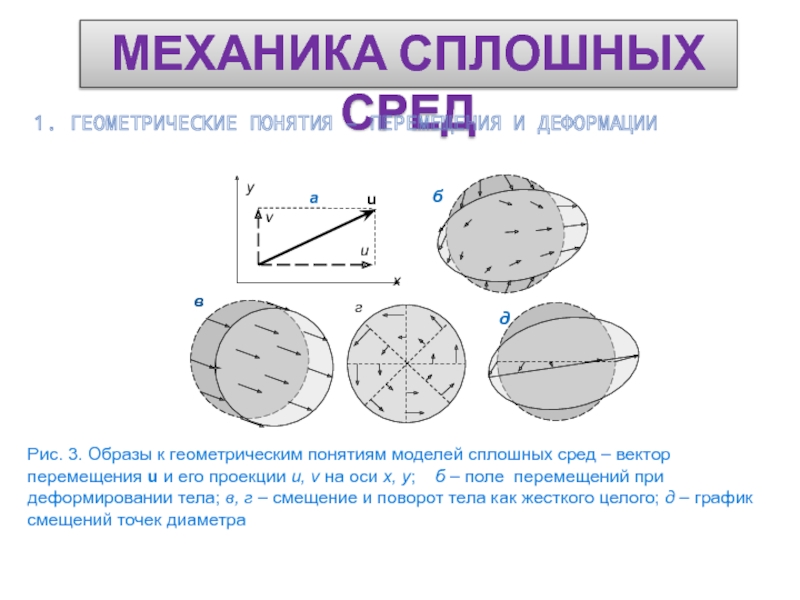
- 4. МЕХАНИКА СПЛОШНЫХ СРЕД1. ГЕОМЕТРИЧЕСКИЕ ПОНЯТИЯ – ПЕРЕМЕЩЕНИЯ И ДЕФОРМАЦИИ
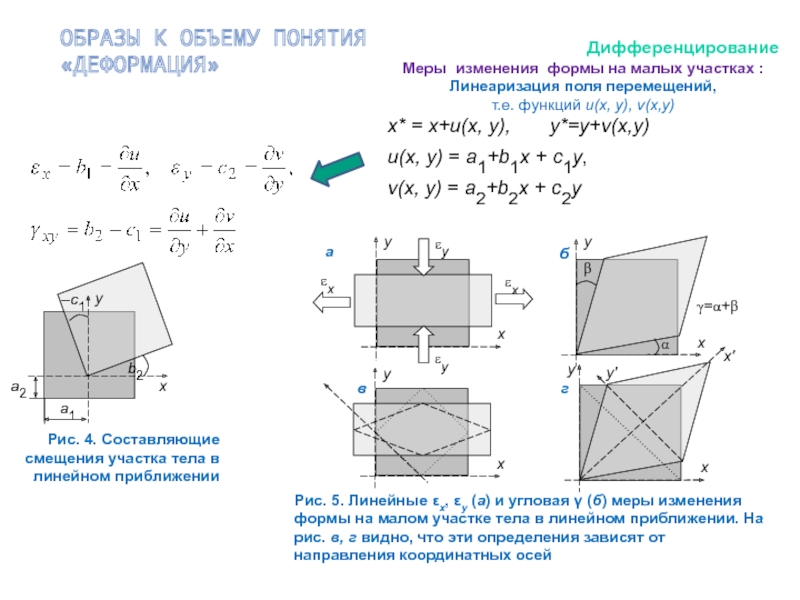
- 5. ОБРАЗЫ К ОБЪЕМУ ПОНЯТИЯ «ДЕФОРМАЦИЯ»
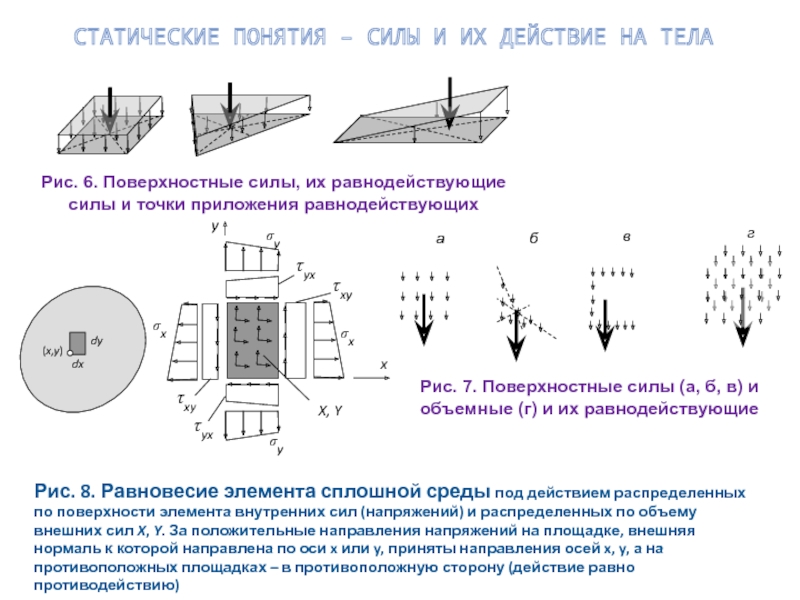
- 6. СТАТИЧЕСКИЕ ПОНЯТИЯ – СИЛЫ И ИХ ДЕЙСТВИЕ НА ТЕЛА
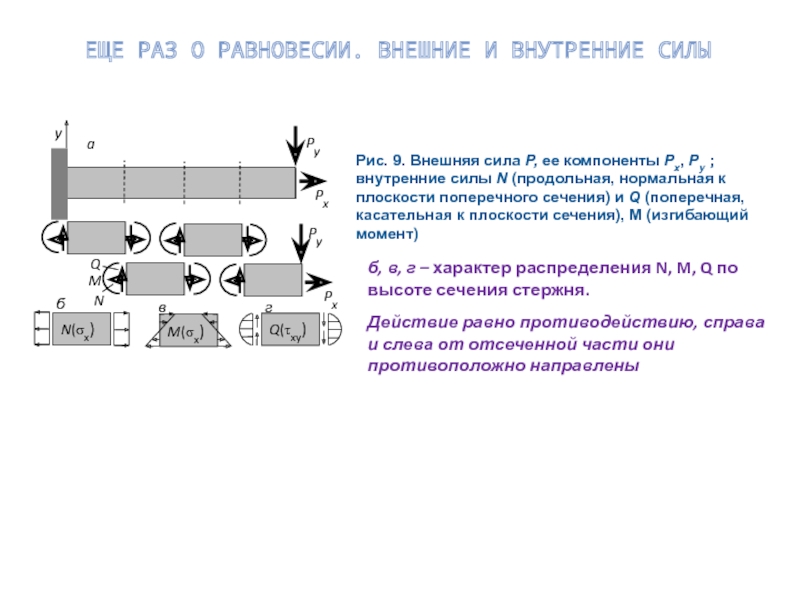
- 7. ЕЩЕ РАЗ О РАВНОВЕСИИ. ВНЕШНИЕ И ВНУТРЕННИЕ СИЛЫ
- 8. Внутренние силы в трехмерном пространствеНо они же
- 9. Физические понятия (упругость, пластичность и др.)
- 10. Все три стороны задачи (и соответствующие группы
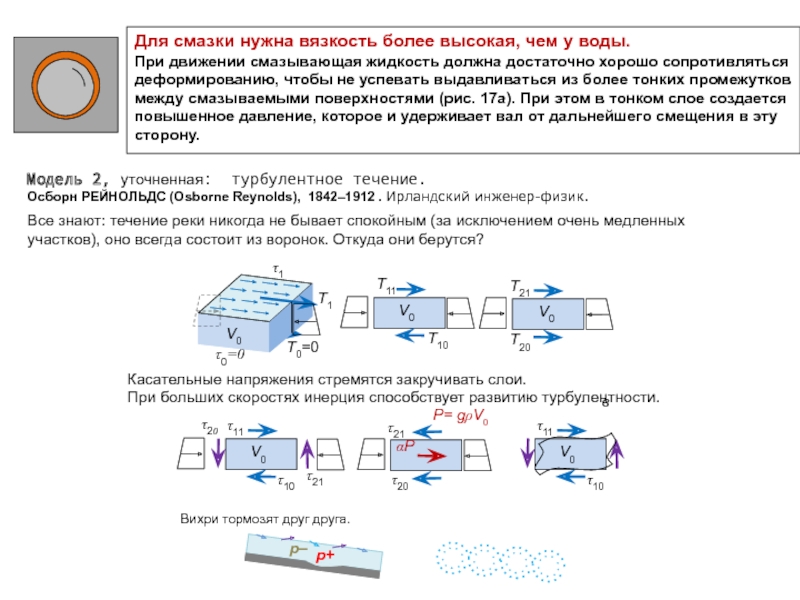
- 11. Особенности моделирования (т.е. механики) жидкостей и газов
- 12. Слайд 12
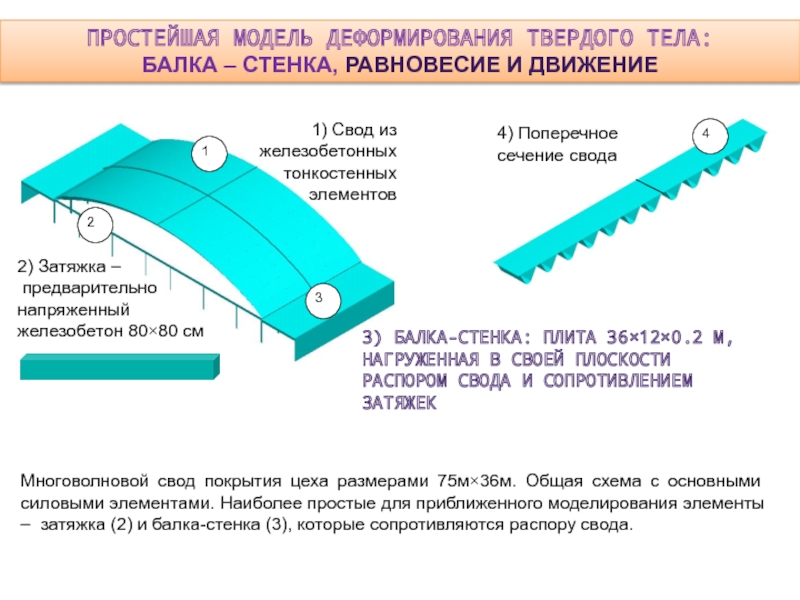
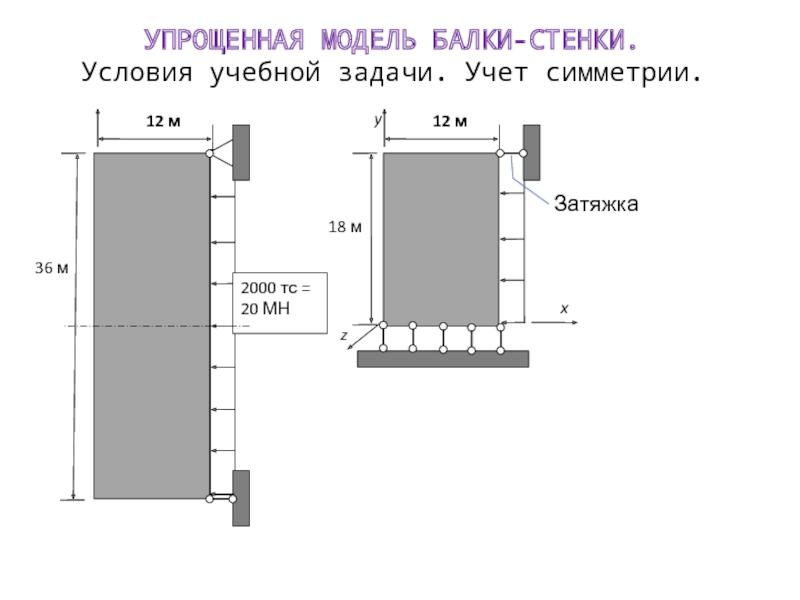
- 13. ПРОСТЕЙШАЯ МОДЕЛЬ ДЕФОРМИРОВАНИЯ ТВЕРДОГО ТЕЛА:БАЛКА – СТЕНКА, РАВНОВЕСИЕ И ДВИЖЕНИЕ
- 14. Слайд 14
- 15. Слайд 15
- 16. Слайд 16
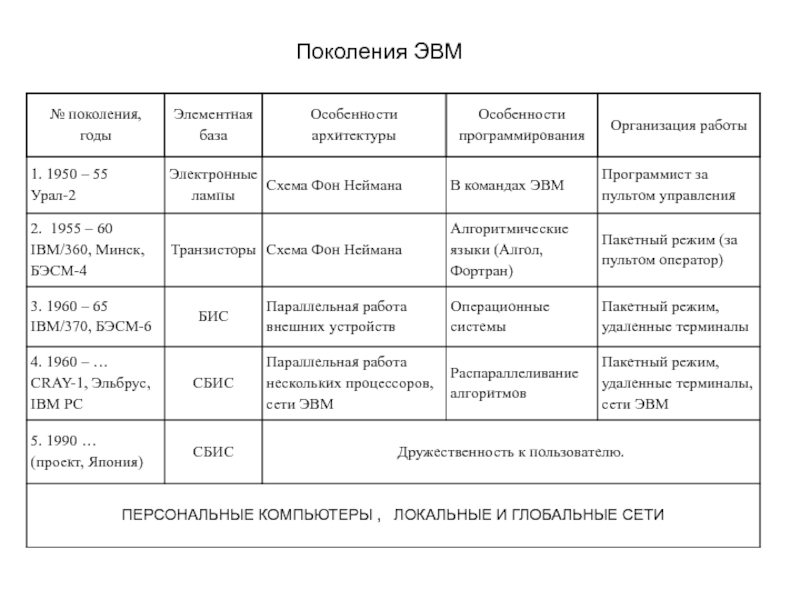
- 17. Поколения ЭВМ
- 18. ЛЕКЦИЯ 2. Мысленное математическое моделирование простейшего непрерывного
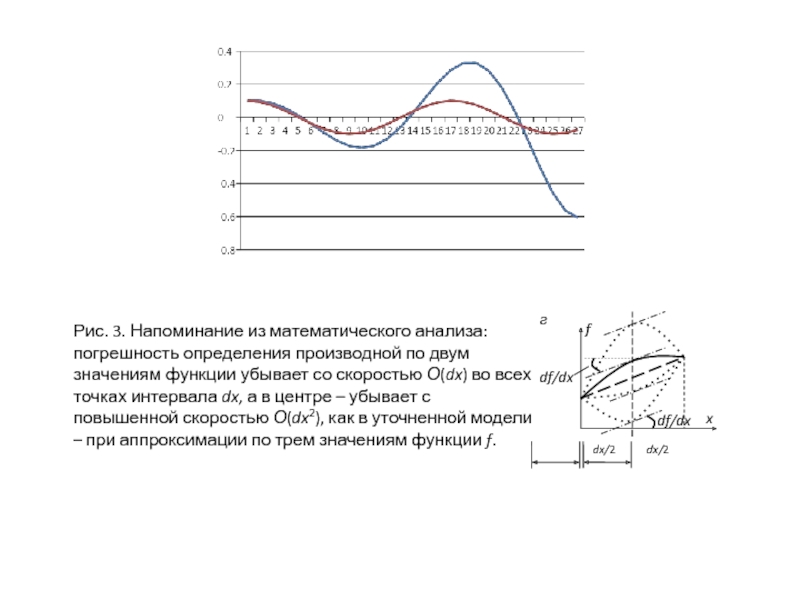
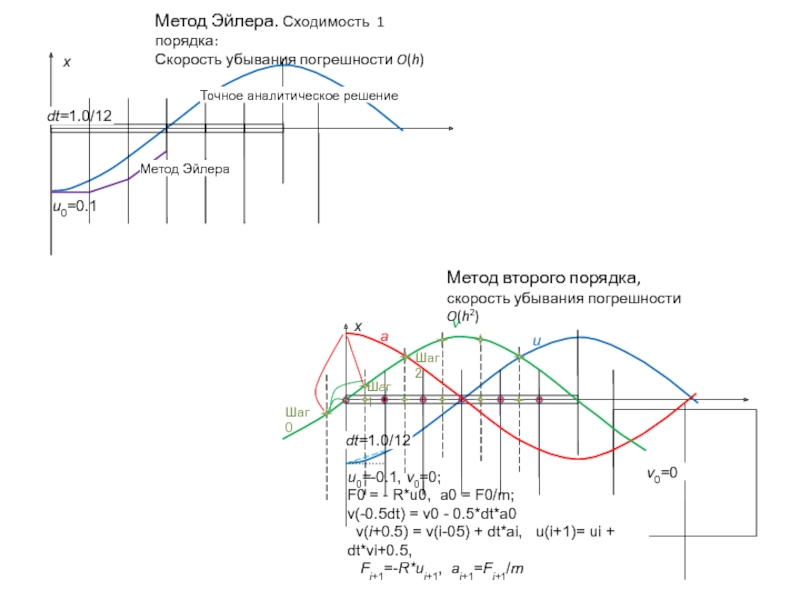
- 19. Дифференцирование процесса движения – разделение на достаточно малые части dtс линейным приближением на каждой части
- 20. Слайд 20
- 21. Слайд 21
- 22. Слайд 22
- 23. Слайд 23
- 24. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1ЛЕКЦИЯ 1. Мысленное моделирование и информационные процессы в инженерной работе.
Обзор общих понятий и представлений
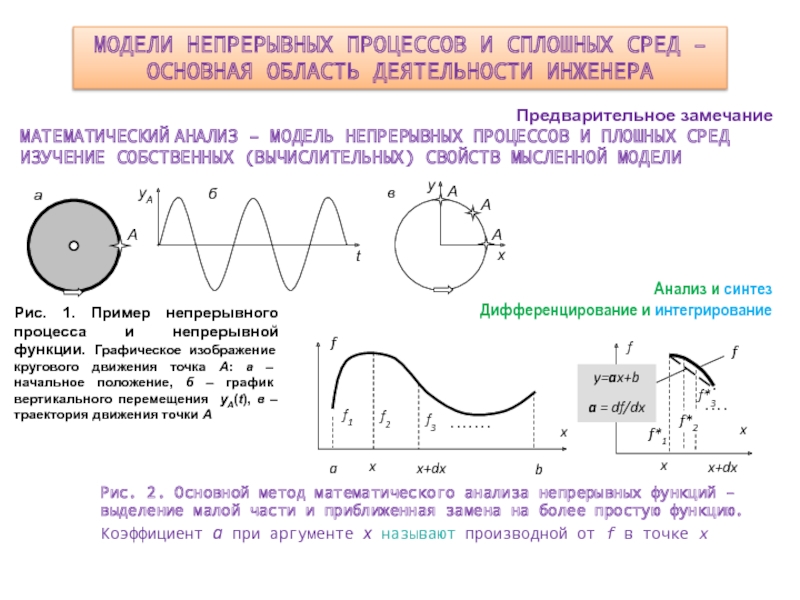
Слайд 3МОДЕЛИ НЕПРЕРЫВНЫХ ПРОЦЕССОВ И СПЛОШНЫХ СРЕД –
ОСНОВНАЯ ОБЛАСТЬ ДЕЯТЕЛЬНОСТИ
ИНЖЕНЕРА
Предварительное замечание
МАТЕМАТИЧЕСКИЙ АНАЛИЗ – МОДЕЛЬ НЕПРЕРЫВНЫХ ПРОЦЕССОВ И ПЛОШНЫХ СРЕД
ИЗУЧЕНИЕ СОБСТВЕННЫХ (ВЫЧИСЛИТЕЛЬНЫХ) СВОЙСТВ МЫСЛЕННОЙ МОДЕЛИ
Анализ и синтез
Дифференцирование и интегрирование
Слайд 8Внутренние силы в трехмерном пространстве
Но они же всегда в трехмерном
пространстве ! ?
В трехмерном пространстве совокупность внутренних сил в одной
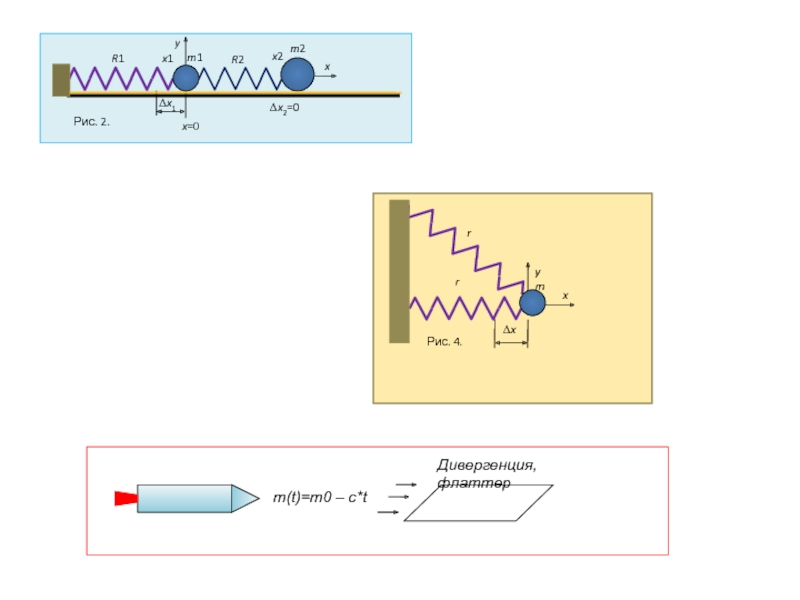
точке изображают параллелепипедом(рис. 1.12): на таком рисунке видно, какие силы относятся к каким площадкам, проходящим через
точку А . Нельзя все девять компонентов трех векторов напряжений показать в одной и той же
точке A, их приходится раздвинуть в центры граней параллелепипеда. Кроме того, на этом же
вырезанном их объема малом параллелепипеде удобно показать положительные направления
внутренних сил (напряжений) на противоположных гранях в соответствии с аксиомой о действии
и противодействии.
Слайд 9Физические понятия (упругость, пластичность и др.)
Для изотропного упругого материала
εx = E(σx–μσy–μσz), εy = E(σy–μσz–μσx),
εz = E(σz–μσx–μσy),где Е - жесткость материала на растяжение и (модуль упругости или модуль Юнга), а коэффициент Пуассона μ (0≤μ≤0.5)показывает, какую долю от εx составляют деформации εy, εz при действии продольной нагрузки σx . Если μ=0, материал не изменяет поперечных размеров при приложении продольной нагрузки. Если μ=0.5, материал несжимаемый, при любых нагрузках не изменяет объема (например, резина).
Другая часть закона связывает угловые деформации с касательными напряжениями (рис. 10, б):
τxy = Gγxy , τyz = Gγyz , τxz = Gγxz ,
здесь G называют сдвиговой жесткостью или модулем сдвига. Для изотропного упругого материала G = E / 2(1+μ).
Слайд 10Все три стороны задачи (и соответствующие группы уравнений) взаимосвязаны.
Обычно
нельзя найти отдельно силы из статических уравнений или перемещения с
деформациями из геометрических уравнений.Обычно нужно совместно решать все три группы уравнений: геометрические, статические и физические.
Слайд 18
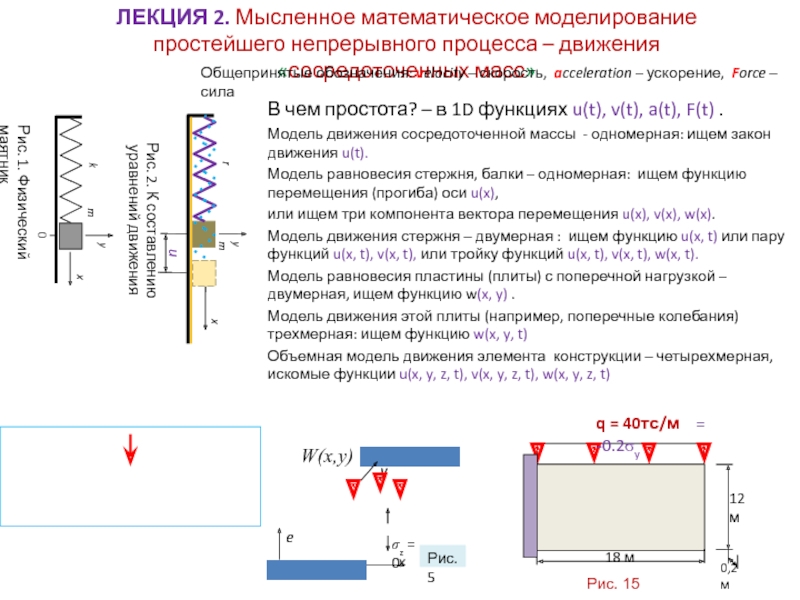
ЛЕКЦИЯ 2. Мысленное математическое моделирование простейшего непрерывного процесса – движения
«сосредоточенных масс»
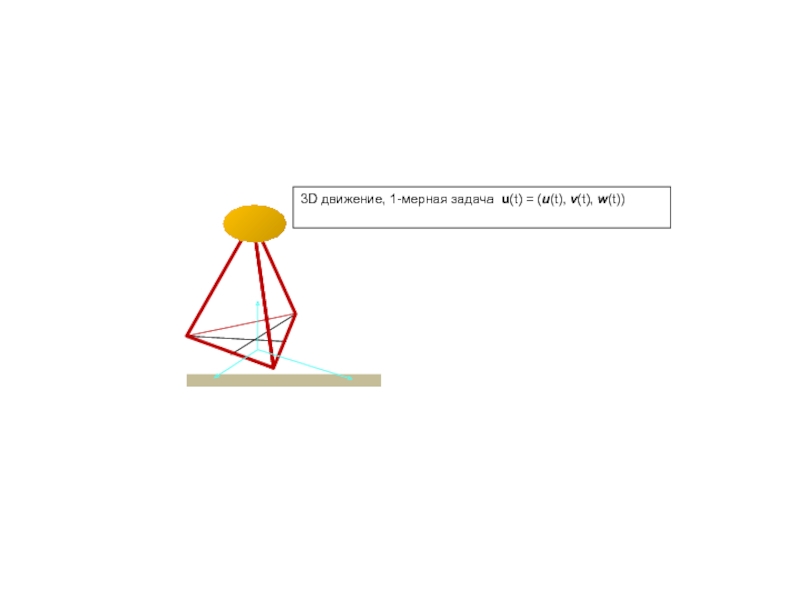
В чем простота? – в 1D функциях u(t), v(t),
a(t), F(t) . Модель движения сосредоточенной массы - одномерная: ищем закон движения u(t).
Модель равновесия стержня, балки – одномерная: ищем функцию перемещения (прогиба) оси u(x),
или ищем три компонента вектора перемещения u(x), v(x), w(x).
Модель движения стержня – двумерная : ищем функцию u(x, t) или пару функций u(x, t), v(x, t), или тройку функций u(x, t), v(x, t), w(x, t).
Модель равновесия пластины (плиты) с поперечной нагрузкой – двумерная, ищем функцию w(x, y) .
Модель движения этой плиты (например, поперечные колебания) трехмерная: ищем функцию w(x, y, t)
Объемная модель движения элемента конструкции – четырехмерная, искомые функции u(x, y, z, t), v(x, y, z, t), w(x, y, z, t)
Общепринятые обозначения: velocity – скорость, acceleration – ускорение, Force – сила