Слайд 1N-мерные векторы
Проф. Сагитов Р.В.
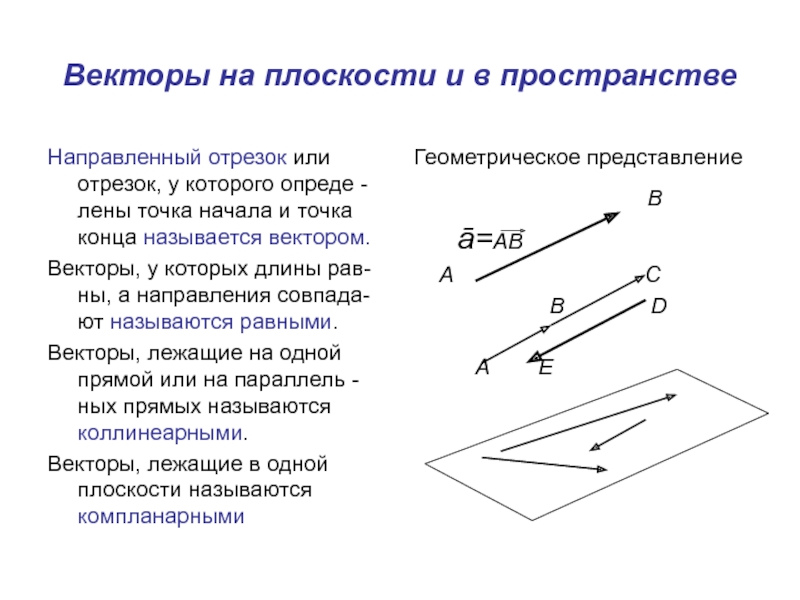
Слайд 2Векторы на плоскости и в пространстве
Направленный отрезок или отрезок, у
которого опреде -лены точка начала и точка конца называется вектором.
Векторы,
у которых длины рав- ны, а направления совпада- ют называются равными.
Векторы, лежащие на одной прямой или на параллель - ных прямых называются коллинеарными.
Векторы, лежащие в одной плоскости называются компланарными
Геометрическое представление
В
ā=АВ
А С
В D
A E
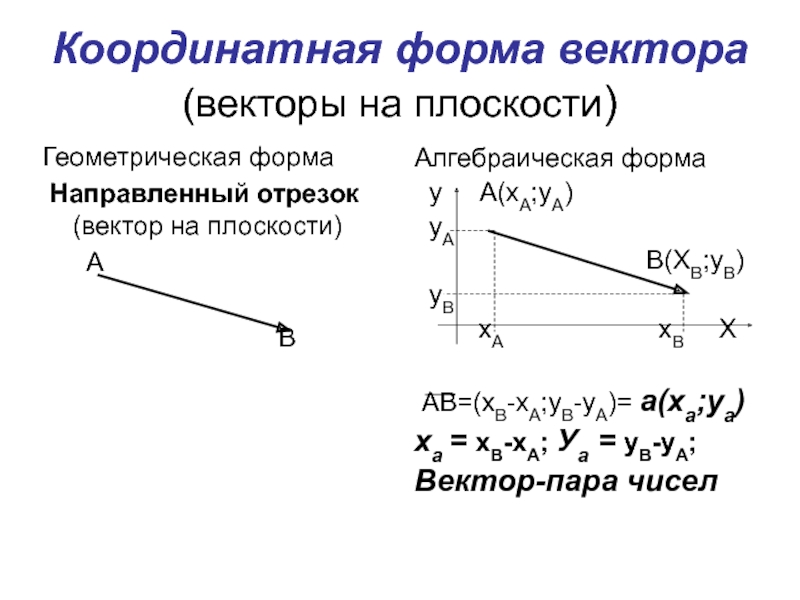
Слайд 3Координатная форма вектора
(векторы на плоскости)
Геометрическая форма
Направленный отрезок (вектор на
плоскости)
А
В
Алгебраическая форма
у А(хА;уА)
уА
В(ХВ;уВ)
уВ
хА хВ Х
АВ=(хВ-хА;уВ-уА)= а(ха;уа)
ха = хВ-хА; Уа = уВ-уА;
Вектор-пара чисел
Слайд 4Координатная форма вектора
(Векторы в пространстве)
Геометрическая форма
Направленный отрезок
(вектор в пространстве)
А
xВ
в х
Алгебраическая форма
z
A(xA;yA;zA)
B(xB;yB;zB)
у хА
AB=(xB-xA;yB-yA;zA-zB) =
=a(xa;ya;za)
Вектор-тройка чисел
Слайд 5Координатная форма N – мерного вектора
N-мерным вектором называется упорядоченный набор
n чисел
А = (а1 ; а2
;… аn); B = (b1 ; b2 ; … bn)
числа аі и bі называются координатами или компонентами векторов А и В количество этих чисел определяет размерность векторов.
A=(1; -2; 5; -4; 3 ); Е1 =(1; 0; 0; 0; 0);
Е3 = (0;0;1;0;0) - единичный вектор
Θ=(0; 0; 0; 0;0) – ноль-вектор
Вектор можно записать в виде столбца А =
Операция замены вектора - строки на вектор – столбец называется транспонированием .(Обозначается А = А׳ или А = Ат).
Очевидно, что (АT)T = А
Слайд 6Действия с векторами
(линейные операции)
Геометрическое представление
1.Сумма векторов
а
а
b b
2. Умножение вектора на число
αA
A A α>0
Алгебраическое представление
1. А + В = (а1 ; а2 ;… аn)+
+ (b1 ; b2 ; … bn)=
=(а1 +b1 ;a2 +b2 ;…an +bn )
2. αА = (αа1;αа2 ;…αаn)
Слайд 7Свойства линейных операций
1.A + B = B + A –
коммутативный
(перестановочный)
2.А + В – С = А + (В - С ) – ассоциативный
(сочетательный)
3. α(А + В) = αА + αВ – дистрибутивный
(распределительный)
4.(α + β)А = .αА + βА - дистрибутивный
Слайд 8Свойства линейных операций
5. Если А + В = Θ, то
А и В противоположные векторы (А = - В)
6. Если
для А≠Θ и В≠Θ А = αВ, то А и В коллинеарные и, если А и В коллинеарные, то найдется такое число α, что А = αВ (α ≠ 0).
Пространства, в которых определены линейные операции, обладающие такими свойствами называются –линейными векторными пространствами
Слайд 9Скалярное произведение векторов
Геометрическое представление
a
φ
b
Длиной вектора или модулем называется расстояние от его начала до его конца, обозначается ׀а׀.
Скалярным произведением называется число равное
аb = ׀a׀·׀b׀·cosφ
Алгебраическое представление
y
ya a α
xa x
a = (xa;ya) b=(хb; уb)
׀a׀=
Cosα= xa/׀a׀ Cosβ=ya/׀a׀
a·b = xa·xb + ya·yb
Слайд 10Скалярное произведение N- мерных векторов
Пусть Х
= ( х1;х2;…хn); У = (y1;y2;… yn) - N
- мерные векторы, тогда скалярным произведением называется число
ХУ = х1у1 +х2у2+…+ хnуn.
Сумма попарных произведений соответствующих координат векторов сомножителей
Слайд 11Свойства скалярного произведения
1.АВ = ВА коммутативный
(перестановочный)
2.kAB = (kA)B = A(kB) ассоциативный (сочетательный) относительно скалярного сомножителя k.
3.(А + В)С = АС + ВС дистрибутивный (распределительный).
4. Если А ≠ Θ и В ≠ Θ, а АВ = 0, то А┴В
( если на плоскости или в пространстве, то перпендикулярны, если в N –мерном пространстве, то ортогональны)
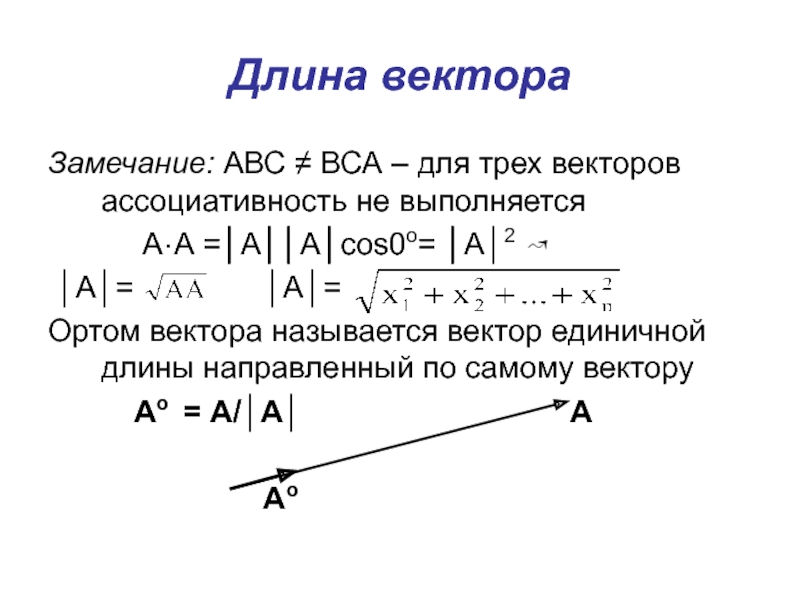
Слайд 12Длина вектора
Замечание: АВС ≠ ВСА – для трех векторов ассоциативность
не выполняется
А·А =│А││А│cos0o= │A│2
↝
│А│= │А│=
Ортом вектора называется вектор единичной длины направленный по самому вектору
Ао = А/│А│ А
Ао
Слайд 13Угол между векторами
Геометрическое представление
А
φ
В
AB
Cos φ =
│A││B│
Алгебраическое представление
A = (а1, а2, …,аn)
B = (b1,, b2, …,bn)
a1b1 +a2b2 +…+ anbn
Cosφ =
√ a12+…an2 √b12+…bn2
Пространство в котором определено скалярное произведение векторов называется метрическим пространством, в нем введена метрика (расстояние между точками)
Слайд 14Экономический смысл скалярного произведения
В экономическом смысле, если интерпретировать вектор P
как вектор цен, а вектор Q как вектор объёмов продуктов,
то скалярное произведение этих векторов означает суммарные затраты на приобретенные продукты.
PQ = ∑piqi – суммарные затраты
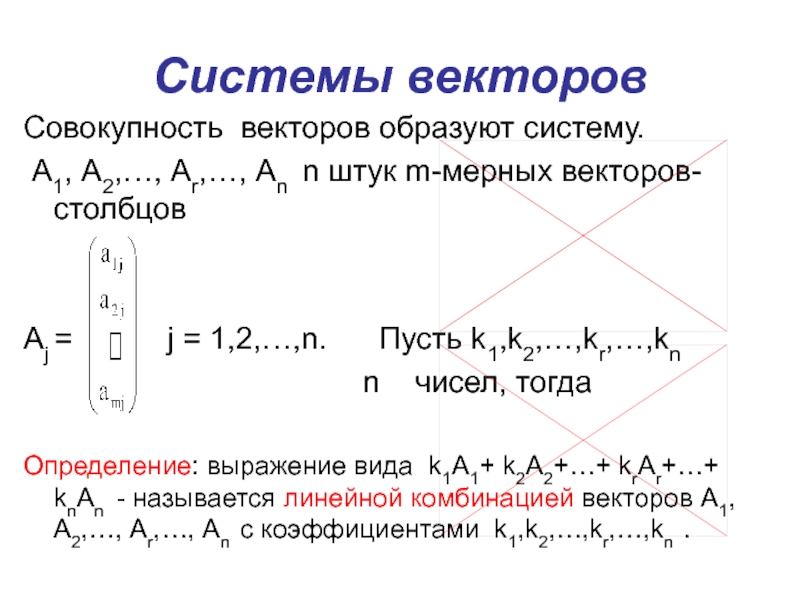
Слайд 15Системы векторов
Совокупность векторов образуют систему.
А1, А2,…, Аr,…, Аn
n штук m-мерных векторов-столбцов
Аj =
j = 1,2,…,n. Пусть k1,k2,…,kr,…,kn
n чисел, тогда
Определение: выражение вида k1А1+ k2А2+…+ krАr+…+ knАn - называется линейной комбинацией векторов А1, А2,…, Аr,…, Аn с коэффициентами k1,k2,…,kr,…,kn .
Слайд 16Примеры линейных комбинаций векторов
Слайд 17Векторная форма записи системы линейных уравнений
Пусть дана система линейных уравнений
Обозначим
столбцы коэффициентов через векторы Аj j=1,2,…,n,а столбец свободных членов
через вектор В
Слайд 18Векторная форма записи системы линейных уравнений
Если векторы Аj умножить соответственно
на переменные хj (j=1,2,…,n), то получится линейная комбинация векторов равная
вектору В
А1 х1 + А2 х2 +…+ Аn хn = В или ∑Аjxj = B
Это векторная форма записи системы линейных уравнений
Слайд 19Системы векторов : линейная зависимость и линейная независимость системы векторов
Рассмотрим
линейную комбинацию
векторов и приравняем ее к ноль-вектору
k1А1+ k2А2+…+ krАr+…+ knАn
= Θ это однородная система линейных уравнений.
Она имеет или только нулевое решение или существует и ненулевое.
Определение: Если система имеет только нулевое решение, то векторы линейно независимые. Если найдется ненулевое решение, то линейно зависимые
Слайд 20Свойства понятий линейная зависимость и линейная независимость системы векторов
1. Если
часть системы векторов линейно зависимая, то и вся система векторов
линейно зависимая.
2. Если система векторов линейно независимая, то любая ее часть векторов тоже линейно независимая.
3. Для того чтобы система векторов была линейно зависимой необходимо и достаточно, чтобы какой – либо вектор раскладывался по остальным векторам.
4.Если число векторов n, входящих в систему больше чем размерность векторов m (n > m), то система векторов линейно зависимая.
Слайд 21Базис системы векторов
Определение: базисом системы векторов называется такая ее часть,
которая линейно независимая и по которой может быть разложен любой
вектор системы.
Слайд 22Свойства базиса системы векторов
Теорема 1. Каждый вектор системы раскладывается по
базису системы единственным образом.
Теорема 2. Если система содержит систему единичных
векторов, то они образуют базис этой системы
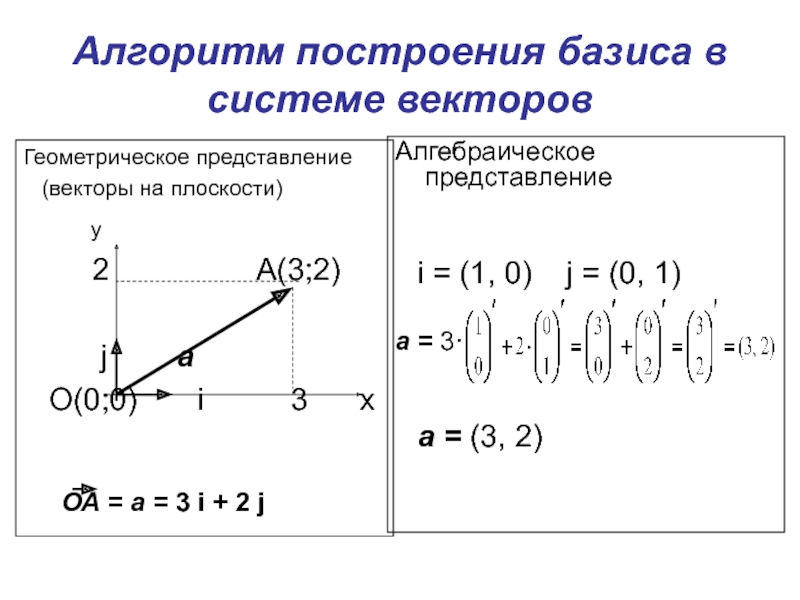
Слайд 23Алгоритм построения базиса в системе векторов
Геометрическое представление
(векторы на
плоскости)
у
2 А(3;2)
j a
О(0;0) i 3 x
Алгебраическое представление
i = (1, 0) j = (0, 1)
a = 3·
a = (3, 2)
ОА = a = 3 i + 2 j
Слайд 24Алгоритм построения базиса в системе векторов
Если система содержит единичные векторы,
то они и образуют базис.
Е1 = (1,0,0,0,0)
А = (3,-2,4,-1,0)
Е2 = (0,1,0,0,0) А = 3Е1- 2Е2+4Е3 –1Е4+0Е5
Е3 = (0,0,1,0,0)
Е4 = (0,0,0,1,0)
Е5 = (0,0,0,0,1)
Слайд 25Алгоритм построения базиса в системе векторов
Определение: две системы векторов А1,А2,…,
Аr ,…, Аn и В1,В2,…, Вr,…,Вn называются равносильными, если равносильны
системы линейных уравнений
А1х1 +А2х2 +…+ Аr хr +…+ Аnхn = Θ
В1х1 + В2х2 +…+ Вrхr +… + Вnхn = Θ
Слайд 26Алгоритм построения базиса в системе векторов
Теорема 3. Пусть системы векторов
А1,А2,…, Аr ,…, Аn и В1,В2,…, Вr,…,Вn равносильные, тогда, если
векторы А1,А2,…, Аr образуют базис в первой системе, то соответствующие им векторы В1,В2,…, Вr образуют базис во второй системе.
Слайд 27Алгоритм построения базиса в системе векторов
Пусть дана система векторов А1;
А2;… Аn
Составим систему однородных линейны уравнений, соответствующую данной системе векторов:
А1х1 + А2х2 +…+ Аnхn = Θ;
Приведем эту систему к равносильной разрешенной системе линейных уравнений Е1х1+ Е2х2+…+Еrхr+ +А΄r+1хr+1+…+ А΄nхn = Θ;
Слайд 28Полученные системы линейных однородных уравнений равносильные, поэтому системы векторов А1;
А2;… Аn и Е1; Е2;…Еr ;… А΄r+1;… А΄n тоже
равносильны. В соответствии с теоремой 3 т.к. векторы Е1; Е2;…Еr образуют базис, то соответствующие векторы А1; А2;… Аr в равносильной системе тоже образуют базис. Вектор Аj будет раскладываться по базису А1; А2;… Аr с коэффициентами, являющимися компонентами вектора А΄j в разрешенной системе.
Пример. Найти базис в системе векторов:
А1 =(1,2,-1,4); A2 =(-1,1,2,-3); A3 =(3,-1,1,-2); A4 =(2;3;4;-4); A5 =(-4;2;1;-1).
Слайд 29Ранг системы векторов
Рангом системы векторов называется число векторов в базисе
системы
Слайд 30Теория систем линейных уравнений
Запишем систему линейных уравнений в векторном виде
А1х1
+ А2х2 +…+Аrхr+…+Аnхn = В
Теорема 4 (Кронекера- Капелли)
Система линейных уравнений
совместна тогда и только тогда, когда ранг системы векторов А1; А2;… Аn равен рангу системы векторов А1; А2;… Аn;В
Слайд 31Альфредо Капелли (1855-1910) итальянский математик
Леопольд Кронекер (1823-1891) немецкий математик
Слайд 32Фундаментальная система решений однородной системы уравнений
Или в векторном виде
А1х1 + А2х2 +…+ Аnхn = Θ;
Слайд 33Свойства решений однородной системы линейных уравнений
1.Если вектор Λ=(λ1; λ2;…;λn) является
ненулевым решением однородной системы, то и вектор к·Λ = (кλ1;кλ2;…;кλn)
тоже ее решение.
2.Если вектора Λ1 и Λ2 являются решениями однородной системы, то и сумма Λ1 + Λ2 также является ее решением.
3.Если Λ1;Λ2;…;Λr являются решением однородной системы, то и любая их линейная комбинация k1Λ1+ k2Λ2+…+ krΛr тоже решение
Слайд 34Фундаментальная система решений однородной системы уравнений
Определение: Фундаментальной системой решений однородной
системы линейных уравнений называется линейно независимая система векторов-решений F1;F2;…;Fk по
которой раскладывается любое решение системы
Х = t1F1 + t2F2+…+ tkFk.
Слайд 35Теорема существования фундаментальной системы решений
Теорема 5: Если ранг r системы
векторов, соответствующих однородной системе уравнений, меньше, чем число переменных n
(r < n), то система имеет фундаментальную систему решений, состоящую из n – r векторов-решений
Слайд 36Пример
Найти фундаментальную систему решений однородной системы
х1 + х2 -5х3 - 7х4 =
0
2х1 +х2 +4х3 + х4 = 0
3х1 +2х2 –х3 - 6х4 = 0
Равносильная разрешенная система имеет вид
х2 - 14х3 -15х4 = 0
х1 + 9х3 + 8х4 =0
А3 = 9А1 – 14 А2 F1 = (-9, 14,1,0)
A4 = 8A1 - 15 A2 F2 = (-8,15,0,1)
Слайд 37Множество решений неоднородной системы линейных уравнений
Теорема 6: Множество решений неоднородной
системы
имеет вид:
Х = К + , где К частное решение
неоднородной системы;
Fi – множество векторов-решений фундаментальной системы решений однородной системы;
−∞< ti <∞
Слайд 38Геометрические приложения
Уравнение линии
у
(x-a)2 + (y-b)2 = r2 – окружн.
y = ax2 +bx + c - парабола
r M(x,y) а>0
b D<0
a x
Определение: уравнение связывающее координаты х и у называется уравнением линии , при соблюдении следующих условий:
Координаты каждой точки, лежащей на линии удовлетворяют уравнению,
Координаты точки не лежащей на линии не удовлетворяют уравнению
Слайд 39Уравнение прямой
Уравнение прямой, проходящей через две точки
у
А(х1у1)
В(х2у2)
х
М(х,у)
Вектор АВ коллинеарен вектору АМ
х-х1 у-у1
х2-х1 у2-у1
Слайд 40Уравнение прямой, проходящей через данную точку перпендикулярно заданному вектору
А(хо;уо)
n = (а;b)- нормальный вектор
M(x,y) вектор АМ ┴ n
АМ·n = 0
а(х – хо) + b(у – уо) = 0 или
ах + by + c = 0 , где c = - (axo + byo)
это общее уравнение прямой.
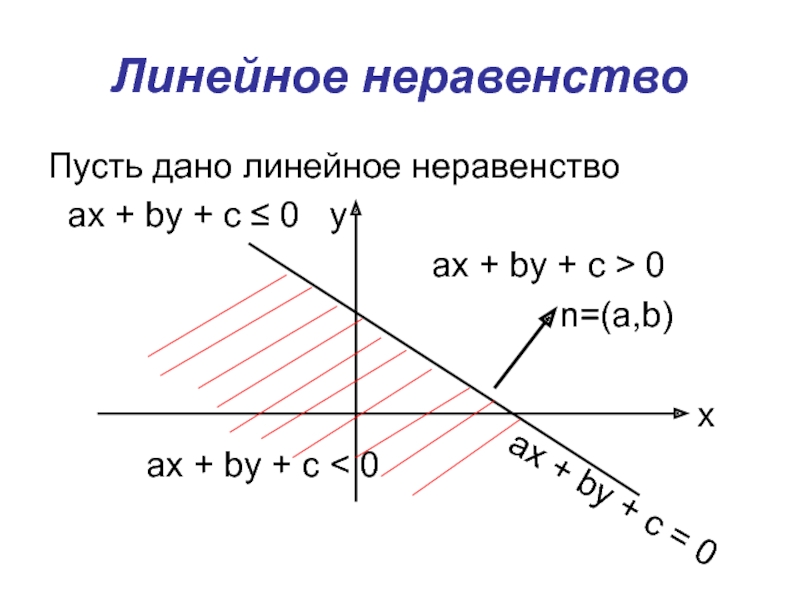
Слайд 41Линейное неравенство
Пусть дано линейное неравенство
ах + by + c
≤ 0 y
ах + by + c > 0
n=(a,b)
x
ах + by + c < 0
ах + by + c = 0
Слайд 42Определения.
Множество точек, координаты которых удовлетворяет неравенству ах + by +
c > 0, образуют верхнюю полуплоскость (πв).
Множество точек, координаты которых
удовлетворяет неравенству ах + by + c < 0, образуют нижнюю полуплоскость (πн).
Множество точек, координаты которых удовлетворяет равенству ах + by + c = 0, образуют прямую линию (πо)
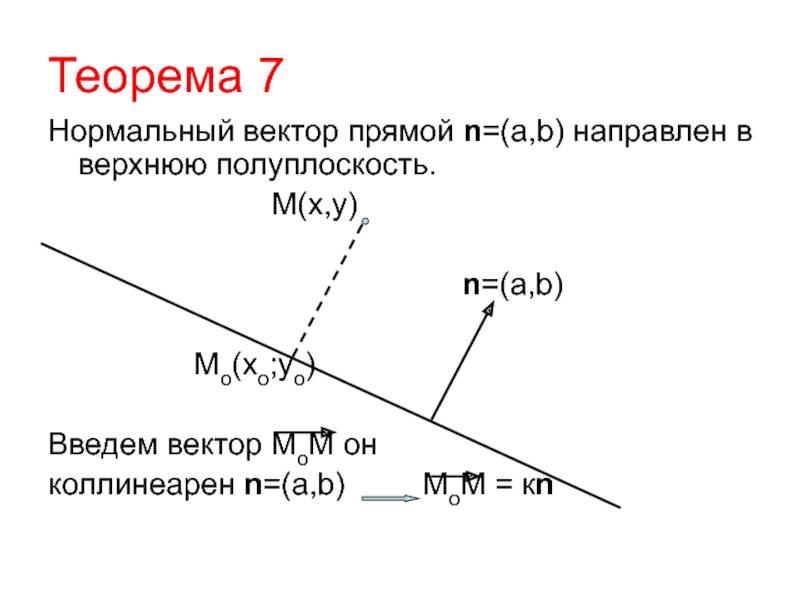
Слайд 43Теорема 7
Нормальный вектор прямой n=(а,b) направлен в верхнюю полуплоскость.
М(х,у)
n=(а,b)
Mо(xo;yo)
Введем вектор МоМ он
коллинеарен n=(а,b) МоМ = кn
Слайд 44Уравнение поверхности
Определение: уравнение связывающее координаты х,у и z называется уравнением
поверхности , при соблюдении следующих условий:
Координаты каждой точки, лежащей на
линии удовлетворяют уравнению,
Координаты точки не лежащей на линии не удовлетворяют уравнению
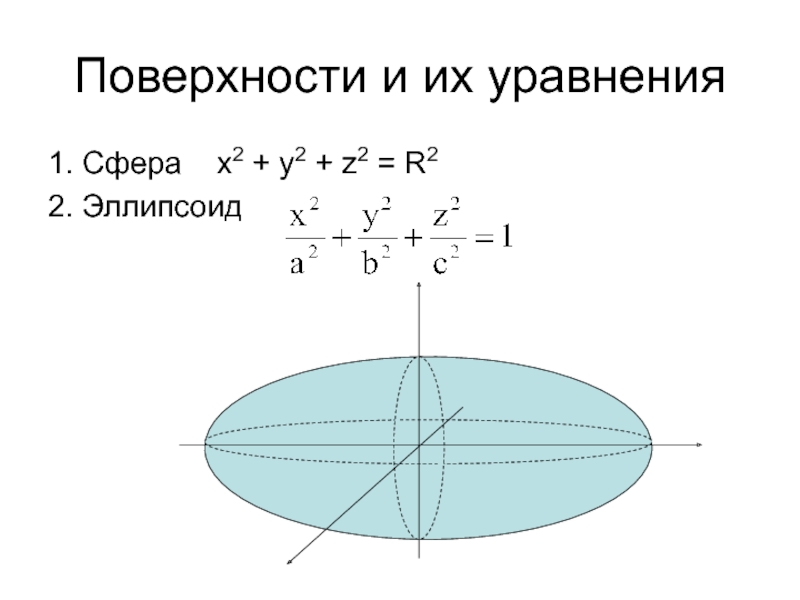
Слайд 45Поверхности и их уравнения
1. Сфера х2 + у2 +
z2 = R2
2. Эллипсоид
Слайд 46Поверхности и их уравнения
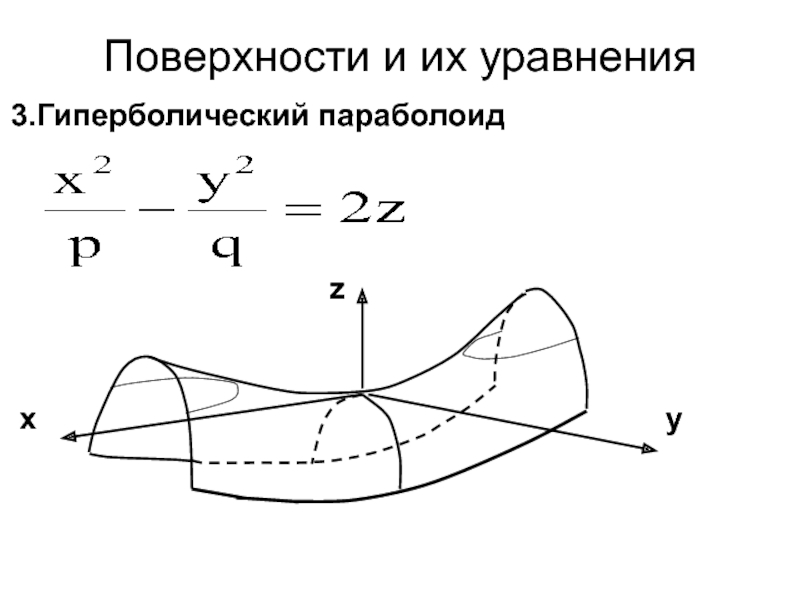
3.Гиперболический параболоид
z
x y
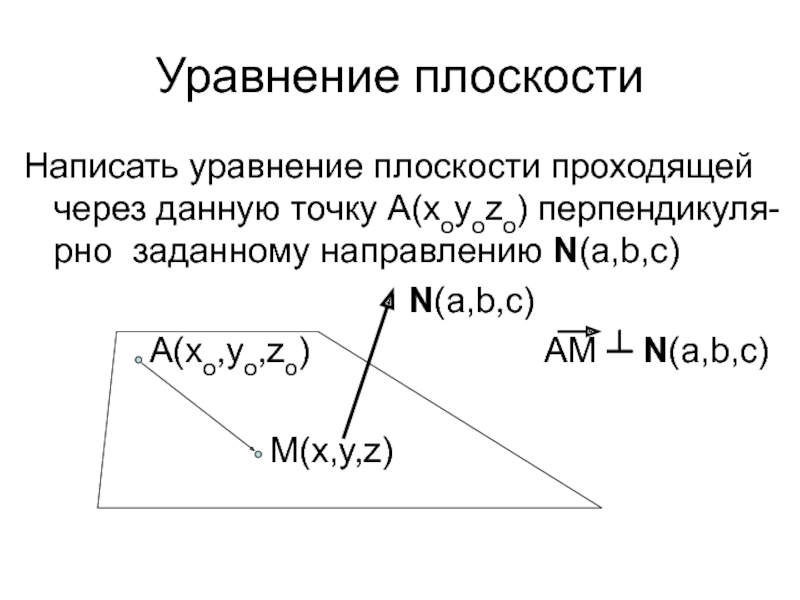
Слайд 47Уравнение плоскости
Написать уравнение плоскости проходящей через данную точку А(хoуozo) перпендикуля-рно
заданному направлению N(a,b,c)
N(a,b,c)
A(xo,yo,zo) AM ┴ N(a,b,c)
M(x,y,z)
Слайд 48Уравнение плоскости
AM ┴ N(a,b,c)
АМ=(х-хo;у-уo;z-zo )
а(х – хo ) + b(y –
yo ) + c(z – zo ) = 0
ax + by + cz + d = 0
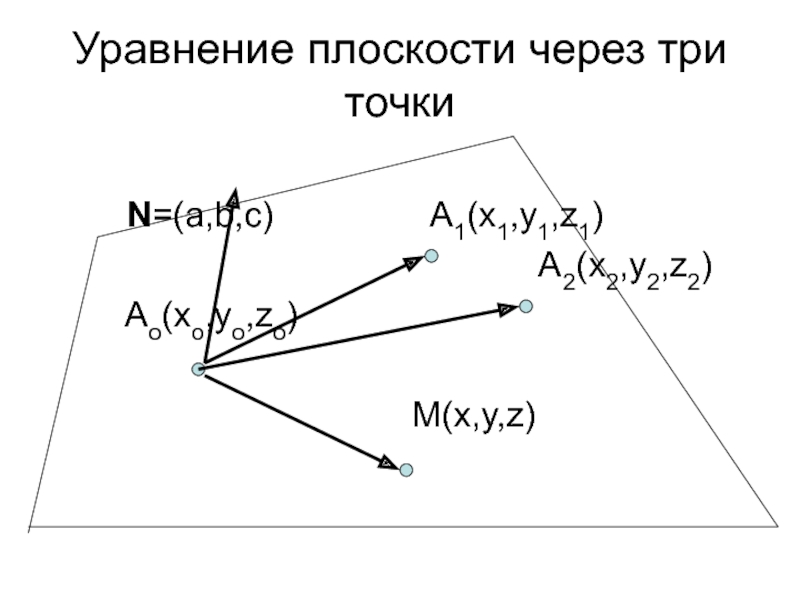
Слайд 49Уравнение плоскости через три точки
N=(a,b,c)
A1(x1,y1,z1)
A2(x2,y2,z2)
Ao(xo,yo,zo)
M(x,y,z)