Слайд 1Концепція вартості грошей в часі
Основний принцип: Гроші зараз коштують більше,
ніж гроші, які будуть отримані в майбутньому (наприклад, через рік),
так як вони можуть бути інвестовані і це принесе додатковий прибуток
Сутність концепції: вартість грошей з часом змінюється з врахуванням норми прибутку на грошовому ринку та ринку цінних паперів. В якості норми прибутку виступає норма кредитного процента або норма виплати дивідендів по простих чи привілейованих акціях.
Слайд 2Вартість грошей в часі: майбутня і теперішня вартість грошей.
Майбутня
вартість грошей - сума інвестованих в теперішній час грошових коштів,
в яку вони перетворяться через визначений період з урахуванням визначної процентної ставки. Визначення майбутньої вартості грошей пов'язано з процесом нарощування цієї вартості.
Теперішня (сучасна) вартість грошей – сума майбутніх грошових надходжень, приведених з врахуванням визначеної процентної ставки до теперішнього моменту часу. Визначення теперішньої вартості грошей пов'язано з процесом дисконтування.
Слайд 3Вартість грошей в часі: основні розрахункові співвідношення
Складним процентом називається
сума доходу, яка створюється в результаті інвестування грошей при умові,
що сума нарахування простого процента не сплачується в кінці кожного періоду, а приєднується до суми основного вкладу і в наступному періоді сама приносить дохід. Основна формула теорії процентів визначає майбутню вартість грошей:
(1)
где PV – теперішнє значення вкладеної суми грошей
FV – майбутнє значення вартості грошей,
n – кількість періодів часу, на яке здійснюються вкладення,
r – норма доходності (прибутковості) від вкладення.
Слайд 4Вартість грошей в часі: основні розрахункові співвідношення
Теперішнє (сучасне) значення визначеної
майбутньої суми грошей визначається за допомогою формули: (2)
Яка є простим
перетворенням попередньої формули:
Слайд 5Вартість грошей в часі: основні розрахункові співвідношення
Приклад 1. Нехай інвестор хоче
отримати $201,14 через 5 роки. Яку суму він повинен покласти
на строковий депозит зараз, якщо депозитна процентна ставка складає 15%?
За допомогою формули (2) легко визначити:
Розглянутий випадок можна пояснити наступним чином:
$100 і $201,14 – це два способи представити одну і ту ж суму грошей в різні моменти часу – $201,14; через пять років рівносильні $100 зараз.
Слайд 6Номінальна сума грошових коштів – це оцінка цієї суми без
врахування зміни купівельної спроможності грошей (гроші на руки).
Реальна сума
грошових коштів – це оцінка цієї суми з врахуванням зміни купівельної спроможності грошей у зв'язку з процесом інфляції.
Напрямки використання:
при корегуванні нарощеної вартості грошових коштів.
при формуванні ставки процента (використовується для нарощування та дисконтування).
при прогнозуванні рівня доходів від інвестицій, враховуючих рівні інфляції.
Вартість грошей в часі:
вплив інфляції
Слайд 7Вартість грошей в часі: вплив інфляції
В процесі оцінки використовуються два
основні показника:
темп інфляції Т, характеризує приріст середнього рівня цін
у визначеному періоді, виражений десятковим дробом. індекс інфляції I (зміна індексу споживчих цін), який дорівнює 1+Т.
Слайд 8Корегування нарощеної вартості з урахуванням інфляції
(3)
где FVnp - реальна майбутня
вартість грошей,
FVn – номінальна майбутня вартість
грошей з врахуванням інфляції.
Якшо r – номінальна ставка процента, яка враховує інфляцію, то розрахунок реальної суми грошей здійснюється за формулою:
(4)
Тобто номінальна сума грошових коштів знижується в (1+Т)n рази у відповідності до зниження купівельної спроможності грошей.
Вартість грошей в часі: вплив інфляції
Слайд 9Вартість грошей в часі: вплив інфляції
Приклад: Нехай номінальна ставка
процента з урахуванням інфляції складає 50%, а очікуваний темп інфляції
в рік 40%. Необхідно визначити реальну майбутню вартість обсягу інвестицій 200 000 умовних грошових одиниць.
Якщо в процесі реального розвитку економіки темп інфляції становить 55%, то
Таким чином , інфляція «з'їдає» прибутковість в процесі інвестування і стає збитковим.
Слайд 10Варість грошей в часі:
вплив інфляції
Можливі три варіанти:
1) r =
T : нарощування реальної вартості грошових коштів не відбувається, так
як приріст їх майбутньої вартості ПОКРИВАЄТЬСЯ інфляцією,
2) r > T : реальна майбутня вартість грошових коштів ЗРОСТАЄ, не дивлячись на інфляцію,
3) r < T : реальна майбутня вартість грошових коштів знижується, тобто процес інвестування стає збитковим.
Слайд 11Загальне співвідношення
1. Інвестор вкладаючи PV під rр процентів річних, очікує
отримати через рік:
2. Якщо темп інфляції становить T процентів
в рік, то майбутнє
значення корегується
3. Таким чином, номінальна процентна ставка дохідності
складає:
Вартість грошей в часі:
вплив інфляції
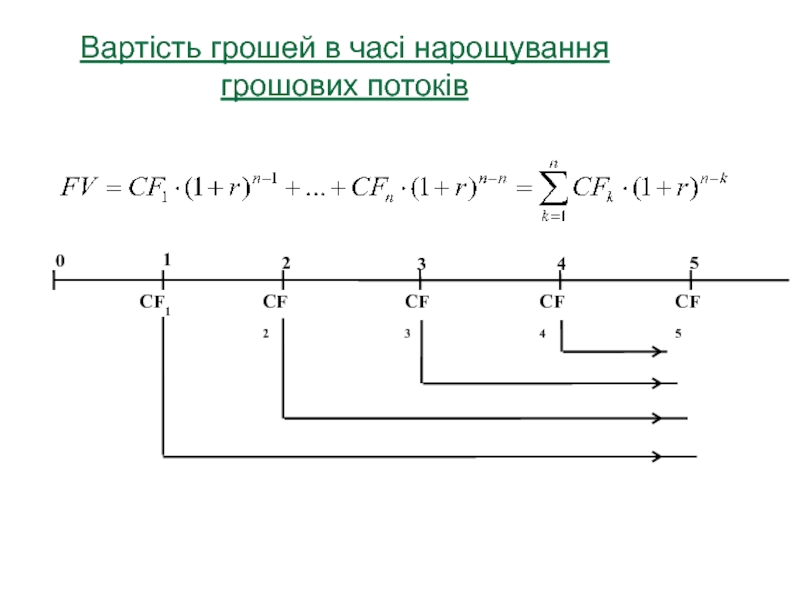
Слайд 12Вартість грошей в часі : нарощування і дисконтування грошових потоків
Грошовий
потік прийнято зображувати на часовій лінії одним із двох способів:
Слайд 13Вартість грошей в часі нарощування грошових потоків
Слайд 14Вартість грошей в часі: нарощування грошових потоків
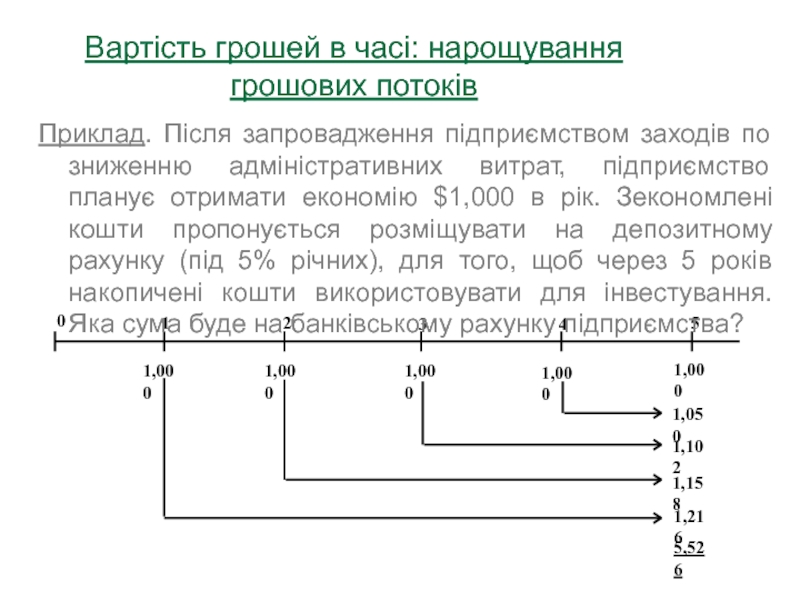
Приклад. Після запровадження підприємством
заходів по зниженню адміністративних витрат, підприємство планує отримати економію $1,000
в рік. Зекономлені кошти пропонується розміщувати на депозитному рахунку (під 5% річних), для того, щоб через 5 років накопичені кошти використовувати для інвестування. Яка сума буде на банківському рахунку підприємства?
Слайд 15
Вартість грошей в часі: нарощування грошових потоків
В даному випадку грошовий
потік складається із однакових щорічних грошових сум. Такий потік називається
ануїтет. Для обрахунку майбутнього значення ануїтету використовується формула (5)
Розрахунок майбутнього значення одинарної суми і ануїтету може здійснюватися за допомогою спеціальних фінансових таблиць.
Слайд 16
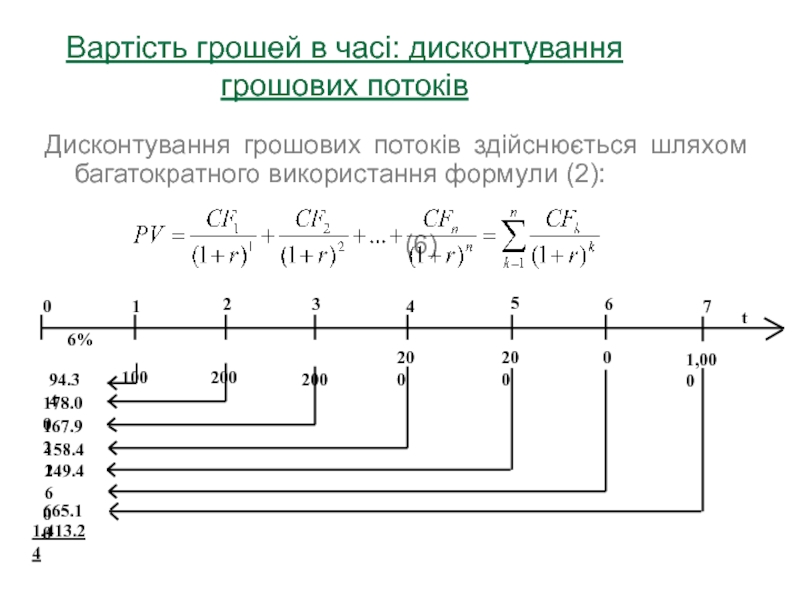
Вартість грошей в часі: дисконтування грошових потоків
Дисконтування грошових потоків здійснюється
шляхом багатократного використання формули (2):
(6)
Слайд 17Вартість грошей в часі: дисконтування грошових потоків
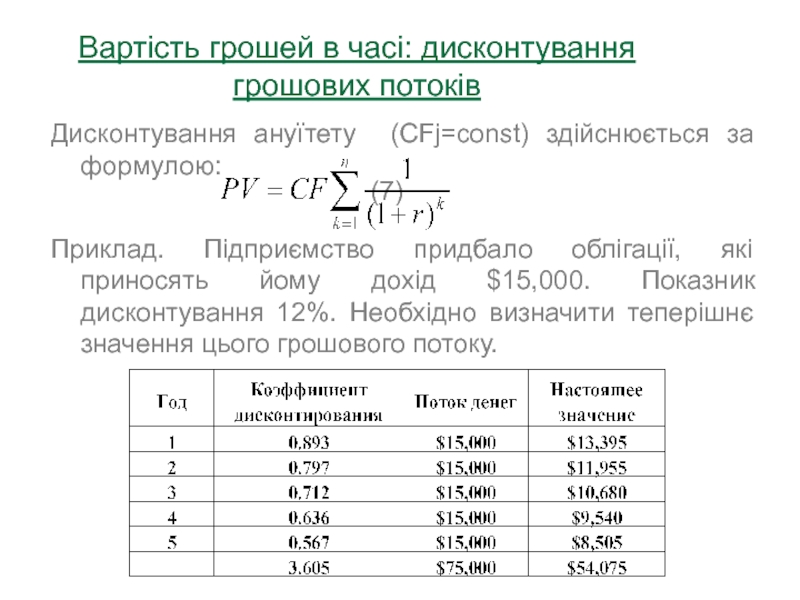
Дисконтування ануїтету (CFj=const) здійснюється
за формулою:
(7)
Приклад. Підприємство придбало облігації, які приносять йому дохід $15,000.
Показник дисконтування 12%. Необхідно визначити теперішнє значення цього грошового потоку.
Слайд 18
Вартість грошей в часі: аналіз альтернативних вкладень
Техніка оцінки вартості грошей
в часі дозволяє вирішити ряд важливих завдань порівняльного аналізу альтернативних
можливостей вкладання грошей.
Приклад. Розглянемо потік $1,000, який генерується якою-небудь інвестицією в реальні активи протягом 3 років. Розрахункова ставка дисконту складає 10%.
Намагаємося послідовно відповісти на ряд питань, пов'язаних з різними ситуаціями походження цього потоку і його використання.
Слайд 19
Вартість грошей в часі: аналіз альтернативних вкладень
Питання 1. Яка сучасна
вартість цього потоку?
Питання 2. Яка майбутня вартість $2,486.85 на
кінець 3 року? (тобто, якби ми вклали гроші у фінансові активи під 10% річних)?
Слайд 20
Вартість грошей в часі: аналіз альтернативних вкладень
Питання 3. Яка майбутня
вартість потоку грошових коштів на кінець 3-го року?
Результати відповідей на
питання 2 і 3 – одинакові.
Висновок: Якщо ми інвестуємо зараз $2,486.85 в реальні активи, и ця інвестиція генерує заданий потік грошей $1,000, $1,000, $1,000, то на кінець 3-го року ми отримуємо ту ж суму грошей $3,310, так якби ми вклали $2,486.85 під 10% річних у фінансові активи.
Слайд 21
Вартість грошей в часі: аналіз альтернативних вкладень
Нехай тепер величина інвестицій
складає $2,200, а генерований потік такий же, що приводить до
кінця 3-го року до $3,310.
Інвестування в фінансові інструменти $2,200 під 10% дає
Отже нам більш вигідно інвестувати кошти в реальні активи.
Слайд 22
Вартість грошей в часі: аналіз альтернативних вкладень
Питання 4. Як зміниться
ситуація, якщо показник дисконту r буде більше, наприклад 12%?
Ми інвестуємо
$2,486.85 в реальні активи, і це призводить до потоку грошових коштів $1,000 кожен рік протягом 3-х років.
тобто PV зменшилося.
Порівняємо FV для $2,486.85 і FV для потоку
Слайд 23Вартість грошей в часі: аналіз альтернативних вкладень
Таким чином ми отримали
a)
інвестування $2,486.85 під 12% річних в фінансові активи призведе до
$3,493.85 через 3 роки
б) інвестиція $2,486.85 в реальні активи, яка генерує грошовий потік $1,000 кожен рік протягом 3-х років, призведе до $3,374.40 до кінця 3-го року.
Висновок: при показники дисконту 12% інвестувати у виробництво не вигідно. Цей висновок із аналізу чистої теперішньої вартості.
Теперішнє значення потоку $2,401.83
Величина інвестицій $2,486.85
Чисте теперішнє значення ($85)
Порівняємо різницю:
$85(1+0.12)3=$119.45 – майбутнє значення різниці
$3,493.85 - $3,374.40 = $119.45. – різниця між а) і б).