Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Написать программу, определяющую пару функций, имеющих на заданном интервале наибольшее число точек пересечения
Содержание
- 1. Написать программу, определяющую пару функций, имеющих на заданном интервале наибольшее число точек пересечения
- 2. Содержание:1. Цель2. Задачи3. Ход работы4. Результаты5. ВыводыКрылов 4282
- 3. Цель:Написать программу, определяющую пару функций, имеющих на заданном интервале наибольшее число точек пересечения.Крылов 4282
- 4. Для достижения этой цели были поставлены задачи:
- 5. Данные:y1=cos(x)y2=sin(x)y3=sqrt(x)-3Промежуток [3;8]Крылов 4282
- 6. Шаг 1.Возьмём три функции как попарная разность исходных:y4=y1-y2y5=y1-y3y6=y2-y3Крылов 4282
- 7. Шаг 2.Разобьём интервал на равные отрезки длинной
- 8. В нашем случае отрезком будет служить разбиение dТо есть:Если Y(Xo)*Y(Xo+d)
- 9. Шаг 3.В цикле рассматриваем каждый участок нашего разбиения и ищем точки пересечения функций:while x
- 10. Шаг 4.Ищем наибольшее из чисел с сс
- 11. Шаг 5.Построение графиков: x=b:0.001:a;gf=sin(x); gff=cos(x);
- 12. Результат работы программы:sin(x) and cos(x)sin(x) and sqrt(x)-3;Крылов 4282
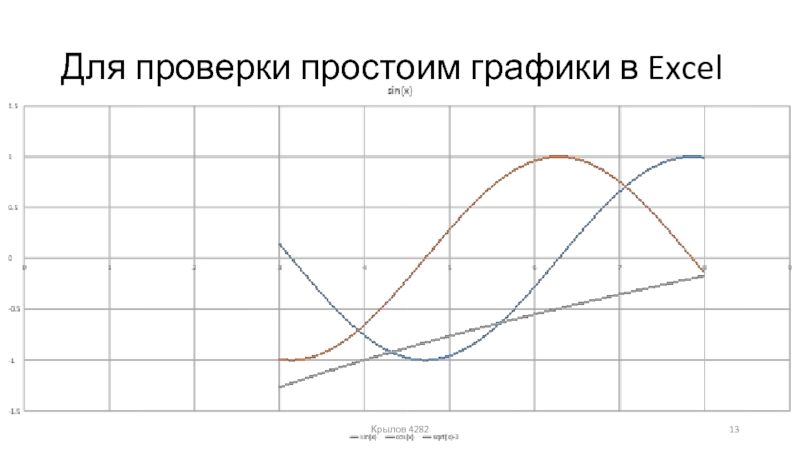
- 13. Для проверки простоим графики в ExcelКрылов 4282
- 14. Вывод:Была изучена среда программирования Matlab, реализован алгоритм
- 15. Скачать презентанцию
Содержание:1. Цель2. Задачи3. Ход работы4. Результаты5. ВыводыКрылов 4282
Слайды и текст этой презентации
Слайд 1Курсовая работа по Информационным технологиям
Выполнил: Крылов Дмитрий Андреевич
Преподаватель: Фирсов Дмитрий
Дмитриевич
Слайд 3Цель:
Написать программу, определяющую пару функций, имеющих на заданном интервале наибольшее
число точек пересечения.
Крылов 4282
Слайд 4Для достижения этой цели были поставлены задачи:
Изучить среду программирования Matlab
Найти
удобный способ определения точек пересечения функций
Реализовать выполнения найденного алгоритма в
п.2. в среде MatlabПостроить графики функций
Крылов 4282
![Данные:y1=cos(x)y2=sin(x)y3=sqrt(x)-3Промежуток [3;8]Крылов 4282](/img/thumbs/72ed5c20c618bb920c5facd4e76b5851-800x.jpg "Написать программу, определяющую пару функций, имеющих на заданном интервале наибольшее число точек пересечения Данные:y1=cos(x)y2=sin(x)y3=sqrt(x)-3Промежуток [3;8]Крылов 4282")
Слайд 7Шаг 2.
Разобьём интервал на равные отрезки длинной d
Теорема: Если произведение
значений функции на концах отрезка меньше нуля, то существует точка,
принадлежащая отрезку, где функция обращается в нуль.y
x
Крылов 4282
Слайд 8
В нашем случае отрезком будет служить разбиение d
То есть:
Если Y(Xo)*Y(Xo+d)
то в интервале [Xo;Xo+d] лежит точка пересечения Y с осью
абсцисс( Y=0)Так как наши функции представляют собой разность функций то
(например)
y6=y3-y2=0 отсюда следует, что y3(a)=y2(a), значит а-абсцисса точки пересечения
Крылов 4282
Слайд 9Шаг 3.
В цикле рассматриваем каждый участок нашего разбиения и ищем
точки пересечения функций:
while x
ffd=sin(x+d)-sqrt(x+d)+3; fffd=cos(x+d)-sqrt(x+d)+3; if f*fd<0 c=c+1; end;
if ff*ffd<0 cc=cc+1; end;
if fff*fffd<0 ccc=ccc+1; end; x=x+d;
end;
Крылов 4282
Слайд 10Шаг 4.
Ищем наибольшее из чисел с сс ссс:
if c>cc
if c>ccc
max=c;
else max=ccc;
end;else if cc>ccc
max=cc;
else max=ccc;
end; end;
Крылов 4282
Слайд 11Шаг 5.
Построение графиков:
x=b:0.001:a;
gf=sin(x); gff=cos(x);
gfff=sqrt(x)-3;
hold on;
plot(x,gf,'color','black','LineWidth',2)
plot(x,gff,'color','cyan','LineWidth',2)
plot(x,gfff,'color','magenta','LineWidth',2)
xlabel('x'); ylabel('y');
Крылов 4282
Слайд 14Вывод:
Была изучена среда программирования Matlab, реализован алгоритм позволяющий находить число
точек пересечений функций на интервале. Построены графики функций в Matlab
и Excel, не отличающиеся друг от друга, и говорящие о правильности выполнения поставленной цели.Крылов 4282
