Слайд 2Литература
Основная литература.
Леоненков А. Нечеткое моделирование в среде MATLAB и fuzzyTECH.
СПб: БХВ-Петербург. 2003. - 736с.
Кофман А. Введение в теорию нечетких
множеств.- М.: Радио и связь, 1982.- 432 с.
Орловский С.А. Проблемы принятия решений при нечеткой информации.- М.:Наука, 1981.- 206 с.
Борисов А.Н., Алексеев А.В., Меркурьева Г.В. и др. Обработка нечеткой информации в системах принятия решений.- М: Радио и связь. 1989. - 304 с.
Дополнительная литература.
Заде Л.А. Понятие лингвистической переменной и его применение к принятию приближенных решений.-М.:Мир, 1976.-165 с.
Поспелов Д.А. Ситуационное управление: теория и практика.- М. Наука, 1986.- 288 с.
Мелихов А.Н., Берштейн Л.С., Коровин С.Я. Ситуационные советующие системы с нечеткой логикой.- М.: Наука, 1990.- 272 с.
Слайд 3
Традиционные математические методы предназначены для обработки точных данных, таких как
«скорость автомобиля v = 111 км/ч». Представить такие данные графически
можно с использованием так называемых одноточечных (одноэлементных) множеств (рис. 1.1).
Слайд 4
Точные данные могут быть получены только с помощью высокоточных технических
измерительных устройств, в то время как человек способен непосредственно оценивать
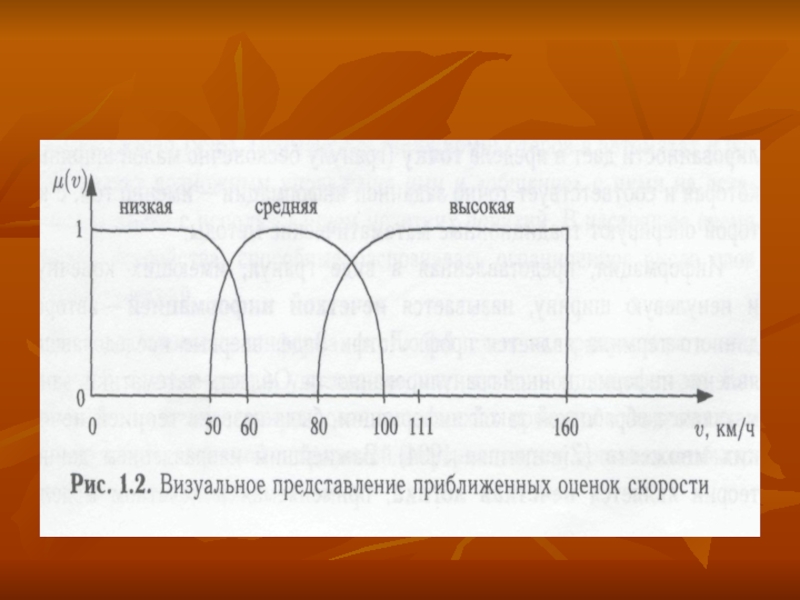
скорость автомобиля, оперируя такими терминами, как «низкая», «средняя» и «высокая». Эти приближенные оценки также можно представить графически (рис. 1.2).
Слайд 6
С помощью функций «низкая», «средняя» и «высокая», называемых функциями принадлежности,
можно определить, является ли некоторое точное значение скорости соответственно низким,
средним или высоким. Человек, наблюдающий автомобиль, движущийся со скоростью v = 111 км/ч, не в состоянии оценить это значение точно, но приближенно он может оценить такую скорость как высокую (рис. 1.2).
Слайд 7
О подобного рода оценках говорят как об информационных гранулах (Zadeh
1979,1996). Если трех гранул («низкая», «средняя», «высокая») недостаточно, точность оценки
скорости можно повысить, введя, например, 5 гранул — «очень низкая», «низкая», «средняя», «высокая», «очень высокая».
Точность оценки можно, наоборот, снизить, если использовать только две гранулы — «низкая» и «высокая». Степень гранулированности информации будет определяться потребностями и интеллектуальными способностями использующего ее человека, либо будет зависеть от контекста, в котором он ее использует.
Информация, получаемая от человека, обычно менее точна (более гранулирована), в то время, как информация от измерительных устройств является более точной (менее гранулированной).
Слайд 8
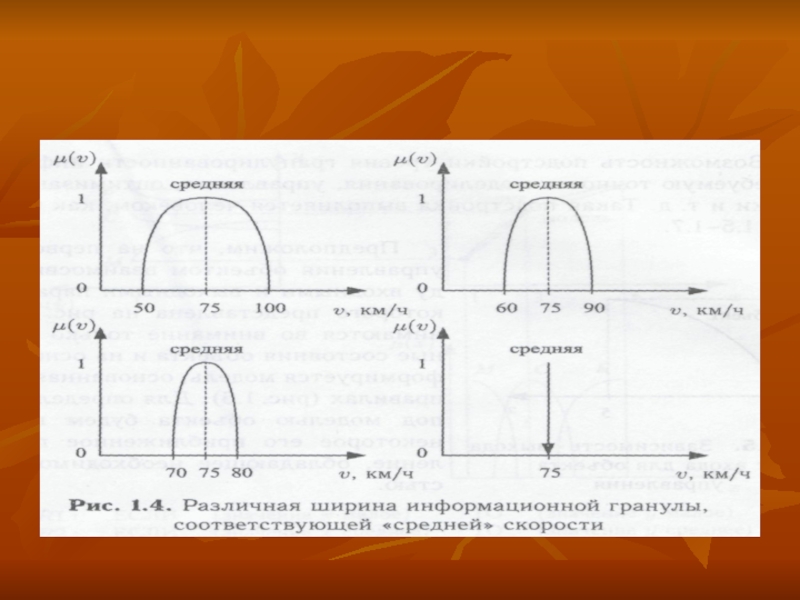
Гранулированность информации можно определить с помощью ширины гранулы (функции принадлежности),
и таким образом гранула «средняя» может иметь различную ширину, зависящую
от общего количества используемых человеком гранул (рис. 1.4). Как видно из рис. 1.4, уменьшение степени гранулированности дает в пределе точку (гранулу бесконечно малой ширины), которая и соответствует точно заданной информации — именно той, с которой оперируют традиционные математические методы.
Информация, представленная в виде гранул, имеющих конечную и ненулевую ширину, называется нечеткой информацией — автором данного термина является проф. Лотфи Заде, впервые исследовавший явление информационной гранулированности. Область математики, занимающаяся обработкой такой информации, была названа теорией нечетких множеств. Важнейшим направлением данной теории является нечеткая логика.
Слайд 10
Человек использует нечеткие множества для оценки и сравнения физических величин,
состояний объектов и систем на приближенном, качественном уровне. Так, любой
из нас способен оценить величину температуры, не прибегая к помощи термометра, а руководствуясь лишь собственными ощущениями и шкалой приближенных оценок, подобной тем, которые представлены на рис. 2.1.
Отметим, что качественная оценка имеет нечисловой характер, поскольку не обладает свойством аддитивности, присущим числам.
Пример. 1 см + 1 см = 2 см, но: небольшая сумма денег + небольшая сумма денег =? Результат подобной операции не всегда будет соответствовать большой сумме денег.
Понятия «небольшой» и «большой» суммы являются нечеткими и субъективными и зависят от смысла, вкладываемого в них в каждом конкретном случае. Поэтому качественные оценки нельзя складывать подобно тому, как это делается с числовыми величинами.
Слайд 12
• Лингвистическая переменная
Лингвистической переменной является переменная (которая может быть как
входной или выходной, так и переменной состояния) с лингвистическими значениями,
выражающими качественные оценки.
Примеры: скорость судна, электрическое напряжение, температура.
На практике для задания лингвистических переменных можно использовать не только лингвистические значения, но и нечеткие числа (Bertram 1994; Koch 1993), т. е. определенного рода комбинированный подход.
Слайд 13
• Лингвистическое значение
Лингвистическое значение представляет собой значение лингвистической переменной,
выраженное в словесной форме.
Примеры: очень большой отрицательный, средний отрицательный, средний
положительный, очень большой положительный, старый, молодой, хороший, средний, приятный, неприятный, истинный, ложный.
Лингвистическое значение всегда присутствует в модели совместно со связанной с ним лингвистической переменной.
Слайд 14
Нечеткие числа
Примеры нечетких чисел: около нуля, примерно 5, более (менее)
5, немного более 9, приблизительно между 10 и 12.
Оценка параметров
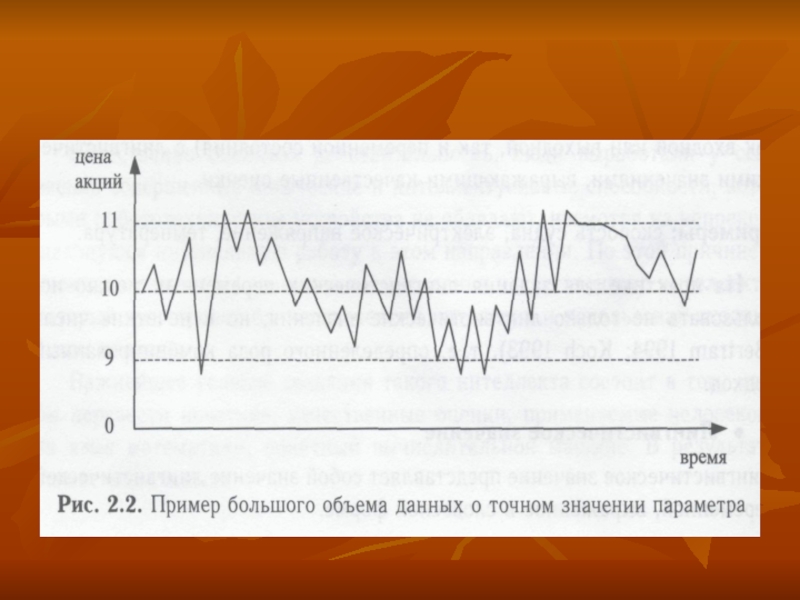
системы с использованием лингвистических значений основана на восприятии человека и не требует технических измерительных устройств, в то время как при использовании с этой целью нечетких чисел подобные устройства необходимы. С помощью нечетких чисел можно обобщать большие объемы точных данных, являющихся результатами измерений или обращений к базам данных, например информацию о цене Xi на акции некоторой компании (рис. 2.2).
Слайд 16
• Мощность числовой области значений
Мощность числовой области значений (числовой
предметной области) есть число содержащихся в ней элементов:
||Х||=n.
(2.1)
• Нечеткое множество
Нечетким множеством А, определенным на некоторой числовой предметной области X, называется множество пар:
А = {(μ*А(х), х)}, (2.2)
где для каждого элемента x степень μ*А его принадлежности множеству А задается с помощью функции принадлежности μА(х), при этом
[0,1].
Функция принадлежности отображает числовую область значений X данной переменной на отрезок [0,1]