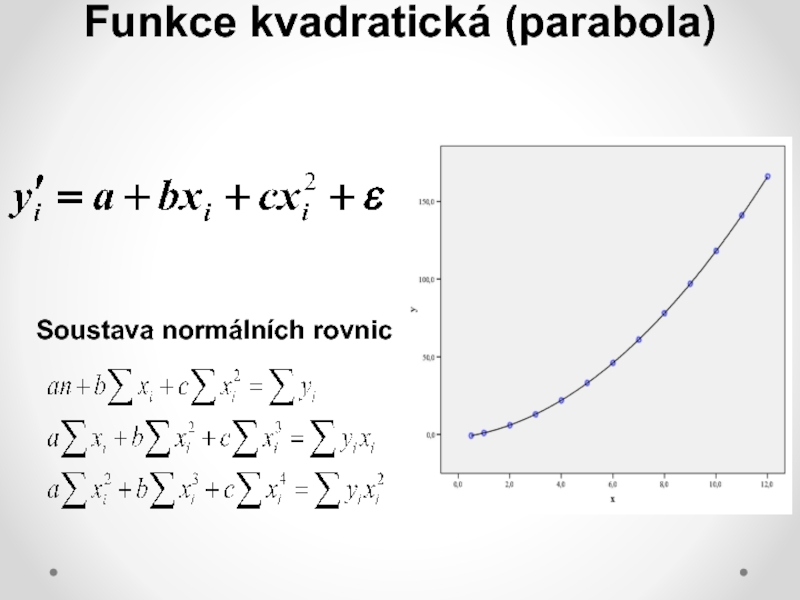
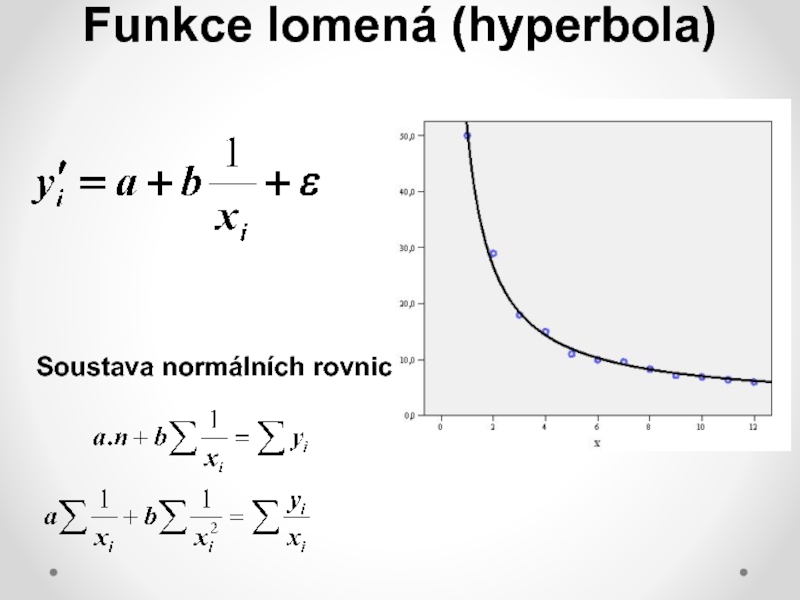
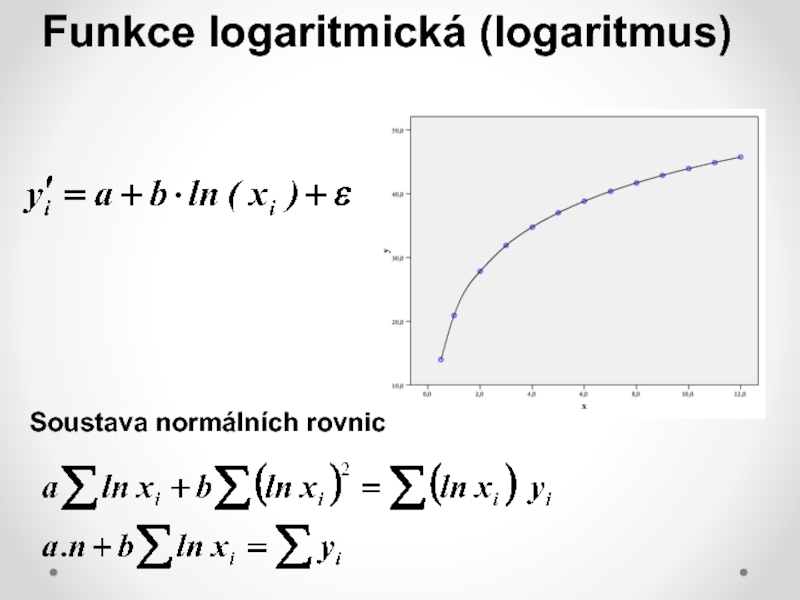
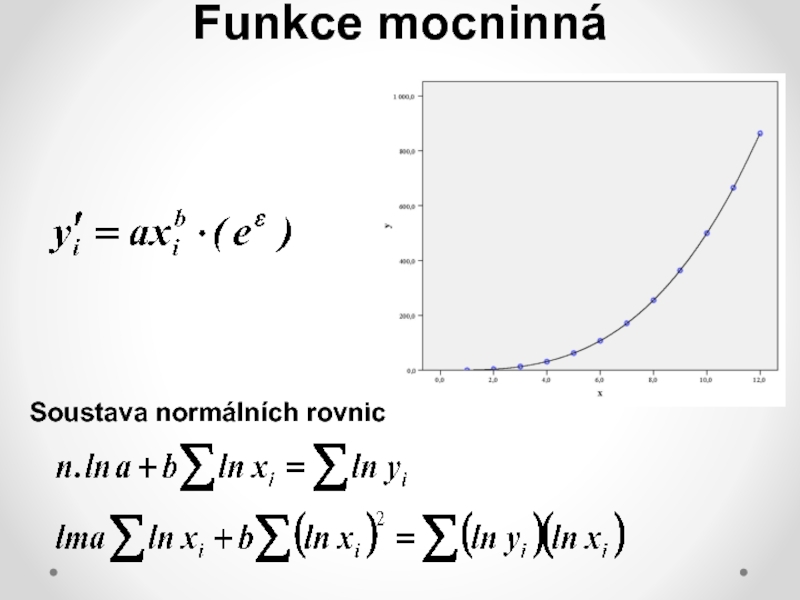
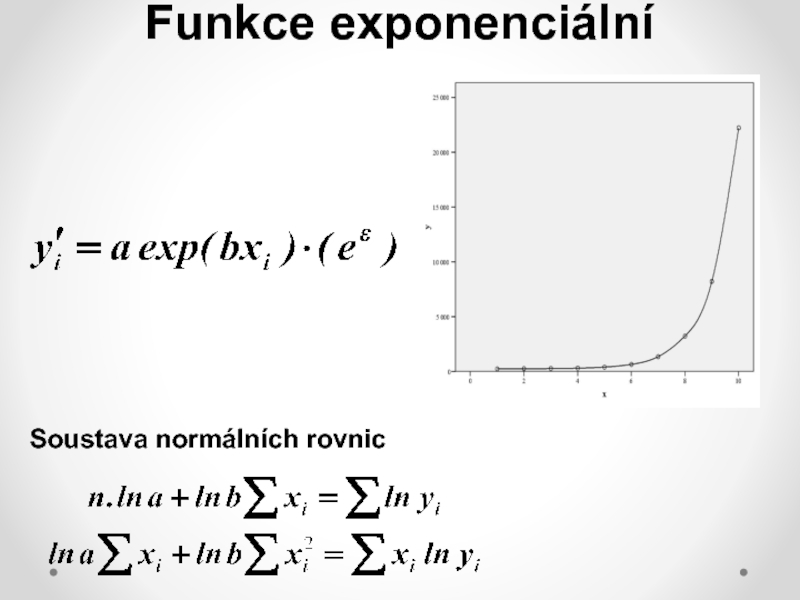
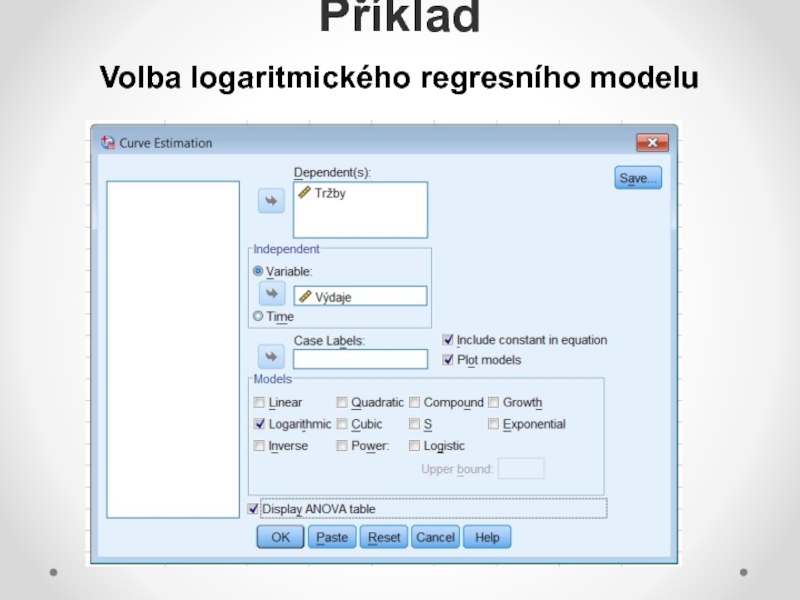
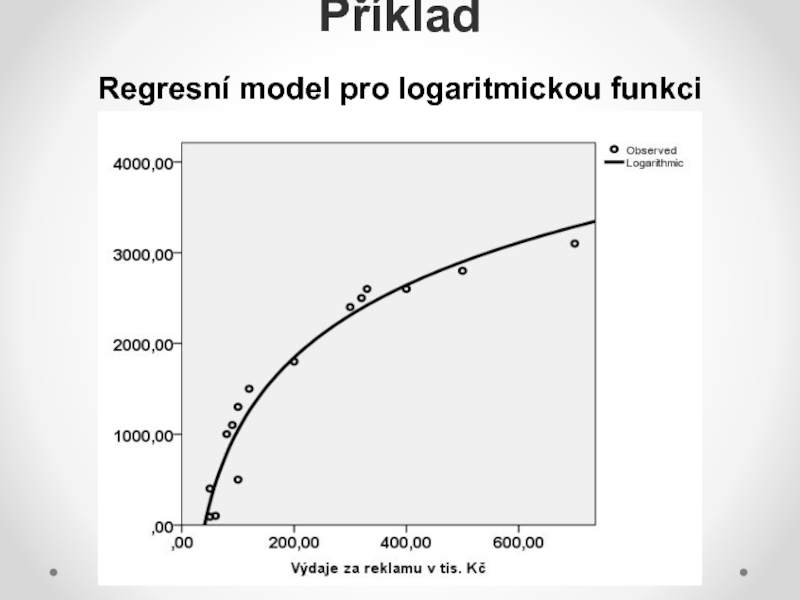
nelineárních modelů počítat s řadou komplikací:
neodhadnutelností některých parametrů,
existencí
minima funkce jen pro některé regresní modely, výskytem lokálních minim a sedlových bodů,
špatnou podmíněností parametrů v regresním modelu,
malým rozmezím experimentálních dat (zejména u parametrů vyjadřujících limitní chování modelu).