НЕЛИНЕЙНЫЙ ОСЦИЛЛЯТОР

в потенциальной яме
Фазовая плоскость
Период колебаний нелинейного осциллятора
Динамическая система общего вида

на фазовой плоскости. Особые точки и их классификация
Численное решение дифференциальных уравнений

НЕЛИНЕЙНЫЙ ОСЦИЛЛЯТОР

динамика которой описывается дифференциальным уравнением второго порядка:
В консервативном случае
В диссипативном

случае
Здесь x – динамическая переменная, о которой говорят как об обобщенной координате, f(x) — некоторая нелинейная функция, ϒ— параметр диссипации.

НЕЛИНЕЙНЫЙ ОСЦИЛЛЯТОР

m, которая может свободно двигаться вдоль оси x, причем трение

отсутствует.

НЕЛИНЕЙНЫЙ ОСЦИЛЛЯТОР

собой не что иное, как запись закона сохранения механической энергии.

Первый член отвечает кинетической энергии частицы, а второй — потенциальной энергии в поле внешней силы. Соответственно, функцию V(x) называют потенциальной функцией.

Если потенциальная функция имеет минимум (присутствует потенциальная яма), то вблизи дна этой ямы система может совершать колебания.

НЕЛИНЕЙНЫЙ ОСЦИЛЛЯТОР

минимум расположен в точке
Тогда разложение в ряд Тейлора вблизи этой

точки будет иметь вид (4.7)
Если ограничиться учетом квадратичного члена, то подстановка выражения (4.7) в


Это уравнение линейного гармонического осциллятора. Величина отвечает отклонению от точки минимума потенциальной ямы, а характеризует собственную частоту малых колебаний.

НЕЛИНЕЙНЫЙ ОСЦИЛЛЯТОР

фазовой плоскости. Динамику системы представляют, используя фазовые портреты — картинки

на фазовой плоскости, где изображены существенные для понимания поведения системы объекты.

движению. Следовательно, такая траектория представляет собой не что иное, как

фазовый портрет периодического колебательного процесса.
Закон сохранения энергии
Константа интегрирования Е называется полной энергией колебаний. Имеем:
Знак «+» в этом уравнении соответствует участкам фазовых траекторий, лежащим в верхней полуплоскости, знак «–» - в нижней. Разделяя переменные, получим

НЕЛИНЕЙНЫЙ ОСЦИЛЛЯТОР

в такой области Хmin≤Х≤Хmax, что в ней U(x)≤E, причем равенство

достигается на краях интервала, т.е. Хmin и Хmax представляют собой корни уравнения E=U(x); их называют точками поворота.

их классификация
НЕЛИНЕЙНЫЙ ОСЦИЛЛЯТОР
(4.19)

Мгновенное

состояние такой системы определяется заданием двух переменных, X=X0 и Y=Y0.
Геометрически мгновенное состояние представляется точкой на фазовой плоскости (x, y), а эволюция состояния во времени соответствует движению этой изображающей точки по некоторой кривой – фазовой траектории.
Когда говорят о динамической системе с двумерным фазовым пространством, ее часто обозначают для краткости терминами двумерная система или динамическая система на плоскости.

их классификация
НЕЛИНЕЙНЫЙ ОСЦИЛЛЯТОР
Вычислив правые части уравнений (4.19) в некоторой точке

фазовой плоскости (x,y) получаем два числа, f(x,y) и g(x,y) - компоненты вектора скорости движения изображающей точки по фазовой плоскости в тот момент, когда она имеет соответствующие координаты (x,y).
Поскольку каждой точке фазовой плоскости отвечает определенный вектор скорости, то можно утверждать, что с нашей динамической системой ассоциируется определенное векторное поле на плоскости.
Вектор, отвечающий каждой точке, задает в этой точке определенное направление. Поэтому говорят также о поле направлений на плоскости, ассоциирующемся с данной динамической системой.
Изоклины - вспомогательные кривые на ФП, каждая из которых соответствует определенному фиксированному направлению векторного поля. (Метод изоклин).

их классификация
НЕЛИНЕЙНЫЙ ОСЦИЛЛЯТОР



Каждая пара (X0, Y0), удовлетворяющая этой системе уравнений,

соответствует некоторой особой точке на фазовой плоскости.
Отличительные особенности особой точки:
в особой точке не определено направление векторного поля, так как модуль вектора равен нулю;
множество состояний, посещаемых системой в процессе временной эволюции с начальным условием, отвечающем особой точке, состоит из одной этой точки.
С физической точки зрения, особые точки соответствуют стационарным режимам динамики или состояниям равновесия системы. Их называют также неподвижными точками.

их классификация
НЕЛИНЕЙНЫЙ ОСЦИЛЛЯТОР
Имея представление о свойствах каждого выделенного типа особых

точек и о том, какие из них присутствуют на фазовой плоскости интересующей нас динамической системы, можно делать выводы об устройстве фазового пространства и о характере возможных в этой системе колебательных процессов.

Пусть (X0, Y0) — особая точка системы. Будем искать близкое к особой точке, зависящее от времени решение в виде

их классификация
НЕЛИНЕЙНЫЙ ОСЦИЛЛЯТОР





Матрица Якоби
Применим экспоненциальную подстановку. Зависимость добавок от времени

имеет вид

их классификация
НЕЛИНЕЙНЫЙ ОСЦИЛЛЯТОР
Для вычисления собственных чисел матрицы

можно воспользоваться тем обстоятельством, что след матрицы(сумма диагональных элементов) . равен сумме собственных чисел, а детерминант — их произведению.

их классификация
НЕЛИНЕЙНЫЙ ОСЦИЛЛЯТОР
Общее решение дифференциального уравнения, описывающего эволюцию во времени

малых возмущений особой точки, записывается в виде линейной комбинации двух членов, пропорциональных, соответственно, и .
Если оба собственных числа отрицательны, то возмущение с течением времени затухает и стремится к нулю, т.е. система приближается к особой точке. Это устойчивая особая точка.
Если хотя бы одно собственное больше нуля, то соответствующая составляющая возмущение будет нарастать, т.е. система будет уходить от особой точки. Следовательно, это неустойчивая особая точка.

их классификация
НЕЛИНЕЙНЫЙ ОСЦИЛЛЯТОР

Зависимость возмущений от времени в этом случае определяется

выражением вида
λ′ - действительная, а λ ′′ – мнимая часть собственного числа.
Особая точка устойчива, если действительная часть λ′<0, и неустойчива, если λ′ >0.
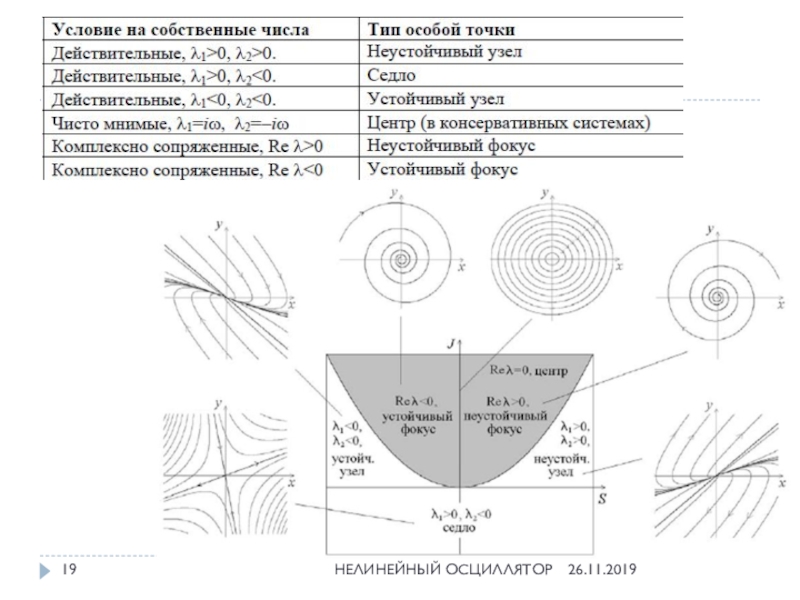
Таким образом, характер поведения фазовых траекторий и, следовательно, вид фазового портрета в окрестности особой точки, определяется собственными числами λ1 и λ2, а они выражаются через след и детерминант матрицы Якоби, S и J.

их классификация
НЕЛИНЕЙНЫЙ ОСЦИЛЛЯТОР
Внутренние точки показанных областей представляют типичные ситуации. Ситуаций,

реализующиеся на границах областей, на данном этапе считаются как атипичные или негрубые.
Особую роль на диаграмме играет линия S=0 (консервативные системы). В таких системах встречается особая точка типа центр, в окрестности которой фазовые траектории имеют вид вложенных друг в друга замкнутых кривых. Для диссипативных систем это не характерно.

что фигурирующие в правых частях функции могут зависеть не только

от динамических переменных, но и от времени
Будем представлять искомые функции времени x(t) и y(t) их значениями на дискретном множестве точек tn=nh, как говорят, в узлах сетки с шагом h по времени:

От величины шага зависит точность решения.

времени и состоит в том, чтобы положить
Запись уравнений в виде

разностной схемы:



Используя эти соотношения и задавшись начальными условиями (X0, Y0), мы можем шаг за шагом вычислять на компьютере значения переменных в узлах сетки n=1,2,3,…

получить таблицу функций, представляющих решение;
вывести на дисплей в виде графика

временной зависимости, откладывая по оси абсцисс время tn=nh, а по оси ординат значения Xn и Yn;
вывести на дисплей в виде фазового портрета, откладывая по оси абсцисс значения Xn, а по оси ординат Yn.

при аппроксимации производных выражениями (4.33) мы допускаем на каждом шаге

ошибку порядка h^2. Поскольку число шагов при построении решения порядка h^-1, а ошибка имеет тенденцию накапливаться от шага к шагу, результирующая погрешность будет порядка h, т.е. шаг в первой степени. Поэтому в данном случае мы имеем разностный метод первого порядка. Его называют методом Эйлера.
Повышение точности. Выполним сначала, используя метод Эйлера, половину шага и найдем

Затем, отправляясь от исходной точки, сделаем полный шаг, но с использованием поправленных величин при вычислении функций. Имеем:

метод второго порядка

превратилась в настоящее время в самостоятельный обширный раздел вычислительной математики.

Наряду с перечисленными здесь методами существует множество других, которые в каких-то случаях могут оказаться удобными (например, многошаговые схемы Адамса).