не имеют, а при a > 0 равносильны двойному неравенству
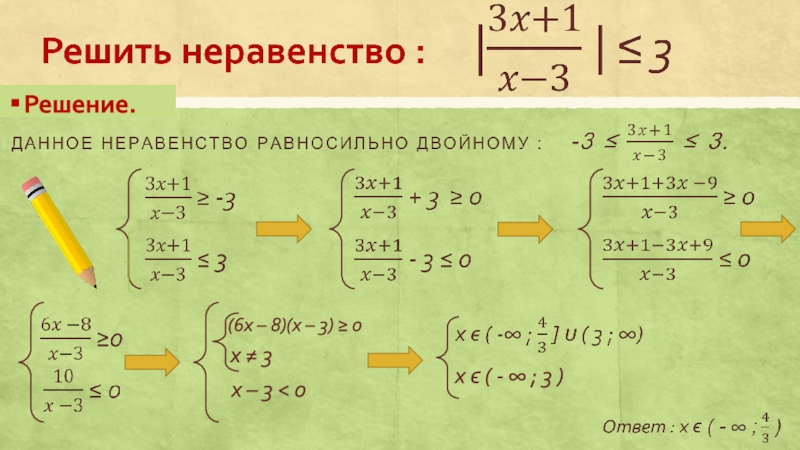
–a < f(x) < a. Заметим, что если неравенство нестрогое |f(x) |≤ a, то при а=0 оно равносильно уравнению f(x)=0.Неравенства вида |f(x)| > a при a ≤ 0 имеют решением всю область определения функции f(x). При a > 0 исходное неравенство равносильно двум неравенствам : f(x) > a и f(x) < -a, при этом решения обоих неравенств являются решениями исходного. Это справедливо и для нестрогих неравенств.





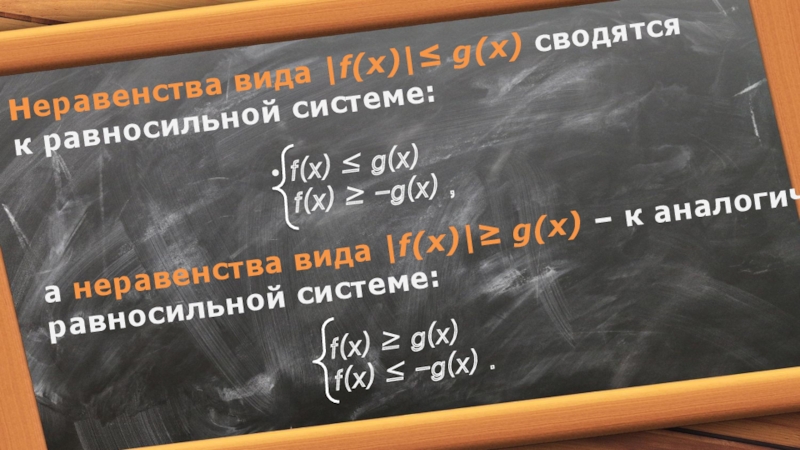







![Неравенства с модулями Неравенства вида |f(x)|>|g(x)|, как и соответствующие уравнения, сводятся к равносильному Неравенства вида |f(x)|>|g(x)|, как и соответствующие уравнения, сводятся к равносильному [ f(x) ]2 > [](/img/tmb/6/597997/0e966127088e61e7107bf2eacbc187ca-800x.jpg)