Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Нестандартные способы умножения чисел
Содержание
- 1. Нестандартные способы умножения чисел
- 2. «Предмет математики настолько серьезен, что полезно не упускать случаев делать его немного занимательным».Блез Паскаль
- 3. Цель:Изучить нестандартные способы умножения чисел, не используемых на уроках, и их применение при вычислениях числовых выражений.
- 4. Задачи:Найти и разобрать различные способы умножения.Рассказать о
- 5. Методы: поисковый метод с использованием научной и
- 6. Старинный способ умножения на 9 на пальцах 9∙3 = ?
- 7. Древнерусский способ умножения на 6,7,8,9 на пальцахДревнерусский
- 8. Теперь попробуем умножить, например, 7х8. Для этого
- 9. Пальцы левой руки, оставшиеся сверху, умножаем на
- 10. Русско-крестьянский способ умноженияСущность этого способа в том,
- 11. Китайский способ умноженияСуть этого метода состоит в
- 12. Японский способ умноженияЯпонский способ умножения – это
- 13. Итальянский способ умножения («Сеткой»)Итальянский способ умножения был
- 14. ТАБЛИЦА УМНОЖЕНИЯ в стихах Ученики и ученицы!Чтоб было
- 15. Как быстро умножать на 11? Просуммируй первую и
- 16. Интересное число 37 Число 37 обладает многими любопытными
- 17. Список используемой литературы и Интернет-ресурсов1. Гарднер М.
- 18. Спасибо за внимание!
- 19. Скачать презентанцию
«Предмет математики настолько серьезен, что полезно не упускать случаев делать его немного занимательным».Блез Паскаль
Слайды и текст этой презентации
Слайд 2«Предмет математики настолько серьезен, что полезно не упускать случаев
делать его немного занимательным».
Блез Паскаль
Слайд 3Цель:
Изучить нестандартные способы умножения чисел, не используемых на уроках, и
их применение при вычислениях числовых выражений.
Слайд 4Задачи:
Найти и разобрать различные способы умножения.
Рассказать о новых способах умножения
и научить ими пользоваться учащихся.
Развить навыки самостоятельной работы: поиск
информации, отбор и оформление найденного материала.Слайд 5Методы:
поисковый метод с использованием научной и учебной литературы, а
также поиск необходимой информации в сети Интернет;
практический метод выполнения вычислений
с применением нестандартных алгоритмов счета;исследовательский метод при определении способов умножения.
Слайд 7Древнерусский способ умножения на 6,7,8,9 на пальцах
Древнерусский способ умножения на
пальцах является одним из наиболее употребительных методов, которым успешно пользовались
на протяжении многих столетий российские купцы. Они научились умножать на пальцах однозначные числа от 6 до 9. Каждому пальцу на левой и на правой руке приписывается определенное число:мизинцу - 6
безымянному пальцу – 7
среднему – 8
указательному – 9
большому – 10.
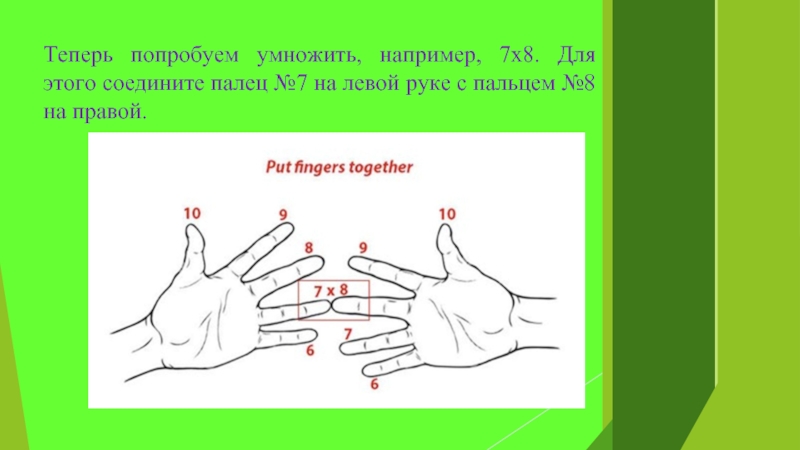
Слайд 8Теперь попробуем умножить, например, 7х8. Для этого соедините палец №7
на левой руке с пальцем №8 на правой.
Слайд 9Пальцы левой руки, оставшиеся сверху, умножаем на пальцы правой –
это и будут наши единицы (3х2=6). Сумма соединенных пальцев и
тех, что остались снизу – это будут десятки (2+3 = 5). Итог равен 56.Слайд 10Русско-крестьянский способ умножения
Сущность этого способа в том, что умножение любых
двух чисел сводится к ряду последовательных делений одного числа пополам
при одновременном удвоении другого числа. Деление пополам продолжают до тех пор, пока в частном не получится 1, при этом параллельно удваивают другое число. Последнее удвоенное число и даёт искомый результат.Слайд 11Китайский способ умножения
Суть этого метода состоит в том, что при
умножении чисел считаются точки пересечения прямых, которые соответствуют количеству цифр
каждого разряда обоих множителей.Пример: умножим 21 на 13.
Слайд 12Японский способ умножения
Японский способ умножения – это графический способ с
использованием кругов и линий. Не менее забавный и интересный чем
китайский. Даже чем-то на него похож.Пример: умножим 13 на 24
Слайд 13Итальянский способ умножения («Сеткой»)
Итальянский способ умножения был распространен в средние
века на Востоке и Италии. Пусть нужно умножить 25х63. Надо
начертить таблицу, в которой две клетки по длине и две- по ширине. Запишем одно число по длине таблицы, другое по ширине таблицы. В клетках — результаты умножения данных чисел, на их пересечении отделим десятки и единицы диагональю. Полученные цифры сложим по диагонали. Полученный результат можно прочитать по стрелке (вниз и вправо).Слайд 14ТАБЛИЦА УМНОЖЕНИЯ
в стихах
Ученики и ученицы!
Чтоб было проще вам считать,
Мы
Пифагорову таблицу
В стихах решили написать.
По ней легко найти решенье,
Куплет достаточно
прочесть,А чтоб запомнить вычисленья,
Везде своя подсказка есть!
Слайд 15Как быстро умножать на 11?
Просуммируй первую и вторую цифру числа,
которое собираешься умножать на 11, и поставь сумму цифр посередине.
Получившееся число из трёх цифр и есть результат. В случае если сумма цифр окажется больше 10, например 14, то прибавь 1 к первой цифре, а 4 ставь посередине. Вот примеры, по котором всё станет ясно:25 x 11 = 2 (2+5) 5 = 275, 34 x 11 = 3 (3+4) 4 = 374, 48 x 11 = 4 (4+8) 8 = 4 (12) 8 = (4+1) (2) 8 = 528.
Слайд 16Интересное число 37
Число 37 обладает многими любопытными свойствами. Так, умноженное
на 3 и на числа, кратные 3 (до 27 включительно),
оно дает произведения, изображаемые одной какой-либо цифрой:37 × 3 = 111; 37 × 6 = 222; 37 × 9 = 333; 37 × 12 = 444; 37 × 15 = 555; 37 × 18 = 666; 37 × 21 = 777; 37 × 24 = 888; 37 × 27 = 999.
Слайд 17Список используемой литературы и Интернет-ресурсов
1. Гарднер М. Математические чудеса и
тайны. – М.: Наука, 1986.
2. Корнеев А.А. Феномен русского умножения.
История. http://numbernautics.ru/3. Л.Ф. Магницкий «Арифметика», www.newlibrary.ru › НАУКА › МАТЕМАТИКА
4. nsportal.ru/ap/library
5. infourok.ru/material.
6. Энциклопедия для детей «Математика». – М: Аванта+, 2005.
Теги