Слайд 1Несжимаемая жидкость.
Уравнение Бернулли
Слайд 2Динамика жидкости
При изучение и описание движения жидкостей возможно два подхода.
Первый- следить за отдельной частицами например красителя. Второй- следить не
за движением частиц самой жидкости, а за точками
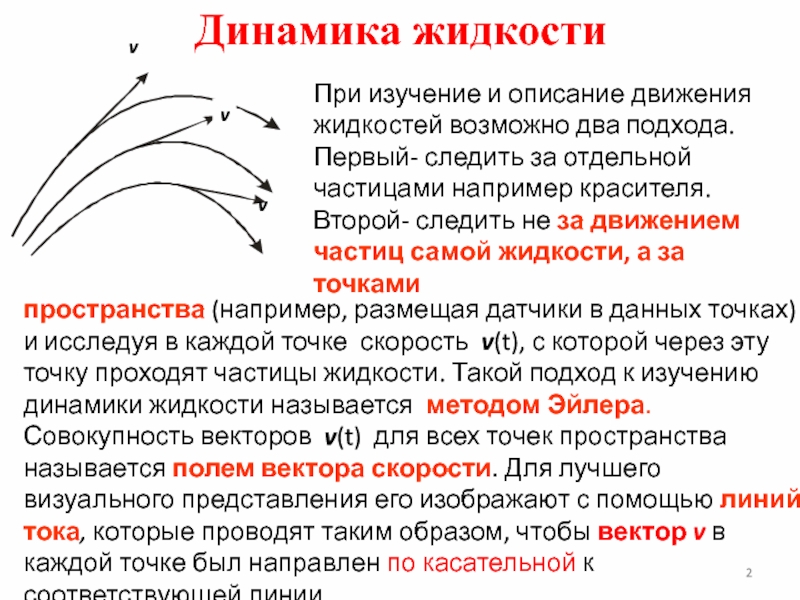
пространства (например, размещая датчики в данных точках) и исследуя в каждой точке скорость v(t), с которой через эту точку проходят частицы жидкости. Такой подход к изучению динамики жидкости называется методом Эйлера. Совокупность векторов v(t) для всех точек пространства называется полем вектора скорости. Для лучшего визуального представления его изображают с помощью линий тока, которые проводят таким образом, чтобы вектор v в каждой точке был направлен по касательной к соответствующей линии.
v
v
v
Слайд 3Динамика жидкости
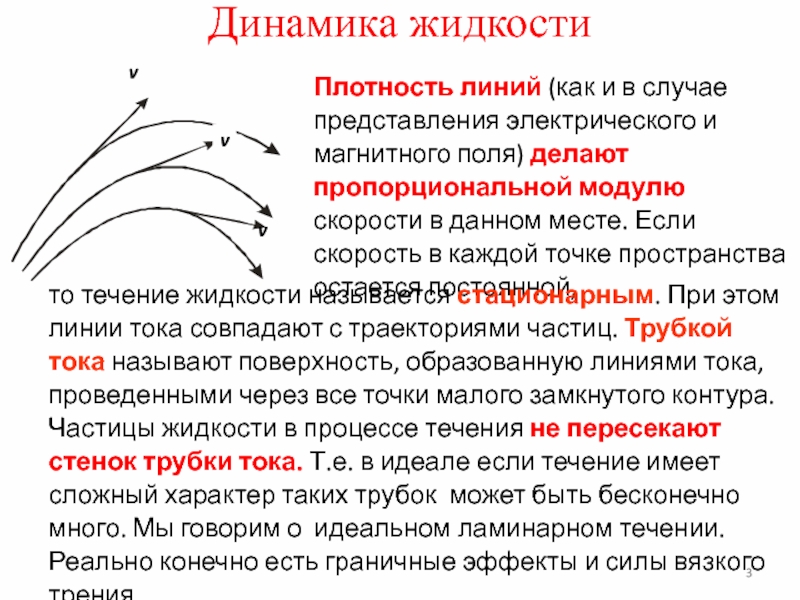
Плотность линий (как и в случае представления электрического и
магнитного поля) делают пропорциональной модулю скорости в данном месте. Если
скорость в каждой точке пространства остается постоянной,
то течение жидкости называется стационарным. При этом линии тока совпадают с траекториями частиц. Трубкой тока называют поверхность, образованную линиями тока, проведенными через все точки малого замкнутого контура. Частицы жидкости в процессе течения не пересекают стенок трубки тока. Т.е. в идеале если течение имеет сложный характер таких трубок может быть бесконечно много. Мы говорим о идеальном ламинарном течении. Реально конечно есть граничные эффекты и силы вязкого трения.
v
v
v
Слайд 4Модель несжимаемой жидкости
Несжимаемой жидкостью называется однородная жидкость постоянной плотности
(плотность постоянна в процессе изучения). Реально через каждое сечение трубки
тока за одно и то же время протекают одинаковые объемы идеальной жидкости. Для тонкой трубки тока, когда скорость частиц v в пределах поперечного сечения S постоянна за единицу времени протекает объем S v и можно записать:
S v = const
Это простое заключение, отражающее свойство несжимаемой жидкости при стационарном течении по трубке тока называется теоремой о неразрывности струи.
Проще: сколько втекло столько и вытекло!
Слайд 5Идеальная несжимаемая жидкость
Для жидкостей существует еще одна упрощающая модель –
модель идеальной жидкости. Идеальной называют жидкость, у которой внутреннее трение
между слоями полностью отсутствует. Реально оно конечно есть. Т.е. это такая же абстракция как и абсолютно твердое тело и идеальный газ.
Рассмотрим стационарное течение идеальной несжимаемой жидкости в однородном силовом поле притяжения Земли. Пусть за Δt объем жидкости между нормальными сечениями 1’ и 2’ сместится вниз (p1>p2) по трубке тока до сечений 1 и 2 (Δl1≠Δl2). Была совершена работа! На что израсходована? Какими силами?
Земля
F1
F2
h1
h2
F
F
∆l1
∆l2
S1
S2
2
2’
1
1’
Слайд 6Даниил Бернулли (29.1.1700- 17.3.1782), сын Иоганна Бернулли (брат - Якоб
Бернулли) . Занимался физиологией и медициной, но больше всего математикой
и механикой. В 1725-33 он работал в Петербургской АН сначала на кафедре физиологии, а затем механики. Впоследствии он состоял почётным членом Петербургской АН, опубликовал (с 1728-78) в её изданиях 47 работ. В работах, завершенных написанным в Петербурге трудом "Гидродинамика" (1738), вывел основное уравнение стационарного движения идеальной жидкости, носящее его имя. Даниил Бернулли разрабатывал кинетические представления о газах.После рассмотрения принципа Бернулли можно объяснить причины столкновения двух кораблей
Слайд 7Осенью 1912 г океанский пароход "Олимпик" плыл в открытом море,
а почти параллельно ему, на расстоянии сотни метров, проходил с
большой скоростью другой корабль, гораздо меньший, броненосный крейсер "Гаук". Когда оба судна заняли положение, изображенное на рисунке, произошло нечто неожиданное: меньшее судно стремительно свернуло с пути, словно повинуясь неведомой силе, повернулось носом к большому кораблю и, не слушаясь руля, двинулось почти прямо на него. "Гаук" врезался носом в бок "Олимпика".Удар был так силен, что "Гаук" проделал в борту "Олимпика" большую пробоину. Случай столкновения двух кораблей рассматривался в морском суде. Капитана корабля "Олимпик" обвинили в том, что он не дал команду пропустить броненосец.
Слайд 8Между двумя полосками бумаги продуваем воздух, они сближаются. Скорость воздуха
внутри полосок больше, значит давление между листами меньше, чем снаружи.
Парадоксальность результатов такого поведения тел можно объяснить, используя закон Берннули (уравнение Бернулли). Швейцарский ученый Даниил Бернулли длительное время жил в России, именно к этому времени относится создание его главного научного труда - теории гидромеханики. Основная теорема гидродинамики связывает давление жидкости с её скоростью.
Слайд 11Уравнение Бернулли: давление жидкости (или газа) больше там, где её
скорость меньше и наоборот.
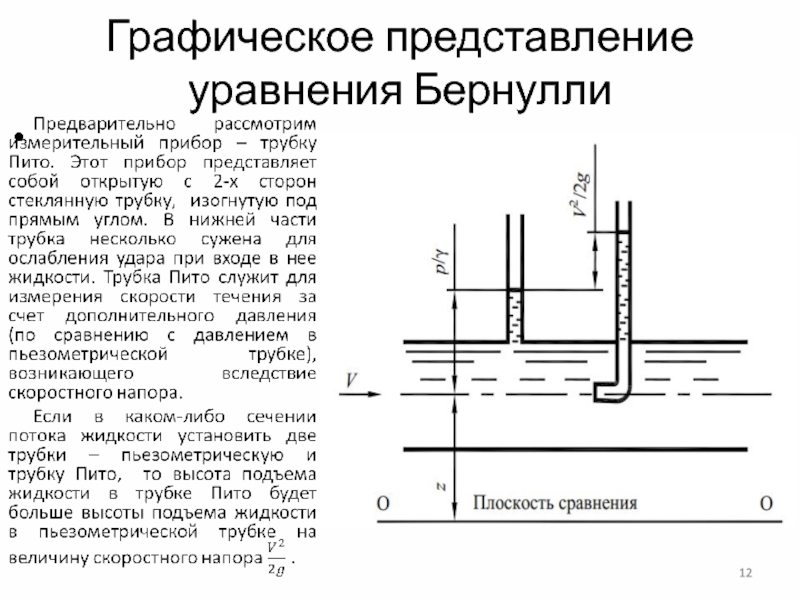
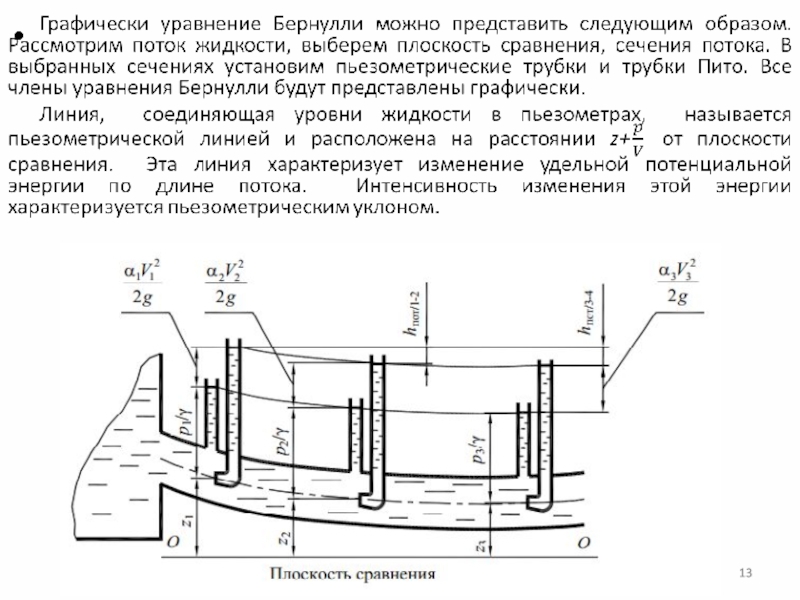
Слайд 12Графическое представление уравнения Бернулли
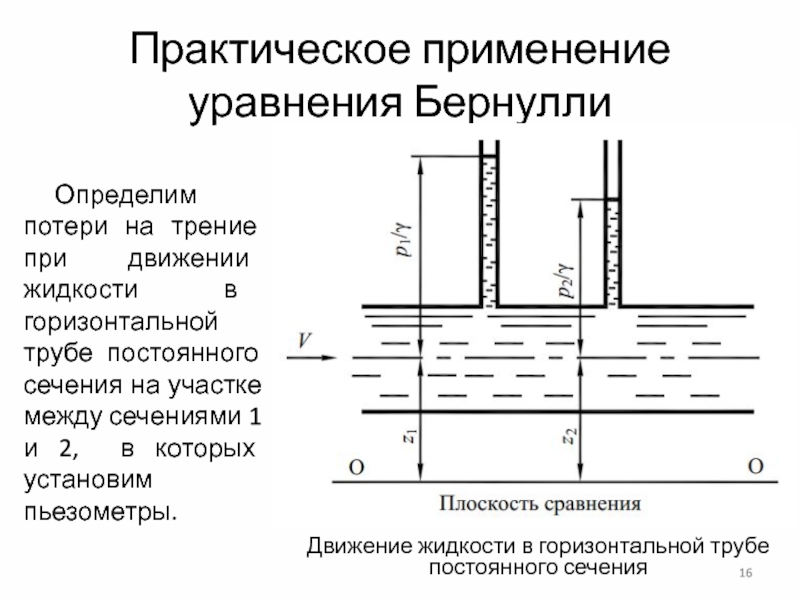
Слайд 16Практическое применение уравнения Бернулли
Движение жидкости в горизонтальной трубе постоянного сечения
Определим
потери на трение при движении жидкости в горизонтальной трубе постоянного
сечения на участке между сечениями 1 и 2, в которых установим пьезометры.
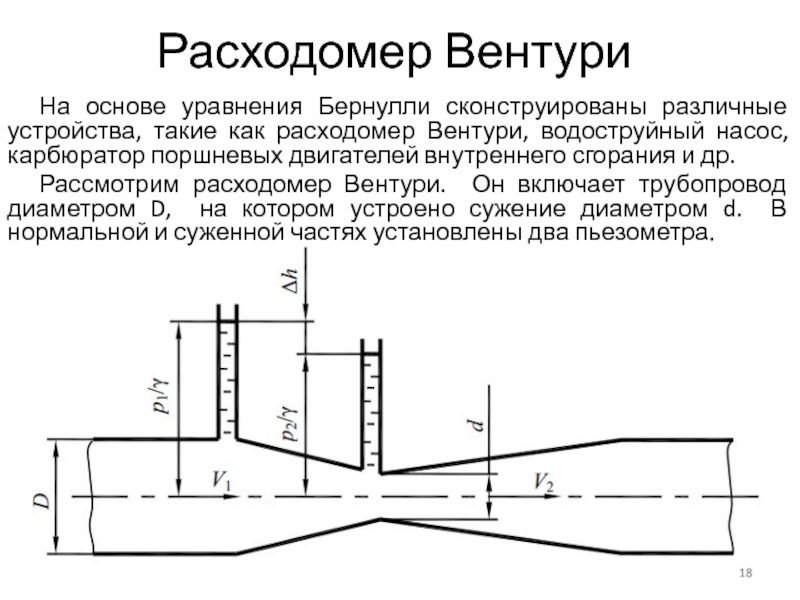
Слайд 18Расходомер Вентури
На основе уравнения Бернулли сконструированы различные устройства, такие как
расходомер Вентури, водоструйный насос, карбюратор поршневых двигателей внутреннего сгорания и
др.
Рассмотрим расходомер Вентури. Он включает трубопровод диаметром D, на котором устроено сужение диаметром d. В нормальной и суженной частях установлены два пьезометра.
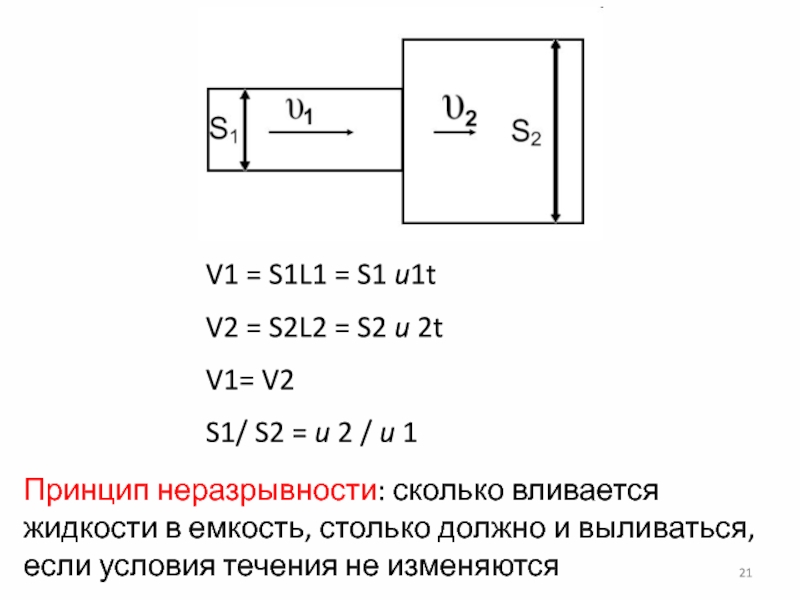
Слайд 21V1 = S1L1 = S1 u1t
V2 = S2L2 =
S2 u 2t
V1= V2
S1/ S2 = u 2 /
u 1
Принцип неразрывности: сколько вливается жидкости в емкость, столько должно и выливаться, если условия течения не изменяются
Слайд 22Практическое использование уравнения Бернулли
Основное уравнение гидродинамики—уравнение Бернулли — широко используется
в технической лабораторной практике для решения ряда гидравлических задач. Так,
например, уравнение Бернулли используется для гидравлических расчетов — напорных трубопроводов, насосных установок, гидравлических турбин, центрифуг, сепараторов и пр.
Принцип работы многих измерительных приборов и водоподъемных установок основан также на использовании уравнения Бернулли. Особенно широкое применение из числа таких приборов и установок получили приборы для измерения скоростей и расходов жидкости и водоструйные насосы (эжекторы, инжекторы).
Слайд 23Истечение жидкости через отверстия и сопла
Поток жидкости, протекающий через сужающееся
сопло, показан на рисунке, а. Общее увеличение скорости при прохождении
сужения сглаживает влияние любой неоднородности, которая может существовать в приближающемся потоке, поэтому разумно предположить, что в поперечном сечении истекающей струи распределение скоростей однородно. Так как поперечное сечение рассматриваемой струи равно поперечному сечению сопла, объемный расход жидкости может быть получен перемножением площади сопла на скорость истечения струи. На рис. b, с линии тока жидкости в месте истечения из отверстий не параллельны друг другу, а образуют сужающийся поток, т.е. поперечное сечение струи уменьшается до так называемого узкого сечения. За пределами этого сечения линии тока параллельны. Более того, "вниз" по потоку однородным будет и поле скоростей. Объемный расход в этом случае равен произведению площади потока в узком сечении на скорость жидкости за ним.
Слайд 24Примеры истечения струй из сопел и отверстий: a - параллельная
струя; b - суживающаяся струя из сопла; с - суживающаяся
струя из отверстия с острыми кромками
В каждом из трех примеров вытекающий поток показан в виде свободной струи, т.е. струи, которая не смешивается с окружающей жидкостью. Примером может служить истечение воды в воздух. Такие струи обычно сохраняют свою форму на значительном расстоянии, прежде чем распадаются в результате возмущений, вызывающих потерю устойчивости, особенно в случае отсутствия турбулентных пульсаций в потоке до его истечения. В случае, когда поток смешивается с окружающей жидкостью, образуется затопленная струя. Такая струя обычно становится турбулентной на небольшом расстоянии от узкого сечения. Она вовлекает в движение окружающую жидкость и быстро растворяется в ней. Независимо от этого объемный расход так же определяется произведением площади узкого сечения на скорость жидкости в нем.
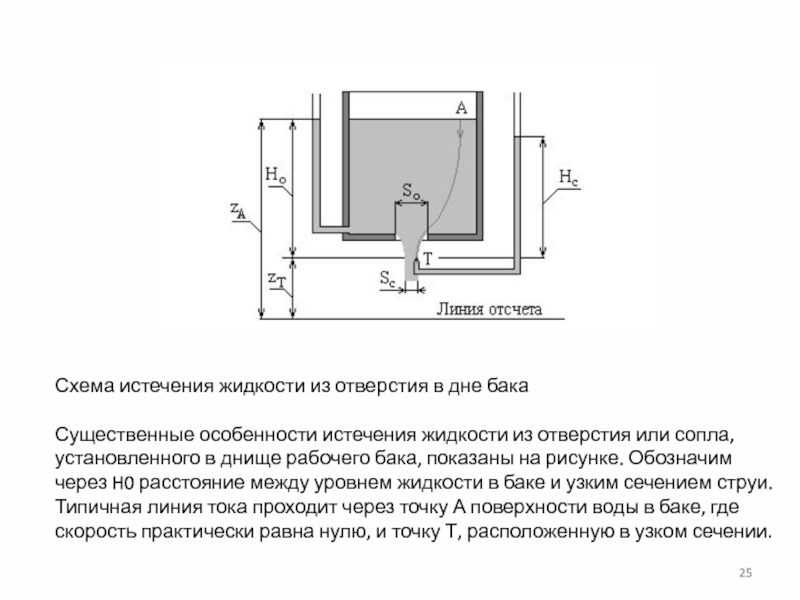
Слайд 25Схема истечения жидкости из отверстия в дне бака
Существенные особенности истечения
жидкости из отверстия или сопла, установленного в днище рабочего бака,
показаны на рисунке. Обозначим через H0 расстояние между уровнем жидкости в баке и узким сечением струи. Типичная линия тока проходит через точку А поверхности воды в баке, где скорость практически равна нулю, и точку Т, расположенную в узком сечении.