Низкомолекулярные аморфные материалы: структурные различия между жидкостью и

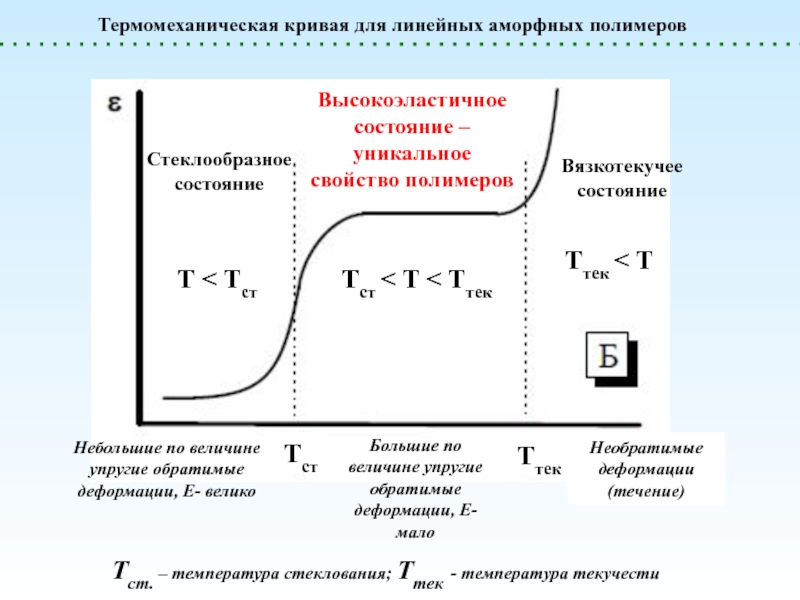
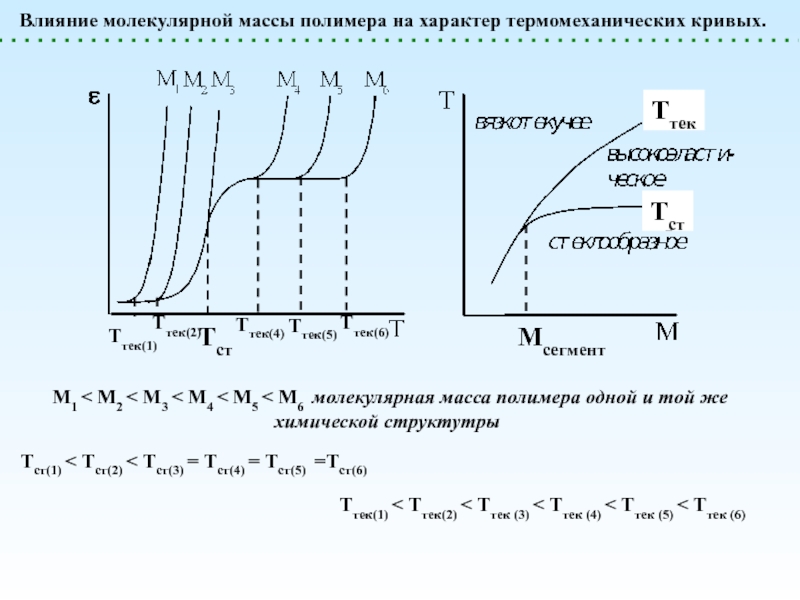
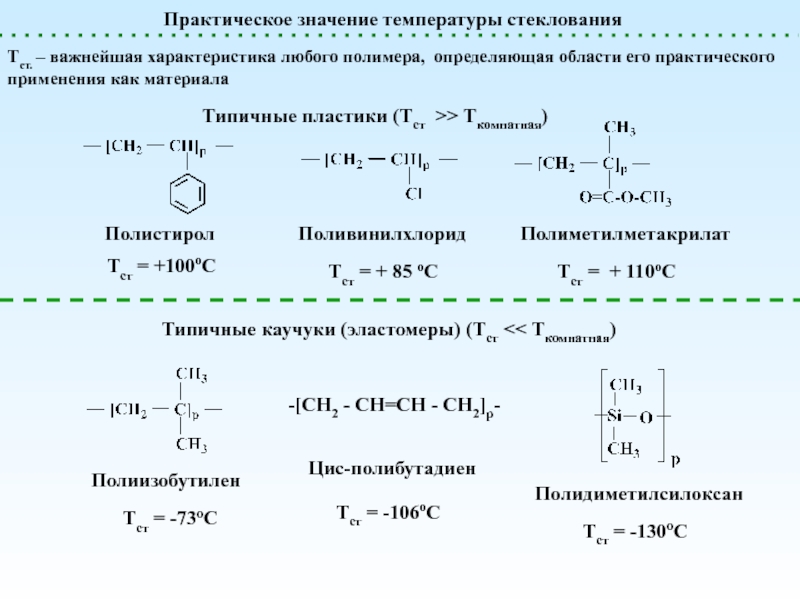
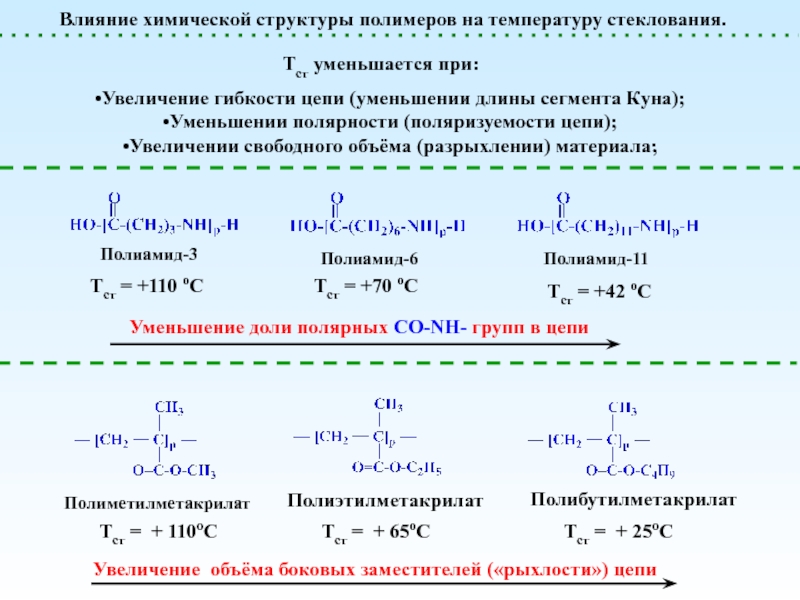
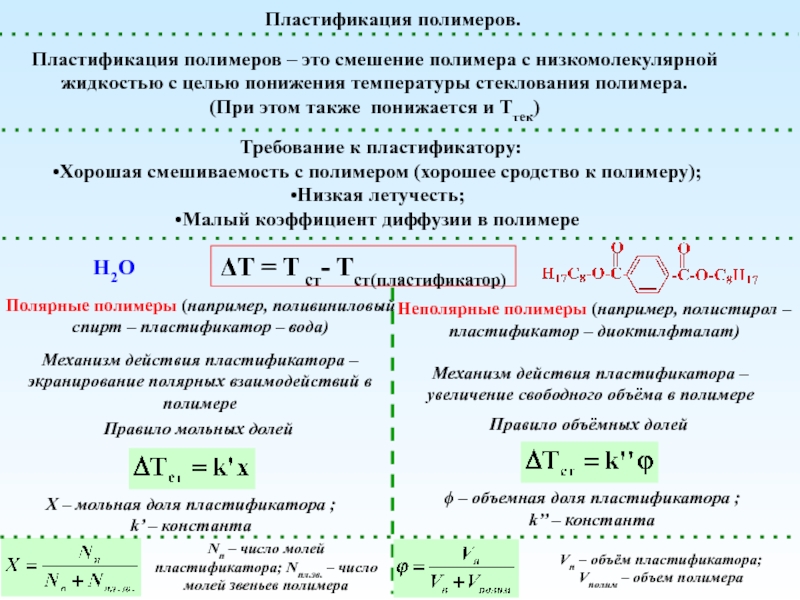
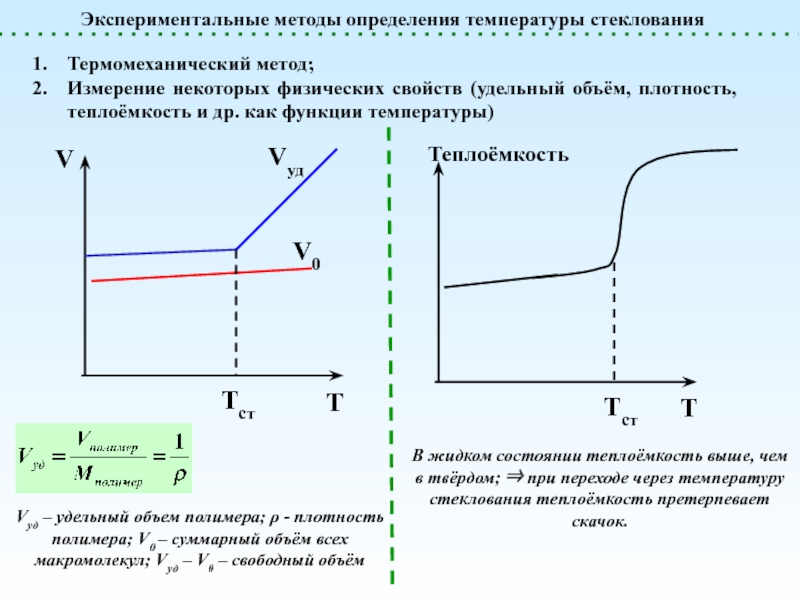
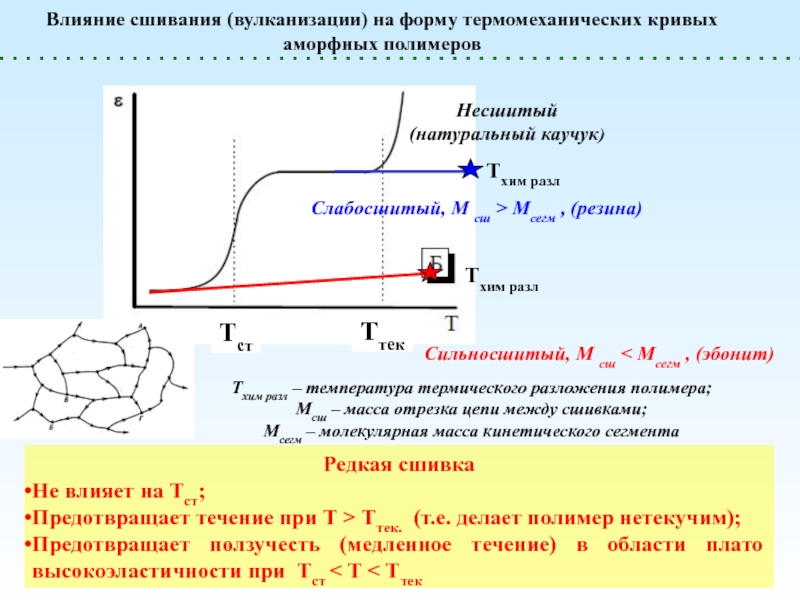
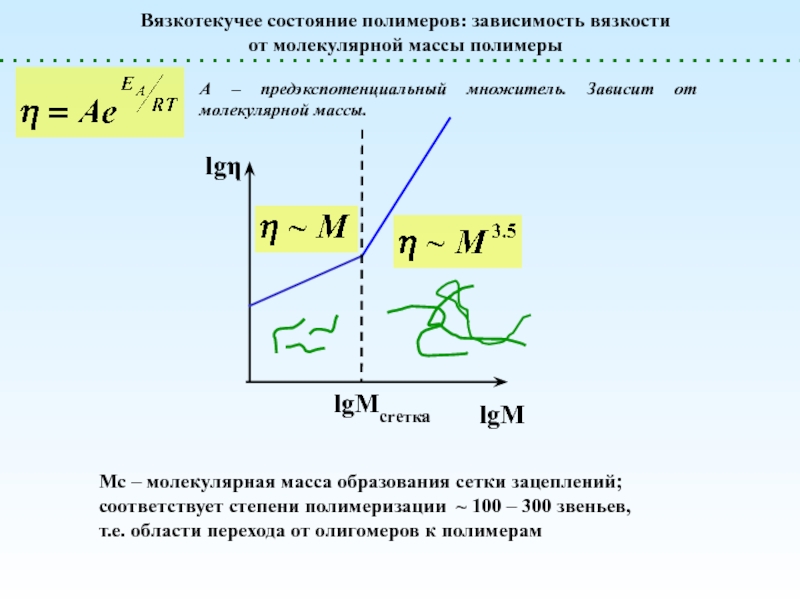
(стеклообразное)
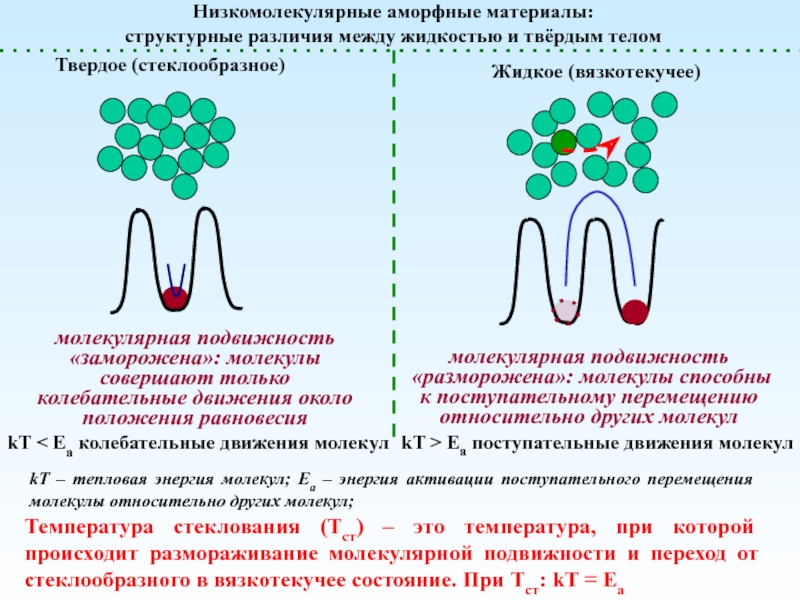
Жидкое (вязкотекучее)
kT < Еа колебательные движения молекул
kT > Еа поступательные

молекулярная подвижность «заморожена»: молекулы совершают только колебательные движения около положения равновесия

молекулярная подвижность «разморожена»: молекулы способны к поступательному перемещению относительно других молекул

kT – тепловая энергия молекул; Ea – энергия активации поступательного перемещения молекулы относительно других молекул;

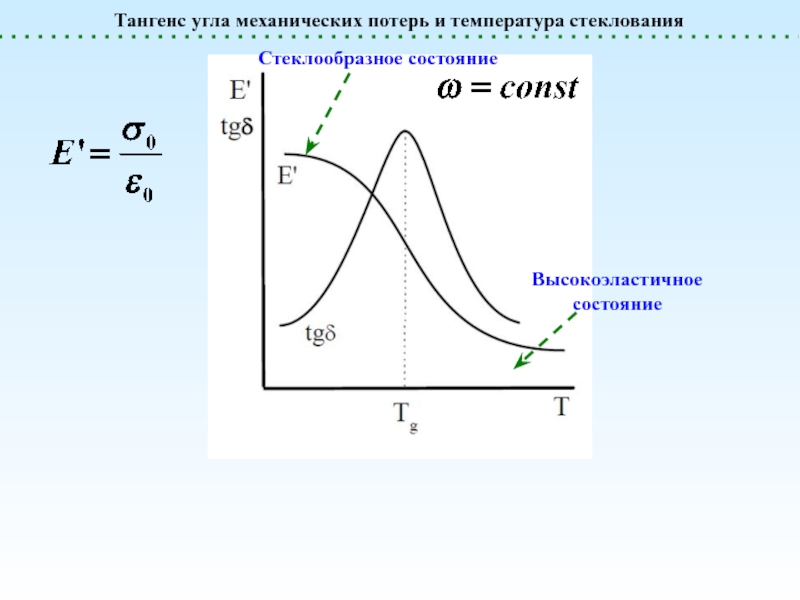
Температура стеклования (Тст) – это температура, при которой происходит размораживание молекулярной подвижности и переход от стеклообразного в вязкотекучее состояние. При Тст: kT = Ea

– начальная длина образца; l – длина деформированного образца; 

Идеальное твердое тело (упругие обратимые деформации)

Идеальная жидкость (деформация течения)

Закон Гука: Напряжение пропорционально деформации
Е – модуль Юнга. Показывает силу межмолекулярного взаимодействия

Закон Ньютона: Напряжение пропорционально скорости развития деформации
 – вязкость. Показывает силу трения между молекулами

= const, S0 = const)
напряжении ( = const)
и времени

Термомеханический анализ

Низкомолекулярное аморфное вещество

Низкомолекулярное кристаллическое вещество



Tст

(сегмент) < kT < Еа (клубок)
Высокоэластичное состояние
E – мало, 

Еа (клубок) < kT

Вязкотекучее состояние

Пластмассы или стекла

Эластомеры (каучуки)

Структурные особенности макромолекул.

Из-за гибкости полимерная цепь разделяется на СЕГМЕНТЫ – отрезки цепи, которые могут двигаться независимо друг от друга. Поэтому можно выделить две структурные единицы в макромолекуле – сегмент и саму макромолекулу. Понятно, что энергия активации перемещения сегмента меньше энергии активации перемещения макромолекулы в целом
Еа (сегмент) < Еа (клубок)

Центр масс макромолекулы

подвижность «заморожена»
молекулярная подвижность «разморожена»
Низкомолекулярные соединения
Полимеры

– уникальное свойство полимеров
Вязкотекучее
состояние
Тст < T < Ттек

Небольшие по величине упругие обратимые деформации, Е- велико

Большие по величине упругие обратимые деформации, Е- мало

Необратимые деформации (течение)

Тст

Ттек

Тст. – температура стеклования; Ттек - температура текучести

Тст(4) = Тст(5) =Тст(6)
Tст
Tст
Tтек
М1 < М2 < М3

Ттек(1) < Ттек(2) < Ттек (3) < Ттек (4) < Ттек (5) < Ттек (6)

Tтек(1)

Tтек(2)

Влияние молекулярной массы полимера на характер термомеханических кривых.

Мсегмент

критическая масса, начиная с которой появляется плато высокоэластичности, а температура

Кинетический сегмент – минимальный отрезок цепи , способный к поступательным перемещениям.

Кинетический сегмент – минимальный отрезок цепи, начиная с которого на термомеханических кривых появляется плато высокоэластичности, а температура стеклования перестаёт зависеть от длины цепи;

Кинетический сегмент учитывает гибкость макромолекулы при наличии межмолекулярного взаимодействия с соседними макромолекулами

М(кинетический сегмент) > М(сегмент Куна)

оС
Тст = + 110оС
Типичные каучуки (эластомеры) (Тст

Полиизобутилен

Цис-полибутадиен

Полидиметилсилоксан

Тст = -73оС

Тст = -106оС

Тст = -130оС

Тст. – важнейшая характеристика любого полимера, определяющая области его практического применения как материала

Практическое значение температуры стеклования

(поляризуемости цепи);
Увеличении свободного объёма (разрыхлении) материала;
Полиамид-3
Полиамид-6
Полиамид-11
Тст = +110 оС
Тст =

Тст = +42 оС

Полиметилметакрилат

Полиэтилметакрилат

Полибутилметакрилат

Тст = + 110оС

Тст = + 65оС

Тст = + 25оС

Влияние химической структуры полимеров на температуру стеклования.

Уменьшение доли полярных CO-NH- групп в цепи

Увеличение объёма боковых заместителей («рыхлости») цепи

целью понижения температуры стеклования полимера.
(При этом также понижается и

Полярные полимеры (например, поливиниловый спирт – пластификатор – вода)

H2O

Х – мольная доля пластификатора ;
k’ – константа

Пластификация полимеров.

Требование к пластификатору:
Хорошая смешиваемость с полимером (хорошее сродство к полимеру);
Низкая летучесть;
Малый коэффициент диффузии в полимере

T = T ст- Tст(пластификатор)

Механизм действия пластификатора – экранирование полярных взаимодействий в полимере

Правило мольных долей

Nп – число молей пластификатора; Nпл.зв. – число молей звеньев полимера

Неполярные полимеры (например, полистирол – пластификатор – диоктилфталат)

Механизм действия пластификатора – увеличение свободного объёма в полимере

Правило объёмных долей

 – объемная доля пластификатора ;
k’’ – константа

Vп – объём пластификатора; Vполим – объем полимера

объём, плотность, теплоёмкость и др. как функции температуры)
Т
Теплоёмкость
Тст
Vуд – удельный

В жидком состоянии теплоёмкость выше, чем в твёрдом;  при переходе через температуру стеклования теплоёмкость претерпевает скачок.

– температура термического разложения полимера; Мсш – масса отрезка цепи

Тст

Ттек

Редкая сшивка
Не влияет на Тст;
Предотвращает течение при Т > Ттек. (т.е. делает полимер нетекучим);
Предотвращает ползучесть (медленное течение) в области плато высокоэластичности при Тст < T < Ттек

за счет направленного поступательного движения отдельных сегментов в том же

EA – энергия активации вязкого течения (совпадает с энергией активации поступательного движения кинетических сегментов); не зависит от молекулярной массы полимера, зависит только от химической структуры мономерных звеньев.

предэкспотенциальный множитель. Зависит от молекулярной массы.
lg
lgMсrетка
lgM
Мс – молекулярная масса

полностью разрушена напряжением

 () при Т = const - основа анализа механических



Для низкомолекулярных упругих твердых тел:

Точка разрыва (разрушения) образца

пр

пр и пр - предел прочности - предельно достижимые деформация и напряжение в образце без его разрушения.
Е – тангенс угла наклона зависимости  ().

f - сила упругости; l – длина образца; V – объём образца, A – работа, затраченная на деформацию образца

Площадь под кривой () -  есть работа (энергия) затраченная на деформацию материала, отнесенная к единице объёма.

каучуков
dU – изменение внутренней энергии системы; dА – работа, совершенная

Первый закон термодинамики

Изменением объёма при деформации можно пренебречь.

В общем случае упругая сила имеет энергетическую (fu) и энтропийную (fs) составляющие, связанные с изменением внутренней энергии и энтропии материала при деформации

Для низкомолекулярных упругих твердых тел – упругость целиком энергетическая:

Наоборот, для газов упругость (давление) газа имеет целиком энтропийную природу:

f

– E ~ 105 МПА;
Кварц – E ~ 105 МПА;
Пластмассы

В упругости каучуков присутствуют обе составляющие, причем основной вклад в упругость вносит энтропийная составляющая fs.

Природа энтропийной составляющей каучуков

Энтропия макромолекулы

Расстояние между концами цепи

fs > 0

fs > 0

fs = 0

Любая деформация макромолекулярного клубка сопровождается снижением его энтропии.
При снятии нагрузки клубок принимает исходный размер, задаваемый максимумом энтропии.
Деформация макромолекулярного клубка ОБРАТИМА

Модуль упругости изолированного клубка

цепи 10-6 – 10-4 сек;
Время жизни флуктуационного узла – 10

Узлы флуктуационной сетки – непостоянные во времени небольшие квазикристаллические образования (из параллельно уложенных участков макромолекул) и зацеплений макромолекул - обуславливают существование энергетической составляющей модуля упругости каучуков fu.

от закона Гука (т.е. от прямолинейной зависимости  от )

текучести (предел вынужденной эластичности)
Еа (сегмент)  kT, но
Еа (сегмент) 

пр

пр

  пр – деформация обратима;
 > пр – деформация необратима;

< Т2 < Т3 < Т4 < Т5 < Т6

пр

в.э.

Температура хрупкости (Тхр) – температура, ниже которой не наблюдается явления вынужденной эластичности. Ниже температуры хрупкости полимер ведет себя как упругое хрупкое тело, т.е. зависимость  от  прямолинейна, а материал разрушается уже при небольших деформациях. На термомеханической кривой Тхр не проявляется.
При Т < Тхр: пр < в.э.

Т2 = Тхр

– разрушение полимера происходит ХРУПКО?
Большая площадь под кривой 

Тхр

T < Тхр

Малая площадь под кривой  -  . Только часть подведенной энергии уходит на деформацию . Остальной избыток – на образование новой поверхности  много осколков.

Из-за явления вынужденной эластичности полимеры при Тхр.< Т < Tст называют пластическими массами (пластиками).

неравновесного состояния в равновесное
x – степень отклонения параметра системы от

Время релаксации – время, за которое степень отклонения какого-либо параметра системы от равновесного уменьшится в е раз.

– образец мгновенно деформируют до заданной постоянной величины  =

Невулканизированные эластомеры

При t  0 –   o – обратимая деформация – каучук – упругое (гуковское тело); (клубки развернуты, флуктуацнонные узлы напряжены);
При t     0 – необратимая деформация (течение) - каучук – вязкая жидкость; (клубки свёрнуты, флуктуацнонные узлы ненапряжены)

Время релаксации уменьшается с ростом температуры

образцу прикладывают постоянное напряжение  = const. Т = const.

В момент времени t1 и t2 напряжение мгновенно сбрасывается до нуля. Получают кривые 2 и 3 релаксации деформации

Для предотвращения ползучести каучуки вулканизируют (сшивают).

Вязкоупругость (упруговязкость) – способность тела одновременно проявлять как свойства жидкости (течение), так и твердого тела (гуковская деформация). Полимеры – вязкоупругие тела.

эластомер
Диаграмма растяжение – сокращение 0max0 (|d/dt| = const). Цикл нагрузка

Гистерезис (от греческого hysteresis – отставание, опаздывание) – в данном случае неоднозначная зависимость величины деформации тела (физическая величина, характеризующая состояние тела) от напряжения (внешних условий). Петля гистерезиса – площадь между кривыми нагрузка - разгрузка. Наличие петли гистерезиса – свидетельство вязкоупругости деформируемого тела.

механических потерь – показывает, какая часть затраченной не деформацию работы

идеально упругого твердого тела нет отставания по фазе между напряжением

напряжения; ` - составляющая вектора напряжения, колеблющаяся в фазе с

E* - комплексный модуль; E` - модуль упругости или модуль накопления; E`` - модуль потерь; tg - тангенс угла механических потерь

стеклование – переход полимера из высокоэластического в стеклообразное состояние при

- время поступательного перемещания кинетической единицы (молекулы или сегмента), совпадает

Течение ледников – t  

Прыжки с высоты в воду t  0 – воды «твердеет»

сегмента сегм  D  . Увеличение частоты  приводит

Принцип температурно-временной суперпозиции (эквивалентности):для проявления полимером механических свойств понижение температуры эквивалентно повышению частоты воздействия, а повышение температуры эквивалентно понижению частоты воздействия.