Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Інтеграл та його застосування
Содержание
- 1. Інтеграл та його застосування
- 2. ФункціюF(x) називають первісною для функції f(x) на
- 3. Основна властивість первісної Якщо функція F(х) є
- 4. Невизначений інтегралСукупність усіх первісних для даної функції
- 5. Правила знаходження первісних
- 6. Таблиця первісних
- 7. Якщо функція f(х) визначена і непереривна на
- 8. Криволінійна трапеція - це фігура, обмежена графіком
- 9. Якщо на заданому відрізку [а;в] неперервні функції
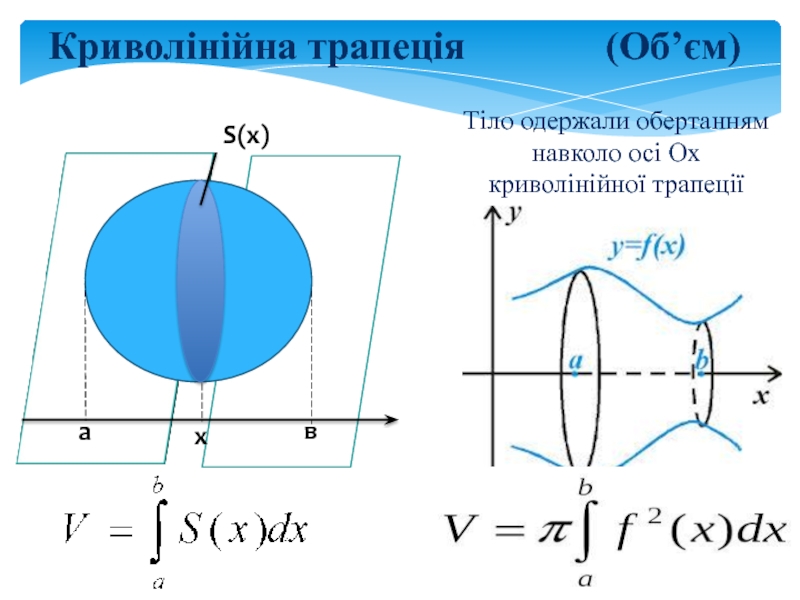
- 10. Криволінійна трапеція (Об’єм)Тіло одержали обертанням навколо осі Ох криволінійної трапеціїавхS(x)
- 11. Властивості визначених інтегралів1)2)3)4)5)
- 12. Обчислення визначеного інтегралу
- 13. 28y = (x – 2)20ABCD44
- 14. Розв’язанняS
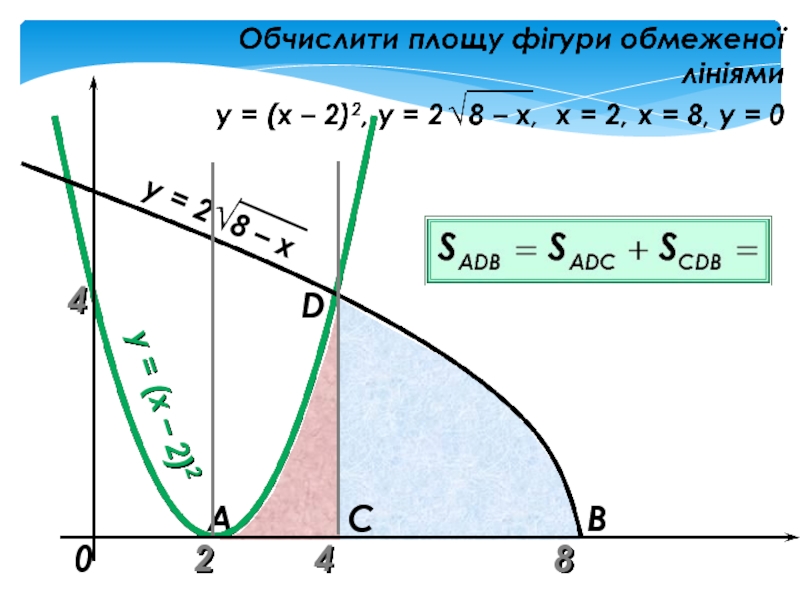
- 15. Обчислити площу фігури обмежену лініямита
- 16. Слайд 16
- 17. Слайд 17
- 18. Знайти похіднуСлайд 1F(x) = х3 +
- 19. Слайд 2Обчислити інтеграли1/28/3√2/2
- 20. Запишіть площу заштрихованої фігури як суму або
- 21. Тести:
- 22. 3. Знайдіть площу заштрихованной фігури.4. Обчисліть інтеграл:
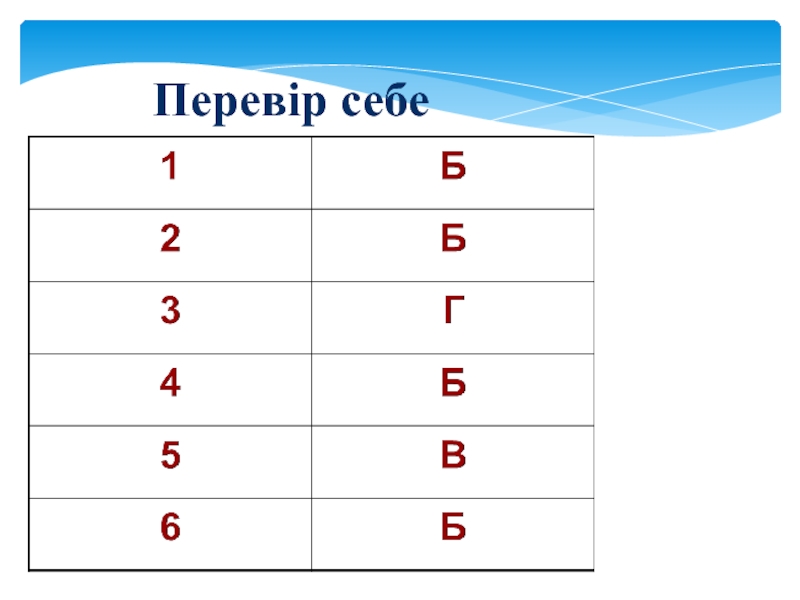
- 23. Перевір себе
- 24. Дякую за увагу!
- 25. Скачать презентанцию
ФункціюF(x) називають первісною для функції f(x) на даному проміжку, якщо для будь-якого х із цього проміжку F´(x)=f(x)
Слайды и текст этой презентации
Слайд 2ФункціюF(x) називають первісною для функції f(x) на даному проміжку, якщо
для будь-якого х із цього проміжку F´(x)=f(x)
Слайд 3Основна властивість первісної
Якщо функція F(х) є первісною для функції
f(х) на даному проміжку, а С-довільна стала, то функція F(х)+С
також є первісною для функції f(х), при цьому будь-яку первісну для функції f(х) можна записати у вигляді F(х)+С
Слайд 4Невизначений інтеграл
Сукупність усіх первісних для даної функції f(x) називають невизначеним
інтегралом і позначають символом
Тобто
=F(x)+C 
Слайд 7Якщо функція f(х) визначена і непереривна на відрізку [а; b]
і F(х)- її довільна первісна на цьому відрізку (F‘(x)=f(x))
, тоФормула Ньютона-Лейбніца
![Якщо функція f(х) визначена і непереривна на відрізку [а; b] і F(х)- її довільна первісна на цьому](/img/thumbs/083ed3b1cd58dc754131243eb8528b88-800x.jpg "Інтеграл та його застосування Якщо функція f(х) визначена і непереривна на відрізку [а; b] і")
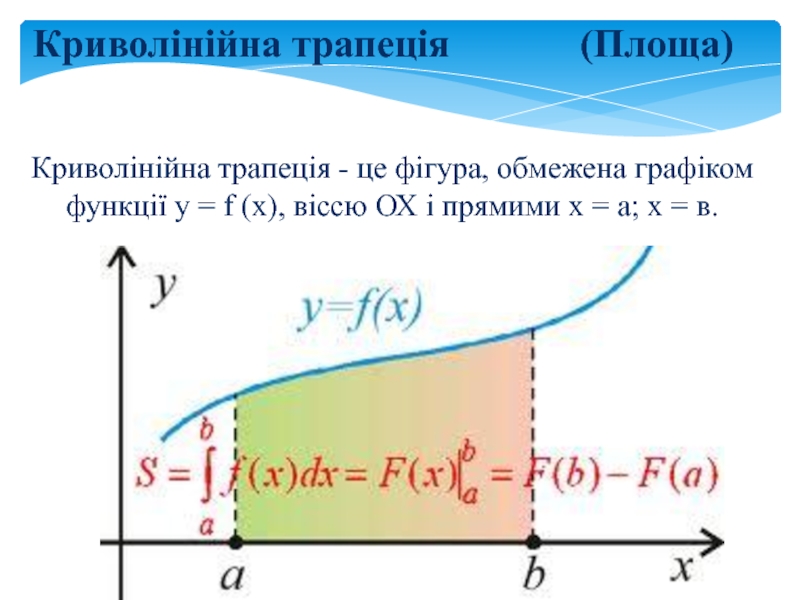
Слайд 8Криволінійна трапеція - це фігура, обмежена графіком функції y =
f (x), віссю ОХ і прямими х = а; х
= в.Криволінійна трапеція (Площа)
Слайд 9Якщо на заданому відрізку [а;в] неперервні функції y=f₁(x) і y=f₂(x)
мають таку властивість, що f₂(x)≥f₁(x) для всіх х є [а;в],
тоY=f₂(x)
Y=f₁(x)
![Якщо на заданому відрізку [а;в] неперервні функції y=f₁(x) і y=f₂(x) мають таку властивість, що f₂(x)≥f₁(x) для всіх](/img/thumbs/b57c2a327c0732ee43636504aabc18e2-800x.jpg "Інтеграл та його застосування Якщо на заданому відрізку [а;в] неперервні функції y=f₁(x) і y=f₂(x) мають")
Слайд 10Криволінійна трапеція (Об’єм)
Тіло одержали
обертанням навколо осі Ох криволінійної трапеції
а
в
х
S(x)
Слайд 18
Знайти похідну
Слайд 1
F(x) = х3 + х2 + С
F(x) =
2х + С
F(x) = -3 cosx + С
F(x) = 1/5(х
– 2) 5 + СF(x) = ⅓ sin3х+ С
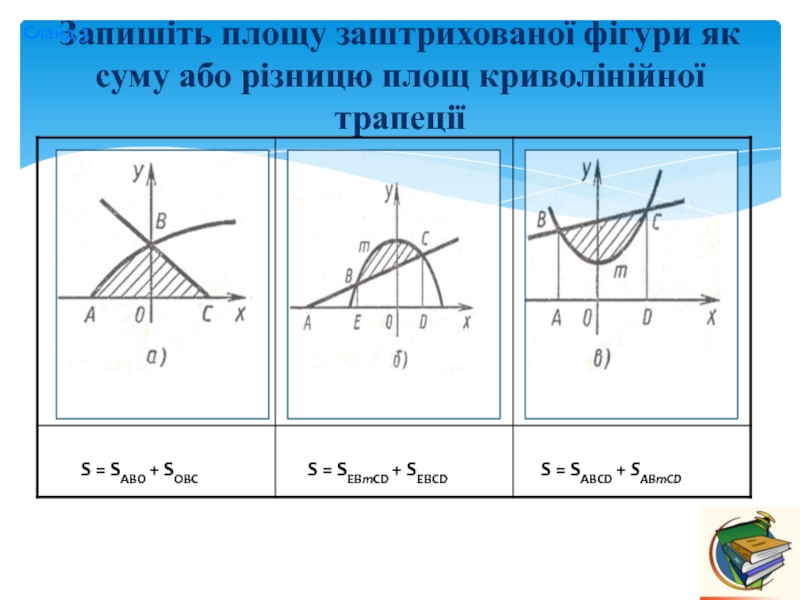
Слайд 20Запишіть площу заштрихованої фігури як суму або різницю площ криволінійної
трапеції
Слайд 3
S = SABO + SOBC
S = SEBmCD +
SEBCDS = SABCD + SABmCD
