Разделы презентаций

ОБРАБОТКА ЦИФРОВЫХ ИЗОБРАЖЕНИЙ: ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ

Содержание

Шеповалов А.О. Курсовой проект 2011Изучить основы компьютерной графики.Освоить функции ядра КТС Mathematica для обработки изображений.Изучить основы геометрических преобразований и дать характеристику указанных методов, реализованных в КТС Mathematica.Реализовать на любом языке программирования

Слайды и текст этой презентации

Слайд 1Шеповалов А.О. Курсовой проект 2011
ОБРАБОТКА ЦИФРОВЫХ ИЗОБРАЖЕНИЙ: ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ

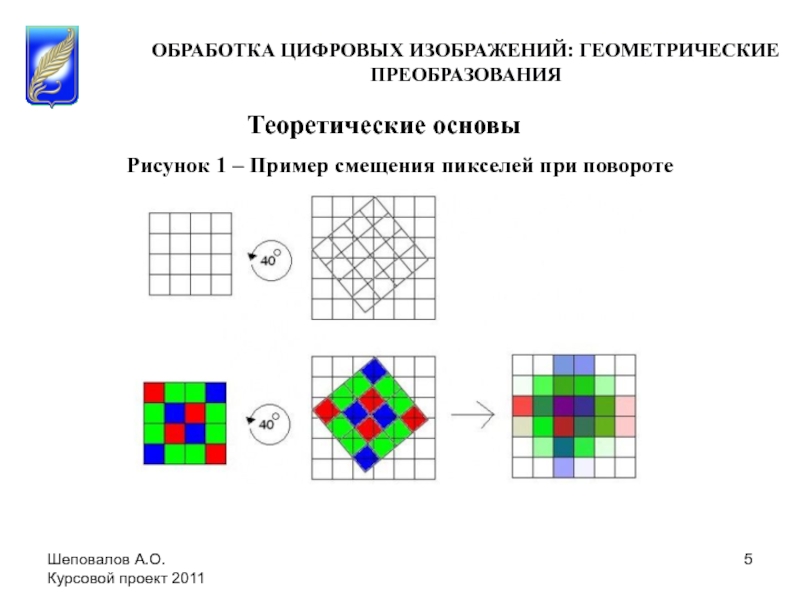
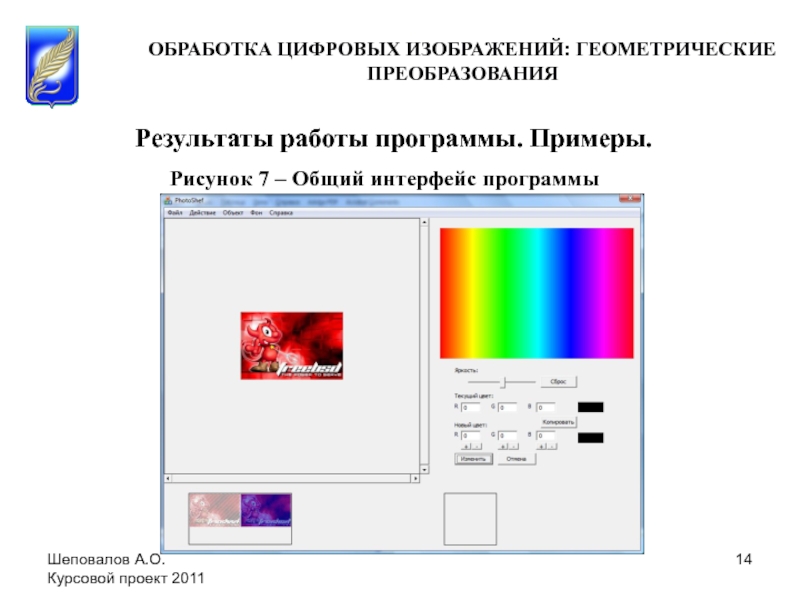
Шеповалов Артём Олегович
БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
Руководитель проекта
Кулинкович Виктория

Александровна
ассистент кафедры КТС

Кафедра компьютерных технологий и систем


Кафедра технологий программирования

Факультет Прикладной Математики и Информатики

Шеповалов А.О. Курсовой проект 2011ОБРАБОТКА ЦИФРОВЫХ ИЗОБРАЖЕНИЙ: ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ Шеповалов Артём ОлеговичБЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ

Слайд 2Шеповалов А.О. Курсовой проект 2011

Изучить основы компьютерной графики.
Освоить функции ядра

КТС Mathematica для обработки изображений.
Изучить основы геометрических преобразований и дать

характеристику указанных методов, реализованных в КТС Mathematica.
Реализовать на любом языке программирования некоторые из рассмотренных методов (согласовать с преподавателем).
Освоить приемы подготовки скриншотов и включения их в отчеты doc, компьютерные презентации ppt.


Перечень вопросов подлежащих разработке,
краткое содержание работы

ОБРАБОТКА ЦИФРОВЫХ ИЗОБРАЖЕНИЙ: ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ

Шеповалов А.О. Курсовой проект 2011Изучить основы компьютерной графики.Освоить функции ядра КТС Mathematica для обработки изображений.Изучить основы геометрических

Слайд 3Шеповалов А.О. Курсовой проект 2011
Теоретические основы
Представим, что изображение -

это матрица пикселей. Тогда при вращении изображения происходит наложение исходной

матрицы и повернутой на заданный угол. А поскольку единичный пиксель может быть только одного определенного цвета, то необходимо правильно распределить эти самые цвета.

ОБРАБОТКА ЦИФРОВЫХ ИЗОБРАЖЕНИЙ: ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ

Шеповалов А.О. Курсовой проект 2011Теоретические основы Представим, что изображение - это матрица пикселей. Тогда при вращении изображения

Слайд 4Шеповалов А.О. Курсовой проект 2011
Представим графическую интерпретацию. На левом рисунке

представлено исходное изображение. На среднем рисунке видно, как происходит пересечение

матриц исходного и повернутого изображений. Справа виден конечный результат работы алгоритма - происходит пропорциональное распределение цветов по ячейкам пиксельной матрицы.







Теоретические основы


ОБРАБОТКА ЦИФРОВЫХ ИЗОБРАЖЕНИЙ: ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ

Шеповалов А.О. Курсовой проект 2011 Представим графическую интерпретацию. На левом рисунке представлено исходное изображение. На среднем рисунке видно,

Слайд 5Шеповалов А.О. Курсовой проект 2011

ОБРАБОТКА ЦИФРОВЫХ ИЗОБРАЖЕНИЙ: ГЕОМЕТРИЧЕСКИЕ

ПРЕОБРАЗОВАНИЯ
Рисунок 1 – Пример смещения пикселей при повороте
Теоретические основы

Шеповалов А.О. Курсовой проект 2011 ОБРАБОТКА ЦИФРОВЫХ ИЗОБРАЖЕНИЙ: ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ Рисунок 1 – Пример смещения пикселей

Слайд 6Шеповалов А.О. Курсовой проект 2011
Пусть:
O - это центр поворота,


M - некая точка исходного изображения.
Для каждой точки

M нужно найти угол alpha между отрезком OM и горизонталью и длину r отрезка OM.








Теоретические основы


Алгоритмы поворота изображения

ОБРАБОТКА ЦИФРОВЫХ ИЗОБРАЖЕНИЙ: ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ

Рисунок 2 – Точка М исходного изображения

Шеповалов А.О. Курсовой проект 2011Пусть: O - это центр поворота, M - некая точка исходного изображения. Для

Слайд 7Шеповалов А.О. Курсовой проект 2011
Теперь, чтобы повернуть изображение на угол

beta, нужно каждой точке M присвоить цвет точки исходного изображения

с координатами x,y, где
x = xo + r * cos(alpha + beta)
y = yo + r * sin(alpha + beta)
xo,yo - центр поворота, r - длина отрезка OM











Теоретические основы


Алгоритмы поворота изображения

ОБРАБОТКА ЦИФРОВЫХ ИЗОБРАЖЕНИЙ: ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ

Шеповалов А.О. Курсовой проект 2011 Теперь, чтобы повернуть изображение на угол beta, нужно каждой точке M присвоить цвет

Слайд 8Шеповалов А.О. Курсовой проект 2011

Алгоритмы поворота изображения
ОБРАБОТКА ЦИФРОВЫХ

ИЗОБРАЖЕНИЙ: ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ
Рисунок 3 – Образ точки M при повороте

на угол beta

Теоретические основы

Шеповалов А.О. Курсовой проект 2011 Алгоритмы поворота изображенияОБРАБОТКА ЦИФРОВЫХ ИЗОБРАЖЕНИЙ: ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ Рисунок 3 – Образ

Слайд 9Шеповалов А.О. Курсовой проект 2011

Алгоритмы поворота изображения
Важно

именно каждой точке нового изображения сопоставлять точку старого изображения, а

не наоборот, так как иначе некоторые точки нового изображения останутся не закрашенными.




















ОБРАБОТКА ЦИФРОВЫХ ИЗОБРАЖЕНИЙ: ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ

Теоретические основы

Шеповалов А.О. Курсовой проект 2011 Алгоритмы поворота изображения Важно именно каждой точке нового изображения сопоставлять точку

Слайд 10Шеповалов А.О. Курсовой проект 2011

Алгоритмы поворота изображения
При использовании

декартовой системы координат используется следующий алгоритм поворота.
В двумерном пространстве поворот

можно описать одним углом со следующей матрицей линейного преобразования в декартовой системе координат:


Положительным углам при этом соответствует вращение вектора против часовой стрелки в обычной, правосторонней системе координат, и по часовой в левосторонней системе координат.


















ОБРАБОТКА ЦИФРОВЫХ ИЗОБРАЖЕНИЙ: ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ

Теоретические основы

Шеповалов А.О. Курсовой проект 2011 Алгоритмы поворота изображения При использовании декартовой системы координат используется следующий алгоритм поворота. В

Слайд 11Шеповалов А.О. Курсовой проект 2011
Результаты работы программы. Примеры.

Рассмотрим пример работы

функции поворота на следующем изображении:
Рисунок 4 – Исходное изображение
ОБРАБОТКА ЦИФРОВЫХ

ИЗОБРАЖЕНИЙ: ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ
Шеповалов А.О. Курсовой проект 2011Результаты работы программы. Примеры. Рассмотрим пример работы функции поворота на следующем изображении:Рисунок 4 –

Слайд 12Шеповалов А.О. Курсовой проект 2011
Рисунок 5 – Файл->Открыть
Сначала откроем изображение,

выбрав Файл->Открыть:

ОБРАБОТКА ЦИФРОВЫХ ИЗОБРАЖЕНИЙ: ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ
Результаты работы программы. Примеры.

Шеповалов А.О. Курсовой проект 2011Рисунок 5 – Файл->Открыть Сначала откроем изображение, выбрав Файл->Открыть: ОБРАБОТКА ЦИФРОВЫХ ИЗОБРАЖЕНИЙ: ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ Результаты

Слайд 13Шеповалов А.О. Курсовой проект 2011



Укажем местоположение файла:
ОБРАБОТКА ЦИФРОВЫХ ИЗОБРАЖЕНИЙ: ГЕОМЕТРИЧЕСКИЕ

ПРЕОБРАЗОВАНИЯ
Результаты работы программы. Примеры.
Рисунок 6 – Указание места размещения файла

Шеповалов А.О. Курсовой проект 2011 Укажем местоположение файла:ОБРАБОТКА ЦИФРОВЫХ ИЗОБРАЖЕНИЙ: ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ Результаты работы программы. Примеры.Рисунок 6 –

Слайд 14Шеповалов А.О. Курсовой проект 2011


ОБРАБОТКА ЦИФРОВЫХ ИЗОБРАЖЕНИЙ: ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ
Результаты работы

программы. Примеры.
Рисунок 7 – Общий интерфейс программы

Шеповалов А.О. Курсовой проект 2011 ОБРАБОТКА ЦИФРОВЫХ ИЗОБРАЖЕНИЙ: ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ Результаты работы программы. Примеры.Рисунок 7 – Общий интерфейс

Слайд 15Шеповалов А.О. Курсовой проект 2011



Далее необходимо выполнить следующие команды: Действие->Поворот.
ОБРАБОТКА

ЦИФРОВЫХ ИЗОБРАЖЕНИЙ: ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ
Результаты работы программы. Примеры.
Рисунок 8 – Действие->Поворот

Шеповалов А.О. Курсовой проект 2011 Далее необходимо выполнить следующие команды: Действие->Поворот.ОБРАБОТКА ЦИФРОВЫХ ИЗОБРАЖЕНИЙ: ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ Результаты работы программы.

Слайд 16Шеповалов А.О. Курсовой проект 2011


ОБРАБОТКА ЦИФРОВЫХ ИЗОБРАЖЕНИЙ: ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ
Результаты работы

программы. Примеры.
В появившемся диалоговом меню необходимо ввести требуемый угол поворота

в градусах против часовой стрелки и нажать OK:

Рисунок 9 – Диалоговое окно, запрашивающее величину угла поворота

Шеповалов А.О. Курсовой проект 2011 ОБРАБОТКА ЦИФРОВЫХ ИЗОБРАЖЕНИЙ: ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ Результаты работы программы. Примеры. В появившемся диалоговом меню необходимо

Слайд 17Шеповалов А.О. Курсовой проект 2011


ОБРАБОТКА ЦИФРОВЫХ ИЗОБРАЖЕНИЙ: ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ
Результаты работы

программы. Примеры.
Программа выполнит поворот изображения и выдаст его на рабочий

экран:

Рисунок 10 – Итоговое изображение

Шеповалов А.О. Курсовой проект 2011 ОБРАБОТКА ЦИФРОВЫХ ИЗОБРАЖЕНИЙ: ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ Результаты работы программы. Примеры. Программа выполнит поворот изображения и

Слайд 18Шеповалов А.О. Курсовой проект 2011

ОБРАБОТКА ЦИФРОВЫХ ИЗОБРАЖЕНИЙ: ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ
Результаты работы

программы. Примеры.
Для сохранения изображения нужно выполнить последовательность команд Файл->Сохранить или

Файл->Сохранить как. В первом случае файл с исходным изображением будет обновлён новым, а во втором будет создан новый отдельный файл с заданным именем:

Рисунок 11 – Файл->Сохранить как

Шеповалов А.О. Курсовой проект 2011 ОБРАБОТКА ЦИФРОВЫХ ИЗОБРАЖЕНИЙ: ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ Результаты работы программы. Примеры. Для сохранения изображения нужно выполнить

Слайд 19Шеповалов А.О. Курсовой проект 2011

Изучены основы компьютерной графики.
Освоены функции ядра

КТС Mathematica для обработки изображений.
Изучены основы геометрических преобразований и дана

характеристика указанных методов, реализованных в КТС Mathematica.
Реализована на языке программирования C++ функция поворота изображения.
Освоены приемы подготовки скриншотов и включения их в отчеты doc, компьютерные пре-зентации ppt.

Заключение

ОБРАБОТКА ЦИФРОВЫХ ИЗОБРАЖЕНИЙ: ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ

Шеповалов А.О. Курсовой проект 2011Изучены основы компьютерной графики.Освоены функции ядра КТС Mathematica для обработки изображений.Изучены основы геометрических

Похожие презентации

Наш проект 5 –А клас c Запорожской частной школы РЕАЛ Апрель 2014 Наш проект 5 –А клас c Запорожской частной школы РЕАЛ Апрель 2014 "Я-житель 192
RIGHTS OF PERSONS WITH DISABILITIES ACT, 201 6 RIGHTS OF PERSONS WITH DISABILITIES ACT, 201 6 178
История создания и развития Вооруженных сил России История создания и развития Вооруженных сил России 207
ДЕЙСТВИЯ С ДРОБЯМИ ДЕЙСТВИЯ С ДРОБЯМИ 159
Дорога и безопасность Дорога и безопасность 350
Лекция 3 Лекция 3 214
Федеральное государственное бюджетное образовательное учреждение высшего Федеральное государственное бюджетное образовательное учреждение высшего 176
introductory_lesson introductory_lesson 214
комплекс упражнений для ускорения комплекс упражнений для ускорения 206
Планировочные районы и транспортная инфраструктура Севастополя Планировочные районы и транспортная инфраструктура Севастополя 158
Техника прыжка в высоту способом Техника прыжка в высоту способом "перешагивание" 264
Повторение по теме «Диалог» Повторение по теме «Диалог» 670
Тренинг по разбору заданий ГИА в соответствии со спецификацией и кодификатором Тренинг по разбору заданий ГИА в соответствии со спецификацией и кодификатором 312
Тақырып: ОЖЖ-дегі тежелу механизмдері. ОЖЖ-дегі тежелудің координациялық Тақырып: ОЖЖ-дегі тежелу механизмдері. ОЖЖ-дегі тежелудің координациялық 615
6-дәріс Инфекция туралы ілім. Инфекциялық процестің сипаты. Бактериялардын 6-дәріс Инфекция туралы ілім. Инфекциялық процестің сипаты. Бактериялардын 1250
Крокодилы: свирепые и коварные Крокодилы: свирепые и коварные 303
ТЕМА 4 Критерии качества перевода ТЕМА 4 Критерии качества перевода 284
Социальные нормы и отклоняющееся поведение Социальные нормы и отклоняющееся поведение 261
ФОРМИРОВАНИЕ ТЕЛЕВИДЕНИЯ ФОРМИРОВАНИЕ ТЕЛЕВИДЕНИЯ 241
Бюджет города на 2020 год и плановый период 2021 – 2022 годов Бюджет города на 2020 год и плановый период 2021 – 2022 годов 220

Обратная связь

Если не удалось найти и скачать доклад-презентацию, Вы можете заказать его на нашем сайте. Мы постараемся найти нужный Вам материал и отправим по электронной почте. Не стесняйтесь обращаться к нам, если у вас возникли вопросы или пожелания:

Email: Нажмите что бы посмотреть 

Что такое TheSlide.ru?

Это сайт презентации, докладов, проектов в PowerPoint. Здесь удобно  хранить и делиться своими презентациями с другими пользователями.

Для правообладателей

Яндекс.Метрика