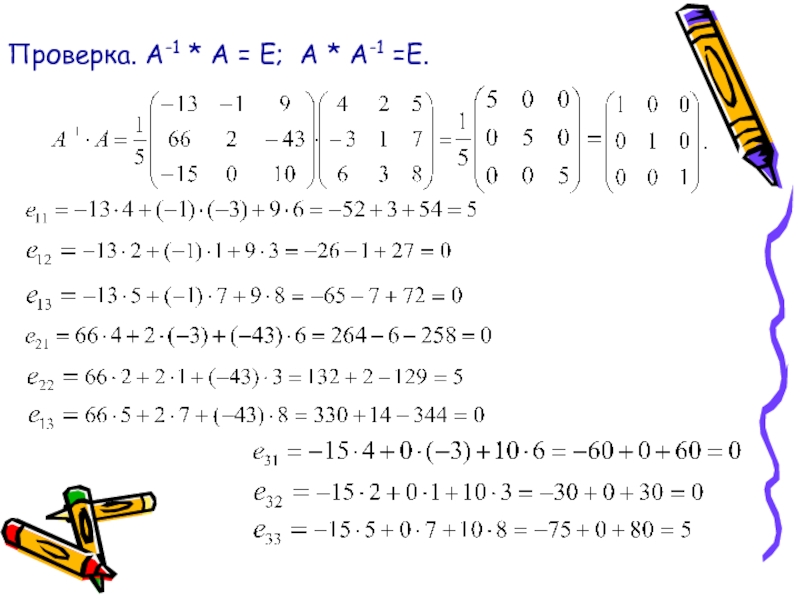Обратная матрица, решение СЛАУ матричным методом. Совместность СЛАУ

матрице А, если выполняется условие: А * A-1

= A-1 * A = E , где Е – единичная матрица.

Теорема (об обратной матрице).
Если определитель detA квадратной матрицы A (n x n) не равен нулю, то у неё существует обратная матрица A-1, вычисляемая по формуле:

(3)


где алгебраическое дополнение к элементу аij матрицы А.

обратной матрицы.
Найдем произведение матриц А * А-1 , при detA

верно
Аналогично проверяется А-1 * А = Е.

существования А-1. Имеем: det(A*A-1) =

detA * detA-1 ; det E = detA * detA-1 ; det E = 1. При detA=0 получим 1=0, что неверно. Значит, detA . Доказано.

Замечание.
Квадратная матрица, определитель которой равен нулю, называется вырожденной. Если определитель матрицы не равен нулю, то её называют невырожденной.

Гаусса, аналогичным методу Гаусса для расширенных матриц СЛАУ.
Схема:

Решение СЛАУ матричным методом.
Задана СЛАУ АХ=В. Найти Х.
Пусть A-невырожденная матрица, тогда существует А-1. Имеем: А-1АХ= А-1В; EX=А-1В;
X= А-1В - матричное решение СЛАУ

матрицы А( m x n) называется определитель, образованный элементами матрицы,

стоящими на пересечении любых k строк и k столбцов.
2) Рангом r матрицы А называется наибольший порядок её минора, не равного нулю.
Обозначение: r=r(A) – ранг матрицы А.
3) Всякий отличный от нуля минор r-го порядка называют базисным минором, также строки и столбцы, образующие этот минор – базисными.
Пример.

столбцов или строк;
2) умножение столбца (строки) на число,

отличное от нуля;
3) прибавление к столбцу (строке) другого столбца (другой строки), умноженного предварительно на некоторое число;
4) зачеркивание нулевого столбца (строки);
5) транспонирование.
Пример. Найти ранг матрицы А.

решение; если СЛАУ не имеет решений, то она называется несовместной.
Теорема

Кронекера - Капелли.
СЛАУ вида

(4)


совместна тогда и только тогда, когда ранг её матрицы А равен рангу расширенной
матрицы:

(без доказательства).