Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Общая схема исследования функции и построения графика
Содержание
- 1. Общая схема исследования функции и построения графика
- 2. Исследование функции y= f(x) целесообразно вести в определенной последовательности:
- 3. Найти область определения функцииНайти (если это можно)
- 4. Найти асимптоты графика функцииНайти интервалы монотонности функцииНайти экстремумы функцииНайти интервалы выпуклости и точки перегиба графика функции
- 5. ПримерНеобходимо исследовать эту функцию и построить ее графикДана функция
- 6. Решение1. Найти область определения функцииФункция не определена
- 7. 2. Найти (если это можно) точки пересечения
- 8. 3. Найти интервалы знакопостоянства функции (промежутки,
- 9. 4. Выяснить, является ли функция
- 10. 5. Найти асимптоты графика функции Прямые
- 11. 6. Найти интервалы монотонности функции Находим
- 12. 7. Найти экстремумы функции Находим интервалы
- 13. 8. Найти интервалы выпуклости и точки перегиба
- 14. Вторая производная равна нулю или
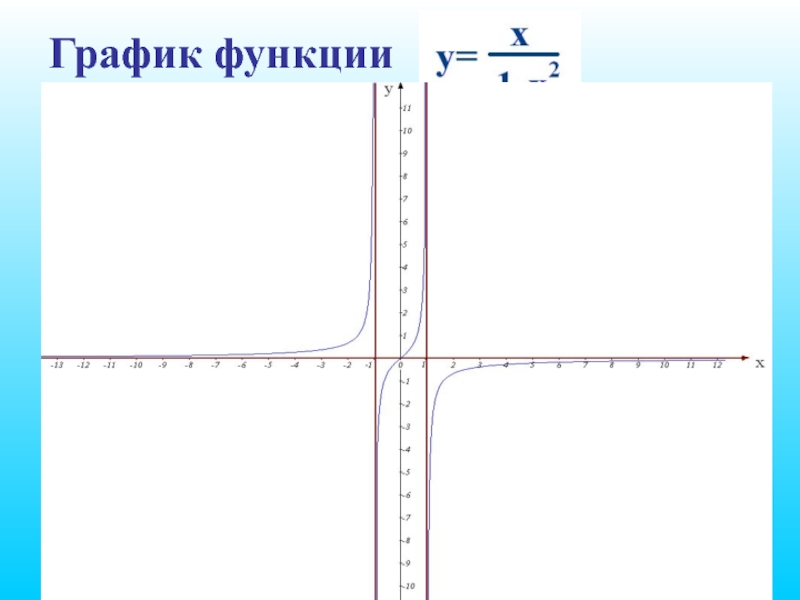
- 15. График функции
- 16. Скачать презентанцию
Исследование функции y= f(x) целесообразно вести в определенной последовательности:
Слайды и текст этой презентации
Слайд 3Найти область определения функции
Найти (если это можно) точки пересечения графика
с осями координат
Найти интервалы знакопостоянства функции (промежутки, на которых f(x)>0
или f(x)<0)Выяснить, является ли функция четной, нечетной или общего вида
Слайд 4Найти асимптоты графика функции
Найти интервалы монотонности функции
Найти экстремумы функции
Найти интервалы
выпуклости и точки перегиба графика функции
Слайд 6Решение
1. Найти область определения функции
Функция не определена при x =
1 и x = -1. Область ее определения состоит из
трех интервалов (-∞; -1), (-1; 1), (1; +∞), а график из трех ветвей.
Слайд 72. Найти (если это можно) точки пересечения графика функции
с осями координат
Если x = 0,
то y = 0. График пересекает ось Oy в точке O(0;0). Если y = 0, то x = 0. График пересекает ось Ox в точке O(0;0).
Слайд 83. Найти интервалы знакопостоянства функции (промежутки, на которых f(x)>0 или
f(x)0) на интервалах (-∞; -1) и
(0; 1).Функция знакоотрицательна (y<0) на интервалах (-1; 0) и (1; +∞).
Слайд 94. Выяснить, является ли функция
четной, нечетной или общего вида
Функция является нечетной, т.к.
Следовательно, график ее симметричен относительно начала координат. Для построения графика достаточно исследовать ее при x ≥ 0
Слайд 105. Найти асимптоты графика функции
Прямые x = 1
и x = -1 являются ее вертикальными асимптотами.
Прямая
у = 0 является ее горизонтальной асимптотой.
Слайд 116. Найти интервалы монотонности функции
Находим интервалы возрастания и
убывания функции. Т.к.
,то > 0 в области определения, и функция является возрастающей на каждом интервале области определения.
Слайд 127. Найти экстремумы функции
Находим интервалы возрастания и убывания
функции. Т.к.
,то критическими точками являются точки x1 = 1 и x2 = -1 ( не существует), но они не принадлежат области определения функции. Функция экстремумов не имеет.
Слайд 138. Найти интервалы выпуклости и точки перегиба графика функции
Исследуем функцию на выпуклость. Находим :
Слайд 14 Вторая производная равна нулю или не существует в
точках x1 = 0, x2 = -1 и x3 =
1.Точка О(0; 0) – точка перегиба графика функции.
График выпуклый вверх на интервалах (-1; 0) и (1; +∞); выпуклый вниз на интервалах (-∞; -1) и (0; 1).
