Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Общие свойства линейных дискриминантных функций в детерминистской постановке
Содержание
- 1. Общие свойства линейных дискриминантных функций в детерминистской постановке
- 2. Общие свойства линейных дискриминантных функций в детерминистской
- 3. Находим некоторую решающую функцию d(X), которая удовлетворяет
- 4. Оказывается, что не все возможные классификации могут
- 5. ПримерРасчет количества возможных линейных дихотомий для N
- 6. Мы можем построить некие функции от x,
- 7. Как ведет себя данная функция?Определим параметр λ:
- 8. При λ < 2 вероятность близка к
- 9. Персептронный алгоритм получения линейных решающих правил
- 10. Персептронный алгоритм получения линейных решающих правил Простейший
- 11. Тогда наша система неравенств сводится к более
- 12. 2.
- 13. Показано, что если решение существует, то алгоритм
- 14. Скачать презентанцию
Общие свойства линейных дискриминантных функций в детерминистской постановкеЗдесь рассматривается задача классификации данных, заданных в виде конечных наборов многомерных векторов.Данный подход основан на нахождении линейных дискриминантных функций:d( ) = T
Слайды и текст этой презентации
Слайд 1ОБУЧАЕМЫЕ КЛАССИФИКАТОРЫ. ДЕТЕРМИНИСТСКИЙ ПОДХОД
Общие свойства линейных дискриминантных функций в
детерминистской постановке
Слайд 2Общие свойства линейных дискриминантных функций в детерминистской постановке
Здесь рассматривается задача
классификации данных, заданных в виде конечных наборов многомерных векторов.
Данный подход
основан на нахождении линейных дискриминантных функций:d( ) = T + WN+1 > 0 (или ≤)
Мы имеем следующее:
∈ X1 X1 = {X i }
∈ X2 X2 = {X j }
Общий объем выборки: N = N1 + N2
Задача заключается в нахождении решающей функции, которая удовлетворяет N линейным неравенствам, при условии N > n:
Слайд 3Находим некоторую решающую функцию d(X), которая удовлетворяет неравенствам (*) и
задает некоторую дихотомию, то есть разделение исходного пространства на два
полупространства. Возникает вопрос можно ли решить данную систему неравенств. Возникает понятие разделяющей мощности решающего правила – это число возможных способов классификации данного объекта, которые допускаются с данной функцией.Можно рассмотреть количество линейных возможных дихотомий для N точек в линейном пространстве n. При этом каждая линейная решающая функция задает две дихотомии (так как нумерация классов может быть 1-2 или наоборот 2-1)
Стоит задача разбиения точек в n-мерном пространстве с помощью (n-1) - мерной гиперплоскости.
Общее возможных дихотомий для N точек равно 2N – это все
возможные классификации: 2N =
Слайд 4Оказывается, что не все возможные классификации могут быть заданы линейно.
На рисунке представлены 4 точки , которые могут быть разделены
с помощью 7 гиперплоскостей ( в двумерном пространстве – просто линиями)Однако существуют дихотомии, которые не могут быть реализованы линейно
∙ x2 Линейно не могут быть заданы:
I класс (x2, x4)
x1 ∙ ∙ x3 II класс (x1, x3)
∙ x4
N = 4 Q = 24 = 16 QP = 16 – 2 = 14
Формула, которая задает возможное количество классификаций (дихотомий), реализуемых линейно для N объектов, размерность пространства n:
Эта формула имеет место только тогда, когда точки объекта расположено “хорошо”. Это означает, что ни одна из точек группы, состоящей из (n+1) точки, не лежит в подпространстве размерности (n-1).
Слайд 5Пример
Расчет количества возможных линейных дихотомий для N точек в n-мерном
пространстве:
С ростом размерности число возможных дихотомий резко возрастает.
Рассмотрим использование
обобщенных линейных дискриминантных функций, полученных с помощью нелинейного преобразования исходного n-мерного пространства в пространство размерности k>nd(X) = f1(x)W1 + f2(x)W2 + ... + fk(x)Wk + Wk+1 , где k > n
Слайд 6Мы можем построить некие функции от x, путем некоего нелинейного
преобразования и соответственно мы можем повысить размерность пространства и искать
решение уже там.Можно ввести понятие вероятность получения линейной дихотомии – это функция PN,K – вероятность того, что данная дихотомия будет реализована с помощью линейной функции.
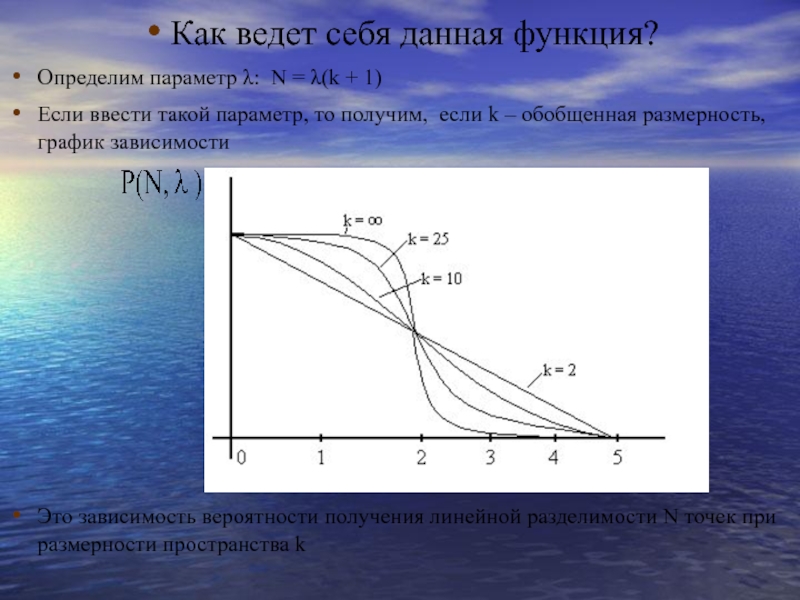
Слайд 7Как ведет себя данная функция?
Определим параметр λ: N = λ(k
+ 1)
Если ввести такой параметр, то получим, если k –
обобщенная размерность, график зависимости Это зависимость вероятности получения линейной разделимости N точек при размерности пространства k
Слайд 8При λ < 2 вероятность близка к единице.
При N
2(k + 1) вероятность достаточно близка к единице.
Величина Ck
= 2(k+1) называется мощностью соответствующая линейной решающей функции.Чем больше размерность, тем больше мощность решающей функции.
Можно показать, что для исходного пространства с размерностью dim X = n мощность Ck для обобщенных линейных решающих функций определяется следующим образом:
гиперплоскость – Ck =2(n+1);
гиперсфера – Ck = 2(n+2);
поверхность второго порядка: Ck =(n+1)(n+2)
полиномиальная поверхность порядка r: Ck =2Crn+r
Слайд 10Персептронный алгоритм получения линейных решающих правил
Простейший методы получения линейных
решающих функций на основе персептронных алгоритма обучения основывается на рекуррентном
построении решающего правила путем коррекции ошибок.Требуется найти , Wn+1 для построения решающего правила
на основе использования конечных обучающих выборок.
Введем понятие расширенных векторов . Перейдем от размерности n к n+1 следующим образом:
Слайд 11Тогда наша система неравенств сводится к более простой задаче:
(или <) x ∈ X1 (x ∈ X2)
Персептронный алгоритм основан на последовательном просмотре обучающей выборки:
X1, ... XN1 ………. XN
X1 X2
N = N1 + N2
Процесс обучения заключается в том, что мы циклически просматриваем выборку и подставляем получаемое значение в W в (*), и на каждом шаге просмотра производим или не производим коррекцию весового вектора.
1. , если
В этом случае получен правильный ответ при классификации текущего вектора
Слайд 122.
, если
, если
Этот случай соответствует ошибочной классификации и соответственно производится коррекция весового вектора (должно быть С>0)
Эта процедура и является процедурой обучения персептронного типа.
Пусть мы имеем величину весового вектора после коррекции:
Подставим новый весовой вектор в выражение для решающей функции:
Видно, что значение весовой функции увеличилось на положительную
величину , то есть мы продвинулись к правильному решению.
Слайд 13Показано, что если решение существует, то алгоритм сходится за конечное
число шагов.
Различные варианты выбора коэффициента C позволяют улучшить данный алгоритм:
1.
С – константа . Скорость сходимости может быть мала.2. С = Cn = var(n)
Попробуем менять C на каждом шагу так .чтобы сразу получить на текущем векторе правильное решение. Здесь можно использовать такой выбор
, отсюда следует
Вывод:
Рассмотренный алгоритм появился на основе интуитивных соображений при разработке моделей работы головного мозга человека при решении задач обучения.