Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
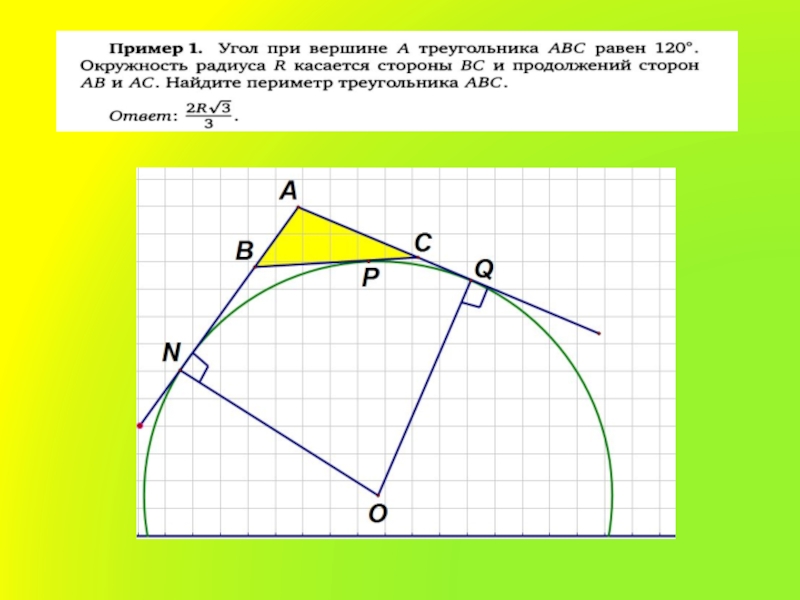
Окружность. Хорды, касательные, секущие. Углы между хордами, секущими,
Содержание
- 1. Окружность. Хорды, касательные, секущие. Углы между хордами, секущими,
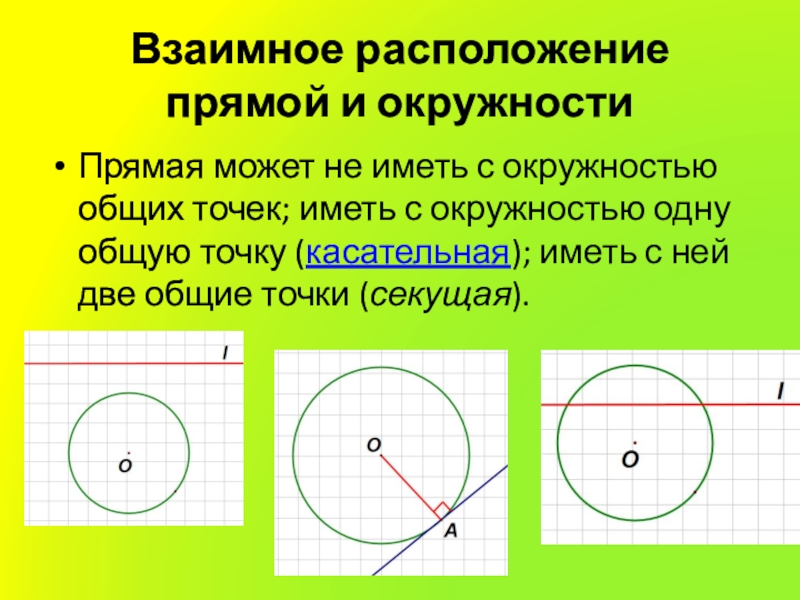
- 2. Взаимное расположение прямой и окружностиПрямая может не
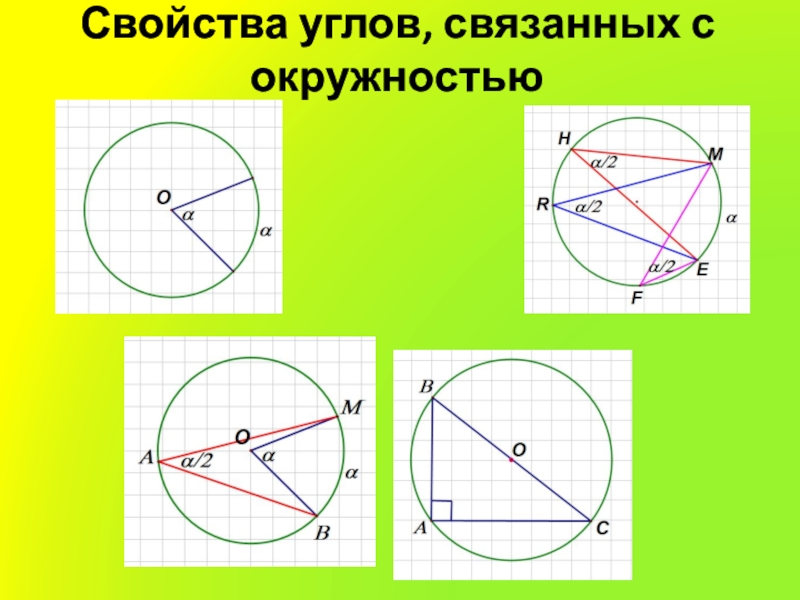
- 3. Свойства углов, связанных с окружностью
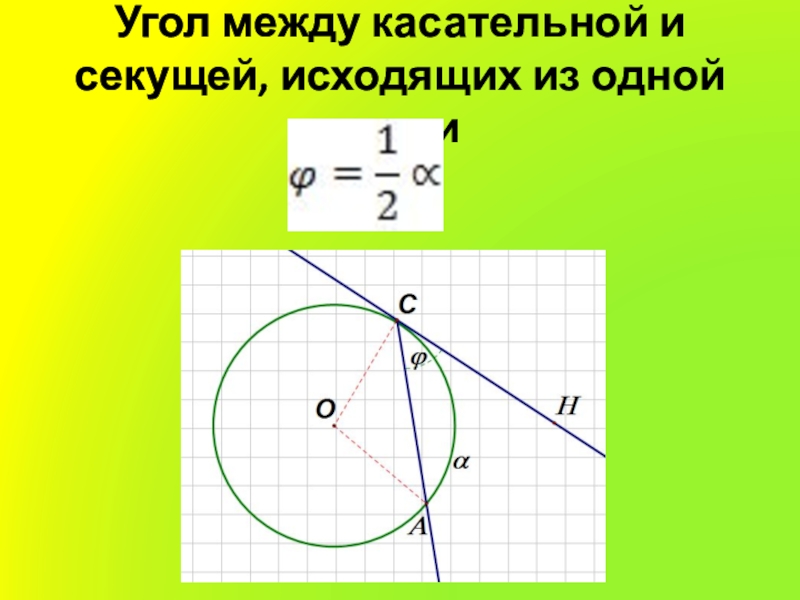
- 4. Угол между касательной и секущей, исходящих из одной точки
- 5. Угол между двумя секущими
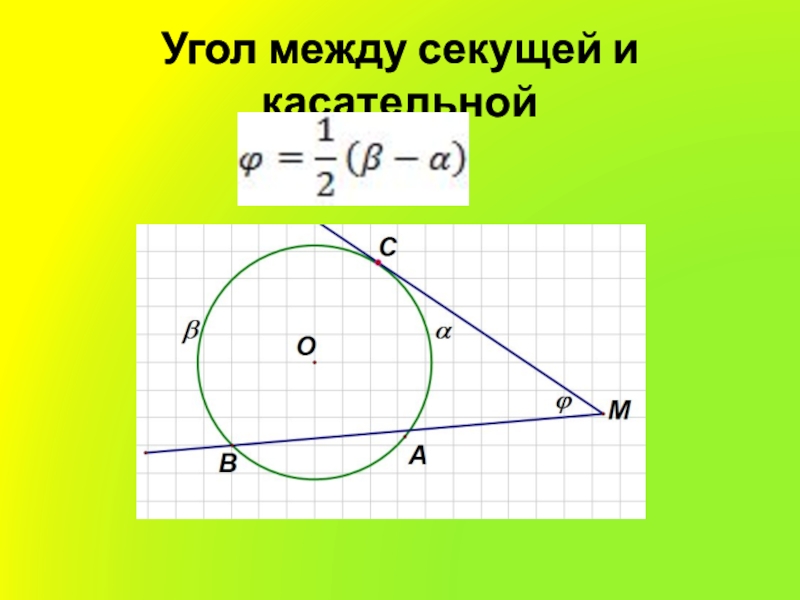
- 6. Угол между секущей и касательной
- 7. Угол между двумя касательными
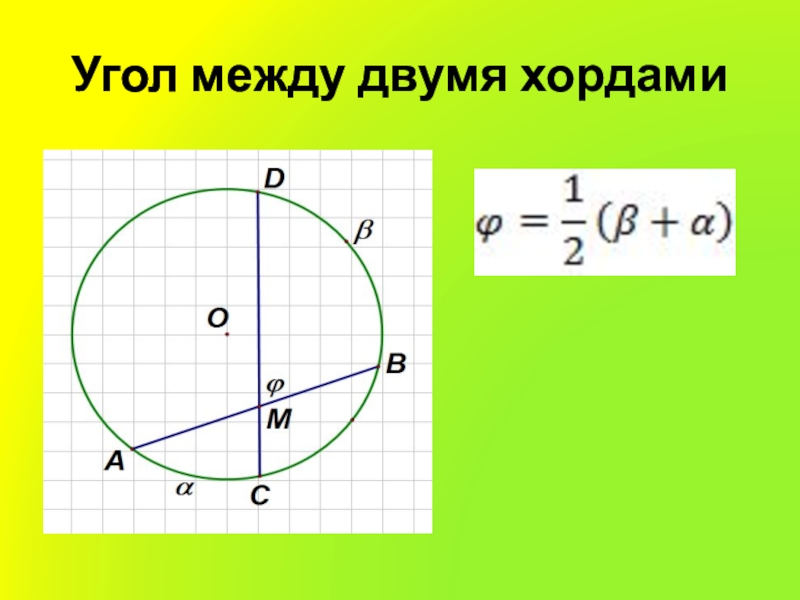
- 8. Угол между двумя хордами
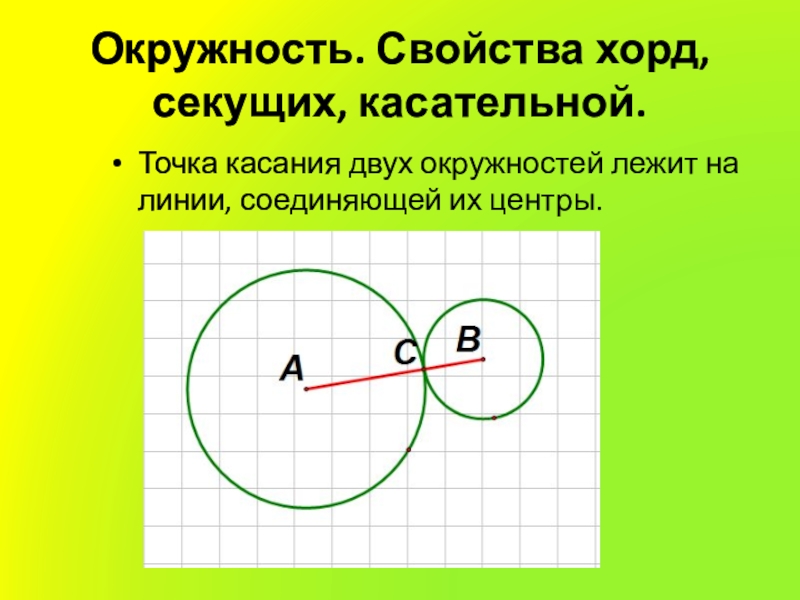
- 9. Окружность. Свойства хорд, секущих, касательной.Точка касания двух окружностей лежит на линии, соединяющей их центры.
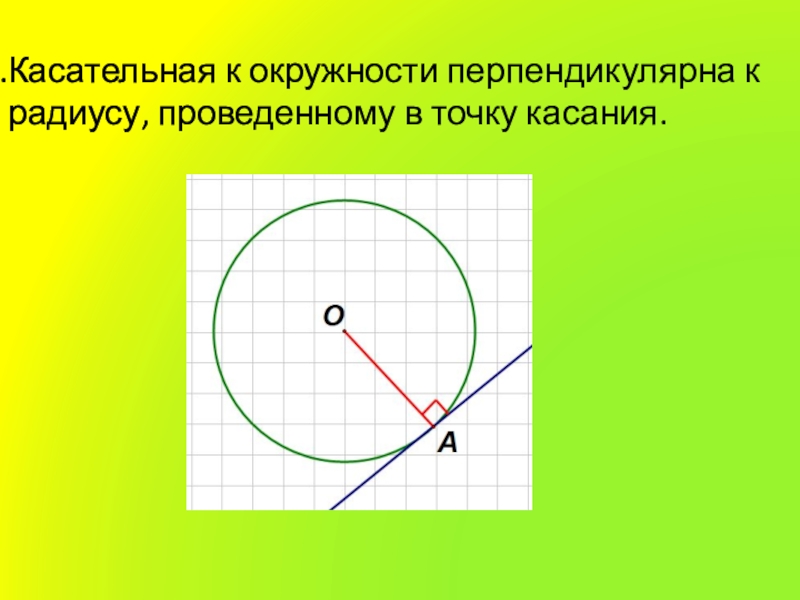
- 10. Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания.
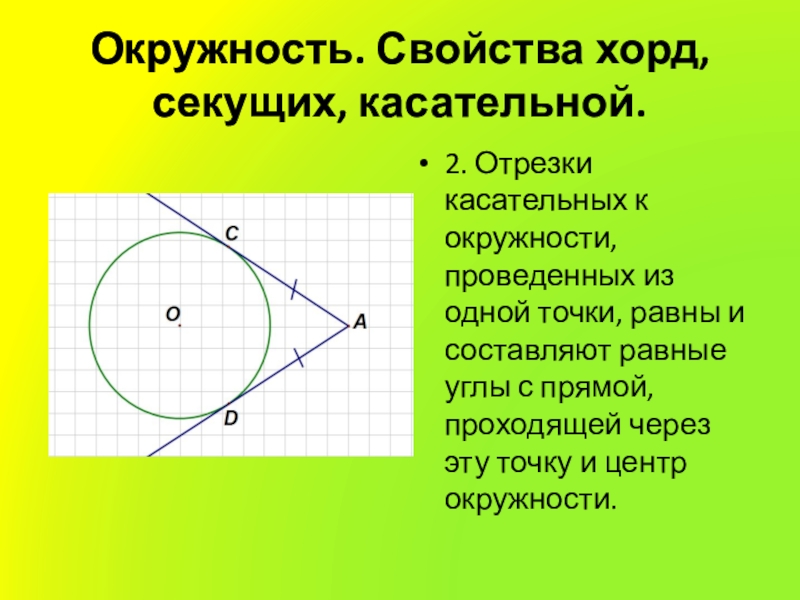
- 11. Окружность. Свойства хорд, секущих, касательной.2. Отрезки касательных
- 12. Окружность. Свойства хорд, секущих, касательной.3. Диаметр (радиус),
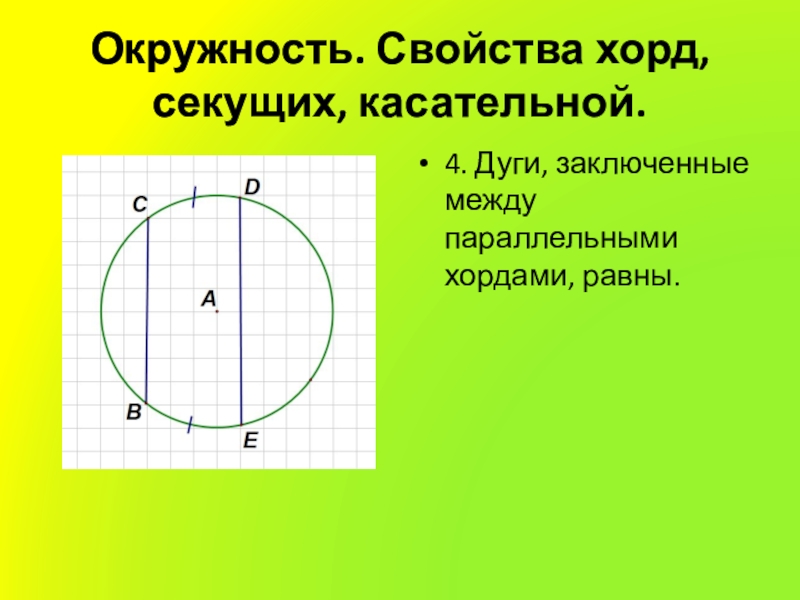
- 13. Окружность. Свойства хорд, секущих, касательной.4. Дуги, заключенные между параллельными хордами, равны.
- 14. Окружность. Свойства хорд, секущих, касательной.5. Если две
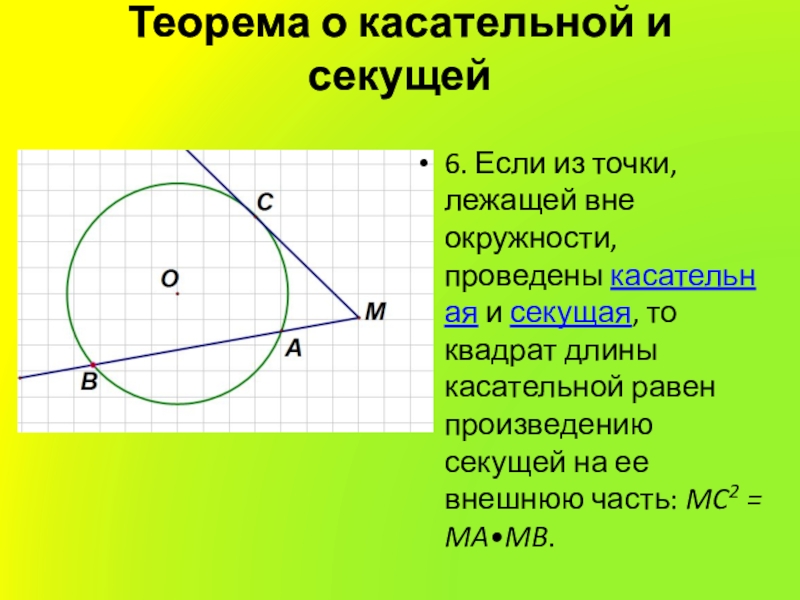
- 15. Теорема о касательной и секущей 6. Если
- 16. Теорема о секущих 7. Если из точки,
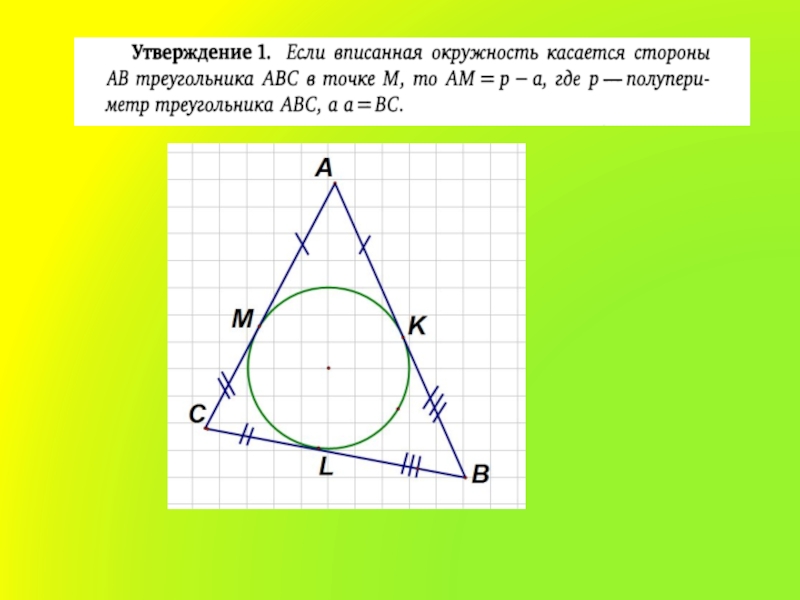
- 17. Слайд 17
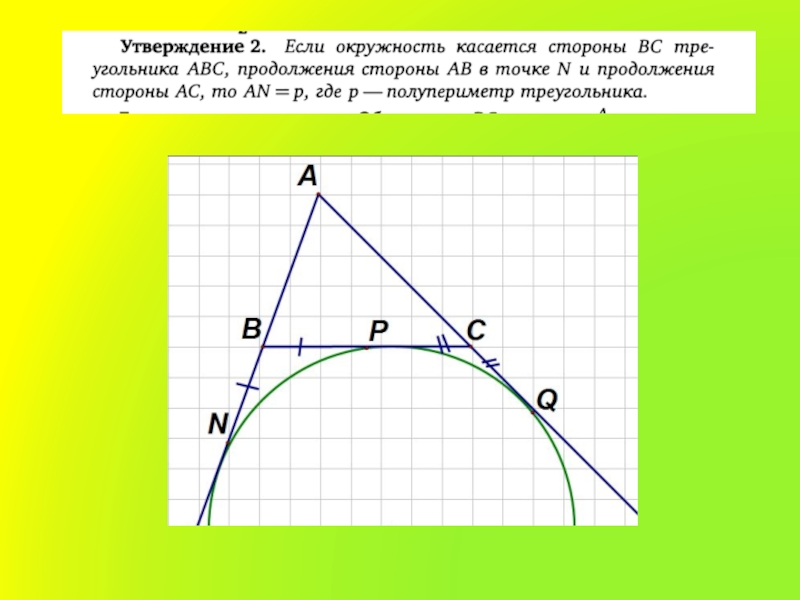
- 18. Слайд 18
- 19. Слайд 19
- 20. Слайд 20
- 21. Скачать презентанцию
Взаимное расположение прямой и окружностиПрямая может не иметь с окружностью общих точек; иметь с окружностью одну общую точку (касательная); иметь с ней две общие точки (секущая).
Слайды и текст этой презентации
Слайд 1Окружность.
Хорды, касательные, секущие.
Углы между хордами, секущими, касательными.
Планиметрия.
10
класс
Слайд 2Взаимное расположение прямой и окружности
Прямая может не иметь с окружностью
общих точек; иметь с окружностью одну общую точку (касательная); иметь
с ней две общие точки (секущая).
Слайд 9Окружность. Свойства хорд, секущих, касательной.
Точка касания двух окружностей лежит на
линии, соединяющей их центры.
Слайд 11Окружность. Свойства хорд, секущих, касательной.
2. Отрезки касательных к окружности, проведенных
из одной точки, равны и составляют равные углы с прямой,
проходящей через эту точку и центр окружности.
Слайд 12Окружность. Свойства хорд, секущих, касательной.
3. Диаметр (радиус), перпендикулярный к хорде,
делит эту хорду и обе стягиваемые ею дуги пополам.
Слайд 13Окружность. Свойства хорд, секущих, касательной.
4. Дуги, заключенные между параллельными хордами,
равны.
Слайд 14Окружность. Свойства хорд, секущих, касательной.
5. Если две хорды окружности, AB и CD пересекаются в
точке M, то произведение отрезков одной хорды равно произведению отрезков другой
хорды: AM•MB = CM•MD.
Слайд 15Теорема о касательной и секущей
6. Если из точки, лежащей вне
окружности, проведены касательная и секущая, то квадрат длины касательной равен произведению секущей на
ее внешнюю часть: MC2 = MA•MB.
Слайд 16Теорема о секущих
7. Если из точки, лежащей вне окружности, проведены
две секущие, то произведение одной секущей на её внешнюю часть равно
произведению другой секущей на её внешнюю часть. MA•MB = MC•MD.
