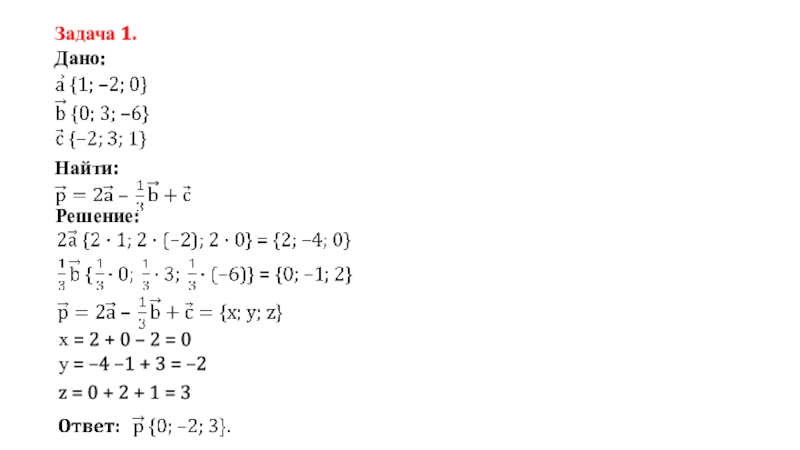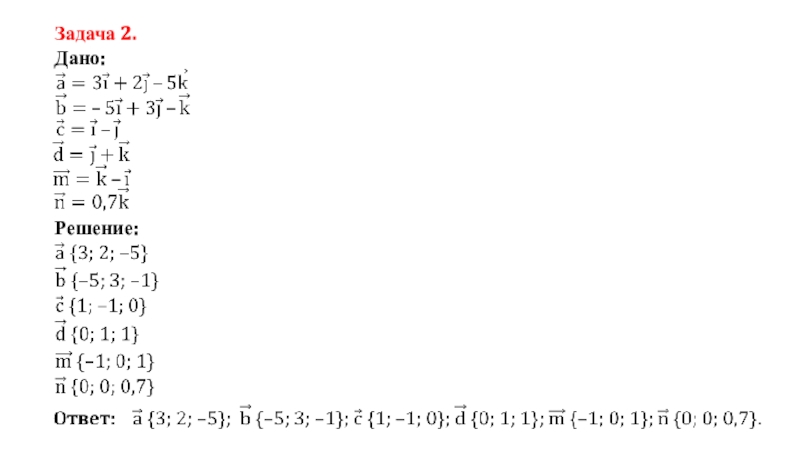Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Определение Векторы называются компланарными, если при откладывании их из одной
Содержание
- 1. Определение Векторы называются компланарными, если при откладывании их из одной
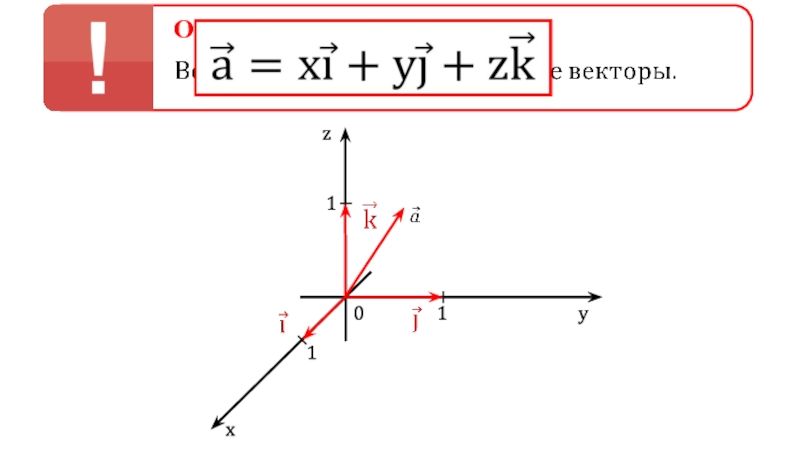
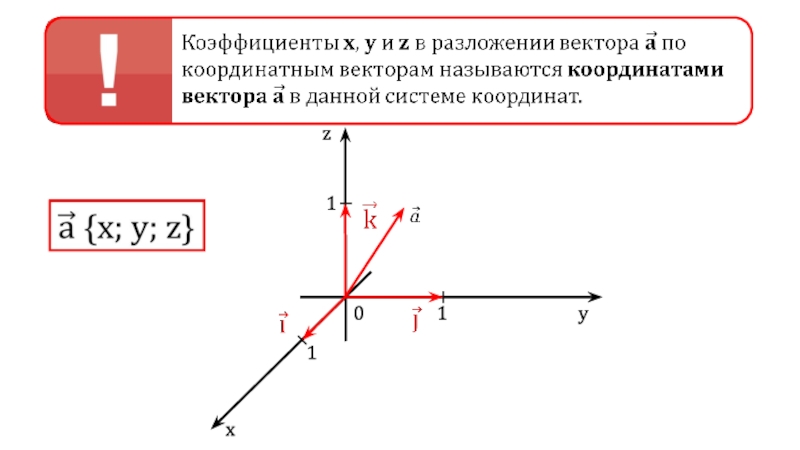
- 2. 0111zyx Определение
- 3. 0111zyx
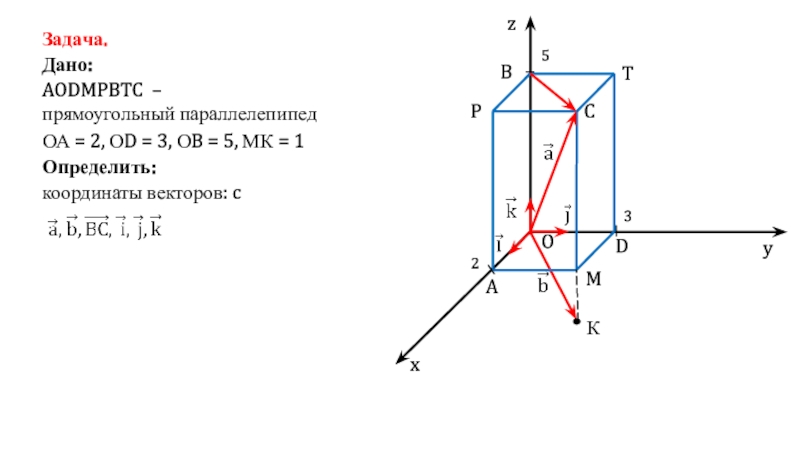
- 4. Задача.Дано:AODMPBTC – прямоугольный параллелепипедОА = 2, ОD
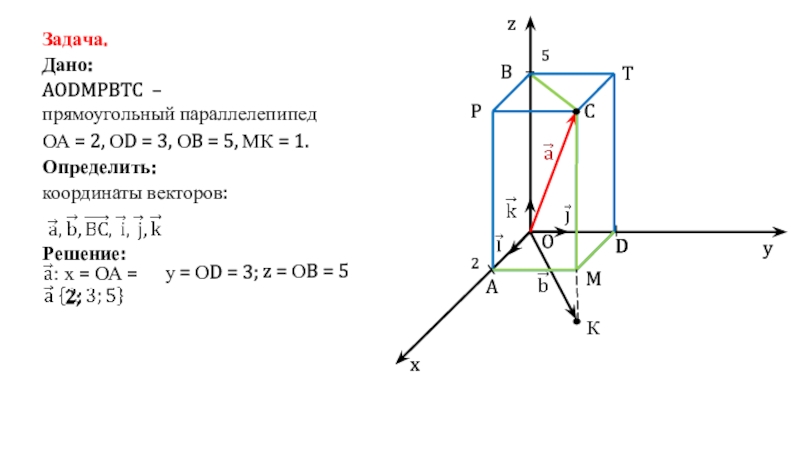
- 5. Задача.Дано:AODMPBTC – прямоугольный параллелепипедОА = 2, ОD
- 6. Задача.Дано:AODMPBTC – прямоугольный параллелепипедОА = 2, ОD
- 7. Задача.Дано:AODMPBTC – прямоугольный параллелепипедОА = 2, ОD
- 8. Задача.Дано:AODMPBTC – прямоугольный параллелепипедОА = 2, ОD
- 9. Задача.Дано:AODMPBTC – прямоугольный параллелепипедОА = 2, ОD
- 10. Задача.Дано:AODMPBTC – прямоугольный параллелепипедОА = 2, ОD
- 11. Задача.Дано:AODMPBTC – прямоугольный параллелепипедОА = 2, ОD
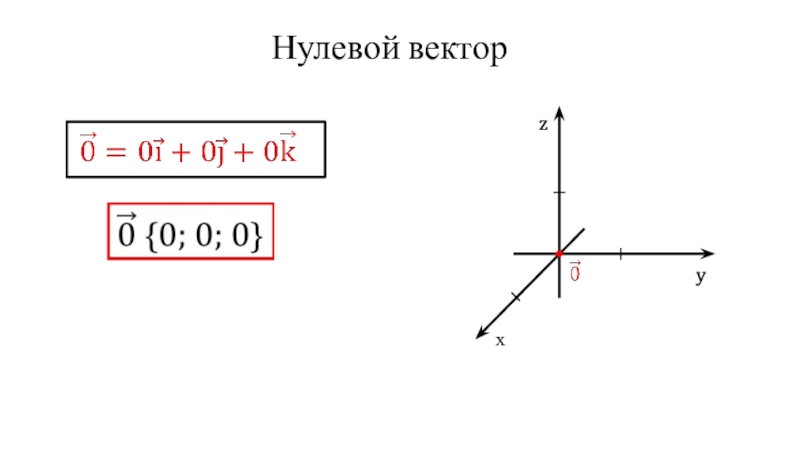
- 12. Нулевой вектор zyх
- 13. х₁ = х₂, у₁ = у₂, z₁ = z₂ Координаты равных векторов соответственно равны.
- 14. Каждая координата суммы двух или более векторов равна сумме соответствующих координат этих векторов.
- 15. Каждая координата разности двух векторов равна разности соответствующих координат этих векторов.
- 16. Каждая координата произведения вектора на число равна произведению соответствующей координаты вектора на это число.
- 17. Задача 1.Дано: Найти: Решение: х = 2 + 0
- 18. Задача 2.Дано: Решение:
- 19. Скачать презентанцию
0111zyx Определение
Слайды и текст этой презентации
Слайд 1Определение
Векторы называются компланарными, если при откладывании их из одной и
той же точки они будут лежать в одной плоскости.
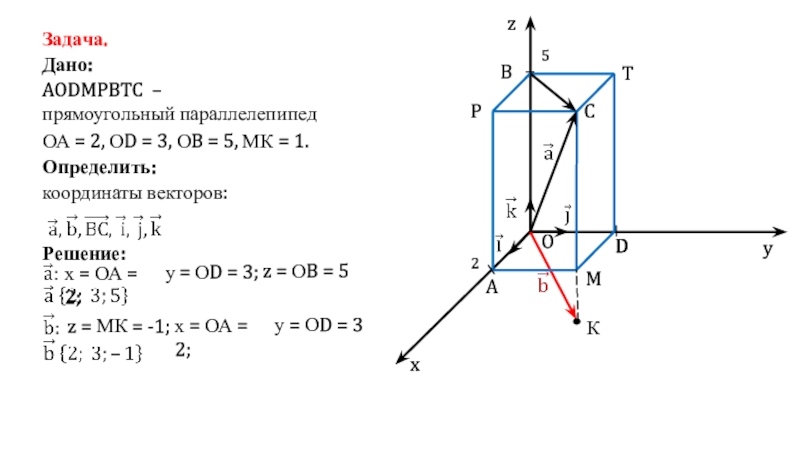
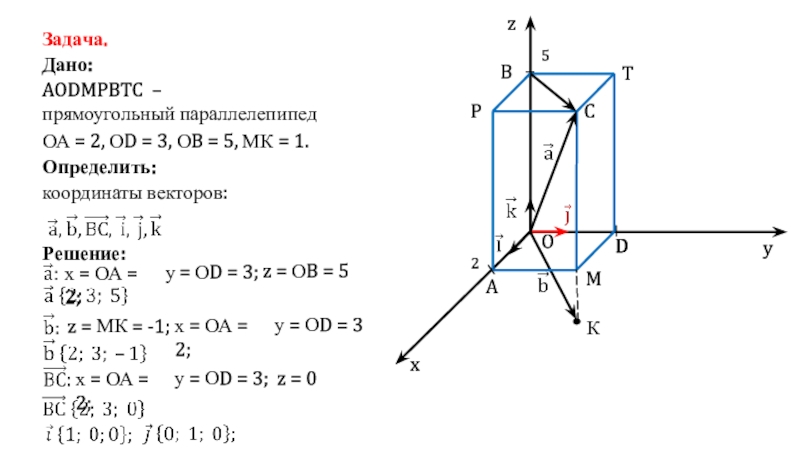
Слайд 4Задача.
Дано:
AODMPBTC –
прямоугольный параллелепипед
ОА = 2, ОD = 3, ОB
= 5, МК = 1
координаты векторов: c
Определить:
O
z
y
x
A
M
D
P
C
T
B
К
2
3
5
Слайд 5Задача.
Дано:
AODMPBTC –
прямоугольный параллелепипед
ОА = 2, ОD = 3, ОB
= 5, МК = 1.
Определить:
O
z
y
x
A
M
D
P
C
T
B
Решение:
х = ОА = 2;
у
= ОD = 3;
z = ОB = 5
координаты векторов:
К
D
2
5
Слайд 6Задача.
Дано:
AODMPBTC –
прямоугольный параллелепипед
ОА = 2, ОD = 3, ОB
= 5, МК = 1.
Определить:
O
z
y
x
A
M
D
P
C
T
B
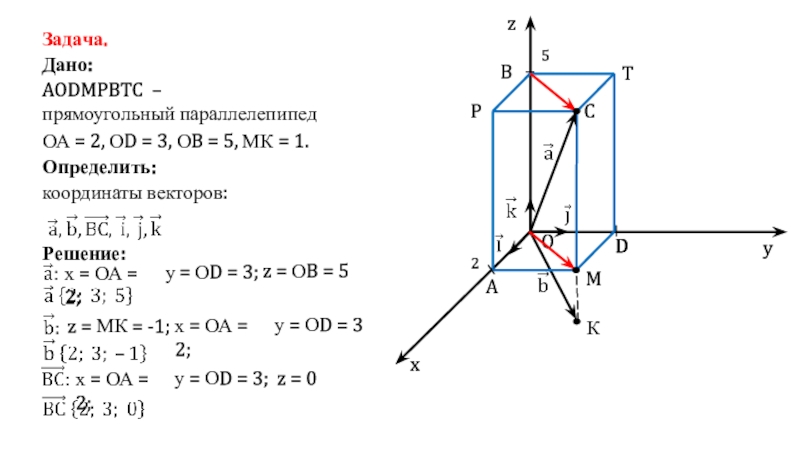
Решение:
х = ОА = 2;
у
= ОD = 3;
z = ОB = 5
координаты векторов:
К
z = МК = -1;
х = ОА = 2;
у = ОD = 3
D
2
5
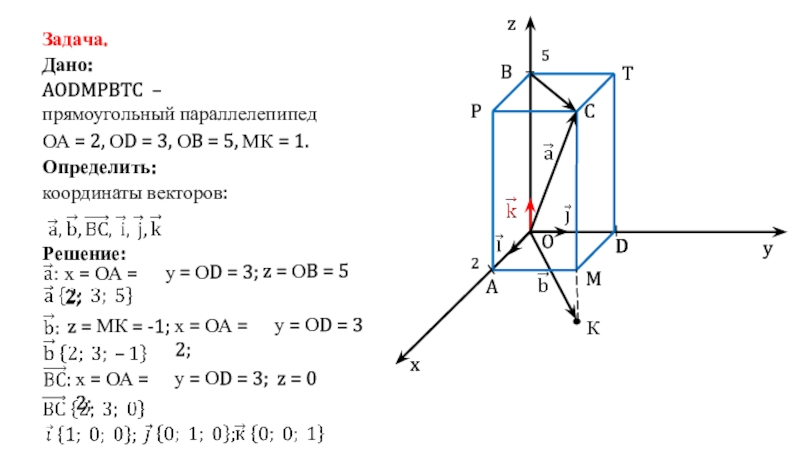
Слайд 7Задача.
Дано:
AODMPBTC –
прямоугольный параллелепипед
ОА = 2, ОD = 3, ОB
= 5, МК = 1.
Определить:
O
z
y
x
A
M
D
P
C
T
B
Решение:
х = ОА = 2;
у
= ОD = 3;
z = ОB = 5
координаты векторов:
К
z = МК = -1;
х = ОА = 2;
у = ОD = 3
D
2
5
х = ОА = 2;
у = ОD = 3;
z = 0
Слайд 8Задача.
Дано:
AODMPBTC –
прямоугольный параллелепипед
ОА = 2, ОD = 3, ОB
= 5, МК = 1.
Определить:
O
z
y
x
A
M
D
P
C
T
B
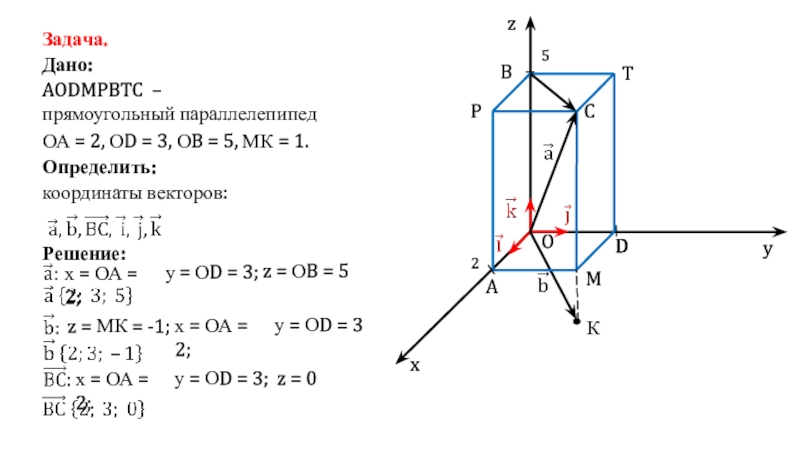
Решение:
х = ОА = 2;
у
= ОD = 3;
z = ОB = 5
координаты векторов:
К
z = МК = -1;
х = ОА = 2;
у = ОD = 3
D
2
5
х = ОА = 2;
у = ОD = 3;
z = 0
Слайд 9Задача.
Дано:
AODMPBTC –
прямоугольный параллелепипед
ОА = 2, ОD = 3, ОB
= 5, МК = 1.
Определить:
O
z
y
x
A
M
D
P
C
T
B
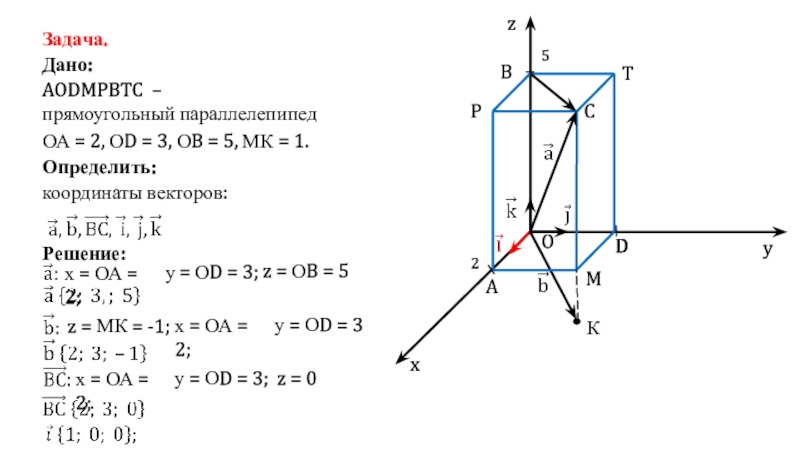
Решение:
х = ОА = 2;
у
= ОD = 3;
z = ОB = 5
координаты векторов:
К
z = МК = -1;
х = ОА = 2;
у = ОD = 3
D
2
5
х = ОА = 2;
у = ОD = 3;
z = 0
Слайд 10Задача.
Дано:
AODMPBTC –
прямоугольный параллелепипед
ОА = 2, ОD = 3, ОB
= 5, МК = 1.
Определить:
O
z
y
x
A
M
D
P
C
T
B
Решение:
х = ОА = 2;
у
= ОD = 3;
z = ОB = 5
координаты векторов:
К
z = МК = -1;
х = ОА = 2;
у = ОD = 3
D
2
5
х = ОА = 2;
у = ОD = 3;
z = 0
Слайд 11Задача.
Дано:
AODMPBTC –
прямоугольный параллелепипед
ОА = 2, ОD = 3, ОB
= 5, МК = 1.
Определить:
O
z
y
x
A
M
D
P
C
T
B
Решение:
х = ОА = 2;
у
= ОD = 3;
z = ОB = 5
координаты векторов:
К
z = МК = -1;
х = ОА = 2;
у = ОD = 3
D
2
5
х = ОА = 2;
у = ОD = 3;
z = 0
Слайд 14Каждая координата суммы двух или более векторов равна сумме соответствующих
координат этих векторов.
Слайд 15Каждая координата разности двух векторов равна разности соответствующих координат этих
векторов.
Слайд 16Каждая координата произведения
вектора на число равна произведению соответствующей координаты
вектора на это число.
