Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛ Математика ППИ ЛЕКЦИЯ №
Содержание
- 1. ОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛ Математика ППИ ЛЕКЦИЯ №
- 2. УЧЕБНЫЕ ВОПРОСЫ 3. Общая
- 3. ЛИТЕРАТУРА[1] Н.С. Пискунов. Дифференциальное и интегральное исчисления.
- 4. УЧЕБНЫЙ ВОПРОС.Общая схема применения определенного интеграла к решению геометрических и физических задач.
- 5. Общая схема применения определенного интеграла к
- 6. 2) метод дифференциала, сущность которого заключается
- 7. Пример. Пусть материальная точка М перемещается вдоль
- 8. Приближенное значение работы на [a;b] естьЭто приближенное
- 9. Пример. Вычислить силу давления воды на вертикальную
- 10. Слайд 10
- 11. Рассмотрим горизонтальную полоску толщиной dx, находящуюся на
- 12. УЧЕБНЫЙ ВОПРОСВычисление площадей плоских фигур и длин дуг плоских линий в декартовых и полярных координатах.
- 13. Вычисление площадей плоских фигур в декартовых координатах.
- 14. Пусть на [a;b] заданы непрерывные функции y=f1(x)
- 15. Пример. Найти площадь фигуры, ограниченной линиями y=x2-2,
- 16. Слайд 16
- 17. Площадь криволинейной трапеции, ограниченной кривой, заданной параметрически
- 18. Пример. Вычислить площадь фигуры, ограниченной эллипсомРешение. Найдем
- 19. Вычисление площадей в полярных координатах.
- 20. Пример. Найти площадь фигуры, ограниченной трехлепестковой розой:
- 21. Вычисление длины дуги в декартовых координатах.Теорема. Пусть
- 22. где xi-1
- 23. Пример. Найти длину дуги полукубической параболы y2
- 24. Длина дуги кривой, заданной параметрически уравнениями
- 25. Пример. Вычислить длину астроидыРешение. Так как кривая
- 26. Длина дуги кривой в полярных координатах.Пусть в
- 27. Пример. Найти длину кардиоиды r=a(1+cosφ).Решение. Кардиоида симметрична
- 28. СПАСИБО ЗА ВНИМАНИЕ
- 29. Скачать презентанцию
УЧЕБНЫЕ ВОПРОСЫ 3. Общая схема применения определенного интеграла к решению геометрических и физических задач.( ознакомительно)4. Вычисление площадей плоских фигур и длин дуг плоских линий в декартовых и полярных
Слайды и текст этой презентации
Слайд 2
УЧЕБНЫЕ ВОПРОСЫ
3. Общая схема применения определенного интеграла к решению
геометрических и физических задач.( ознакомительно)
длин дуг плоских линий в декартовых и полярных координатах.Слайд 3ЛИТЕРАТУРА
[1] Н.С. Пискунов. Дифференциальное и интегральное исчисления. Т 1. Москва:
Интеграл-Пресс, 2004. с. 340-375;
[3] Б.П. Демидович, В.А. Кудрявцев. Краткий курс
высшей математики. Москва: Издательство АСТ, 2004.. с. 253-266;[14] Л.К. Потеряева, Г.А. Таратута. Курс высшей математики IV. Челябинск: Челябинский военный авиационный краснознамённый институт штурманов, 2002 г.с. 80-94.
Слайд 4УЧЕБНЫЙ ВОПРОС.
Общая схема применения определенного интеграла к решению геометрических и
физических задач.
Слайд 5 Общая схема применения определенного интеграла к решению геометрических и
физических задач.
Пусть требуется найти значение какой-либо геометрической или физической величины
Q, связанной с отрезком [a;b] изменения независимой переменной x.Для нахождения величины можно применить один из следующих методов:
1) метод интегральных сумм, который базируется на определении определенного интеграла;
Слайд 62) метод дифференциала, сущность которого заключается в том, что
сначала составляется дифференциал искомой величины, а затем после интегрирования в
соответствующих пределах находится значение искомой величины.Слайд 7Пример.
Пусть материальная точка М перемещается вдоль оси Ox под
действие силы F=F(x). Найдем работу A силы по перемещению
M из точки x=a в точку x=b (aВыберем на каждом отрезке
[ x i-1;xi] точку ci.
Работа, совершенная силой на отрезке [ x i-1;xi], равна произведению F(ci)∙Δxi , как работа постоянной силы F(ci) на участке [ x i-1;xi].
Слайд 8Приближенное значение работы на [a;b] есть
Это приближенное равенство тем точнее,
чем меньше длина , поэтому за точное
значение работы А принимается предел интегральной суммыСлайд 9Пример. Вычислить силу давления воды на вертикальную площадку, имеющую форму
треугольника с основанием 5 м и высотой 3 м. Уровень
воды совпадает с вершиной треугольника.Решение.
По закону Паскаля давление жидкости на площадку равно ее площади S, умноженной на глубину погружения h, на плотность ρ и ускорение силы тяжести g, т.е. .
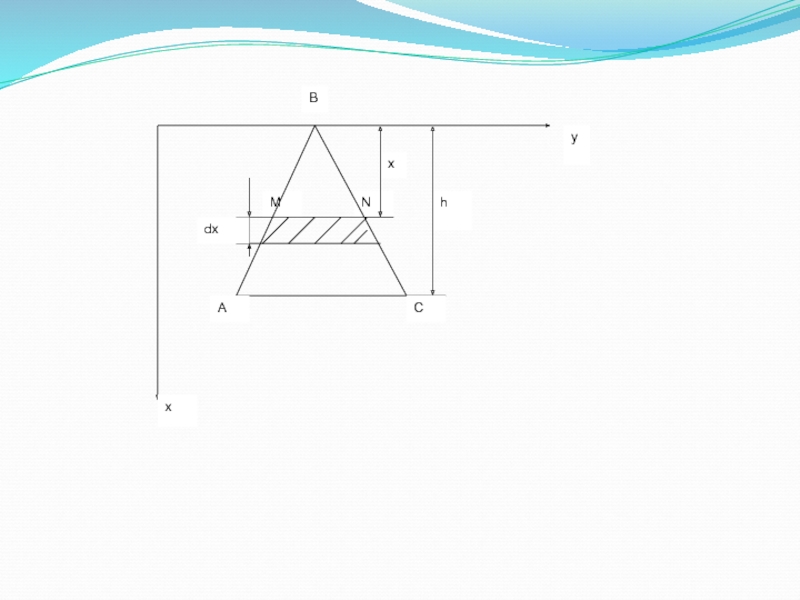
Слайд 11Рассмотрим горизонтальную полоску толщиной dx, находящуюся на глубине х .
Принимая
эту полоску за прямоугольник, находим дифференциал площади dS=MN dx. Из
подобия треугольников BMN и ABC имеем .Отсюда и
Сила давления воды на эту полоску равна dP=x dS (учитывая, что удельный вес воды равен 1). Следовательно, сила давления воды на всю площадку ABC
Слайд 12УЧЕБНЫЙ ВОПРОС
Вычисление площадей плоских фигур и длин дуг плоских линий
в декартовых и полярных координатах.
Слайд 13Вычисление площадей плоских фигур в декартовых координатах.
Если
непрерывная функция f(x)≥0 на [a;b], то площадь S криволинейной трапеции,
ограниченной линиями y= f(x); y=0 , x=a , x=b , равна интегралуЕсли же f(x)≤0 на [a;b] , то
Слайд 14Пусть на [a;b] заданы непрерывные функции y=f1(x) и y=f2(x) такие,
что f2(x)≥ f1(x). Тогда площадь S фигуры, заключенной между
кривыми y=f1(x) и y=f2(x) на отрезке [a;b] вычисляется по формулеСлайд 15Пример.
Найти площадь фигуры, ограниченной линиями y=x2-2, y=x.
Решение. Для нахождения
абсцисс точек пересечения данных кривых решим систему уравнений:
. Отсюда х1 = -1, х2= 2.Слайд 17Площадь криволинейной трапеции, ограниченной кривой, заданной параметрически
прямыми x=a, x=b
и осью Ox (х(α)=а, х(β)=b), вычисляется по формуле
,Слайд 18Пример. Вычислить площадь фигуры, ограниченной эллипсом
Решение. Найдем сначала ¼ площади
S.Здесь x изменяется от 0 до a, следовательно t изменяется
от π/2 до 0. Значит: S=πаb
Слайд 19Вычисление площадей в полярных координатах.
Площадь S плоской
фигуры, ограниченной непрерывной линией r=r(φ) и двумя лучами φ =α
и φ= β (α <β).Слайд 20Пример. Найти площадь фигуры, ограниченной трехлепестковой розой:
.
Решение.
Найдем сначала площадь половины одного лепестка розы, т.е 1/6 часть всей площади фигуры: Следовательно:
Слайд 21Вычисление длины дуги в декартовых координатах.
Теорема. Пусть кривая АВ задана
уравнением y=f(x), где f(x) - непрерывная функция, имеющая непрерывную производную
на [a;b] . Тогда дуга АВ имеет длину, равнуюДоказательство. Введем обозначение ∆yi = f(xi)-f(x i-1)
Слайд 23Пример. Найти длину дуги полукубической параболы
y2 =x3 от начала
координат до точки А(4;8) .
Решение. Имеем
Слайд 25Пример. Вычислить длину астроиды
Решение. Так как кривая симметрична относительно обеих
координатных осей, то вычислим сначала длину ее четвертой части, расположенной
в первой четверти. НаходимПараметр t будет изменяться от 0 до π/2 .
Итак,
Слайд 26Длина дуги кривой в полярных координатах.
Пусть в полярных координатах задано
уравнение кривой r=r(φ); α≤φ≤β. Если в равенствах x=rcosφ, y=rsin φ,
связывающих полярные и декартовы координаты, параметром считать угол , то кривую можно задать параметрически:Тогда
Получаем


![ОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ
ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛ
Математика ППИ
ЛЕКЦИЯ № ЛИТЕРАТУРА[1] Н.С. Пискунов. Дифференциальное и интегральное исчисления. Т 1. Москва: Интеграл-Пресс, ЛИТЕРАТУРА[1] Н.С. Пискунов. Дифференциальное и интегральное исчисления. Т 1. Москва: Интеграл-Пресс, 2004. с. 340-375;[3] Б.П. Демидович, В.А.](/img/thumbs/06565f40ad792a740972ac46262e0fd5-800x.jpg)




![ОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ
ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛ
Математика ППИ
ЛЕКЦИЯ № Приближенное значение работы на [a;b] естьЭто приближенное равенство тем точнее, чем Приближенное значение работы на [a;b] естьЭто приближенное равенство тем точнее, чем меньше длина ,](/img/thumbs/975c630d9855d583542edd537dad8aa1-800x.jpg)



![ОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ
ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛ
Математика ППИ
ЛЕКЦИЯ № Вычисление площадей плоских фигур в декартовых координатах. Если непрерывная функция Вычисление площадей плоских фигур в декартовых координатах. Если непрерывная функция f(x)≥0 на [a;b], то площадь](/img/thumbs/d99b15b766abf4a062aa88baf760b06d-800x.jpg)
![ОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ
ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛ
Математика ППИ
ЛЕКЦИЯ № Пусть на [a;b] заданы непрерывные функции y=f1(x) и y=f2(x) такие, что Пусть на [a;b] заданы непрерывные функции y=f1(x) и y=f2(x) такие, что f2(x)≥ f1(x). Тогда площадь S](/img/thumbs/7083090cbf5f0f691b5ddd1b26660702-800x.jpg)

































