Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Оптика и квантовая физика
Содержание
- 1. Оптика и квантовая физика
- 2. Оптика как раздел физикиОптикараздел физики, изучающий свойства
- 3. Свет – электромагнитная волнавакуум: другие среды:показатель преломления
- 4. Шкала электромагнитных волнГраницы между различными диапазонами условны!λф ≈ 380 нмλк ≈ 760 нмВидимый диапазон
- 5. Диапазоны электромагнитных волнДиапазонДлина волны λ, нмЕф, эВ - излучение106Рентгеновское излучение0,0012…12100… 106Ультрафиолетовое излучение12…3803,2…100Видимое излучение380…7601,6…3,2Инфракрасное излучение760…1061,2∙10-3…1,6Радиоволны>106
- 6. Спектр видимого излученияЦветДлина волны λ, нмКрасный620…760Оранжевый590…620Желтый560…590Зеленый500…590Голубой480…500Синий450…480Фиолетовый380…450КаждыйОхотникЖелаетЗнатьГдеСидитФазанСпектрраспределение интенсивности
- 7. Кривая видности
- 8. Источники светаОсновные характеристики ИСТОЧНИКОВ светаСветящиеся раскаленные твердые
- 9. Приемники светаОсновные характеристики ПРИЕМНИКОВ светаПриемники света регистрируют
- 10. ИнтерференцияДифракцияПоляризацияДавление светаВзаимодействие ЭМ волн с веществомФотоэффектТепловое излучениеВолновые
- 11. ФотометрияРаздел оптики, рассматривающий характеристики светового излучения
- 12. ФотометрияЭнергетические величиныхарактеризуют энергетические параметры безотносительно к
- 13. Энергетические величиныПоток изученияэнергия, проходящая за единицу
- 14. Энергетические величиныЭнергетическая освещенность поток излучения, приходящийся на
- 15. Эталон силы светаКанделаВ основе – эталон силы
- 16. Световые величиныСветовой потокмощность оптического излучения по
- 17. Световые величиныСветимостьвеличина, равная отношению светового потока, излучаемого
- 18. Сопоставление световых и энергетических величин
- 19. Энергетические и световые величины Поток излучения в
- 20. Интерференция света
- 21. Проявляется во взаимном усилении световых волн в
- 22. Условия наблюдения интерференцииНеобходимое условиеКогерентность волнсогласованное протеканиево времени
- 23. Принцип суперпозицииВ основе интерференции лежитПринцип суперпозицииПринцип наложения
- 24. Способы получения когерентных волн Опыт Юнга1816 г.ЭкранLdШирмы с отверстиями12x
- 25. Способы получения когерентных волн Зеркала Френеля1816 г.S1S2SЗеркало 1Зеркало 212abLdOЭкранx
- 26. Способы получения когерентных волн Бипризма ФренеляS2S1SБипризмаЭкран12dLabθ – малый преломляющий уголx
- 27. Условия интерференционных максимума и минимумаm = 0,
- 28. Расчет интерференционной картиныШиринаинтерференционной полосыРасстояние между соседними max (или min)Оптическая разность ходаПоложение minПоложение maxхr1n1r2n2
- 29. Интерференция в тонких пленкахХод лучей в плоскопараллельной
- 30. Интерференция в тонких пленках. Полосы равного наклонаИнтерференционные
- 31. Интерференция в тонких пленках. Полосы равной толщиныИнтерференционные
- 32. Интерференция в тонких пленках. Кольца Ньютона
- 33. Исследовательское задание 1Исследуйте изменение интерференционной картины
- 34. Исследовательское задание 2Исследуйте и объясните изменение ширины
- 35. Исследовательское задание 3Исследуйте интерференционные полосы равной толщины, которые можно получить с помощью ДВУХ ВЫПУКЛЫХ ЛИНЗR1R2
- 36. Исследовательское задание 4R1Исследуйте интерференционные полосы равной толщины,
- 37. Исследовательское задание 5RИсследуйте интерференционные полосы равной толщины,
- 38. Многолучевая интерференцияВозникает в тех случаях, когда поверхности,
- 39. Использование интерференцииИнтерференционная спектроскопияИнтерференция может быть использована дляизмерения
- 40. ИнтерферометрыИнтерферометрыПучок света пространственно разделяется на несколько
- 41. Интерферометр МайкельсонаL1 и L2 –длины «плеч» интерферометраДля
- 42. Интерферометр Жамена1.Пройдя через кюветы K1 и K2,
- 43. Интерференционные рефрактометрыОпределение показателей преломленияИнтерферометр Рэлея
- 44. Интерферометр Рождественского
- 45. Звездный интерферометр МайкельсонаДля измерения угловых размеров звезд
- 46. Интерферометр Фабри-Перомноголучевая интерференцияразлагает сложное излучение в
- 47. Просветление оптикитолщину пленки подбирают таким образом,
- 48. Применение интерференцииСоздание высокоотражающих поверхностейв основе – интерференция отраженных лучей на maxИнтерференционные светофильтрымноголучевая интерференция
- 49. Дифракция света
- 50. Дифракция светаПроявления дифракции:волны заходят в область геометрической
- 51. Объяснение явления дифракцииДифракционные явления были хорошо известны
- 52. Волновой принцип ГюйгенсаКаждая точка пространства, до которой
- 53. Дополнения Френеля к принципу ГюйгенсаВторичные источники не
- 54. Дифракция ФренеляДифракция от круглого отверстияДифракция в расходящихся
- 55. Результат действия зон ФренеляДействие зоны ↓ при
- 56. Результат действия зон ФренеляКоличество открытых зон
- 57. Дифракция ФренеляДифракция от диска2.пятно Пуассона (1818 г.)дифракцией
- 58. Результат действия зон ФренеляОсвещение белым светомкольца окрашеныD великАm
- 59. Дифракция на одной щелив щели укладывается
- 60. Дифракционная решеткаУравнение главных МАКСИМУМОВДифракционная решеткаСовокупность большого числа
- 61. Дифракционный спектрСпектры, начиная со второго порядка, перекрываютсяmax
- 62. Дифракционная решетка как спектральный приборОсновные характеристики
- 63. Разрешающая способность спектральных приборовРазрешающая способностьопределяет min разность
- 64. Дифракция рентгеновских лучейРентгеновское излучениеλ=0,0012…12 нм1895 г., В.РентгенБольшая
- 65. Применение дифракции рентгеновского излучениязная λизмеряя θвычисляется d+Рентгеноструктурный
- 66. Поляризация света
- 67. В любой точке поля векторы напряженности ЭП
- 68. Поляризация светаПоляризация светапроцесс ориентации вектора напряженности Е
- 69. Степень поляризации светаестественный светплоско поляризованныйчастично поляризованныйСтепень поляризацииImax
- 70. Закон МалюсаПоляризаторестественный светполяризованный светустройство для получения поляризованного
- 71. Способы получения поляризованного светаПоляризация света при отражении
- 72. Закон Брюстера 1815 г.Степень поляризации зависит от
- 73. Двойное лучепреломлениеВсе прозрачные кристаллы двойного лучепреломления?обладают способностьюэффект
- 74. Свойства обыкновенного и необыкновенного лучейЗакон преломления:для
- 75. Искусственная анизотропия при деформации. Фотоупругий эффектпрозрачные изотропные
- 76. Воздействие электрического поля1875Использование эффекта Керрадля измерения скорости
- 77. Воздействие магнитного полявозникновение двойного лучепреломления в твердых
- 78. Воздействие магнитного поляИтак,мера оптической анизотропииИскусственная оптическая анизотропиявозникает
- 79. Вращение плоскости поляризации. ПрименениеПри прохождении плоскополяризованного света
- 80. ПрименениеСоздание различных оптических эффектовВ 3D-кинематографе технология IMAX: линейная поляризация
- 81. Геометрическая оптикав основе – представление о световых лучах, как направлениях переноса световой энергии
- 82. Геометрическая оптикаГеометрическая (лучевая) оптикаРаздел физики, в котором
- 83. Законы геометрической оптикиПрямолинейного распространения светав оптически однородной
- 84. Исследовательское задание 1Исследуйте зависимость угла преломления от
- 85. Исследовательское задание 2Исследуйте явление прохождения светового луча
- 86. Исследовательское задание 3Исследуйте явление прохождения светового луча
- 87. Полное внутреннее отражениеПри переходе света из оптически
- 88. ЗеркалаХод лучей при отражении от плоского зеркалат. S' - мнимое изображение т. S
- 89. Сферические зеркалаO – оптический центрP – полюсF
- 90. Исследовательские заданияИсследуйте, как будут меняться параметры
- 91. Тонкие линзыСобирающие (a) и рассеивающие (b) линзы
- 92. Тонкие линзыПостроение изображения в СОБИРАЮЩЕЙ линзеИсследовательское задание:Исследуйте,
- 93. Ход произвольного луча в собирающей линзе
- 94. Тонкие линзыПостроение изображения в РАССЕИВАЮЩЕЙ линзеИсследовательское задание:Исследуйте,
- 95. Ход произвольного луча в рассеивающей линзе
- 96. Глаз, как оптическая система1 – склерой2 –
- 97. Оптические приборыЛупаМикроскопТелескопкоэффициент увеличенияпредмет – между фокусом и линзой
- 98. Оптические приборыФотоаппаратПроектор
- 99. Аберрации оптических системСферическая аберрацияПроявляется при отображении точек,
- 100. Аберрации оптических системХроматическая аберрацияДля разных λ возникают
- 101. Аберрации оптических системизображение точки, расположенной близко к
- 102. Аберрации оптических системКомаПри прохождении широкого пучка, не
- 103. Взаимодействие света с веществом
- 104. Взаимодействие света с веществом?веществоЗависимость скорости распространения световых
- 105. Дисперсия светаДетальные экспериментальные наблюдения дисперсии света –
- 106. Дисперсия света в призме1угол отклонения лучей призмой
- 107. Радуга
- 108. Схема образования радугисферическая каплявходящий луч светапреломлениеполное внутреннее
- 109. РадугаСхема образования радуги:сферическая каплявнутреннее отражениепервичная радугапреломлениевторичная радугавходящий
- 110. Дифракционный и дисперсионный спектрыРазлагая свет в спектр
- 111. Применение дисперсииПризменные спектрографыНормальная дисперсиянеобходимость градуировкиразличная дисперсия
- 112. Объяснение явления дисперсии светаТеория МаксвеллаВ оптической области
- 113. Качественное объяснение дисперсиие- в атоме диэлектрика под
- 114. Количественное объяснение дисперсииПод действием ЭМ волны происходит
- 115. Дисперсия веществафизическая величина, показывающая, как быстро изменяется
- 116. Поглощение (абсорбция) светаПоглощение (абсорбция) светаявление уменьшения энергии
- 117. Закономерности поглощения света — коэффициент поглощения Закон
- 118. Коэффициент поглощения зависит от:интенсивности света (для малых
- 119. Применение явления поглощениястекло, слабо поглощающее красные
- 120. Виды спектровСпектр поглощениянагревательэкранhνвеществоэкранвеществосовокупность частот (длин волн), поглощаемых (излучаемых) данным веществомСпектрСпектр излученияhνQ
- 121. Виды спектров
- 122. Виды спектроводноатомные газы и пары металлов10–12-10–11
- 123. Примеры линейчатых спектров
- 124. Примеры сплошных спектровПочти все звезды имеют линии поглощения в спектре
- 125. Спектральный анализФизические методы определения состава вещества,
- 126. Излучение Вавилова-ЧеренковаСвечение сиреневатого оттенка, возникающее в результате
- 127. Рассеяние светаРассеяние светанесобственное свечение вещества при
- 128. Рассеяние светаРассеяние происходит в резко неоднородных (мутных)
- 129. Молекулярное рассеяние светаМолекулярное рассеяние светаРассеяние света чистыми
- 130. Цвета тел Для того чтобы возникло ощущение
- 131. Определение скорости света
- 132. Скорость света. Методы измерения скорости света Скорость
- 133. Астрономические методы измерения скорости светаОснова методаМетод Ремера,
- 134. Лабораторные методы измерения скорости светаМетод зубчатого колеса (метод Физо)Метод ячеек Керра
- 135. Лабораторные методы измерения скорости светаМетод световой или
- 136. Эффект Доплера
- 137. Эффект ДоплераПродольный эффект ДоплераПоперечный эффект ДоплераЭффект
- 138. Экспериментальная проверка эффекта Доплера эффекта Доплера НЕТэффекта
- 139. Значение и применение эффекта ДоплераРадиолокацияДля измерения скорости
- 140. Абсо́рбция (лат. absorptio ← absorbere — «поглощать»)
- 141. Фотоэффект
- 142. ФотоэффектВырывание электронов из металлов под действием светаметаллическая
- 143. Виды фотоэффектавырывание электронов из металла, под действием
- 144. Законы фотоэффектаМаксимальная кинетическая энергия вырываемых светом электронов
- 145. Уравнение Эйнштейна для внешнего фотоэффектаЭнергия фотона
- 146. Законы фотоэффектаУравнение Эйнштейна для фотоэффектаМаксимальная кинетическая энергия
- 147. Объяснение явленияСилы, возвращающие электроны вглубь металла:1. притяжение
- 148. Вольтамперная характеристикаНапряжение, при котором анодный ток прекращаетсяток
- 149. Схема опытаПоглотив фотон, электрон получает от
- 150. Практическое применение фотоэффектаФотоэлементы разных типовВакуумные фотоэлементыГазонаполненные фотоэлементы
- 151. Давление света
- 152. Давление светадавление, производимое светом на отражающие
- 153. Объяснение давления светаДавление света можно объяснить как
- 154. Объяснение давления светаДавление света можно объяснить как
- 155. Рентгеновское излучение
- 156. Рентгеновское излучение 1895 г.Свойства рентгеновского излученияБольшая проникающая
- 157. Тормозное рентгеновское излучение Тормозное рентгеновское излучениеПо закону
- 158. Характеристическое рентгеновское излучение возникает при достаточно больших
- 159. Возникновение характеристического излученияОбъяснение возникновения характеристического излучения по
- 160. Эффект Комптона
- 161. Эффект Комптона не зависит от природы рассеивающего
- 162. Эффект Комптона
- 163. Эффект КомптонаЗначение комптоновского эффектаподтверждает квантовую фотонную природу
- 164. Тепловое излучение
- 165. Тепловое излучениеИзлучение тел, вызванное их нагреваниемТепловое излучениеУскоренно
- 166. Характеристики теплового излученияфизическая величина, численно равная энергии
- 167. Абсолютно черное телоТело, обладающее свойством поглощать все
- 168. Закон КирхгофаНЕ зависит от природы телаОтношение спектральной
- 169. Следствия из закона Кирхгофа1.излучениепоглощениеМаксимальной спектральной плотностью энергетической
- 170. Законы теплового излучения1879 – эксперимент – Стефан1884
- 171. Закон смещения ВинаПри повышении температуры , соответствующая
- 172. Ультрафиолетовая катастрофаФормула Рэлея-ДжинсаЭнергия, излучаемая с 1
- 173. Квантовая гипотезаМакс ПланкПредложил согласующееся с опытными данными
- 174. Законы теплового излучения с точки зрения квантовой
- 175. Элементы квантовой физики
- 176. Элементы квантовой физикиПредставления о строении атомаПространственная форма s-, p-, d-, f- атомных орбиталей
- 177. Элементы квантовой физикиПостулаты БораСуществуют такие стационарные состояния
- 178. Элементы квантовой физикиВолновые свойства частицВолновые свойства присущи
- 179. Соотношение неопределенностей ГейзенбергаДвойственная корпускулярно-волновая природа частиц веществанельзя
- 180. Особенности квантовой теорииЭкспериментальное подтверждение идеи де Бройля
- 181. Волновая функцияЧтобы волновая функция являлась объективной характеристикой
- 182. Уравнение Шрёдингера1926 г.Статистическое толкование волн де
- 183. Уравнение Шрёдингера для стационарных состоянийСтационарные состояниясостояния
- 184. Применение уравнения Шрёдингерауравнение Шрёдингера для электрона в
- 185. Электрон в одномерной потенциальной ямеРешая уравнение Шрёдингера,
- 186. Линейный гармонический осцилляторРешая данное уравнение, получаем:n =
- 187. Дополнительные слайды
- 188. Разность фаз. Оптическая разность ходаРазность фазУравнение гармонического колебанияОптическая разность хода
- 189. Взаимодействие ЭМ волны с металлом 103—105
- 190. Александр Григорьевич СтолетовРоссийский физик.Получил кривую намагничивания железа
- 191. Альберт ЭйнштейнФизик-теоретик, один из основателей современной теоретической физикилауреат Нобелевской
- 192. Макс ПланкМакс Карл Эрнст Людвиг Планк[1] (нем. Max Karl
- 193. Иоганн КеплерНемецкий математик, астроном, оптик и астролог.Открыл
- 194. Густав Людвиг ГерцНемецкий физик, лауреат Нобелевской премии
- 195. Луиджи Гальвани1737-1798ИталияАлександр Григорьевич Столетов1839-1896Россия, МоскваФилипп Эдуард Антон фон Ленард 1862-1947 ГерманияАльберт ЭйнштейнAlbert Einstein1879-1955Германия, США
- 196. Йозеф СтефанАвстрийский физик и математикЧлен Австрийской академии
- 197. нем. Ludwig Eduard Boltzmann, 20 февраля 1844,
- 198. Вильгельм Карл Вернер Отто Фриц Франц ВИННемецкий
- 199. Эрвин ШрёдингерАвстрийский физик-теоретикАвтор ряда фундаментальных результатов
- 200. Джон Уильям РэлейРэлей (Стретт) Джон Уильям (1842–1919)
- 201. Джинс Джеймс ХопвудДжинс Джеймс Хопвуд (1877–1946) –
- 202. Джон Уильям Стретт он же Барон Рэлей
- 203. Дмитрий Сергеевич РождественскийИсследование аномальной дисперсиисоздал Государственный оптический
- 204. Этьен Луи Малюс1775-1812 ФранцияЭтьен Луи Малюс
- 205. Дэйвид Брюстер1781-1868 ШотландияDavid Brewster
- 206. Использованные источникиТрофимова Т.И. Курс физикиКостко О.К. Физика
- 207. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Оптика
и квантовая физика
Бахтина Елена Юрьевна,
elbakh@gmail.com
к.ф.-м.н., доц. каф. физики
Московский
государственный строительный университет
Слайд 2Оптика как раздел физики
Оптика
раздел физики, изучающий свойства и физическую природу
света, а также законы его распространения
и взаимодействия с веществом
Геометрическая
(лучевая) оптикав основе – представление о световых лучах,
как направлениях переноса световой энергии
Волновая оптика
изучает явления, в которых проявляются волновые
свойства света – интерференция, дифракция, поляризация и др.
Фотометрия
рассматривает энергетические характеристики светового излучения в процессах его испускания, распространения
и взаимодействия с веществом
Квантовая оптика
изучает явления, в которых проявляются корпускулярные свойства света, а также взаимодействие света с веществом,
в основе – понятие фотона, как кванта ЭМ излучения
Оптика двужущихся сред
Экспериментальные основы специальной теории относительности
физическая оптика
Слайд 3Свет – электромагнитная волна
вакуум:
другие среды:
показатель преломления среды
Скорость ЭМ волн
в вакууме
В любой точке векторы
напряженности ЭП Е,
магнитной индукции В
и скорости распространения волны υ
┴ между собой, образуя правовинтовую систему
ЭМ волна поперечная
ε0 = 8,85419·10–12 Ф/м
μ0 = 1,25664·10–6 Гн/м
n показывает, во сколько раз скорость света в среде МЕНЬШЕ, чем в вакууме
Скорость ЭМ волн
в среде
!
С =299 792 456,2 1,1 м/с
Ивенсон, США (1972)
Слайд 4Шкала электромагнитных волн
Границы между различными диапазонами условны
!
λф ≈ 380 нм
λк
≈ 760 нм
Видимый диапазон
Слайд 5Диапазоны
электромагнитных волн
Диапазон
Длина волны λ, нм
Еф, эВ
- излучение
106
Рентгеновское излучение
0,0012…12
100… 106
Ультрафиолетовое
излучение
12…380
3,2…100
Видимое излучение
380…760
1,6…3,2
Инфракрасное излучение
760…106
1,2∙10-3…1,6
Радиоволны
>106
Слайд 6Спектр видимого излучения
Цвет
Длина волны λ, нм
Красный
620…760
Оранжевый
590…620
Желтый
560…590
Зеленый
500…590
Голубой
480…500
Синий
450…480
Фиолетовый
380…450
Каждый
Охотник
Желает
Знать
Где
Сидит
Фазан
Спектр
распределение интенсивности ЭМ волн
по
длинам или частотам
Монохроматическая волна
волна, имеющая постоянную амплитуду и постоянную частоту
Слайд 8Источники света
Основные характеристики ИСТОЧНИКОВ света
Светящиеся раскаленные твердые и жидкие тела
излучение
за счет тепловой энергии
лампы накаливания, расплавленный металл
Светящиеся разряженные газы
излучение за
счет возбуждения электронамиртутная лампа
Светящиеся разряженные газы
излучение за счет разного рода люминесценции – катодолюминесценция, химическая, механическая
люминесцентные лампы
Лазеры
источники когерентного монохроматического излучения
спектральный состав излучения
световая отдача
яркость источника
Слайд 9Приемники света
Основные характеристики ПРИЕМНИКОВ света
Приемники света регистрируют энергию светового излучения
приемники,
использующие фотоэлектрические явления
фотоумножитель, фотодиод, фоторезистор
принимаемый спектр
инерционность
интегральная чувствительность
приемники, использующие фотохимические явления
фотобумага,
фотопленкаприемники, использующие люминесценцию
экраны, светящиеся под действием света
приемники, использующие термоэлектрические явления
термопары, термостолбики
человеческий глаз
Слайд 10Интерференция
Дифракция
Поляризация
Давление света
Взаимодействие
ЭМ волн с веществом
Фотоэффект
Тепловое излучение
Волновые свойства
Корпускулярные свойства
Эффект Комптона
Фотометрия
Геометрическая оптика
Рентгеновское
излучение
Эффект Доплера
Определение скорости света
Элементы квантовой физики
Слайд 11Фотометрия
Раздел оптики, рассматривающий характеристики светового излучения
в процессах его испускания,
распространения
и взаимодействия с веществом
Слайд 12Фотометрия
Энергетические величины
характеризуют энергетические параметры безотносительно
к его действию на приемники
излучения
Световые величины
характеризуют физиологическое действие света, оцениваемое
по воздействию на
глаз и другие селективные приемники светас учетом спектральной чувствительности
не зависящие от частоты
объективные
субъективные
Слайд 13Энергетические величины
Поток изучения
энергия, проходящая
за единицу времени
через выбранную площадку
поток
излучения, распространяющийся внутри единичного телесного угла dΩ
Сила излучения
Понятие силы излучения
относится только к точечному источнику светаТочечный источник
если его размеры малы по сравнению с расстоянием
до наблюдателя
Энергетическая сила света
ватт на стерадиан
Слайд 14Энергетические величины
Энергетическая освещенность
поток излучения, приходящийся на единицу площади
Облученность
Энергетическая яркость
величина,
равная отношению энергетической силы света элемента излучающей поверхности к площади
Лучистость
Энергетическая светимость
поток излучения, исходящий с единицы площади
характеризует приемник
характеризует источник
характеризует источник
Слайд 15Эталон силы света
Кандела
В основе – эталон силы света – КАНДЕЛА
равна силе света, излучаемого в заданном направлении источником монохроматического излучения
частотой 540∙1012 Гц, энергетическая сила света которого в этом направлении составляет 1/683 Вт/срКандела от лат. candela — свеча
cd, кд
выбранная частота соответствует зеленому цвету
В современном определении коэффициент 1/683 выбран
т.о., чтобы новое определение соответствовало старому
сила света, излучаемого абсолютно чёрным телом нормально () к поверхности площадью 1/60 см²
при температуре плавления платины (2042,5 К)
Свеча
(до 1967 г.)
Сила света типовых источников
Слайд 16Световые величины
Световой поток
мощность оптического излучения
по вызываемому им световому ощущению
(по его действию на селективный приемник света с заданной спектральной
чувствительностью)люмен
Сила света
величина равная отношению светового потока
к телесному углу, в котором распределен этот поток
кандела
1 лм – световой поток, излучаемый точечным источником света силой света 1 кд внутри телесного угла 1 ср
1 лм=1 кд∙ср
Слайд 17Световые величины
Светимость
величина, равная отношению светового потока, излучаемого поверхностью источника,
к площади
этой поверхности
Яркость
величина, равная отношению силы света в данном направлении к
площади, данному направлению Освещенность
величина, равная отношению светового потока, падающего на поверхность, к площади этой поверхности
люкс
Освещенность равна 1 лк, если поверхностная плотность светового потока в 1 лм равномерно распределена по площади S=1 м2
показывает, насколько сильно освещена поверхность
Слайд 19Энергетические и световые величины
Поток излучения в 0,0016 Вт при
λ=555 нм
вызывает световое ощущение в 1 Лм
Переход от энергетических
фотометрических величин
к световым и обратно:Слайд 21Проявляется во взаимном усилении световых волн в одних точках пространства
и ослаблении – в других
Интерференция света
От лат. inter – взаимно,
между собой
и ferio – ударяю, поражаю —
взаимоподавление одновременно осуществляющихся процессовЧастный случай общего явления интерференции волн
Явление пространственного перераспределения энергии
светового излучения при наложении
двух или нескольких световых волн
Наблюдается устойчивая картина чередующихся максимумов
и минимумов интенсивности света
Слайд 22Условия наблюдения интерференции
Необходимое условие
Когерентность волн
согласованное протекание
во времени и пространстве
нескольких волновых
процессов
При суперпозиции
(наложении) таких волн
и наблюдается интерференционная картина
У двух разных
источников света никогда НЕ сохраняется постоянная разность фаз волнИнтерференцию можно наблюдать также
при разделении первоначального
луча света на два луча
монохроматичность волн
1.
постоянство разности фаз
2.
параллельность
световых векторов
3.
их лучи НЕ интерферируют
Слайд 23Принцип суперпозиции
В основе интерференции лежит
Принцип суперпозиции
Принцип наложения электрических и магнитных
полей без их искажения
S1
S2
I2
I1
A
экран
S1, S2 – источники света
I1, I2 –
интенсивности световых волнr1, r2 – геометрическая длина пути
– оптическая разность хода
n1r1
n2r2
= n2r2 - n1r1
n1, n2 – показатели преломления сред
n1r1 – оптическая длина пути
Слайд 25Способы получения когерентных волн
Зеркала Френеля
1816 г.
S1
S2
S
Зеркало 1
Зеркало 2
1
2
a
b
L
d
O
Экран
x
Слайд 26Способы получения когерентных волн
Бипризма Френеля
S2
S1
S
Бипризма
Экран
1
2
d
L
a
b
θ – малый преломляющий угол
x
Слайд 27Условия интерференционных максимума и минимума
m = 0, 1, 2, …
Смена
min на max происходит при изменении Δ на λ/2
Слайд 28Расчет интерференционной картины
Ширина
интерференционной полосы
Расстояние между соседними max (или min)
Оптическая
разность
хода
Положение min
Положение max
х
r1n1
r2n2
Слайд 29Интерференция в тонких пленках
Ход лучей в плоскопараллельной пластине
h – толщина пластинки
n – показатель преломления
β – угол
преломленияполосы равного наклона
(α = const)
Типы интерференции
в тонких пленках
полосы равной толщины
(h = const)
кольца Ньютона
λ/2 обусловлена
потерей полуволны
при отражении света
от оптически более плотной среды (в т. А)
Слайд 30Интерференция в тонких пленках. Полосы равного наклона
Интерференционные полосы, возникающие
в
результате наложения лучей, падающих
на плоскопараллельную пластинку под одинаковыми углами
Толщина
пластины одинаковаяСлайд 31Интерференция в тонких пленках. Полосы равной толщины
Интерференционные полосы, возникающие в
результате интерференции от мест одинаковой толщины
Угол падения лучей одинаковый
Слайд 32Интерференция в тонких пленках. Кольца Ньютона
для
m-го светлого кольца
для m-го темного кольца
m = 0,1,2,…
max интерференции в
отраженном светеmin интерференции в проходящем свете
R – радиус кривизны линзы
в отраженном свете:
Исследовательские задания
Слайд 33Исследовательское задание 1
Исследуйте изменение интерференционной картины
колец Ньютона в отраженном
и проходящем свете при медленном удалении линзы от пластинки
h
Направление движения
линзыСлайд 34Исследовательское задание 2
Исследуйте и объясните изменение ширины интерференционных
колец Ньютона
в отраженном и проходящем свете при увеличении радиуса интерференционного кольца
r
δx
Слайд 35Исследовательское задание 3
Исследуйте интерференционные полосы равной толщины, которые можно получить
с помощью ДВУХ ВЫПУКЛЫХ ЛИНЗ
R1
R2
Слайд 36Исследовательское задание 4
R1
Исследуйте интерференционные полосы равной толщины,
которые можно получить
с
помощью ВЫПУКЛОЙ и ВОГНУТОЙ ЛИНЗ
R2
Слайд 37Исследовательское задание 5
R
Исследуйте интерференционные полосы равной толщины,
которые можно получить
с
помощью
ЦИЛИНДРИЧЕСКОЙ ЛИНЗЫ
и пластины
пластина
цилиндрическая линза
Слайд 38Многолучевая интерференция
Возникает в тех случаях, когда поверхности, ограничивающие пленку или
пластинку,
обладают высоким коэффициентом отражения
1, 2, 3, …, N –
когерентные лучиСлайд 39Использование интерференции
Интерференционная спектроскопия
Интерференция может быть использована для
измерения длин волн
подтверждения
волновой природы
света
измерения показателей преломления
получения высокоотражающих покрытий
Просветление оптики
контроля качества обработки поверхностей
интерференция
в
тонких пленкахулучшения качества оптических приборов
Интерференционные рефрактометры
с точностью
до 10-8 м
Слайд 40Интерферометры
Интерферометры
Пучок света пространственно разделяется
на несколько когерентных пучков,
которые проходят
различные оптические пути и при наложении создают интерференционную картину, по которой
можно установить смещение фаз пучковПо числу
интерферирующих
пучков света
двухлучевые
многолучевые
Интерферометр
измерительный прибор, использующий явление интерференции
Слайд 41Интерферометр Майкельсона
L1 и L2 –
длины «плеч» интерферометра
Для исследования поверхности создается
тонкая клиновидная прослойка воздуха между поверхностью образца S2 и изображением
зеркала S’1Неровности поверхности размером до 10-6 см вызывают заметные искривления интерференционных полос, образующихся при отражении света от проверяемой поверхности и поверхности зеркала
сдвиг интерференционных полос
Используется в
фурье-спектроскопии
Для измерения спектральных характеристик небесных тел
Слайд 42Интерферометр Жамена
1.
Пройдя через кюветы K1 и K2, пучки, отразившиеся от
поверхностей пластины P2, попадают в зрительную трубу T, где интерферируют,
образуя полосы равного наклонаПучок света S после отражения от передней и задней поверхностей пластины P1 разделяется на два пучка S1 и S2
Если одна из кювет наполнена веществом с показателем преломления n1, а другая с n2, то по смещению интерференционной картины на число полос m
по сравнению со случаем, когда обе кюветы наполнены одним и тем же веществом, можно найти неизвестный n
2.
3.
Измерение
длин волн
Измерение
показателей преломления
Контроль
качества обработки поверхностей
Слайд 45Звездный интерферометр Майкельсона
Для измерения угловых размеров звезд
и угловых расстояний
между двойными звездами
Свет от звезды, отразившись от зеркал M1, M2,
M3, M4, образует
в фокальной плоскости телескопа интерференционную картинуУгловое расстояние между соседними максимумами q = l/D
При наличии двух близких звезд, находящихся
на угловом расстоянии j,
в телескопе образуются две интерференционные картины, также смещенные на угол j
определение j
Изменяя D добиваются наилучшей видимости картины, что будет при условии j = 1/2q = l/2D
Слайд 46Интерферометр Фабри-Перо
многолучевая интерференция
разлагает сложное излучение
в спектр
интерференционный спектральный прибор высокой
разрешающей силы
используется
для исследования спектров
в видимой, ИК
и сантиметровой
областях длин волнРазновидность интерферометра Фабри-Перо
оптические резонаторы лазеров,
излучающая среда которых располагается
между зеркалами интерферометра
Слайд 47Просветление оптики
толщину пленки
подбирают таким образом, чтобы для отраженного света
выполнялось условие интерференционного минимума
для длин волн средней части спектра (λз~555
нм)потери энергии
при отражении уменьшаются
доля энергии проходящего света возрастает
Слайд 48Применение интерференции
Создание высокоотражающих поверхностей
в основе – интерференция отраженных лучей на
max
Интерференционные светофильтры
многолучевая интерференция
Слайд 50Дифракция света
Проявления дифракции:
волны заходят в область геометрической тени
Дифракция света
При условии
размеры
препятствий сравнимы с длиной волны
огибание световыми волнами препятствий
Виды дифракции
дифракция Френеля
в
расходящихся лучах
(сферических волн)дифракция Фраунгофера
в параллельных лучах
(∞ удаленный источник)
совокупность явлений, возникающих при прохождении света вблизи границ с резкими неоднородностями
лат. diffractus – разломанный, переломанный
дифракция выражена наиболее сильно
Слайд 51Объяснение явления дифракции
Дифракционные явления были хорошо известны
еще во времена
Ньютона
но объяснить их на основе корпускулярной теории света оказалось невозможным
Томас Юнг
Первое
качественное объяснение явления дифракцииОгюсте́н Жан Френе́ль
Количественная теория дифракционных явлений
на основе волновых представлений
Независимо
от Т.Юнга 1818 г.
В основе теории Френеля
принцип Гюйгенса, дополненный идеей об интерференции вторичных волн
принцип Гюйгенса-Френеля
Каждая точка волнового фронта является источником вторичных волн
Исаак Ньютон
(1642-1727
Англия)
Томас Юнг
(1773-1829
Англия)
Огюсте́н Жан Френе́ль
(1788-1827
Франция)
Христиан Гю́йгенс ван Зёйлихем
1629-1695
Нидерланды
Амплитуда и фаза волны в любой точке пространства – результат интерференции волн, излучаемых вторичными источниками
Все вторичные источники на поверхности фронта волны, когерентны между собой
Слайд 52Волновой принцип Гюйгенса
Каждая точка пространства, до которой доходит фронт волны,
становится точечным источником света,
излучающим сферическую волну
Огибающая
(новый
волновой фронт)
Вторичные
волныПервичный волновой фронт
явление дифракции объясняет лишь КАЧЕСТВЕННО
Огибающая всех вторичных волн представляет собой
фронт действительно распространяющейся волны
Слайд 53Дополнения Френеля к принципу Гюйгенса
Вторичные источники не точечные,
а элементы
фронта волны площадью dS
Вторичные источники dS – когерентные
и результат
их действия на точку Р
есть результат их интерференцииПлощадка фронта волны dS создает в точке P напряженность ЭП:
Принцип Гюйгенса-Френеля позволяет объяснить дифракцию КОЛИЧЕСТВЕННО и решить любую задачу на дифракцию света
dE ~ dS
dE ~ A0
A0 – амплитуда световой
волны в месте, где находится площадка
dE ~ α
α – угол между нормалью к площадке dS
и направлением на точку P
r – расстояние от площадки dS до точки P
dE ~ 1/r
Слайд 54Дифракция Френеля
Дифракция от круглого отверстия
Дифракция в расходящихся световых пучках,
когда дифракционная
картина наблюдается
на конечном расстоянии от препятствия
1.
Разобьем открытую часть волновой
поверхности
на зоны ФренеляГраницы зон
в плоскости отверстия
Слайд 55Результат действия зон Френеля
Действие зоны ↓ при ↑ угла между
к поверхности зоны и направлением
к точке наблюдения
Расстояния
от соседних
зон до точки наблюдения Р отличаются на λ/2~1 мм
открыты
все зоны Френеля
половине действия центральной зоны
Объяснение прямолинейности распространения света
оценка размера центральной зоны Френеля:
колебания от точек двух соседних зон приходят в т.P
в противофазе
A=А1-A2+A3-А4+A5-A6 …
A1>A2>A3>…>Аm
действие всей волновой поверхности
эквивалентно
Если
Слайд 56Результат действия зон Френеля
Количество открытых
зон Френеля
Амплитуда и интенсивность
в
центре дифракционной картины
одна
нечетное
четное
БОЛЬШЕ, чем при свободном распространении волны
A=0
свободный фронт
А0=½А1
Действие всей
волны –
половина действия первой зонытемное пятно
Амплитуда результирующего колебания
«+» m – нечетные
«-» m – четные
I=4I0
I0=¼I1
А=A1=2А0
I=4I0=0
выполняется условие min интерференции
m – нечетное
m – четное
две
I=0
А=A1-А2=0
выполняется условие max интерференции
А=6A0
I=36I0
Например,
открыты три зоны:1, 3, 5
Объяснение прямолинейности распространения света
Слайд 57Дифракция Френеля
Дифракция от диска
2.
пятно Пуассона (1818 г.)
дифракцией света можно пренебречь
и считать свет распространяющимся прямолинейно
в центре всегда наблюдается интерференционный max
(светлое пятно)первая открытая зона Френеля удаляется от центра и увеличивается угол т
D велик
А=½А1
D ↑
интенсивность центрального max ↓
за центральным max наблюдается тень, вблизи границ которой имеет место слабая дифракционная картина
D мал
D
Слайд 58Результат действия зон Френеля
Освещение белым светом
кольца окрашены
D велик
Аm
отверстия
интенсивность такая же,
как при полностью открытом волновом фронте
дифракционной картины
НЕТсвет распространяется прямолинейно
Немонохроматичность света
Интенсивность в max ↓
с расстоянием от центра
объяснение прямолинейности распространения света
Зонная пластинка
Использование
В рентгеновском диапазоне являются дифракционным аналогом обычных линз
и обладают наивысшим из рентгенооптических элементов пространственным разрешением.
Служат основным элементом в сканирующих
и изображающих рентгеновских микроскопах
с использованием синхротронного излучения.
действует подобно собирающей линзе –
линза Френеля
Слайд 59Дифракция на одной щели
в щели укладывается
НЕЧЕТНОЕ число зон Френеля
в
точке Р будет наблюдаться МАКСИМУМ
Если
в щели укладывается
ЧЕТНОЕ число зон
Френеляв точке Р будет наблюдаться МИНИМУМ
k=1, 2, 3, …
k=1, 2, 3, …
Слайд 60Дифракционная решетка
Уравнение главных МАКСИМУМОВ
Дифракционная решетка
Совокупность большого числа одинаковых щелей, расположенных
друг от друга
на одинаковом расстоянии
d – постоянная (или период)
дифракционной решеткиk=1, 2, 3, …
с ↑ числа щелей в дифракционной решетке:
амплитуды добавочных max ↓
угловая ширина центрального max ↓
Слайд 61Дифракционный спектр
Спектры, начиная со второго порядка, перекрываются
max
нулевого порядка
k=0
спектр
первого порядка
k=-1
спектр
второго
порядка
k=-2
спектр
второго порядка
k=2
спектр
первого порядка
k=1
спектр
третьего порядка
k=-3
спектр
третьего порядка
k=3
Слайд 62Дифракционная решетка
как спектральный прибор
Основные характеристики спектрального прибора
Дисперсия
определяет угловое или
линейное расстояние между двумя спектральными линиями
Угловая дисперсия численно равна углу
между двумя max одного порядка, отличающихся по λ на 1 метрЛинейная дисперсия численно равна расстоянию на экране между двумя max одного порядка, отличающихся по λ на 1 м
угловое расстояние между спектральными линиями, отличающимися по длине волны на dλ
…
порядок max
период решетки
линейное расстояние между соседними max одного порядка, отличающимися по длине волны на dλ
фокусное расстояние линзы
Слайд 63Разрешающая способность спектральных приборов
Разрешающая способность
определяет min разность
длин волн, при
которой
две линии воспринимаются
на спектре раздельно
Критерий Рэлея
две спектральные линии
считаются полностью разрешенными, если вершина одного max совпадает с основанием другогоРазрешающая сила спектрального прибора
Разрешающая сила дифракционной решетки
количество щелей
Слайд 64Дифракция рентгеновских лучей
Рентгеновское излучение
λ=0,0012…12 нм
1895 г., В.Рентген
Большая проникающая способность
λ сравнима
с d – периодом кристаллической решетки
Х-лучи
дифракция рентгеновских лучей в кристалле
λ
dвторичные волны
падающие рентгеновские лучи
период кристаллической решетки
формула
Вульфа-Брегга
угол скольжения лучей
m = 1, 2, 3,…
атомы крист.решетки – источники вторичных волн
Слайд 65 Применение дифракции рентгеновского излучения
зная λ
измеряя θ
вычисляется d
+
Рентгеноструктурный анализ
зная d
измеряя θ
вычисляется
λ
+
Рентгеновская спектроскопия
рентгеновское излучение
кристалл
экран
рентгеновское излучение
метод Лауэ – кристалл
метод Дебая-Шерера –
поликристаллСлайд 67В любой точке поля векторы
напряженности ЭП и МП перпендикулярны
и
лежат в плоскости,
вектору скорости
Естественный свет
Свет
суммарное электромагнитное излучение множества атомов
Световой
векторпредставляет собой
Естественный свет
направление распространения
волны рисунку
ЭМ волна – волна ПОПЕРЕЧНАЯ
для описания закономерностей поляризации света достаточно знать поведение лишь одного из векторов
при действии света на вещество основное значение
имеет ЭЛЕКТРИЧЕСКАЯ составляющая поля волны,
действующая на электроны в атомах вещества
Атомы излучают
световые волны независимо
друг от друга
световая волна, излучаемая источником, характеризуется равновероятными колебаниями светового вектора
свет с равновероятными ориентациями вектора Е
Плоскость колебаний
плоскость, в которой колеблется световой вектор
Слайд 68Поляризация света
Поляризация света
процесс ориентации вектора напряженности Е световой волны
в
определенном направлении
Поляризованный свет
свет, в котором направления колебаний светового вектора каким-либо
образом упорядоченыПлоско (линейно) поляризованный
световой вектор колеблется
в одной плоскости
Эллиптически поляризованный
результат наложения двух когерентных плоскополяризованных волн со взаимно плоскостями поляризации, в случае, когда конец вектора Е описывает эллипс
Поляризованный по кругу
конец вектора Е описывает окружность
Плоскость поляризации
плоскость колебания светового вектора Е
частный случай
Слайд 69Степень поляризации света
естественный свет
плоско поляризованный
частично поляризованный
Степень поляризации
Imax и Imin —
соответственно max
и min интенсивности частично поляризованного света, пропускаемого анализатором
Imax
= Imin Р = 0
Imin = 0
Р = 1
0 < Р < 1
Слайд 70Закон Малюса
Поляризатор
естественный свет
поляризованный свет
устройство для получения поляризованного света, пропускает колебания
Е только определенного направления
?
поляри-заторы
среды, анизотропные
в отношении колебаний Е,
напр.,
кристаллытурмалин
поляризатор
анализатор
I~ E2
закон Малюса
1810 г.
φ=0°
I =I’0
оси поляризатора и анализатора
φ=90°
I= 0
Закон Малюса
I0
I’0
I
Слайд 71Способы получения поляризованного света
Поляризация света при отражении и преломлении
на
границе двух диэлектриков
Фильтр повёрнут так,
что полностью
пропускает отражённый
от
поверхности светДве фотографии одного места, сделанные фотоаппаратом
с поляризующим фильтром, повёрнутым под разными углами
Фильтр повёрнут на 90°:
отражённый свет
почти полностью отфильтровывается
и блики исчезают
Слайд 72Закон Брюстера
1815 г.
Степень поляризации зависит от угла падения лучей
и показателя преломления
падающий неполяризованный свет
Степень поляризации преломленного света м.б. значительно
повышена многократным преломлением при условии падения света каждый раз на границу раздела под углом Брюстерастопа Столетова
отраженный плоскополяризованный содержит только колебания,
плоскости падения
преломленный поляризован максимально, но не полностью
n1
n2
Слайд 73Двойное лучепреломление
Все прозрачные кристаллы
двойного лучепреломления
?
обладают способностью
эффект расщепления
в анизотропных
средах луча света на две составляющие
оптическая анизотропия
кроме кристаллов кубической системы
Впервые
обнаружено на кристалле исландского шпата CaCO3 е
о
е – extraordinary необыкновенный
о – ordinary обыкновенный
1662 г.
призма Николя
Слайд 74Свойства обыкновенного
и необыкновенного лучей
Закон преломления:
для о-луча всегда выполняется
для е-луча
в общем случае не выполняется
1.
В кристаллах существует направление,
при распространении
вдоль которого двойного лучепреломления не происходит – оптическая ось, направление кристалла2.
О
О’
Плоскость, проходящая через световой луч
и оптическую ось кристалла –
главная оптическая ось или плоскость главного сечения
3.
о-луч и е-луч поляризованы во взаимно плоскостях
плоскость поляризации о-луча плоскости главного сечения
4.
Слайд 75Искусственная анизотропия при деформации. Фотоупругий эффект
прозрачные изотропные среды
механическая деформация
+
искусственная анизотропия
двойное
лучепреломление
П и А скрещены (φ=90°)
I = 0
напряжение
оптическая ось ОО’ по
направлению действия FМера оптической анизотропии
Фотоупругий эффект
возникновение оптической анизотропии в первоначально изотропных твёрдых телах
(в том числе полимерах) под действием механических напряжений
Фотоэластический
Пьезооптический
Д. Брюстер (1815)
Т.И. Зеебек (1813)
I 0
Слайд 76Воздействие электрического поля
1875
Использование эффекта Керра
для измерения скорости света
возникновение двойного лучепреломления
в жидкостях под действием электрического поля
Эффект Керра
Мера оптической анизотропии
время срабатывания
счетчика Керра τ ≈ 10-9cв качестве быстродействующего светового затвора
Слайд 77Воздействие магнитного поля
возникновение двойного лучепреломления в твердых телах под действием
МП
Эффект Фарадея
Мера оптической анизотропии
возникновение двойного лучепреломления в жидкостях под действием
магнитного поляЭффект Коттона-Мутона
Постоянная Верде
Слайд 78Воздействие магнитного поля
Итак,
мера оптической анизотропии
Искусственная оптическая анизотропия
возникает
под действием
одностороннего сжатия
(растяжения)
электрического поля
магнитного поля
название эффекта
фотоупругий, фотопластический
Керра
Фарадея
Коттона-Мутона
k1, k2, k3 – постоянные, характеризующие
веществоСлайд 79Вращение плоскости поляризации. Применение
При прохождении плоскополяризованного света через
некоторые вещества
наблюдается вращение плоскости поляризации
Оптические активные вещества (ОАВ)
Вещества, при прохождении через
которые плоскополяризованного света наблюдается поворот его плоскости поляризациикварц, скипидар, водный раствор сахара и др.
α – коэффициент пропорциональности, постоянная вращения
для растворов
для твердых веществ
С – концентрация вещества
Используется, например, для измерения концентрации вещества в растворе
Сахариметр
Слайд 80Применение
Создание различных оптических эффектов
В 3D-кинематографе
технология IMAX: линейная поляризация используется
для разделения
изображений,
предназначенных правому и левому глазу
в технологии RealD и MasterImage: подобна IMAX,
но
круговая поляризация позволяет сохранять стереоэффект и избегать двоения изображения
при небольших боковых наклонах головыВ антеннах космических линий связи (круговая поляризация):
для приёма сигнала не важно положение плоскости поляризации передающей и приёмной антенн, т.е. вращение космического аппарата не повлияет на возможность связи с ним
В наземных линиях: антенны линейной поляризации — всегда можно выбрать заранее — горизонтально или вертикально располагать плоскость поляризации антенн
Слайд 81Геометрическая оптика
в основе – представление о световых лучах,
как направлениях
переноса световой энергии
Слайд 82Геометрическая оптика
Геометрическая (лучевая) оптика
Раздел физики, в котором распространение света рассматривается
на основе представления о световых лучах, как направлениях переноса световой
энергииЛуч
геометрическая линия, вдоль которой переносится энергия электромагнитными волнами
Основное понятие геометрической оптики
Световой пучок,
исходящий из отверстия бесконечно малого размера
Направления, вдоль которых переносится световая энергия
Нормаль к фронту волны
распространение света в однородных средах и предметах, состоящих из однородных сред
<< х, где х – размеры оптических приборов
Область использования
Границы применимости законов геометрической оптики
Слайд 83Законы геометрической оптики
Прямолинейного распространения света
в оптически однородной среде
свет распространяется
прямолинейно
Независимости световых пучков
эффект, производимый отдельным пучком,
не зависит от действия
остальныхОтражения
падающий, отраженный
и преломленный лучи
и перпендикуляр
к границе раздела сред
в точке падения лежат
в одной плоскости
Преломления
Исследовательские задания
Закон Снелиуса
Слайд 84Исследовательское задание 1
Исследуйте зависимость угла преломления от угла падения
в
явлении преломления света на границе раздела двух сред
1.
Рассмотрите случаи с
разными соотношениями показателей
преломления двух оптических средОбоснуйте возникновение явления полного внутреннего отражения
Постройте ход лучей в поворотных
и оборотных призмах и перископе
Рассмотрите случай падения на границу раздела двух сред широкого пучка параллельных световых лучей
Рассмотрите и объясните
принцип действия рефрактометра
a)
b)
c)
e)
f)
α
β
γ
n1
n2
Рассмотрите случай падения на границу раздела двух сред пучка световых лучей от точечного источника света
d)
Слайд 85Исследовательское задание 2
Исследуйте явление прохождения светового луча
через плоскопараллельную пластинку
2.
Найдите
зависимость бокового смещения падающего луча
от угла падения
a)
b)
α
β
γ
Рассмотрите случаи
различного соотношения показателей преломления плоскопараллельной пластинки и среды, в которой находится пластинка α
d
n1
n2
n3
Рассмотрите случай падения
на пластинку широкого пучка параллельных лучей
с)
Рассмотрите случай освещения пластинки рассеянным светом
d)
Рассмотрите случай падения пучка световых лучей от точечного источника света
e)
При изучении интерференции
в тонких пленках
Слайд 86Исследовательское задание 3
Исследуйте явление прохождения светового луча
через клинообразную пластинку
(тонкую призму)
3.
Выведите формулу и найдите зависимость угла смещения светового
луча от угла падения
и соотношения показателей преломления среды и пластинкиa)
b)
Какие эффекты будут наблюдаться при прохождении кварцевой клинообразной пластинки линейно поляризованного света?
Рассмотрите случаи падения
на клин широкого пучка параллельных световых лучей
и освещение клинообразной пластинки рассеянным светом
с)
A
1
2
1
2
n1
n2
A
n3
При изучении дисперсии
Слайд 87Полное внутреннее отражение
При переходе света из оптически более плотной среды
в оптически менее плотную n2
при углах падения α > α пр – угол полного внутреннего отраженияволоконный световод
Полное внутреннее отражение
Использование световода
Слайд 89Сферические зеркала
O – оптический центр
P – полюс
F – главный (мнимый)
фокус зеркала
OP – главная оптическая ось
R – радиус кривизны зеркала
f
– расстояние до изображенияd – расстояние до предмета
Исследовательские задания
Слайд 90Исследовательские задания
Исследуйте,
как будут меняться параметры изображения, если предмет удалять
от вершины ВЫПУКЛОГО сферического зеркала
в бесконечность?
Исследуйте,
как будут меняться
параметры изображения, если предмет удалять
от вершины ВОГНУТОГО сферического зеркала
в бесконечность?Отражение параллельного пучка лучей
от вогнутого (1) и выпуклого (2) сферического зеркала
Слайд 91Тонкие линзы
Собирающие (a)
и рассеивающие (b) линзы
и их условные обозначения
Преломление параллельного
пучка лучей в собирающей (a) и рассеивающей (b) линзах
O1 и O2 –
центры сферических поверхностейO1O2 – главная оптическая ось
O – оптический центр
F – главный фокус
F‘ – побочный фокус
OF‘ – побочная оптическая ось
Ф – фокальная плоскость
Слайд 92Тонкие линзы
Построение изображения в СОБИРАЮЩЕЙ линзе
Исследовательское задание:
Исследуйте, как будут меняться
параметры изображения, если предмет удалять от СОБИРАЮЩЕЙ линзы
в бесконечность?
Слайд 94Тонкие линзы
Построение изображения в РАССЕИВАЮЩЕЙ линзе
Исследовательское задание:
Исследуйте, как будут меняться
параметры изображения, если предмет удалять от РАССЕИВАЮЩЕЙ линзы
в бесконечность?
Слайд 96Глаз, как оптическая система
1 – склерой
2 – роговица
3 – радужная
оболочка со зрачком (от 2 до 8 мм, т.е. действует
подобно диафрагме фотоаппарата)4 – хрусталик
5 – мышца, изменяющая в некоторых пределах форму хрусталика, изменяя тем самым его оптическую силу
Остальная часть глаза заполнена стекловидным телом
6 – глазное дно 7 – палочки и колбочки, являющиеся светочувствительными элементами
Дефекты зрения и их коррекция
дальнозоркость
близорукость
Слайд 97Оптические приборы
Лупа
Микроскоп
Телескоп
коэффициент увеличения
предмет – между фокусом и линзой
Слайд 99Аберрации оптических систем
Сферическая аберрация
Проявляется при отображении точек,
лежащих на оптической
оси системы
Лучи, проходящие через края линзы, преломляются сильнее лучей,
проходящих
вблизи оптической осиПерераспределение освещенности
в изображении светящейся точки
Аберрация – от лат. aberratio «уклонение, удаление, отвлечение» – отклонение от нормы, ошибка, погрешность
Применение оптических стёкол с высокими n позволяют ↓ сферическую аберрацию, посредством ↑ радиусов поверхностей линзы при сохранении её оптической силы
Диафрагмирование
Дефокусировка
Применение нескольких линз
Может быть исправлена только для узких зон
Исправление
Снижение резкости изображения
Слайд 100Аберрации оптических систем
Хроматическая аберрация
Для разных λ возникают различные изображения на
разном расстоянии от линзы
постороннее окрашивание изображения
снижение чёткости изображения
Ахроматические линзы
Исправление
обусловлена дисперсией
оптических сред: свет разной λ преломляется по-разномуСлайд 101Аберрации оптических систем
изображение точки, расположенной близко к оптической оси, мало
отклоняется от своего идеального положения
изображение точки предмета,
далекой от оптической
оси, смещено
от идеального положения тем больше, чем дальше от оси находится эта точкаподушкообразная дисторсия
различие линейного увеличения для точек предмета, находящихся на разных расстояниях от главной оптической оси
нарушение геометрического подобия между предметом и его изображением
при больших углах падения лучей на линзу
бочкообразная дисторсия
Дисторсия
Слайд 102Аберрации оптических систем
Кома
При прохождении широкого пучка, не параллельного оптической оси
изображение
источника в виде освещенного пятнышка, напоминающего кометный хвост
Устранение комы –
так же, как сферической аберрацииАстигматизм
обусловлен неодинаковостью кривизны линзы в разных плоскостях сечения падающего на нее светового пучка
Исправляется с помощью цилиндрических линз
Одновременное исправление всех погрешностей – задача крайне сложная, а иногда неразрешимая
При прохождении через оптическую систему внеосевого узкого светового пучка его лучи испытывают неодинаковое преломление
в различных плоскостях
кривизна фронта световой волны
в разных плоскостях преломления различна
изображение точки предмета
в разных плоскостях также получаются в различных местах
!
Слайд 104Взаимодействие света с веществом
?
вещество
Зависимость скорости распространения световых волн
от длины
волны
Дисперсия
Поглощение
Рассеяние
Рассеяние света
на пространственных неоднородностях
в оптически неоднородной среде
Уменьшение энергии световой
волны, проходящей через вещество за счет
ее превращения во внутреннюю энергиюНесобственное свечение вещества
h
Какие явления наблюдаются
при взаимодействии света с веществом?
Слайд 105Дисперсия света
Детальные экспериментальные наблюдения дисперсии света – И.Ньютон (1672 г.)
К
чему это приводит?
Разложение
белого света в спектр
Слайд 106Дисперсия света в призме
1
угол отклонения лучей призмой тем больше, чем
больше преломляющий угол призмы
или:
А↑
↑
=f(n)
n=f()
но:
лучи разных длин волн после прохождения призмы
отклоняются на разные углы2
=f()
разложение белого света
в спектр
=f(А)
т.е:
A
1
2
1
2
n1
n2
A
n1
=const
А – преломляющий угол призмы
ϕ – угол отклонения лучей
Слайд 108Схема образования радуги
сферическая капля
входящий луч света
преломление
полное внутреннее отражение
первичная радуга
вторичная радуга
наблюдатель
область
формирования
первичной радуги
область формирования
вторичной радуги
облако капелек
Угловой радиус радуги:
первичной – 40-42°
вторичной
– 50-53°2
4
3
Первичная радуга:
Вторичная радуга:
2
3
3
3
4
4
5
6
7
8
9
10
Слайд 109Радуга
Схема образования радуги:
сферическая капля
внутреннее отражение
первичная радуга
преломление
вторичная радуга
входящий луч света
ход лучей
при формировании первичной радуги
ход лучей при формировании вторичной радуги
наблюдатель
область формирования
первичной
радугиобласть формирования вторичной радуги
облако капелек
Угловой радиус радуги:
первичной – 40-42°
вторичной – 50-53°
1
2
1
Слайд 110Дифракционный
и дисперсионный спектры
Разлагая свет в спектр с помощью призмы или
с помощью дифракционной решетки
Дифракционный спектр
Дисперсионный спектр
разложение
по длинам волн
измерить
определить
разложение
по значениям nдифракционная решетка
призма
?
можно определить его спектральный состав
Спектральный анализ
надо знать
2.
1.
Расположение составных цветов в спектрах
кр > ф
sin
красные лучи отклоняются
дифракционной решеткой сильнее
↑
n↓
т.к:
красные лучи отклоняются
призмой меньше
?
?
Слайд 111Применение дисперсии
Призменные спектрографы
Нормальная дисперсия
необходимость градуировки
различная дисперсия
в разных участках спектра
Определение спектрального состава света
Спектральный анализ
Достоинства
изготовление хороших призм значительно проще,
чем изготовление
хороших дифракционных решетокНедостатки
в призменных спектрографах легче получить большую светосилу
Слайд 112Объяснение явления дисперсии света
Теория Максвелла
В оптической области спектра для всех
веществ 1
противоречие с опытом
Теория Максвелла
НЕ объясняет явление дисперсии
n –
величина переменная?
n – величина постоянная
численные значения n – теоретические и опытные различаются
2.
1.
!
Теория Лоренца
Дисперсия света
результат взаимодействия ЭМ волн
с электронами атома, совершающими вынужденные колебания
в переменном ЭМ поле волны
Слайд 113Качественное объяснение дисперсии
е- в атоме диэлектрика под действием ЭМ волны
совершает
вынужденные колебания с частотой ν
переизлучает вторичные ЭМ волны той
же частотызависит
от частоты света ν
объяснение
зависимости скорости ЭМ волны от её частоты
время
распространения волны
Время
возбуждения атома
Время
переизлучения ЭМ волны
Слайд 114Количественное объяснение дисперсии
Под действием ЭМ волны происходит смещение е- на
расстояние z между центрами «+» и «-» зарядов
F возбуждающая
F возвращающая
F
тормозящая на е- действуют силы:
n>1
нормальная дисперсия
поглощение ЭМ волн
без учета сил сопротивления при колебаниях электронов
с учетом сил сопротивления
при колебаниях электронов
аномальная дисперсия
область I:
нормальная дисперсия
область II:
n → ∞
0 ≤ ω ≤ ω0
ω → ω0
область III:
n>1
0 ≤ ω ≤ ω0
Слайд 115Дисперсия вещества
физическая величина, показывающая,
как быстро изменяется показатель преломления с длиной
волны
Дисперсия вещества
Для прозрачных веществ
Нормальная дисперсия
НО!
вблизи линий и полос поглощения:
n увеличивается
с увеличением Аномальная дисперсия
!
Слайд 116Поглощение (абсорбция) света
Поглощение (абсорбция) света
явление уменьшения энергии световой волны при
ее распространении
в веществе
?
вещество
явление ↓ интенсивности света, проходящего через вещество
за счет ↑ его внутренней энергииили
I0
hν
I
hν
l
I < I0
поглощение
I = I0
отсутствие поглощения
I > I0
работают оптические квантовые генераторы (лазеры)
Объяснение с т.з. волновой и квантовой природы света
Энергия ЭМ волны → в энергию е-
Часть энергии ЭМ волны предается ионам
и кристаллической решетке
hν ↓,
энергия е- ↑
↓ интенсивности света, проходящего через вещество
нагрев кристалла
Слайд 117Закономерности поглощения света
— коэффициент поглощения
Закон
Бугера-Ламберта
I0
hν
I
hν
x
dx
Закон поглощения
в дифференциальной
форме
численно равен относительному уменьшению интенсивности излучения при прохождении слоя диэлектрика
толщиной
в единицу длиныинтегрируя:
Поглощение происходит вблизи собственных резонансных частот колебаний е-
Вещество поглощает ЭМ излучение только лишь на определенных (дискретных) частотах
Излучать данный диэлектрик может только на этих частотах
При х=1/ интенсивность света I по сравнению с I0 уменьшается в е раз
физический смысл
Слайд 118Коэффициент поглощения
зависит от:
интенсивности света (для малых значений)
длины волны
химической
природы
состояния вещества
НЕ зависит от:
Типичные зависимости от
и n
от в области полосы поглощенияполоса поглощения
аномальная дисперсия
Для больших значений интенсивности
явление открыто Вавиловым в 30-е гг. XX века, положило начало возникновению нелинейной оптики
большее количество е- будет находиться в возбужденном состоянии
фотоны поглощаться не будут
α будет уменьшаться при дальнейшем ↑ I
окрашенности поглощающих тел
разнообразие
и богатство цветов
и красок в окружающем мире
Разнообразие пределов избирательного поглощения
у различных веществ
объяснение
Слайд 119Применение явления поглощения
стекло, слабо поглощающее красные
и оранжевые лучи и
сильно поглощающее зеленые и синие, при освещении белым светом будет
казаться краснымСветофильтры
в зависимости от химического состава фильтры пропускают свет только определенных длин волн, поглощая остальные
Абсорбционный спектральный анализ
измерение частот и интенсивностей линий (полос)
в спектре поглощения
Слайд 120Виды спектров
Спектр поглощения
нагреватель
экран
hν
вещество
экран
вещество
совокупность частот (длин волн),
поглощаемых (излучаемых) данным веществом
Спектр
Спектр
излучения
hν
Q
Слайд 122Виды спектров
одноатомные газы
и пары металлов
10–12-10–11 м-1
Коэффициент поглощения α
колебания атомов
в молекулах
сложные газы, молекулы
Линейчатый
собственные колебания электронов
в атомах
Селективное поглощение (излучение)
света
в определенных интервалах длин волн, когда резко ↑,
и наблюдаются сравнительно широкие спектральные полосыРезкие max для очень узких спектральных областей
нет свободных е-
явление резонанса
при вынужденных колебаниях
электронов в атомах
и атомов в молекулах диэлектрика
Вещество
Чем обусловлен
Вид спектра
10–10-10–7 м-1
Полосатый
диэлектрики твердые и жидкие тела, вещества, находящиеся
в конденси-рованном состоянии
10–5- 10–3 см-1
Сплошной
металлы
103- 105 см-1
непрозрачны для света
объяснение - ?
Слайд 125Спектральный анализ
Физические методы определения состава вещества,
основанные на получении и
исследовании его спектров
КАЧЕСТВЕННЫЙ
спектральный анализ
КОЛИЧЕСТВЕННЫЙ
спектральный анализ
Анализ химического состава вещества
по его спектру
(без определения концентраций)Определение концентрации веществ в смесях по их спектрам поглощения и излучения
КАКИЕ
химические элементы?
Сравнение интенсивности линий искомого вещества
с интенсивностью линий стандартного вещества
Сопоставление с известными спектрами химических элементов
Какова КОНЦЕНТРАЦИЯ элементов?
Структура спектров определяется составом
и строением молекул
изучение спектров поглощения –
один из основных методов исследования веществ
Слайд 126Излучение Вавилова-Черенкова
Свечение сиреневатого оттенка, возникающее в результате прохождения через вещество
заряженных частиц со скоростями большими, чем фазовая скорость световой волны
в этой средезаряженная частица, попадая в т.А, вызывает поляризацию среды
Смещение электрических зарядов за счет поляризации
и деполяризации среды
в т.В снова происходит поляризация среды другими молекулами
в т.А среда возвращается к исходному равновесному состоянию
источник излучения Вавилова–Черенкова
Слайд 127Рассеяние света
Рассеяние света
несобственное свечение вещества
при прохождении через него света
Рассеяние
и поглощение света приводит к ↓ I света, проходящего через
веществоОднако,
при рассеянии
энергия НЕ идет на ↑ внутренней энергии вещества
Если в веществе наблюдается
и поглощение,
и рассеяние, то:
α1 – коэф. поглощения
α2 – коэф. рассеяния
Слайд 128Рассеяние света
Рассеяние происходит в резко неоднородных (мутных) средах
Виды рассеяния
Рассеяние Тиндаля
Рассеяние,
обусловленное дифракционными эффектами
Рассеяние, обусловленное законами геометрической оптики
светящийся конус на тёмном
фоне – так называемый конус ТиндаляВиды мутных сред
Дым
взвесь твердых частичек в воздухе
Туман
взвесь капелек жидкости в воздухе
Суспензия
взвесь твердых частичек в жидкости
Эмульсия
взвесь капелек одной жидкости в другой
max поляризация при θ < π/2
Зависимость интенсивности рассеянного света от угла
В общем случае рассеянный свет оказывается поляризованным
Слайд 129Молекулярное рассеяние света
Молекулярное рассеяние света
Рассеяние света чистыми жидкостями и газами
рассеяние
света в чистых жидкостях
и газах происходит на флуктуациях плотности
1908
г. гипотеза Смолуховского:Флуктуации плотности
Среда является оптически неоднородной
Флуктуации показателя преломления n
вызывает появление
Слайд 130Цвета тел
Для того чтобы возникло ощущение цвета необходимо
ЭМ излучение, попадающее
в глаз человека
глаз, регистрирующий световую энергию
система передачи информации
по нервным
волокнам из глаз в мозгналичие мозга, который формирует изображение
Цвет – есть нечто субъективное,
не существующее без человека
Все тела в природе делятся на:
светят отраженным светом
несамосветящиеся
самосветящиеся
цвет тел обусловлен
цвет обусловлен спектральным составом
излучения
спектральным составом излучения, падающего на тело
поглощательной (отражательной) способностью тела
Слайд 132Скорость света.
Методы измерения скорости света
Скорость света в вакууме –мировая физическая
константа
299 792 456,21,1 м/с
3·108 м/с
Экспериментальные измерения, 1972 г. Ивенсон, США
Группы
методов измерения света Лабораторные
Астрономические
Современные
Метод Ремера, 1676
Метод Брадлея. Аберрация света, 1727
Метод зубчатого колеса
(метод Физо)
Метод ячеек Керра
Метод световой или радиолокации
Метод объемного резонатора
Метод Ивенсона
Слайд 133Астрономические методы измерения скорости света
Основа метода
Метод Ремера, 1676
Наблюдение затмений крупнейшего
спутника Юпитера Ио
Метод Брадлея. Аберрация света , 1727
Наблюдение кажущегося смещения
звезд
на небесном своде - аберрация светаОснова метода
Слайд 134Лабораторные методы измерения скорости света
Метод зубчатого колеса (метод Физо)
Метод ячеек
Керра
Слайд 135Лабораторные методы измерения скорости света
Метод световой или радиолокации
Метод объемного резонатора
В
объемном резонаторе возбуждают стоячие ЭМ волны, измеряются резонансные частоты. Скорость
ЭМ волн входит в уравнение, связывающее их с геометрическими параметрами резонатораМетод Ивенсона
Первый способ измерения фазовой скорости света
с большой точностью измерялась интерференционными методами
- методом деления частоты
Слайд 137Эффект Доплера
Продольный эффект Доплера
Поперечный
эффект Доплера
Эффект Доплера
для ЭМ волн
в
вакууме
0 – излучаемая частота
– частота, воспринимаемая приемником
– скорость
источника относительно приемника, – угол между вектором и направлением наблюдения, - система отсчета связана с наблюдателем
Изменение частоты волны, воспринимаемой приемником при движении источника
и приемника относительно друг друга
для волн различной природы
(гудок поезда)
при = 0
наблюдение вдоль распространения волн
при = /2
наблюдение в направлении перпендикулярном распространению волн
при << c
при > 0
<0, >0
сдвиг в более длинноволновую область
Красное смещение
удаление
при < 0
>0, <0
сдвиг в более коротковолновую область
Фиолетовое смещение
сближение
обнаружение поперечного эффекта Доплера связано
с большими трудностями
не наблюдается в акустике
релятивистский эффект
связан с замедлением течения времени движущегося наблюдателя
Обнаружен в 1938 г. в опытах американского физика Г. Айвса
Обнаружен в 1900 г. русским астрофизиком А. А. Белопольским
Слайд 138Экспериментальная проверка эффекта Доплера
эффекта Доплера НЕТ
эффекта Доплера ЕСТЬ
Выполнимость эффекта Доплера
проверена в 1907 г. в опытах Белопольского:
Со скоростью перемещался
мнимый источник светаСмещение – в сторону красной части спектра
Опыты Белопольского подтвердили справедливость эффекта Доплера с погрешностью ≈ 20%
Слайд 139Значение и применение эффекта Доплера
Радиолокация
Для измерения скорости приближающихся или удаляющихся
объектов
Радиоастрономия
Для определения лучевой скорости звезд
Существует так называемое красное смещение в
спектрах излучения звезд.Большинство звезд, которые можно различить в телескоп, удаляясь, смещают свой спектр в сторону красного спектра
Для определения естественной ширины спектральных линий
Естественная ширина спектральных линий обусловлена скоростью теплового движения атомов и молекул
Слайд 140Абсо́рбция (лат. absorptio ← absorbere — «поглощать») — явление поглощения
сорбата всем объёмом сорбента
Сорбция
Адсорбция (лат. ad — на, при; sorbeo
— поглощаю) — процесс сгущения газообразного
или растворенного вещества
на поверхности раздела фазПроцесс, обратный адсорбции, то есть перенос вещества с поверхности раздела фаз в объём фазы, называется десорбция
физическое сцепление ионов
и молекул на поверхности тела другого состояния
(напр., реагенты адсорбируются к целой поверхности катализатора)
Адсорбция
Абсорбция
объёмное слияние двух веществ, находящихся в разных агрегатных состояниях
(напр., жидкости, абсорбирующиеся твёрдыми телами или газами, газы, абсорбирующиеся жидкостями и т.д.)
Слайд 142Фотоэффект
Вырывание электронов из металлов
под действием света
металлическая пластинка
q = 0
Фотоэффект
Впервые наблюдал
явление фотоэффекта
Генрих Герц
металлическая пластинка
q > 0
УФ свет
1888 г.
Столетов
создание первого
фотоэлементаприменение фотоэлемента на практике
установление прямой зависимости силы фототока от интенсивности падающего света
1899 г.
Дж.Дж. Томпсон и Ф. Ленард
доказали, что при фотоэффекте свет выбивает из вещества электроны
Слайд 143Виды фотоэффекта
вырывание электронов из металла, под действием света
Внешний фотоэффект
увеличение проводимости
вещества под действием света
Внутренний фотоэффект
возникновение фото ЭДС
под действием света
Вентильный
фотоэффектh
е-
h
↑
h
↑
Фотоэлектронная эмиссия
выход электронов
за пределы металла
↑ концентрации свободных электронов
фотоэффект
в запирающем слое
частный случай внутреннего фотоэффекта
металл
полупроводник
p-n переход
Слайд 144Законы фотоэффекта
Максимальная кинетическая энергия вырываемых светом электронов линейно возрастает с
частотой света и НЕ зависит от его интенсивности
1-й закон (закон
Столетова) Фототок насыщения прямо пропорционален световому потоку
для каждого вещества существует красная граница фотоэффекта, т.е. минимальная частота света 0
(или максимальная длина волны), при которой ещё возможен фотоэффект,
и если 0 < 0, то фотоэффект уже не происходит
2-й закон
3-й закон
Количество фотоэлектронов, выбиваемых
из катода за 1 с, прямо пропорционально интенсивности излучения
или
Слайд 145Уравнение Эйнштейна
для внешнего фотоэффекта
Энергия фотона расходуется на ионизацию атома
вещества и на работу, необходимую для «вырывания» электрона, а остаток
переходит в кинетическую энергию электрона1905 г.
А.Эйнштейн
Нобелевская премия 1921 г.
«За заслуги перед теоретической физикой
и особенно за объяснение закона фотоэлектрического эффекта»
Закон сохранения энергии для фотоэффекта
Слайд 146Законы фотоэффекта
Уравнение Эйнштейна
для фотоэффекта
Максимальная кинетическая энергия вырываемых светом электронов линейно
возрастает с частотой света и
НЕ зависит от его интенсивности
1-й
закон (закон Столетова) Фототок насыщения прямо пропорционален световому потоку
для каждого вещества существует красная граница фотоэффекта, т.е. минимальная частота света 0
(или максимальная длина волны), при которой ещё возможен фотоэффект,
и если < кр, то фотоэффект уже не происходит
2-й закон
3-й закон
Количество фотоэлектронов, выбиваемых
из катода за 1 с, прямо пропорционально интенсивности излучения
Слайд 147Объяснение явления
Силы, возвращающие электроны вглубь металла:
1.
притяжение к + ионам
2.
отталкивание от е-, находящихся в наружном электронном слое
Часть падающего ЭМ
излучения
от поверхности металла отражаетсяЧасть проникает внутрь поверхностного слоя металла
и там поглощается
Поглотив фотон, электрон получает от него энергию и, совершая работу выхода, покидает металл
Слайд 148Вольтамперная характеристика
Напряжение, при котором анодный ток прекращается
ток насыщения
В результате хаотического
теплового движения некоторые е- достигают А
Ток насыщения – все е-
под действием приложенного U достигают анода I0 при U=0
I2
I1
Максимальная кинетическая энергия, которую может иметь электрон при вылете из металла
Слайд 149Схема опыта
Поглотив фотон, электрон получает
от него энергию и,
совершая
работу выхода,
покидает металл
Максимальная кинетическая энергия, которую может иметь электрон
при вылете из металлаНапряжение, при котором анодный ток прекращается
Слайд 150Практическое применение фотоэффекта
Фотоэлементы разных типов
Вакуумные фотоэлементы
Газонаполненные фотоэлементы
газ при низком
давлении увеличивает силу тока за счет ударной ионизации
Фотосопротивления
Вентильные элементы –
солнечные батареи (=10…20%)С.И.Вавилов:
в области наибольшей чувствительности (λ=555 нм)
глаз начинает реагировать на свет при попадании
на зрачок примерно 100 фотонов в секунду
Слайд 152Давление света
давление, производимое светом
на отражающие и поглощающие тела,
частицы,
отдельные молекулы и атомы
Давление света
Впервые гипотеза светового давления
И.Кеплер для объяснения
отклонения хвоста комет,
пролетающих вблизи Солнца1899 г. – П.Н.Лебедев
первые опыты по исследованию светового давления
Крутильные весы
Вакуумированный сосуд
Тонкие диски из слюды
и различных металлов
на тонкой проволоке
Попеременное облучение разных сторон крылышек – нивелирование радиометрических сил
Удовлетворительное (±20%) совпадение
с теорией Максвелла
Одно из явлений, подтверждающих теорию Максвелла
Слайд 153Объяснение давления света
Давление света можно объяснить как с точки зрения
электромагнитной так и фотонной теории
!
заряды приходят в движение
с т.з. электромагнитной
теорииСо стороны ЭМ волны на заряды действуют силы F+ и F-
заряды вдавливаются
в вещество
На движущиеся заряды действует сила Лоренца
Сила, создающая давление света
Слайд 154Объяснение давления света
Давление света можно объяснить как с точки зрения
электромагнитной так и фотонной тории
!
с т.з. фотонной теории
Фотон как частица
попадает на веществофотон передает веществу соответствующий импульс
Импульс, передаваемый ПОГЛОЩЕННЫМ фотоном
По II закону Ньютона
импульс силы
Импульс, передаваемый ОТРАЖЕННЫМ фотоном
…
Е – энергетическая освещенность
-коэффициент отражения
кол-во фотонов
Слайд 156Рентгеновское излучение
1895 г.
Свойства рентгеновского излучения
Большая проникающая способность –
свободно проходит
через ткани, дерево, металлы
Малая поглощательная способность – поглощается
в большей
степени тяжелыми металлами, например, свинцомФотохимическое действие – способно воздействовать на фотоэмульсии
Ионизирующая способность
Биологическая активность – губительно действует на живые клетки
Слайд 157Тормозное рентгеновское излучение
Тормозное рентгеновское излучение
По закону сохранения энергии
Т.е. существует max
частота излучения
тормозного рентгеновского излучения
ограничена в области
коротких длин
волн Вычисление постоянной Планка h
Тормозные излучение электронов высоких энергий отклоняющихся в электрическом поле атомного ядра
Энергия ускоренного электрона передается аноду или в виде тепла,
или излучается в виде кванта тормозного рентгеновского излучения
возникает в результате торможения е- анодом
имеет сплошной спектр
Слайд 158Характеристическое рентгеновское излучение
возникает при достаточно больших U на аноде
характеризует материал
анода
имеет линейчатый спектр
Линии характеристического рентгеновского излучения
Обычно характеристическое и тормозное излучения
существуют одновременноСлайд 159Возникновение характеристического излучения
Объяснение возникновения характеристического излучения
по теории Бора
Внешний ускоренный е-
выбивает электрон е-
с одной из внутренних электронных оболочек атома
на
каждом энергетическом уровне
z=2n2 электроновизлучается линия
излучается линия
излучается линия
в общем случае длина волны характеристического излучения
z – заряд ядра
m – номер оболочки,
НА которую переходит е-
n – … С которой…
– постоянная экранирования (серии)
R=1,097∙107 м-1 – постоянная Ридберга
закон Мозли (1913)
определение заряда химического элемента
совпадение с порядковым номером
по табл. Д.И.Менделеева
Характеристическое излучение возникает при переходе вышележащих электронов на освободившееся место
n – номер энергетического уровня
Слайд 161Эффект Комптона
не зависит от природы рассеивающего вещества
1923 г.
В рассеянных лучах,
наряду с излучением первоначальной длины волны λ, содержатся лучи большей
длины волны λ’λк=2,426∙10-12 м
комптоновская длина волны
Объяснение по фотонной теории
закон сохранения импульса
закон сохранения энергии
=
?
h
е-
Слайд 163Эффект Комптона
Значение комптоновского эффекта
подтверждает квантовую фотонную природу рентгеновского излучения
подтверждает применимость
законов сохранения
в микромире
Исследовательские задания:
Опишите на основе методологии научного исследования
работы Комптона по рассеянию рентгеновского изучения на свободных электронахИсследуйте зависимость длины волны и интенсивности рассеянного излучения от угла рассеяния
Слайд 165Тепловое излучение
Излучение тел, вызванное их нагреванием
Тепловое излучение
Ускоренно движущиеся заряженные частицы
Источник
излучения
Свечение тел, вызванное ВНЕШНИМ воздействием
Люминес-ценция
Следует отличать тепловое излучение от люминесценции
!
Существует
при любой температурепри низких Т – длинноволновые (ИК) ЭМ волны
при высоких Т– короткие (УФ) ЭМ волны
Может находиться в равновесии
с излучаемым его телом
Существует, пока есть внешнее воздействие
Тепловое равновесие
тело излучает
температура тела ↓
Слайд 166Характеристики теплового излучения
физическая величина, численно равная энергии излучения с единицы
поверхности за единицу времени
в единичном интервале частот
Спектральная плотность энергетической
светимостиэнергия излучения с единицы поверхности за единицу времени
в интервале частот от 0 до ∞
Энергетическая светимость
отношение поглощенной энергии
к той энергии, которая подходит
к данной поверхности
Поглощательная способность
Слайд 167Абсолютно черное тело
Тело, обладающее свойством поглощать все падающее
на его
поверхность ЭМ излучение любого спектрального состава
Абсолютно черное тело (АЧТ)
идеализация, модель
!
Вход
в пещеруСажа
Черный бархат
примеры:
Окно извне
Торец трубы
Отверстие в замкнутой полости
спектральная плотность энергетической светимости АЧТ
энергетическая светимость АЧТ
поглощательная способность АЧТ
Слайд 168Закон Кирхгофа
НЕ зависит от природы тела
Отношение спектральной плотности энергетической светимости
любого тела к его поглощательной способности есть величина, равная спектральной
плотности энергетической светимости АЧТ (функция Кирхгофа)!
Энергия излучения
с единицы поверхности
за единицу времени
в единичном интервале частот
Спектральная плотность энергетической светимости
Отношение поглощенной энергии к той энергии, которая подводится
к данной поверхности
Поглощательная способность
функция Кирхгофа
является для всех тел одной и той же функцией частоты (длины волны) и температуры
Слайд 169Следствия из закона Кирхгофа
1.
излучение
поглощение
Максимальной спектральной плотностью энергетической светимости обладает абсолютно
черное тело Аν,Т=1
Если при какой-либо температуре тело не поглощает энергию,
то оно при этой температуре и не излучает Аν,Т=02.
Слайд 170Законы теплового излучения
1879 – эксперимент – Стефан
1884 – теоретическое обоснование
– Больцман
Энергетическая светимость АЧТ численно равна энергии излучения с единицы
поверхности за единицу времениСпектральная плотность энергетической светимости пропорциональна температуре в 4 степени
энергия излучения
с площади S за время t
постоянная Стефана-Больцмана
1893 – Вин впервые установил вид функции Кирхгофа
некоторая неизвестная Вину функция
Закон Вина
Закон
Стефана-Больцмана
Слайд 171Закон смещения Вина
При повышении температуры , соответствующая максимуму спектральной плотности
энергетической светимости смещается в сторону коротких длин волн
Закон смещения Вина
Из
закона ВинаСлайд 172Ультрафиолетовая катастрофа
Формула Рэлея-Джинса
Энергия,
излучаемая с 1 м2 за 1 с
Определение
функции Кирхгофа
Исходя из законов статистической физики
о равнораспределении
по степеням
свободыв единичном интервале частот
исходя из положений классической физики (5000 К)
по всем частотам
фактически
Энергия, излучаемая
с любой площади
НЕ может быть
∞ большой величиной
!
удовлетворительно описывает излучение только в области длинных волн
Возможно ли это?
Ультрафиолетовая катастрофа
Слайд 173Квантовая гипотеза
Макс Планк
Предложил согласующееся с опытными данными выражение для спектральной
плотности энергетической светимости черного тела
Квантовая гипотеза
атомы излучают энергию не непрерывно,
а определенными порциями — квантами, причем энергия кванта пропорциональна частоте колебанияh= 6,62510–34 Джс
постоянная Планка
Функция Кирхгофа
по Планку
1900 г.
!
Исследовательские задания:
Опишите на основе методологии научного исследования работы Планка
по изучению излучения абсолютно черного тела
Исследуйте зависимость спектральной плотности энергетической светимости
от частоты по формуле, полученной Планком на основе квантовой гипотезы
Слайд 174Законы теплового излучения
с точки зрения квантовой физики
Функция Кирхгофа
по Планку
Закон
Вина
Формула
Рэлея-Джинса
законы теплового излучения
Закон
смещения Вина
полагая
Закон
Стефана-Больцмана
Слайд 176Элементы квантовой физики
Представления о строении атома
Пространственная форма
s-, p-, d-,
f- атомных орбиталей
Слайд 177Элементы квантовой физики
Постулаты Бора
Существуют такие стационарные состояния атома, находясь
в
которых атом не излучает
и не поглощает энергии
1.
При переходе из
состояния
с большей энергией (удаленной от ядра орбиты) в состояние с меньшей энергией (ближе к ядру) происходит излучение энергии2.
Слайд 178Элементы квантовой физики
Волновые свойства частиц
Волновые свойства присущи ВСЕМ частицам
универсальное, общее
свойство материи
формула
де Бройля
Частице m=1 г, движущейся со υ=1 м/с,
соответствует
волна де Бройля с = 6,6210–31 мТакая длина волны лежит за пределами доступной наблюдению области
Волновые свойства должны быть присущи и макроскопическим телам
!
?
Почему они
не обнаруживаются экспериментально?
считается, что макроскопические тела проявляют только одну сторону своих свойств — корпускулярную — и не проявляют волновую
Слайд 179Соотношение неопределенностей Гейзенберга
Двойственная корпускулярно-волновая природа частиц вещества
нельзя говорить
Ограничение применения понятий
классической механики
к объектам микромира
По законам классической механики частица движется
по определенной траекториив любой
момент времени
координата х
и импульс р
точно определены
об одновременном определении точных значений х и р
о движении микрочастицы
по определенной траектории
1927 г.
невозможно одновременно
точно определить координату частицы и ее импульс
чем точнее определена координата, тем > неопределенность импульса
x → 0
p → ∞
!
Соотношения неопределенностей Гейзенберга
Е – неопределенность энергии некоторого стационарного состояния системы
t – промежуток времени, в течение которого существует данное состояние системы
x → ∞
p → 0
Слайд 180Особенности квантовой теории
Экспериментальное подтверждение идеи де Бройля об универсальности корпускулярно-волнового
дуализма
развитие
квантовой теории
Ограниченность применения классической механики
к микрообъектам
(соотношение неопределенностей)
Противоречие ряда
экспериментов
с применяемыми в начале XX века теориямисоздание
квантовой механики
описывает законы движения
и взаимодействия микрочастиц с учетом их волновых свойств
Особенность квантовой теории
вероятностный подход к описанию состояния микрочастиц
состояние микрочастиц описывается –
с помощью волновой функции ψ(x,y,z),
являющейся основным носителем информации
об их корпускулярных и волновых свойствах
ψ-функция,
волновая функция
имеет смысл плотности вероятности,
т.е. определяет вероятность нахождения частицы в единичном объеме
в окрестности точки с координатами х, у, z
Слайд 181Волновая функция
Чтобы волновая функция являлась объективной характеристикой состояния микрочастиц, она
должна удовлетворять ряду условий
КОНЕЧНОЙ
(вероятность не м.б. >1)
ОДНОЗНАЧНОЙ
(вероятность не м.б.
неоднозначной
величиной)НЕПРЕРЫВНОЙ
(вероятность не может изменяться скачком)
-функция должна быть :
Волновая функция позволяет вычислять средние значения физических величин, характеризующих
данный микрообъект
ψ-функция,
волновая функция
имеет смысл плотности вероятности,
т.е. определяет вероятность нахождения частицы в единичном объеме
в окрестности точки с координатами х, у, z
напр., вероятность обнаружить частицу
в элементе dV
Слайд 182Уравнение Шрёдингера
1926 г.
Статистическое толкование
волн де Бройля
Соотношения неопределенностей Гейзенберга
уравнение движения
в квантовой механике, описывающее движение микрочастиц в различных силовых полях
– д.б. волновым, из него должны вытекать наблюдаемые на опыте волновые свойства частицОсновное уравнение нерелятивистской квантовой механики
Общее уравнение Шрёдингера (зависит от времени)
постоянная Планка
(с чертой)
оператор Лапласа (лапласиан)
i – мнимая единица
U(x,y,z,t) – потенциальная энергия частицы
в силовом поле, в котором она движется
ψ(x,y,z,t) – искомая волновая функция частицы
в силовом поле, в котором она движется
Слайд 183Уравнение Шрёдингера
для стационарных состояний
Стационарные состояния
состояния с фиксированными значениями энергии
т.е.
U(x,y,z,t) f(t)
НЕ зависит от времени
Это возможно, если силовое
поле,
в котором частица движется, стационарнорешение уравнения Шрёдингера –
в виде произведения двух функций:
функции т. КООРДИНАТ
функции т. ВРЕМЕНИ
Для многих физических явлений микромира уравнение Шрёдингера, зависящее от времени можно упростить, исключив (t)
зависимость от времени выражается множителем
после подстановки и преобразований
Е – полная энергия частицы
уравнение Шрёдингера для стационарных состояний
Слайд 184Применение уравнения Шрёдингера
уравнение Шрёдингера для
электрона в потенциальной яме
линейного гармонического
осциллятора
прохождения частицы через потенциальный барьер
электрон в атоме водорода
Линейный гармонический осциллятор
Решая
данное уравнение, получаемn = 1, 2, …
Совокупность уровней энергии
Слайд 185Электрон в одномерной потенциальной яме
Решая уравнение Шрёдингера, получаем:
U = 0
при 0 x l
U = ∞ при x
< 0 и х > l (0)= (l) = 0 при x =0 и x = l
n = 1, 2, …
1. Собственные значения энергии
2. Собственные волновые функции
3. Амплитуду а найдем
по условию нормировки
Слайд 186Линейный гармонический осциллятор
Решая данное уравнение, получаем:
n = 1, 2, …
1. Собственные значения энергии
2. Формулу Планка
При больших квантовых числах
3. Нулевая
энергия гармонического осциллятораСлайд 188Разность фаз.
Оптическая разность хода
Разность фаз
Уравнение гармонического колебания
Оптическая разность хода
Слайд 189Взаимодействие ЭМ волны с металлом
103—105 см–1
движение свободных электронов
под действием ЭП световой волны
выделение джоулевой теплоты
ЭП световой волны
свободные электроны
быстропеременные
токиэнергия световой волны быстро уменьшается, превращаясь во внутреннюю энергию металла
металлы непрозрачны для света
Чем выше проводимость металла
тем сильнее в нем поглощение света
возникно-вение
действует на
Слайд 190Александр Григорьевич Столетов
Российский физик.
Получил кривую намагничивания железа (1872), систематически исследовал
внешний фотоэффект (1888—1890), открыл первый закон фотоэффекта. Исследовалгазовый разряд, критическое состояние и
другие явления. Основал физическую лабораторию в Московском университете (1874).Основные работы в области электромагнетизма, оптики, молекулярной физики, философии.
Первым показал, что при увеличении намагничивающего поля магнитная восприимчивость железа сначала растёт, а затем, после достижения максимума, уменьшается (1872).
Снял кривую магнитной проницаемости ферромагнетика (кривая Столетова).
Автор двух методов магнитных измерений веществ (метод тороида с замкнутой магнитной цепью и баллистическое измерение намагниченности).
Провёл ряд экспериментов по измерению величины отношения электромагнитных и электростатических единиц, получил значение, близкое к скорости света (1876).
Провёл цикл работ по изучению внешнего фотоэффекта, открытого в 1887 году Г. Герцем (1888—1890).
Создал первый фотоэлемент, основанный на внешнем фотоэффекте. Рассмотрел инерционность фототока и оценил его запаздывание в 0,001 с.
Открыл прямо пропорциональную зависимость силы фототока от интенсивности падающего на фотокатод света (первый закон внешнего фотоэффекта, закон Столетова).
Открыл явление понижения чувствительности фотоэлемента со временем (явление фотоэлектрического утомления) (1889).
Основоположник количественных методов исследования фотоэффекта.
Автор метода фотоэлектрического контроля интенсивности света.
Исследовал несамостоятельный газовый разряд.
Обнаружил постоянство отношения напряжённости электрического тока к давлению газа при максимальном токе (константа Столетова).
Провёл цикл работ по исследованию критического состояния вещества (1892—1894).
10 августа 1839 – 27 мая 1896 Россия, Москва
Слайд 191Альберт Эйнштейн
Физик-теоретик, один из основателей современной теоретической физики
лауреат Нобелевской премии по физике 1921
года, общественный деятель-гуманист. Жил в Германии (1879—1893, 1914—1933), Швейцарии (1893—1914) и США (1933—1955).
Почётный доктор около 20
ведущих университетов мира, член многих Академий наук, в том числе иностранный почётный член АН СССР (1926).Эйнштейн — автор более 300 научных работ по физике, а также около 150 книг и статей в области истории и философии науки, публицистики и др.
Он разработал несколько значительных физических теорий:
Специальная теория относительности (1905).
В её рамках — закон взаимосвязи массы и энергии: E = mc2.
Общая теория относительности (1907—1916).
Квантовая теория фотоэффекта и теплоёмкости.
Квантовая статистика Бозе — Эйнштейна.
Статистическая теория броуновского движения, заложившая основы теории флуктуаций.
Теория индуцированного излучения.
Теория рассеяния света на термодинамических флуктуациях в среде[2]
Он также предсказал «квантовую телепортацию» и гиромагнитный эффект Эйнштейна — де Хааза. С 1933 года работал над проблемами космологии и единой теории поля. Активно выступал против войны, против применения ядерного оружия, за гуманизм, уважение прав человека, взаимопонимание между народами.
Эйнштейну принадлежит решающая роль в популяризации и введении в научный оборот новых физических концепций и теорий. В первую очередь это относится к пересмотру понимания физической сущности пространства и времени и к построению новой теории гравитации взамен ньютоновской. Эйнштейн также, вместе сПланком, заложил основы квантовой теории. Эти концепции, многократно подтверждённые экспериментами, образуют фундамент современной физики
14 марта 1879 Германия –
18 апреля 1955 США
Albert Einstein
Слайд 192Макс Планк
Макс Карл Эрнст Людвиг Планк[1] (нем. Max Karl Ernst Ludwig Planck; 23
апреля 1858, Киль — 4 октября 1947, Гёттинген) — выдающийся немецкий физик. Как основатель квантовой теории предопределил основное направление
развития физики с начала XX века.Слайд 193Иоганн Кеплер
Немецкий математик, астроном, оптик и астролог.
Открыл законы движения планет.
Johannes
Kepler
27 декабря 1571 – 15 ноября 1630 Германия
Слайд 194Густав Людвиг Герц
Немецкий физик, лауреат Нобелевской премии по физике 1925г.
«за открытие законов соударения электрона с атомом» (совместно с Джеймсом
Франком)Племянник знаменитого Генриха Герца
1945-1954 – возглавлял исследовательскую лабораторию (Сухуми)
Лауреат Сталинской премии за исследования динамики и устойчивости каскадов газодиффузионного разделения изотопов урана
В 1955 г. – руководитель научного совета по мирному применению атомной энергии при совете министров ГДР
22 июля 1887— 30 октября 1975, Германия
Gustav Ludwig Hertz
Слайд 195Луиджи Гальвани
1737-1798
Италия
Александр Григорьевич Столетов
1839-1896
Россия, Москва
Филипп Эдуард Антон фон Ленард
1862-1947
Германия
Альберт Эйнштейн
Albert Einstein
1879-1955
Германия, США
Слайд 196Йозеф Стефан
Австрийский физик и математик
Член Австрийской академии наук (1865)
24 марта
1835 – 7 января 1893, Австрия
Joseph Stefan
Слайд 197нем. Ludwig Eduard Boltzmann, 20 февраля 1844, Вена, Австрийская империя
— 5 сентября 1906, Дуино, Италия — австрийский физик-теоретик, основатель
статистической механики и молекулярно-кинетической теории. Член Австрийской академии наук (1895), член-корреспондент Петербургской академии наук (1899) и ряда других.ученик Й.Стефана
Слайд 198Вильгельм Карл Вернер Отто Фриц Франц ВИН
Немецкий физик
Окончил Берлинский университет
в 1886
1892-1896 приват-доцент Берлинского университета
1896-1899 профессор Высшей технической школы в
Ахенес 1900 профессор Вюрцбургского, затем Мюнхенского университетов
В 1893 вывел теоретический закон излучения абсолютно чёрного тела и показал, что максимум энергии излучения должен смещаться по спектру излучения с ростом температуры
1911 – Нобелевская премия за изучение теплового излучения
Исследовал отклонение каналовых лучей в электрическом и магнитном полях, разработал метод измерения длительности свечения свободных атомов
Один из авторов многотомного «Руководства по экспериментальной физике»
Wilhelm Wien
13 января 1864 – 30 августа1928, Германия
Слайд 199Эрвин Шрёдингер
Австрийский физик-теоретик
Автор ряда фундаментальных результатов
в области квантовой теории,
которые легли
в основу волновой механики:
сформулировал волновые уравнения (стационарное
и зависящее
от времени уравнения Шрёдингера),показал тождественность развитого им формализма и матричной механики,
разработал волновомеханическую теорию возмущений,
получил решения ряда конкретных задач,
предложил оригинальную трактовку физического смысла волновой функции
еоднократно подвергал критике общепринятую копенгагенскую интерпретацию квантовой механики (парадокс «кота Шрёдингера»)
Автор множества работ в различных областях физики:
статистической механике и термодинамике,
физике диэлектриков,
теории цвета,
электродинамике,
общей теории относительности и космологии;
предпринял несколько попыток построения единой теории поля
Erwin Schrödinger
12 августа 1887 – 4 января1961, Австрия
Слайд 200Джон Уильям Рэлей
Рэлей (Стретт) Джон Уильям (1842–1919) – английский физик.
Работы посвящены теории колебаний, одним из основоположников которой он является,
акустике, теории теплового излучения, молекулярной физике, гидродинамике, электромагнетизму, оптике. Исследовал колебания упругих тел, первый обратил внимание на автоколебания. Заложил основы теории молекулярного рассеяния света, объяснил голубой цвет неба. Сконструировал рефрактометр (рефрактометр Рэлея).Слайд 201Джинс Джеймс Хопвуд
Джинс Джеймс Хопвуд (1877–1946) – английский физик и
астрофизик. Основные физические исследования посвящены кинетической теории газов и теории
теплового излучения. Вывел в 1905 году формулу плотности энергии (закон Релея–Джинса). Работы Джинса посвящены также квантовой теории, математической теории электричества и магнетизма, теоретической механике, теории относительности.Слайд 202Джон Уильям Стретт
он же Барон Рэлей (Рэйли) III
Британский физик
Открыл (с
Уильямом Рамзаем) газ аргон, за это получил Нобелевскую премию по
физике в 1904 г.Открыл явление, называемое рассеянием Рэлея и предсказал существование поверхностных волн, которые также называются волнами Рэлея
1861-1871 гг. - Тринити-колледж Кембриджского университета: обучение, сотрудник факультета.
с 1873 г. член Лондонского королевского общества
1879-1884 гг. - второй Кавендишский профессор (после Джеймса Максвелла) этого университета и директор Кавендишской лаборатории
С 1887 - профессор Британского королевского института (Лондон)
1905-1908 гг. - председатель Лондонского королевского общества
1908-1919 гг. - глава Кембриджского университета
12 ноября 1842–
30 июня 1919, Англия
John William Strutt, Third Baron Rayleigh
Слайд 203Дмитрий Сергеевич Рождественский
Исследование аномальной дисперсии
создал Государственный оптический институт (ГОИ), 1918
создал авторитетную научную школу оптиков
один из организаторов оптической промышленности в
СССР1876-1940,
Россия,
Санкт-Петербург
Слайд 206Использованные источники
Трофимова Т.И. Курс физики
Костко О.К. Физика для строительных и
архитектурных вузов
Сахаров Д.И., Блудов М.И. Физика для техникумов
Ландсберг Г.С. Элементарный
учебник физикиhttp://aco.ifmo.ru/el_books/basics_optics/
http://all-fizika.com/
http://bse.sci-lib.com/
http://elementy.ru/physics
http://ens.tpu.ru/posobie.htm
http://fn.bmstu.ru/phys/bib/physbook/tom6/content.htm
http://physoptika.ru/
http://ru.wikipedia.org
http://rutube.ru/tracks/1425275.html?v=0ccd9cf27c52d982fb958fea16fb3057
http://school-collection.edu.ru
http://stoom.ru/content
http://tsput.ru/res/3.php
http://web.mit.edu/newsoffice/science.html
http://www.allbiograf.ru/category/fizika/
http://www.epsilon.cc/
http://www.fizika.kr.ua/index.php
http://www.ido.rudn.ru/nfpk/fizika/
http://www.kit-e.ru/articles/displ/2007_7_22.php
http://www.krugosvet.ru/enc/nauka_i_tehnika/
http://www.osram-auto.ru/prof/page1970/page8449/
http://www.physbook.ru/index.php/
http://www.seninvg07.narod.ru/s_portfolio_virt2.htm
http://www.varson.ru/
и др.



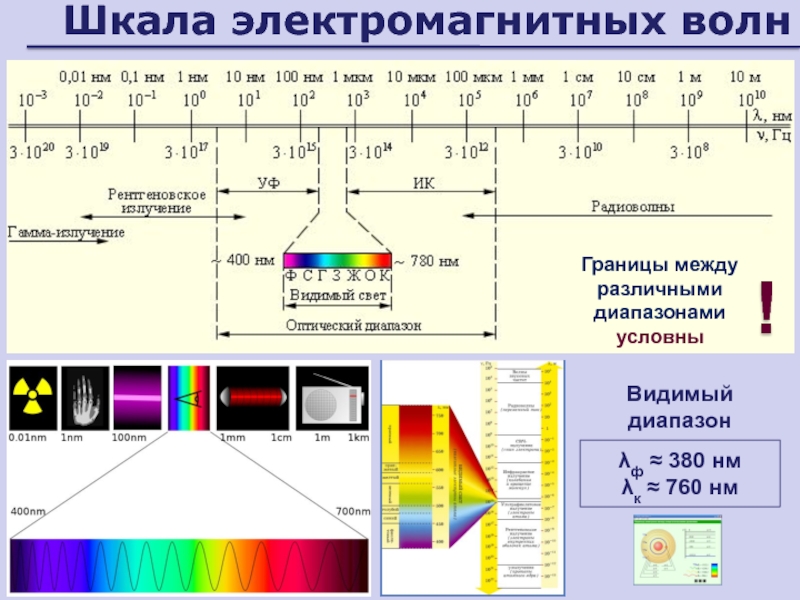
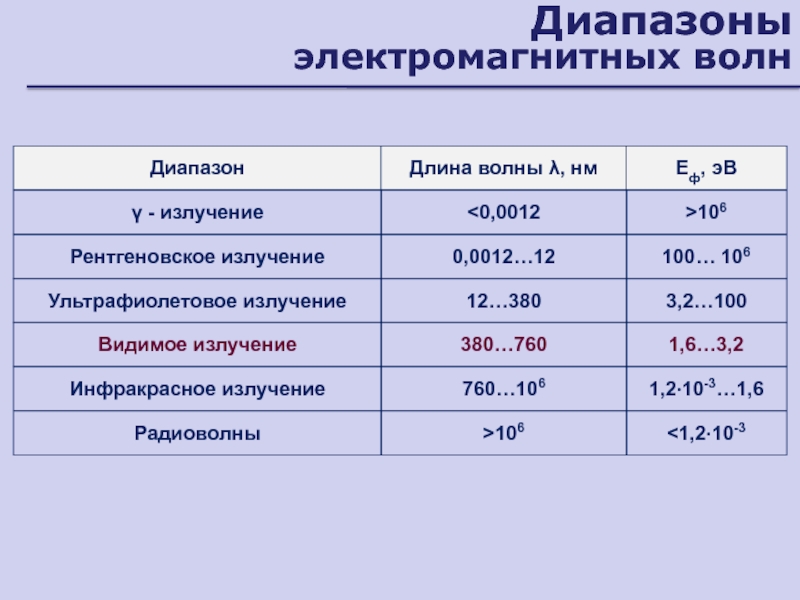
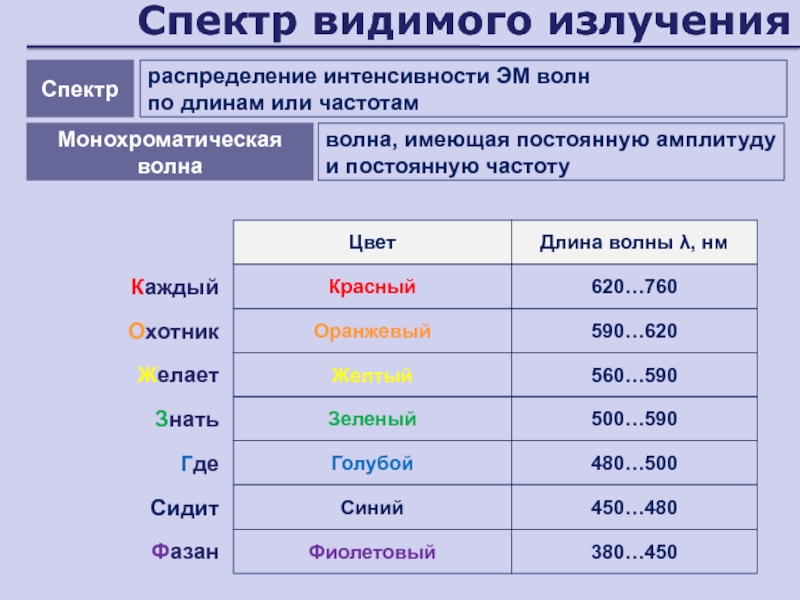
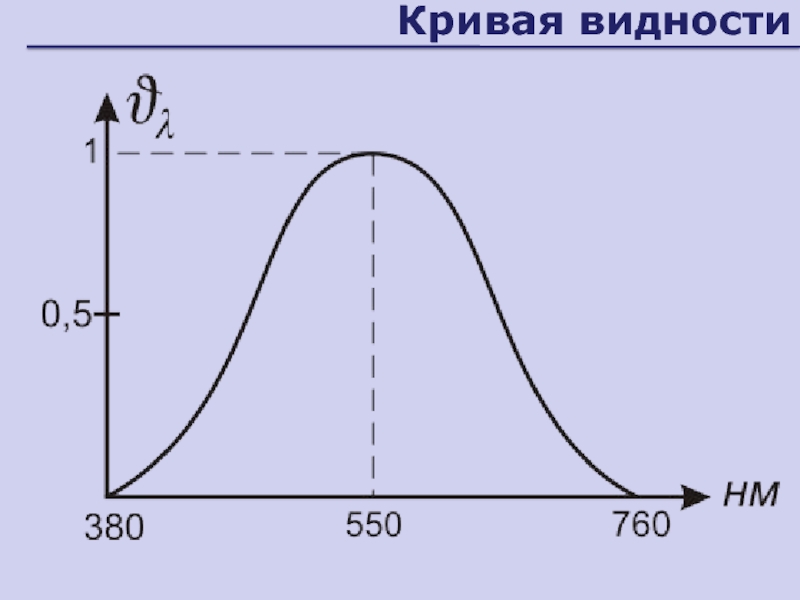


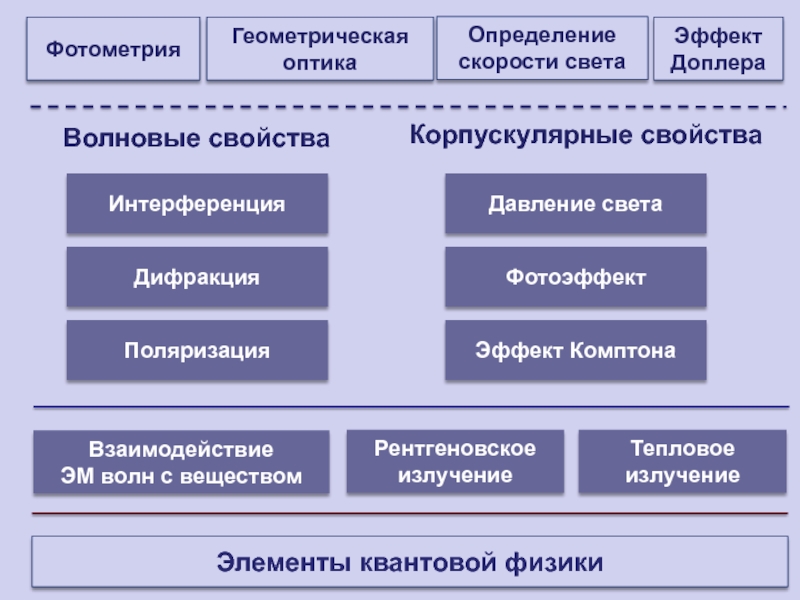

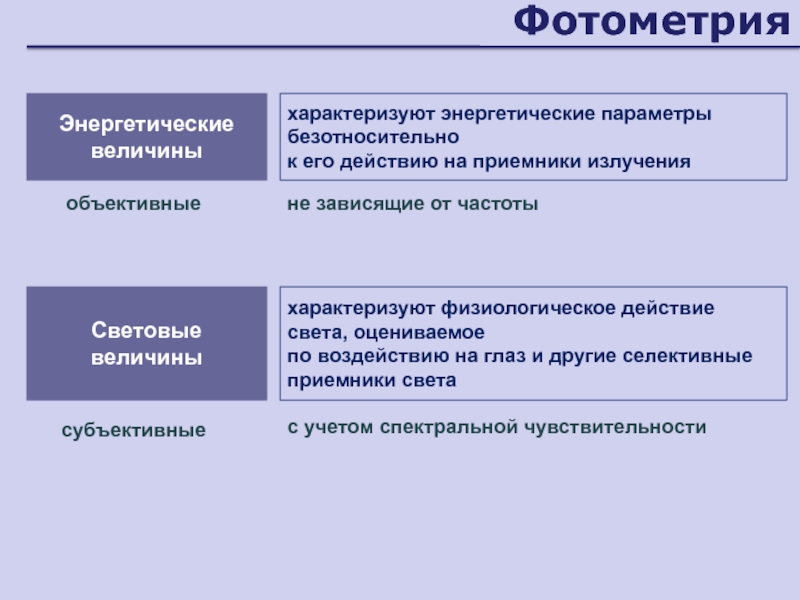
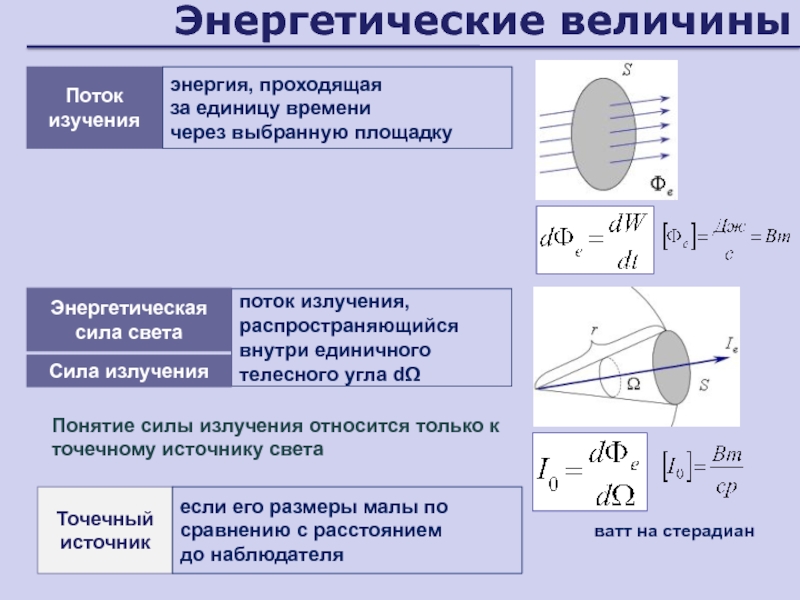
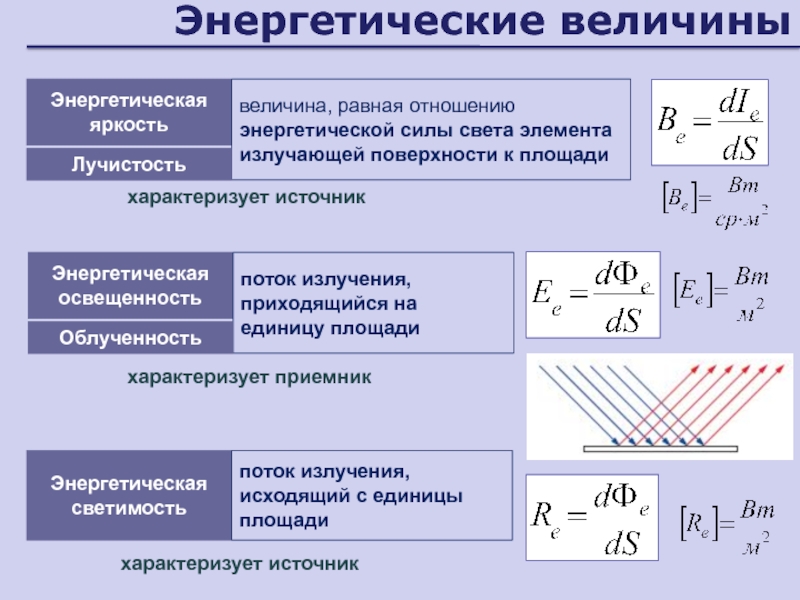

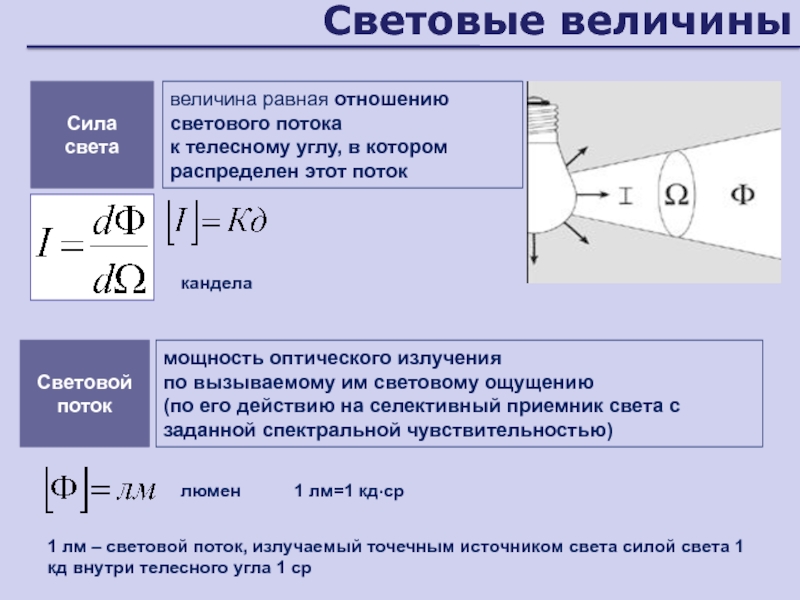
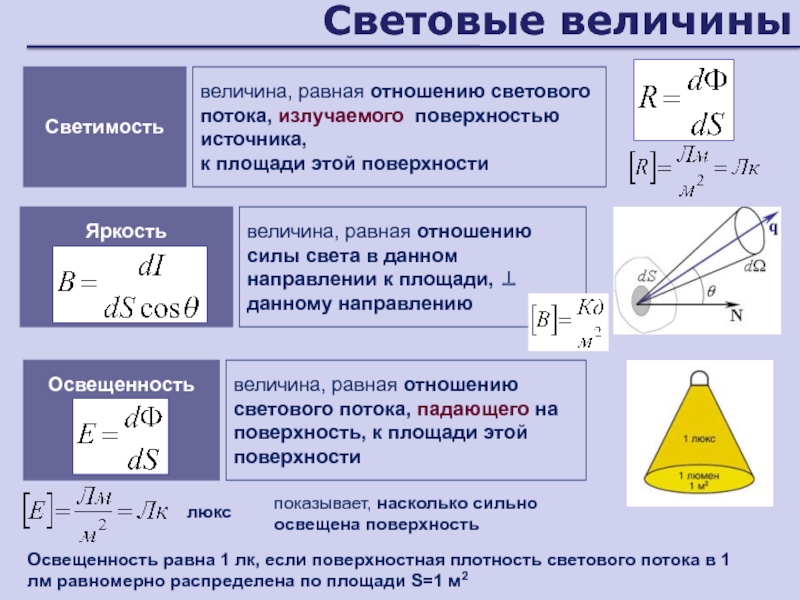

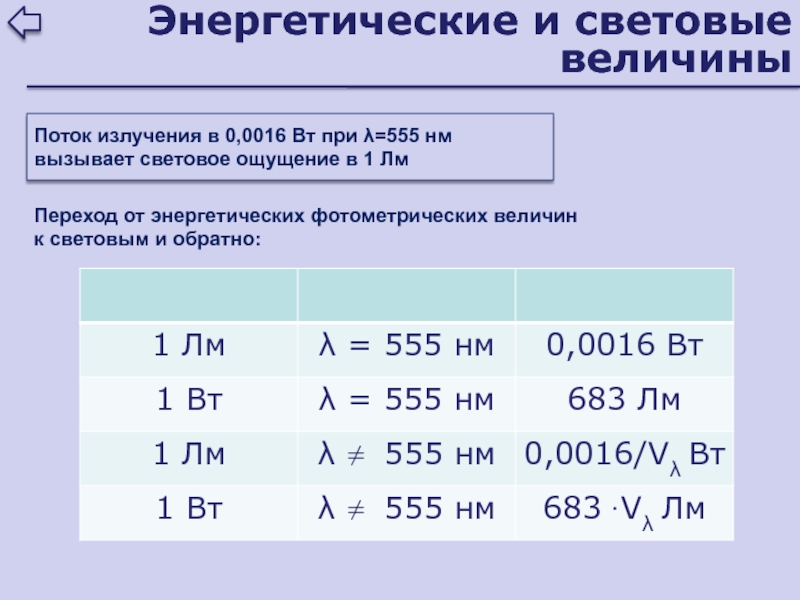


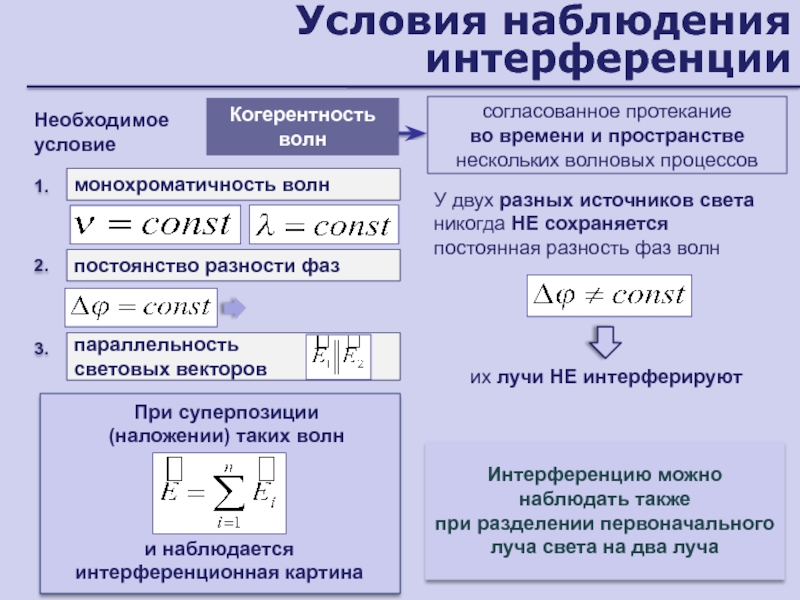
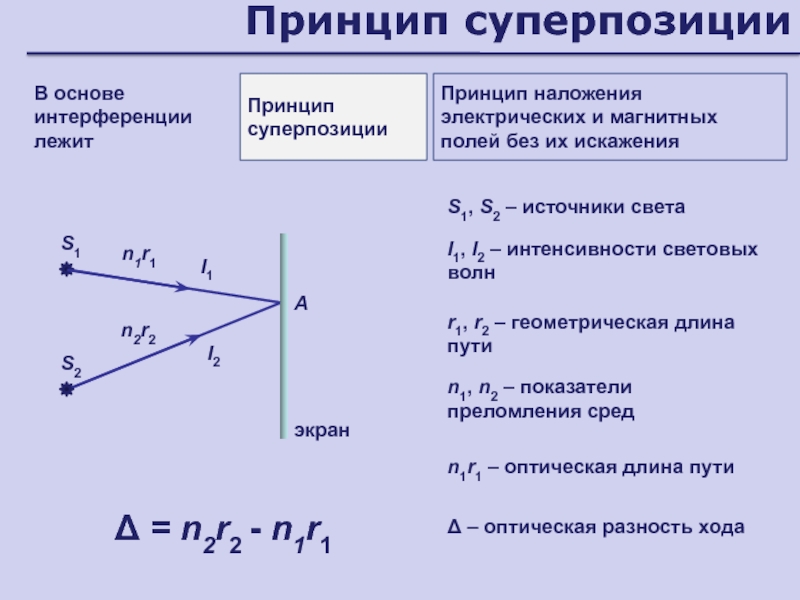
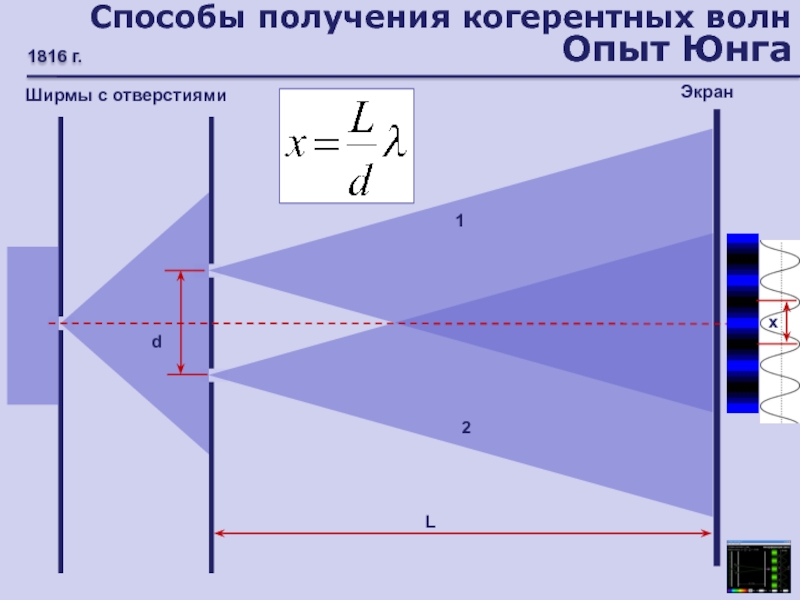
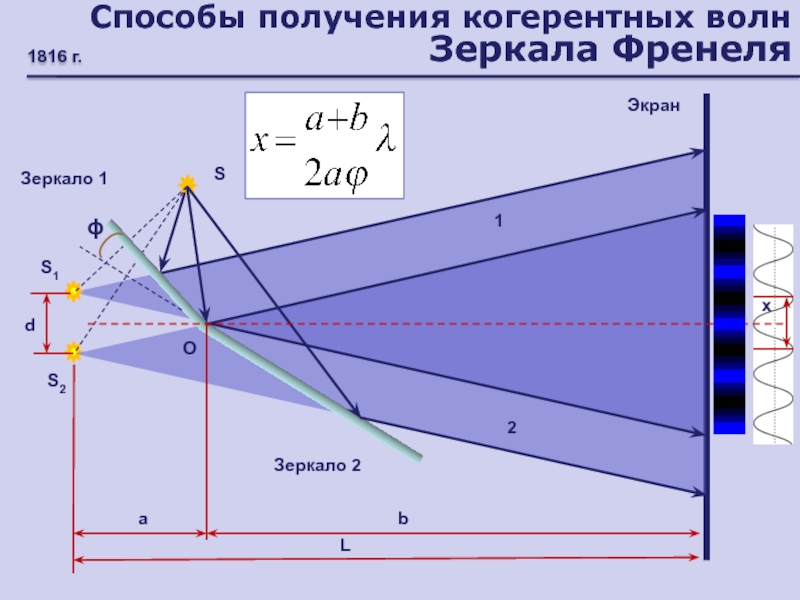
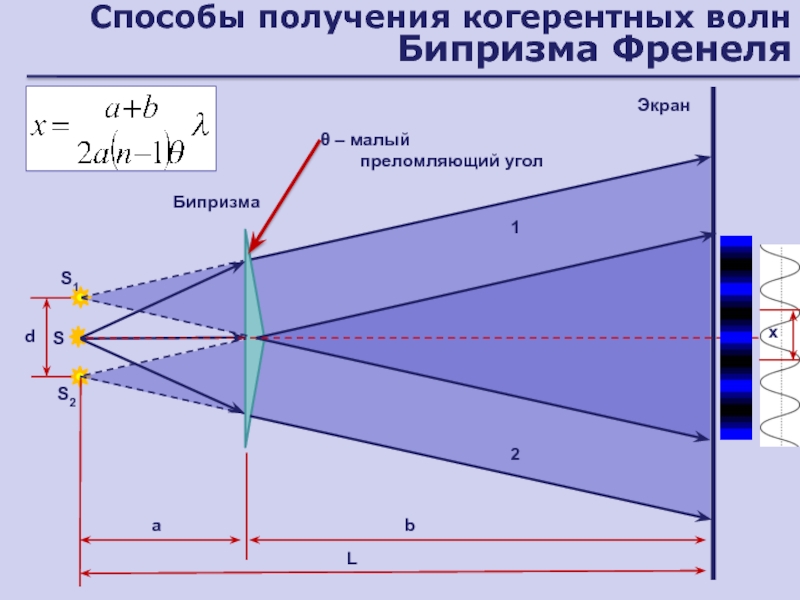

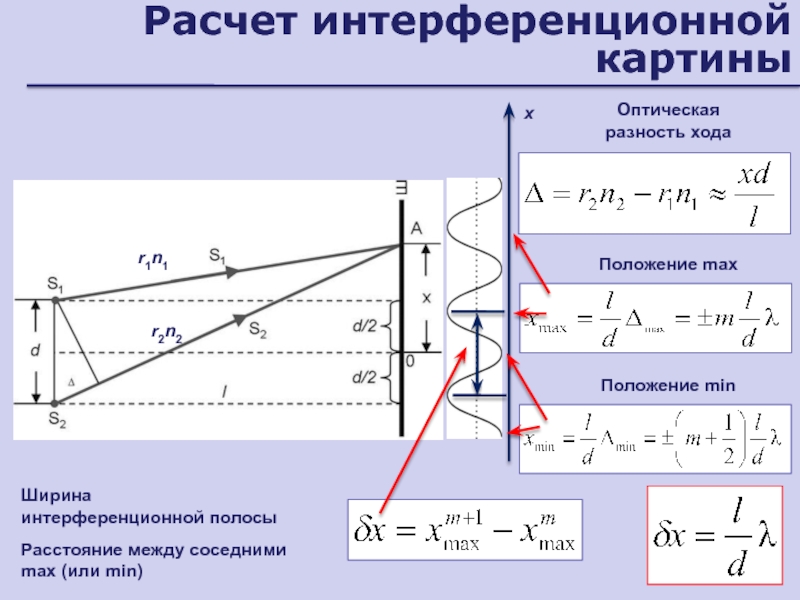
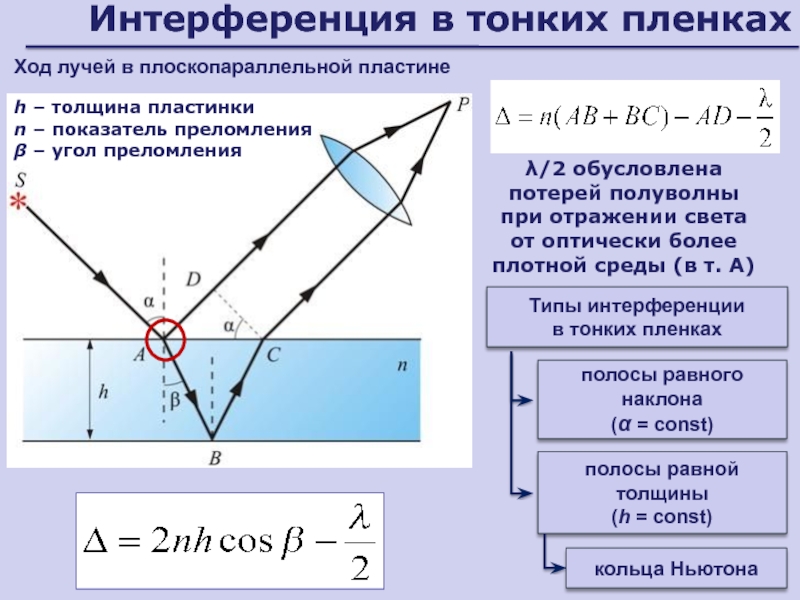
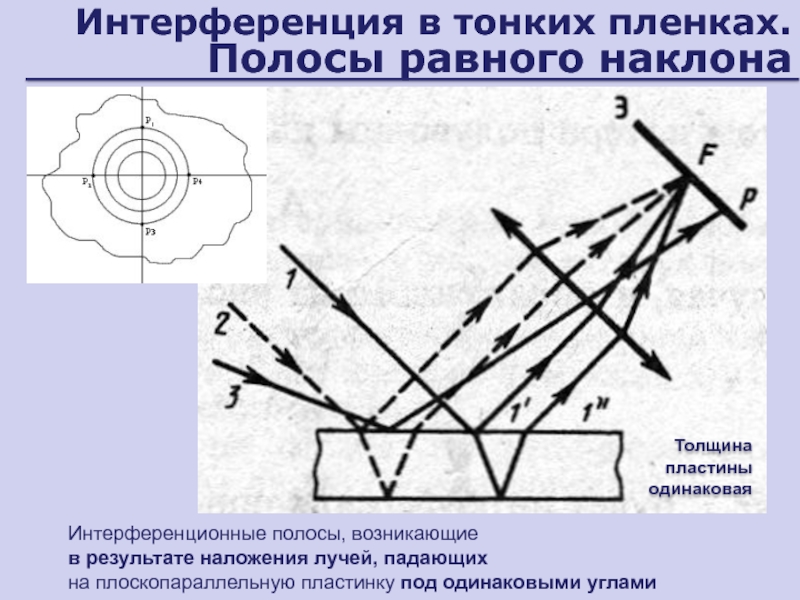
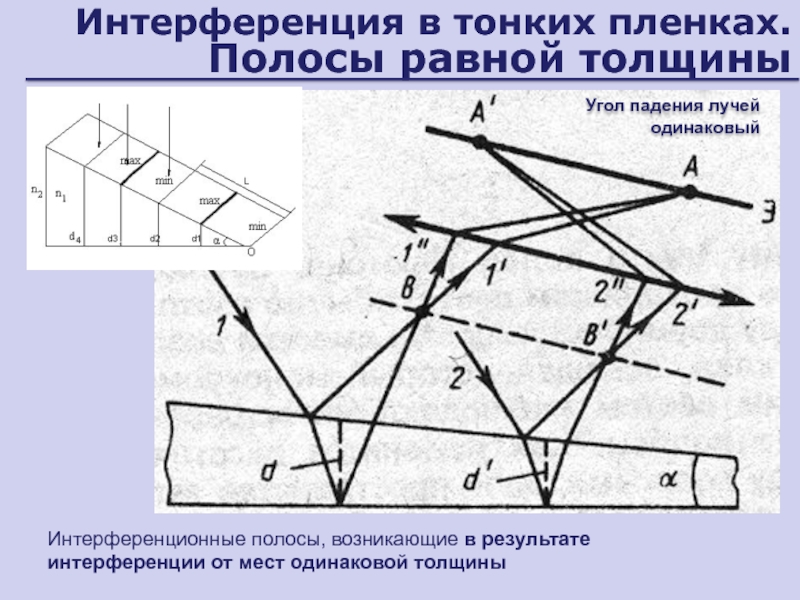
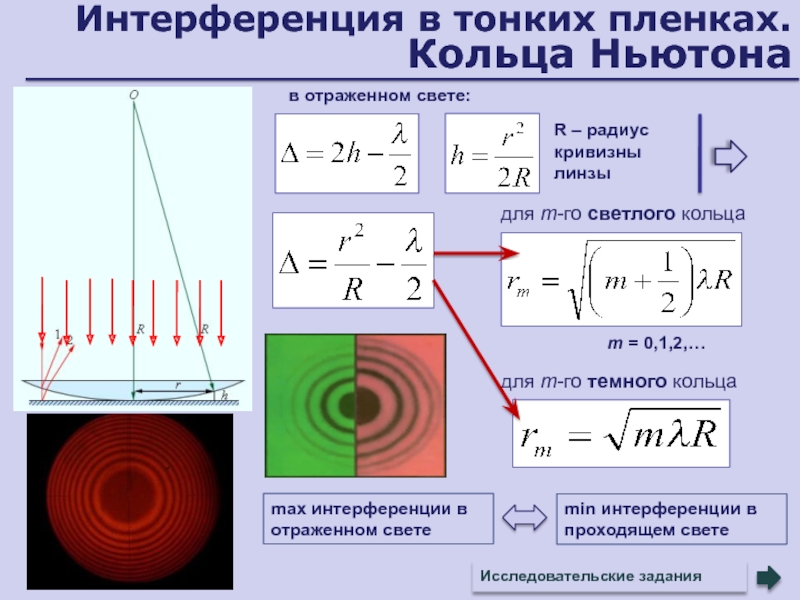
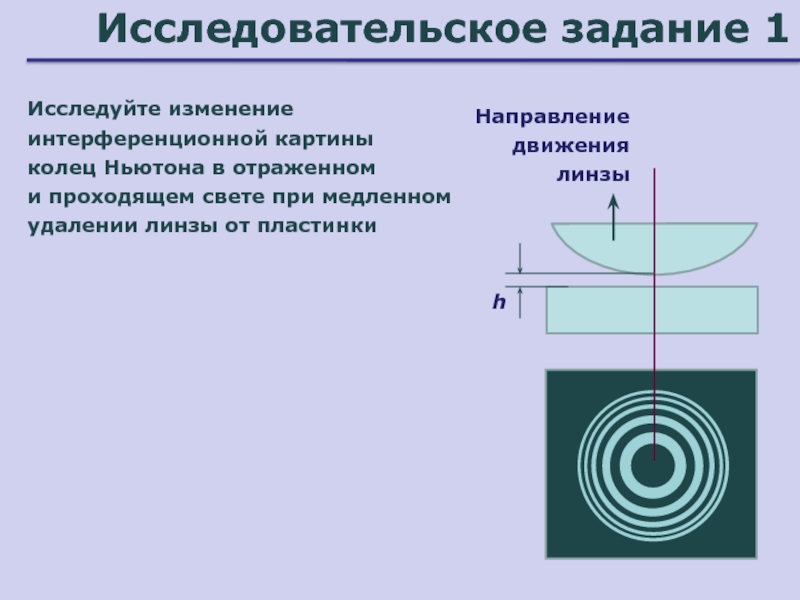
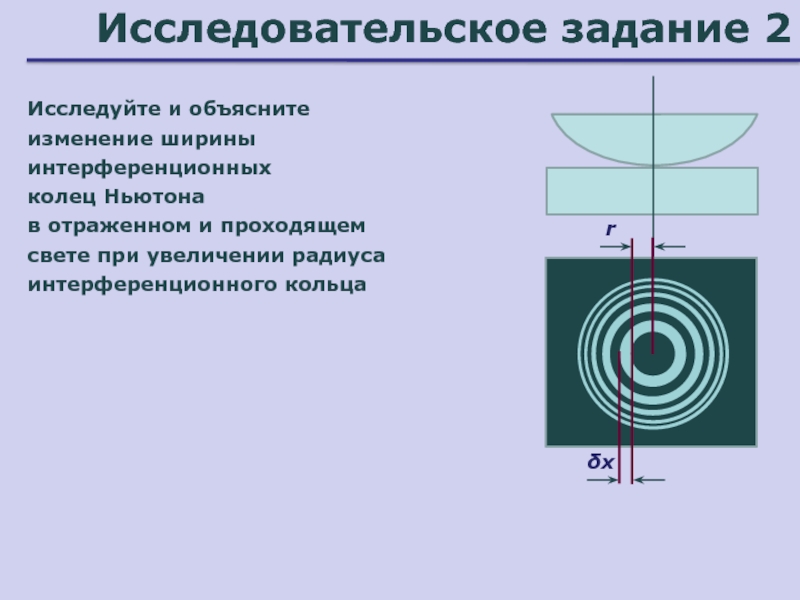
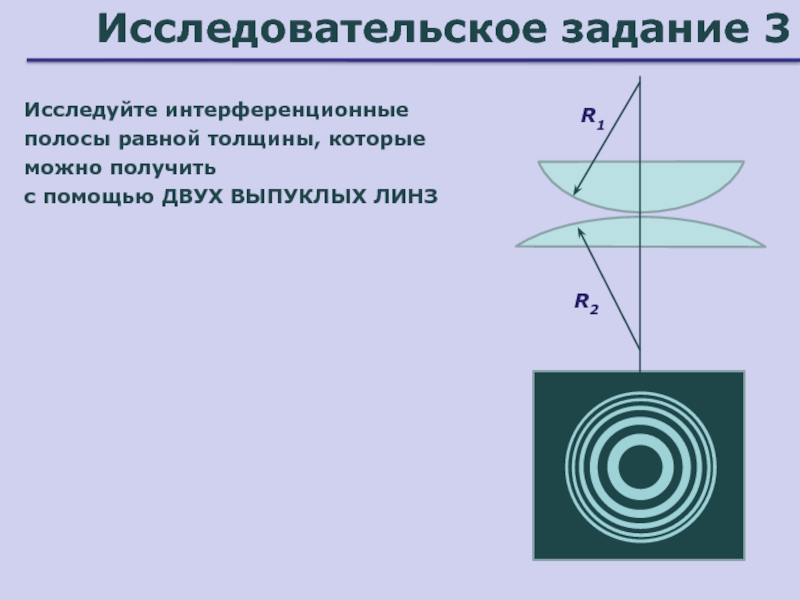
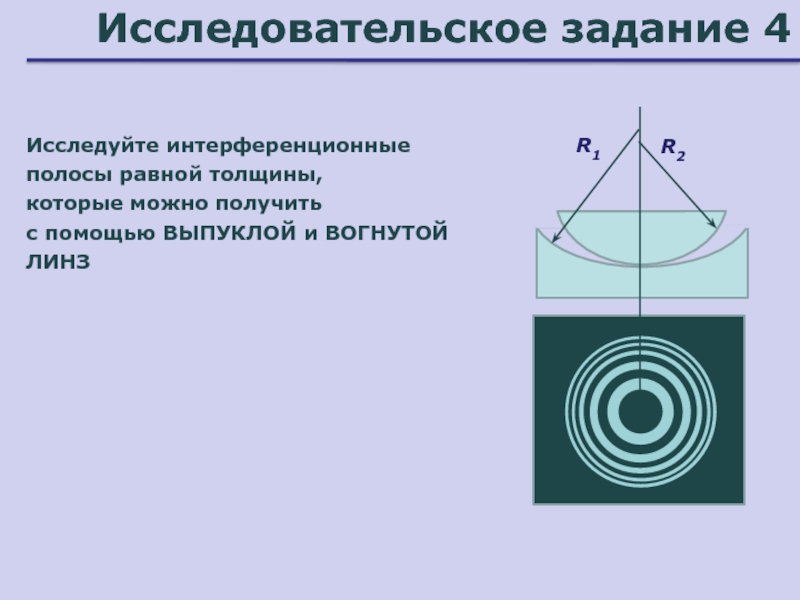
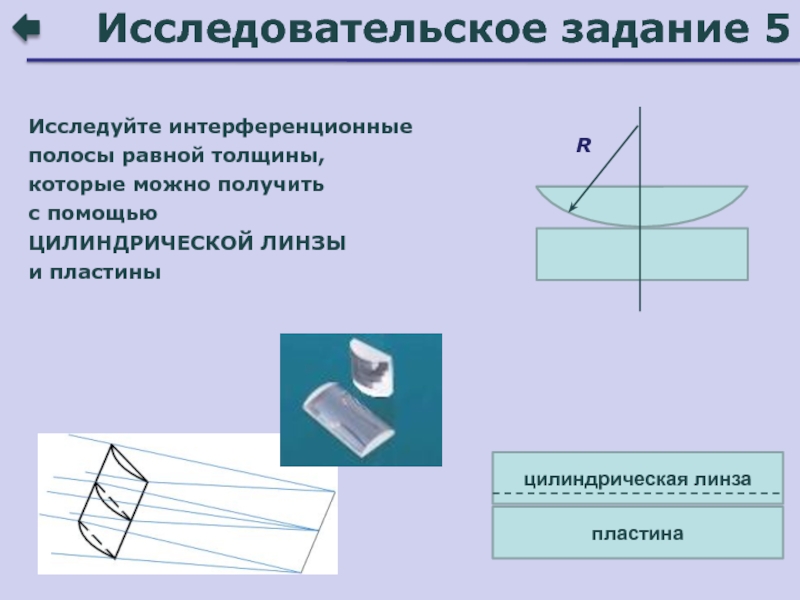
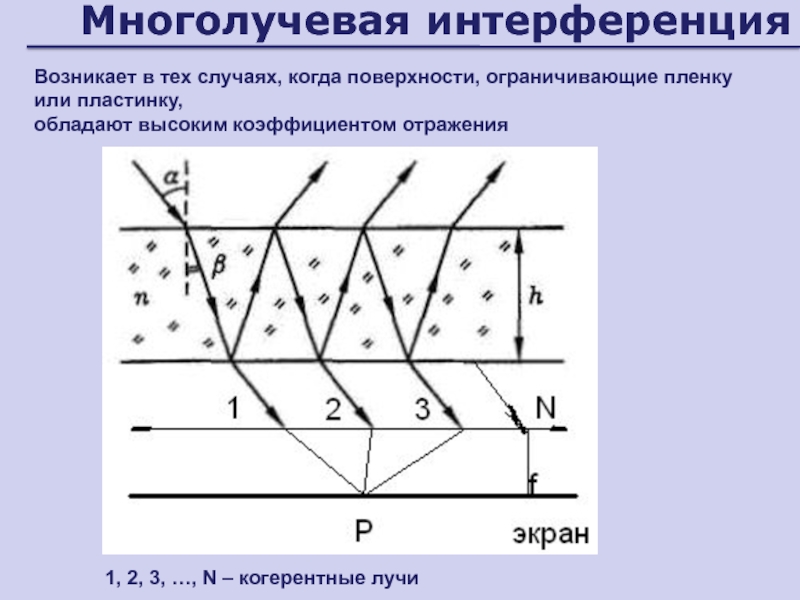
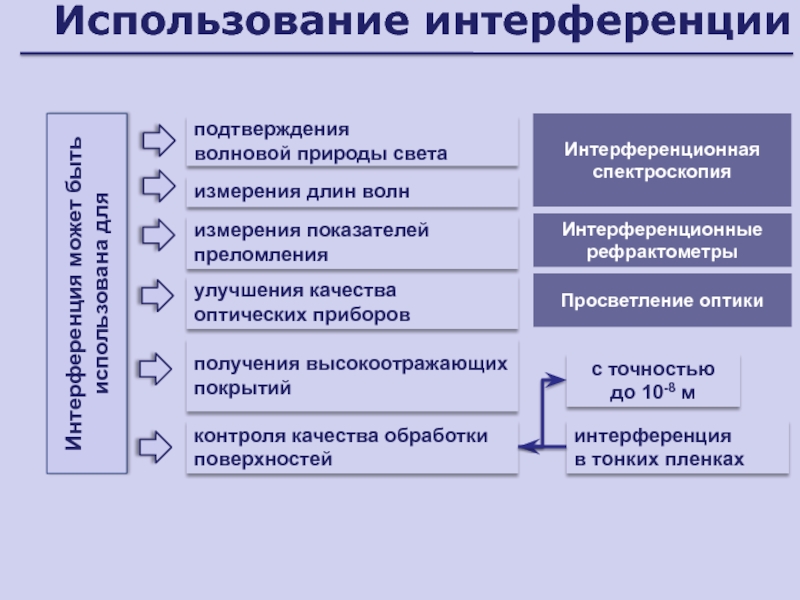

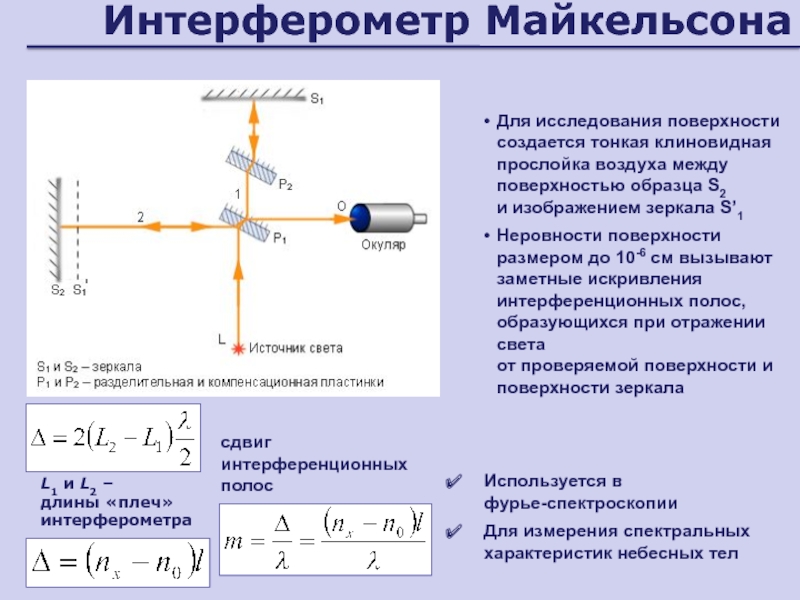
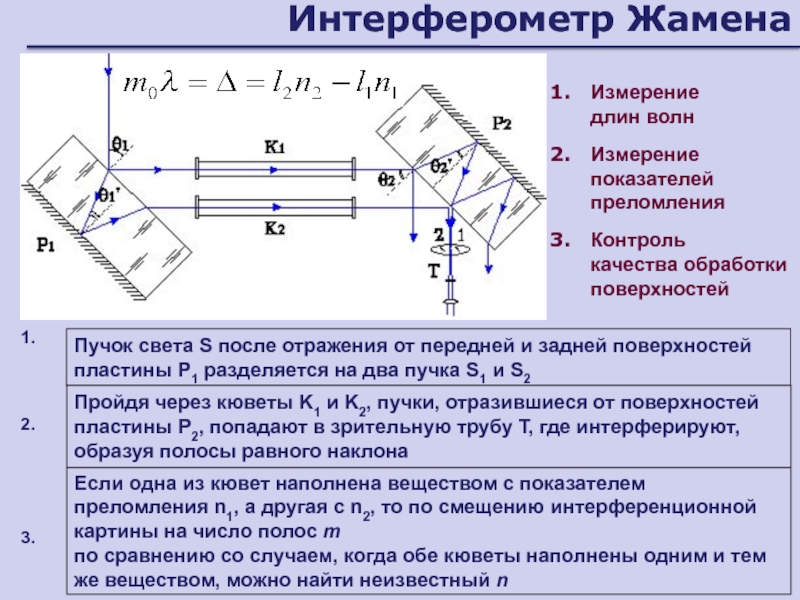
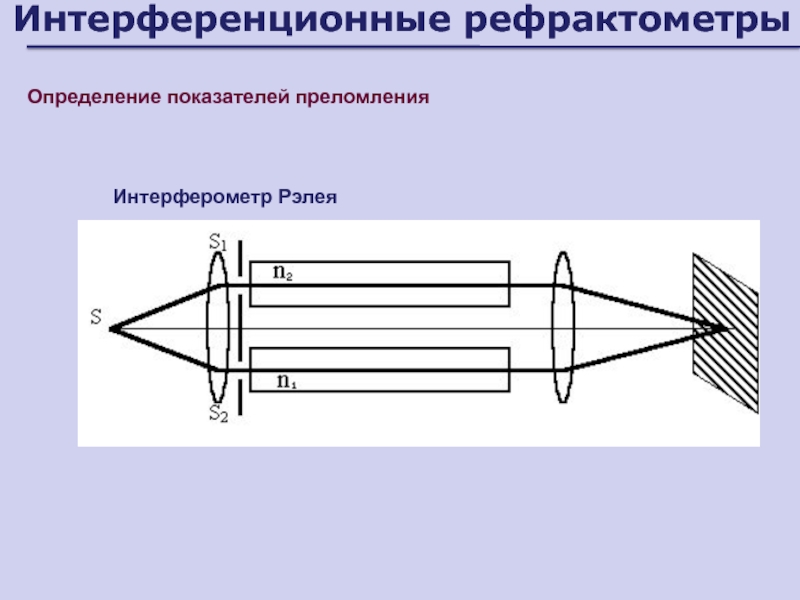
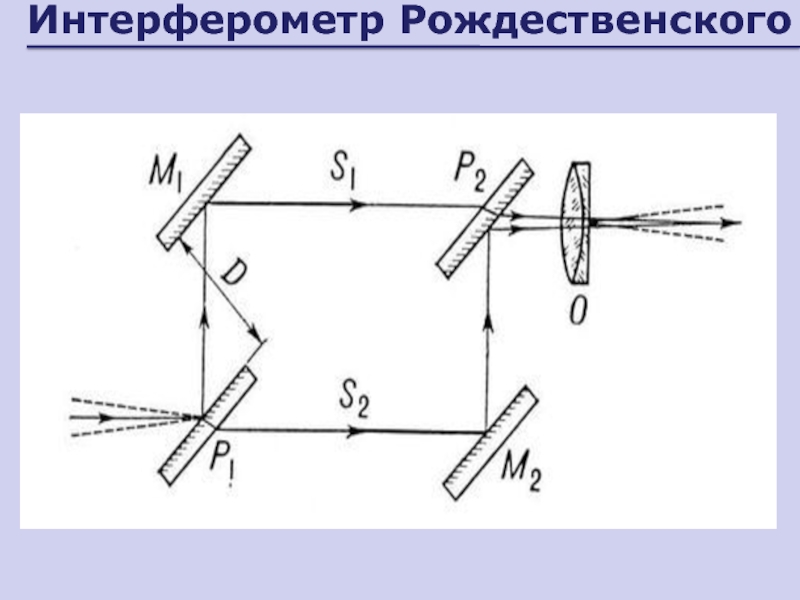
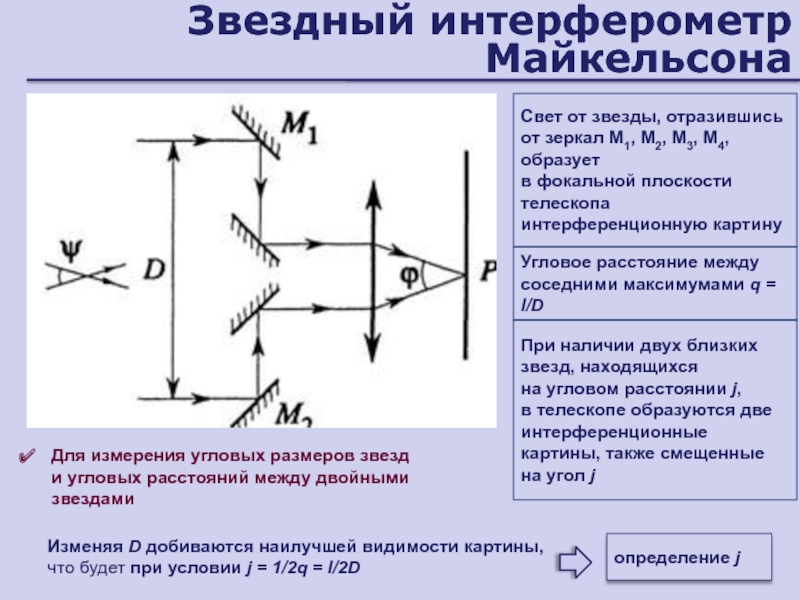
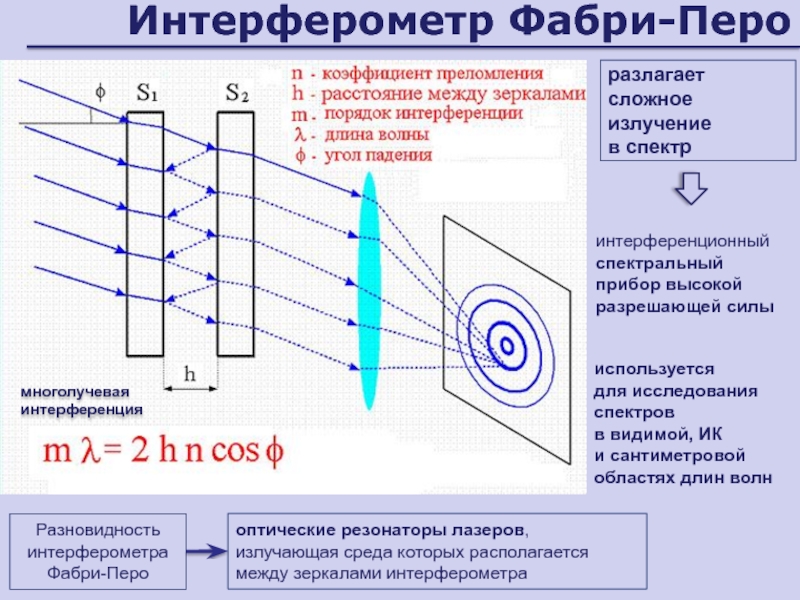
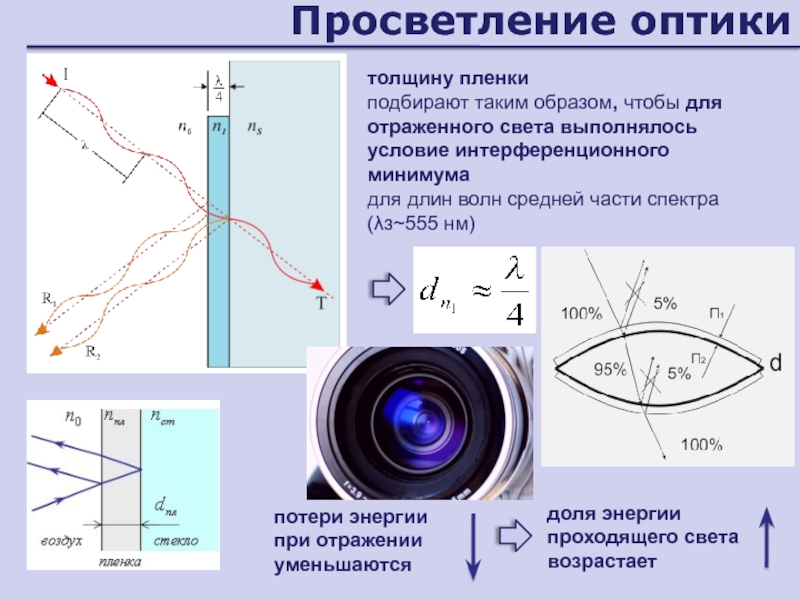
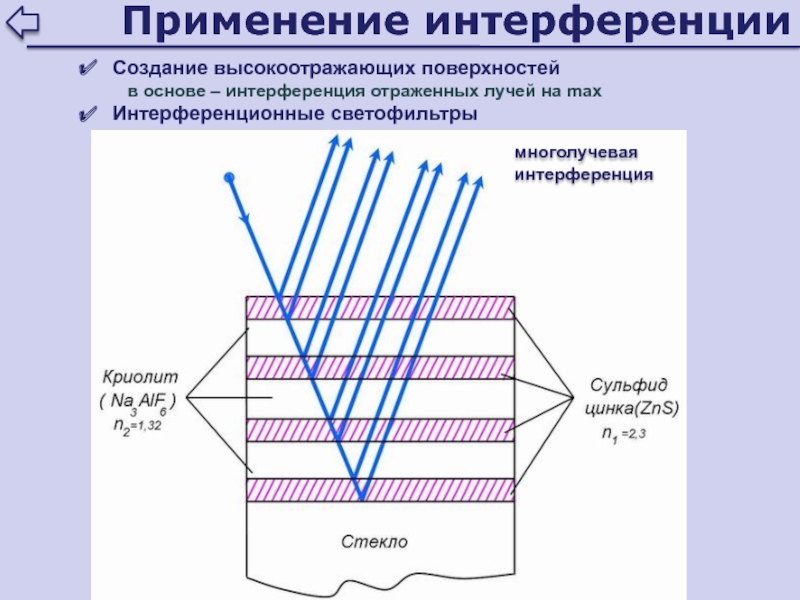

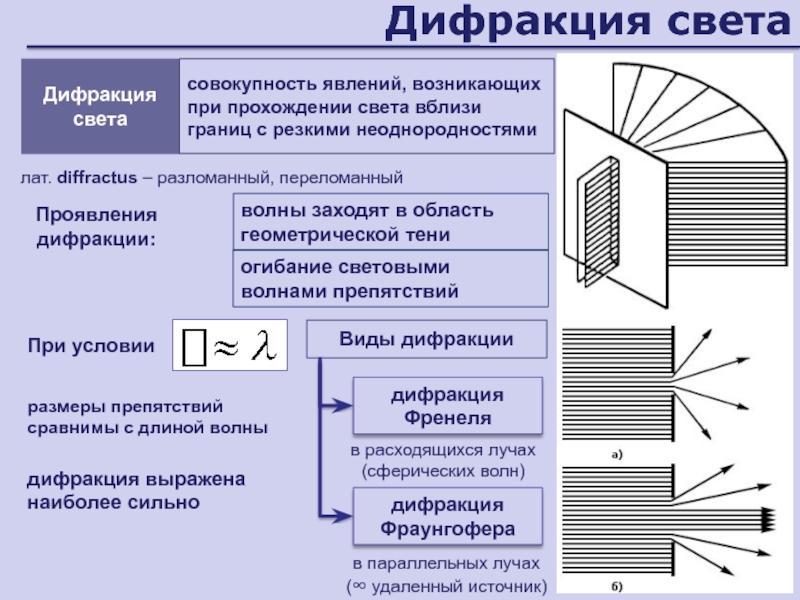
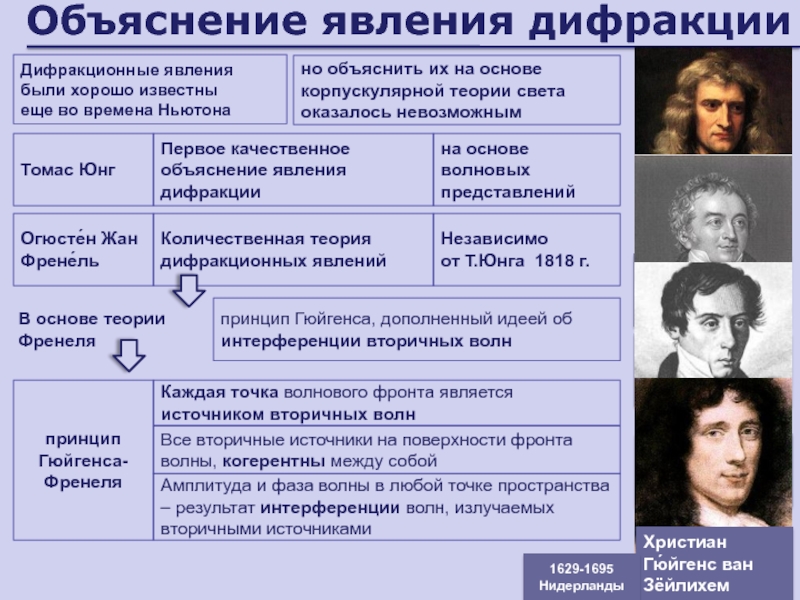
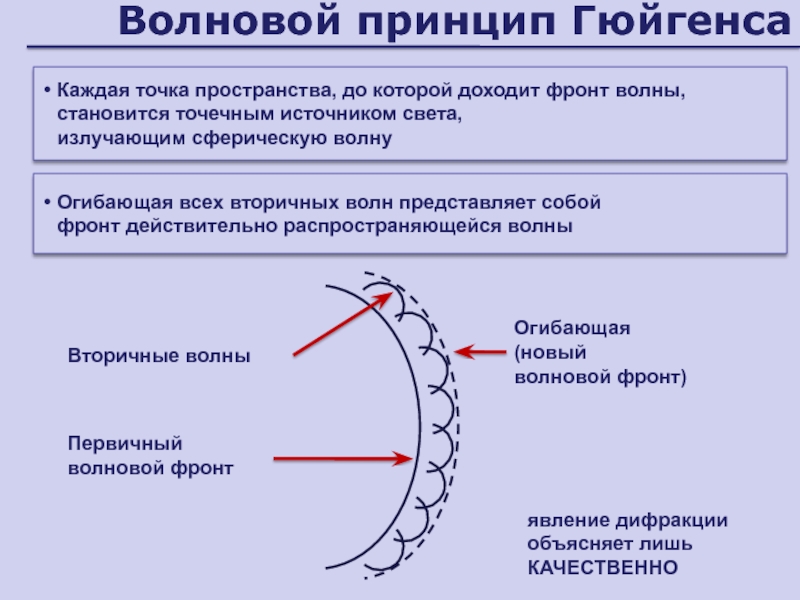
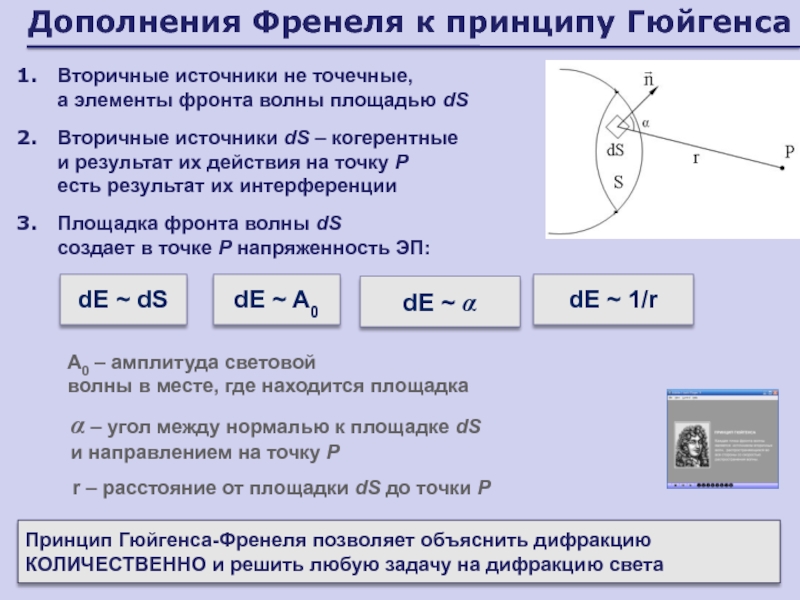
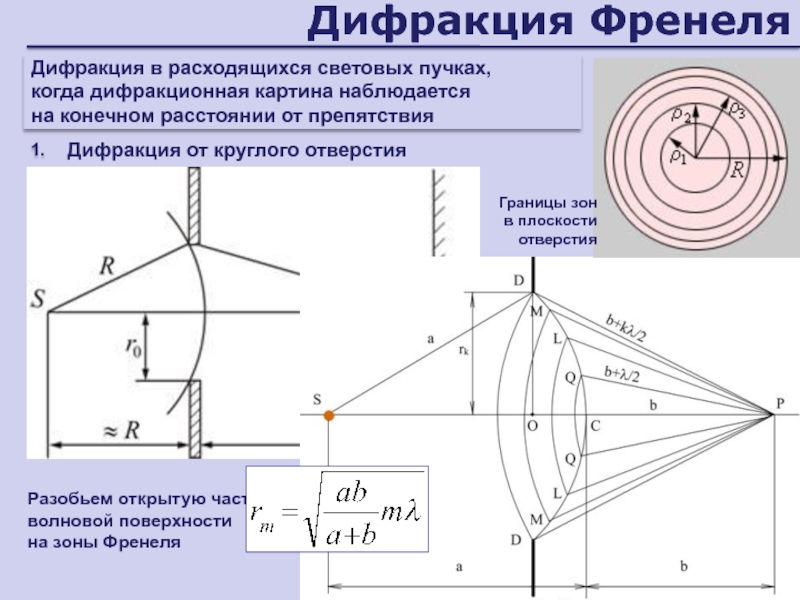
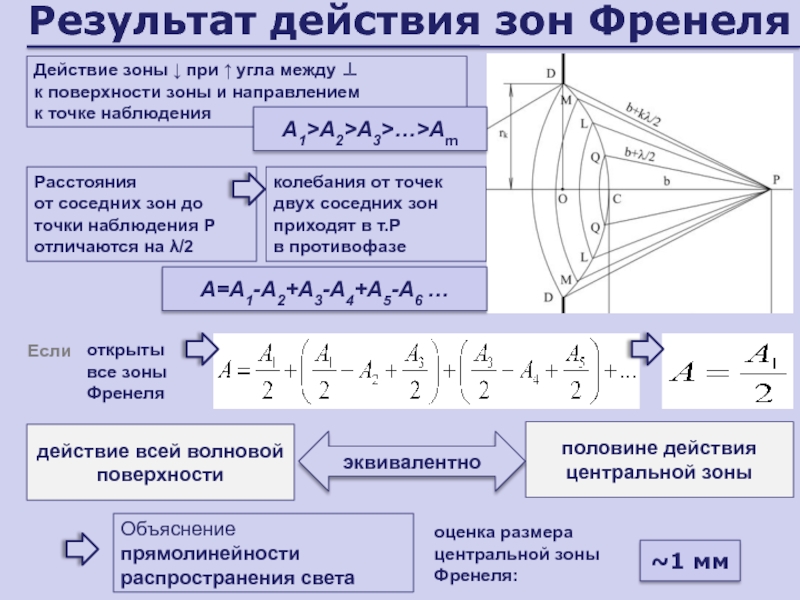
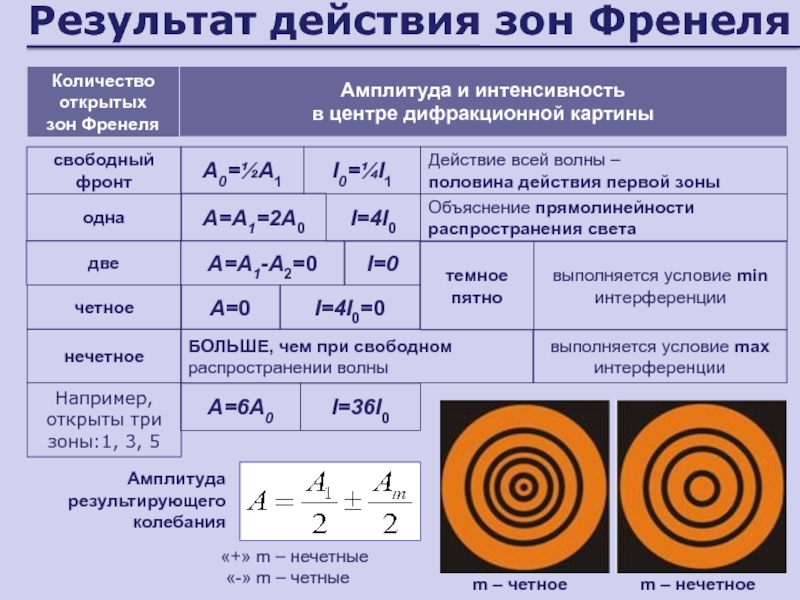
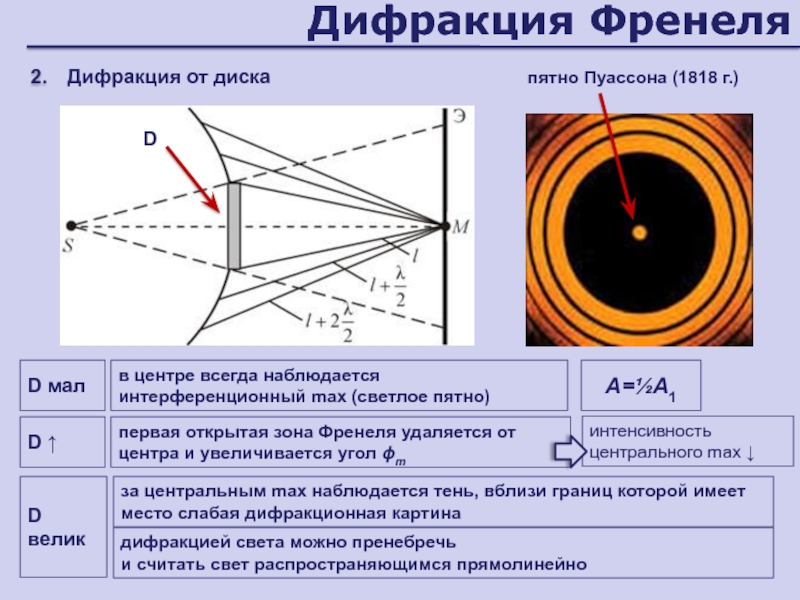
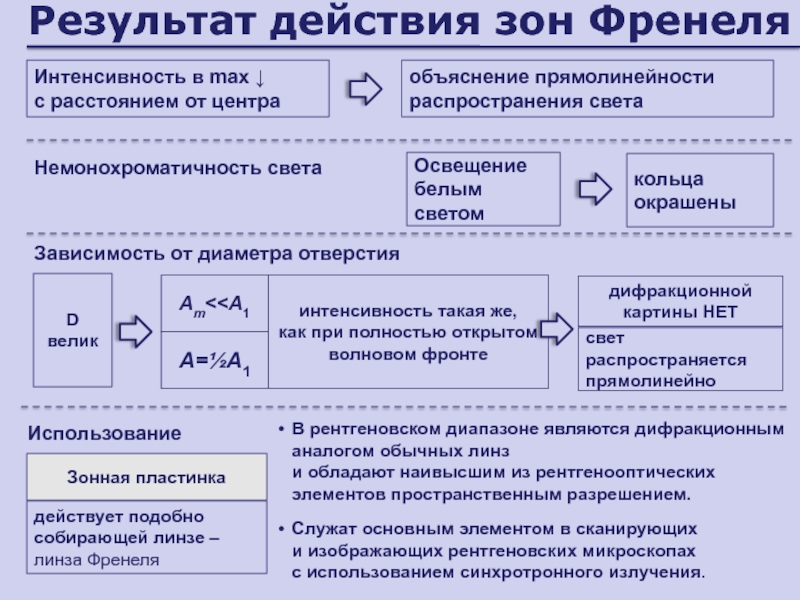
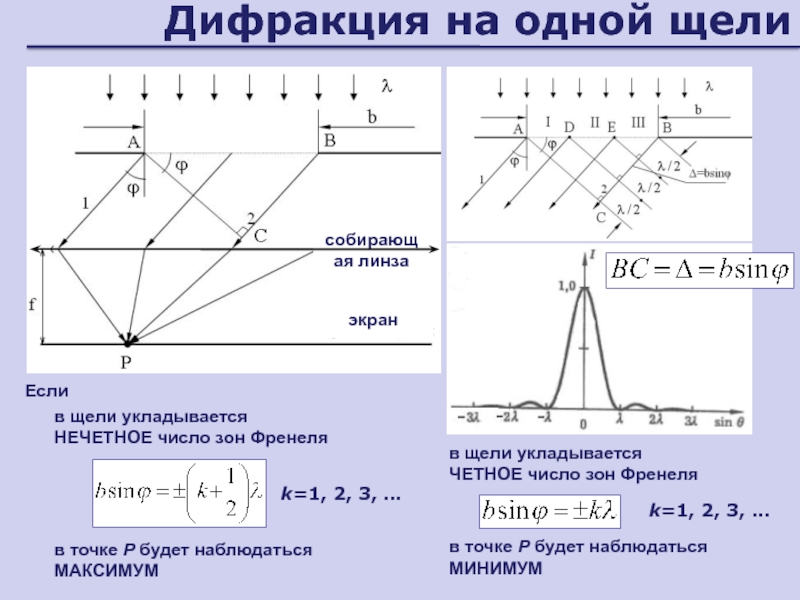
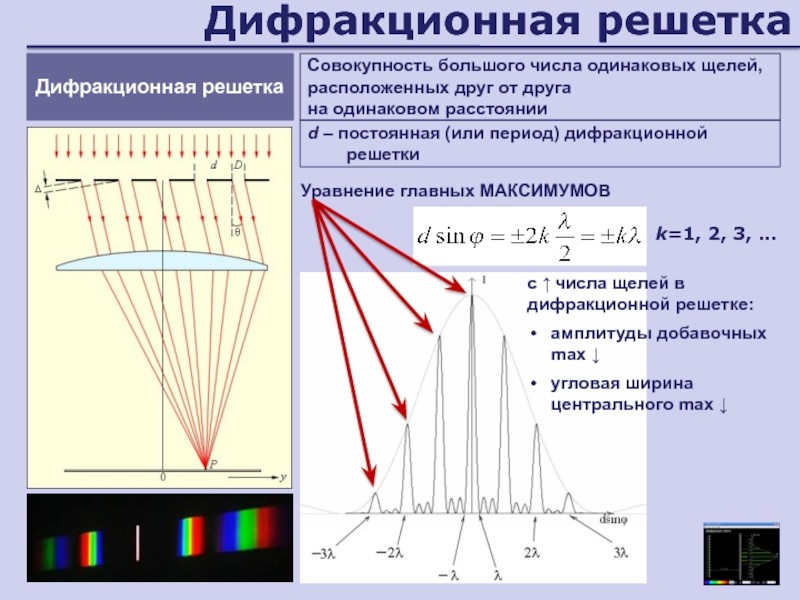
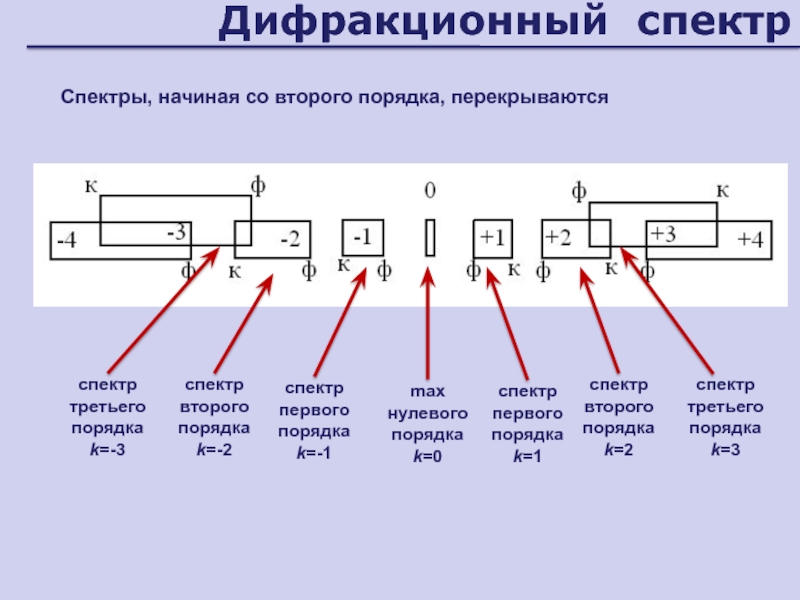
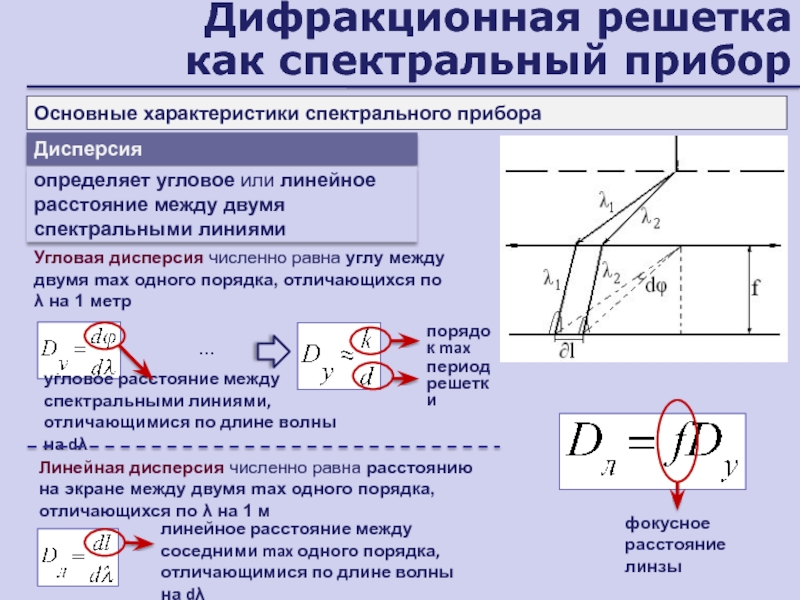
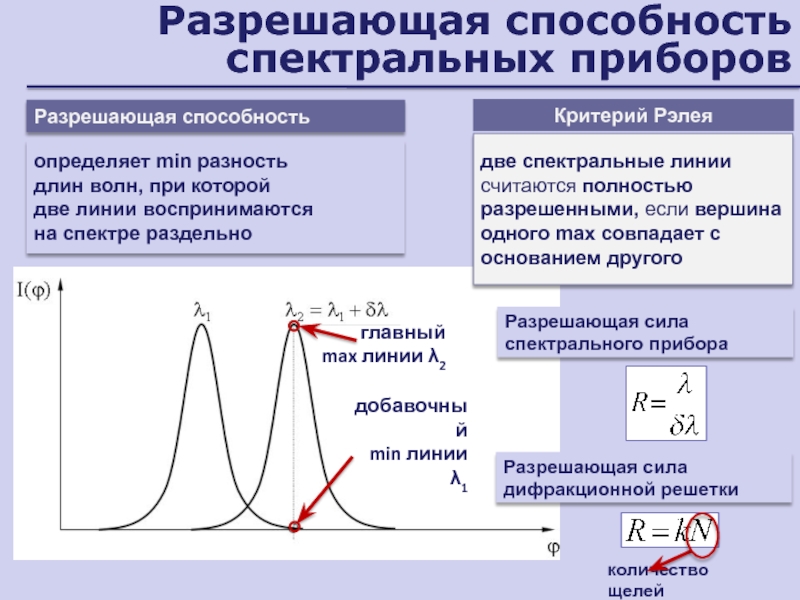
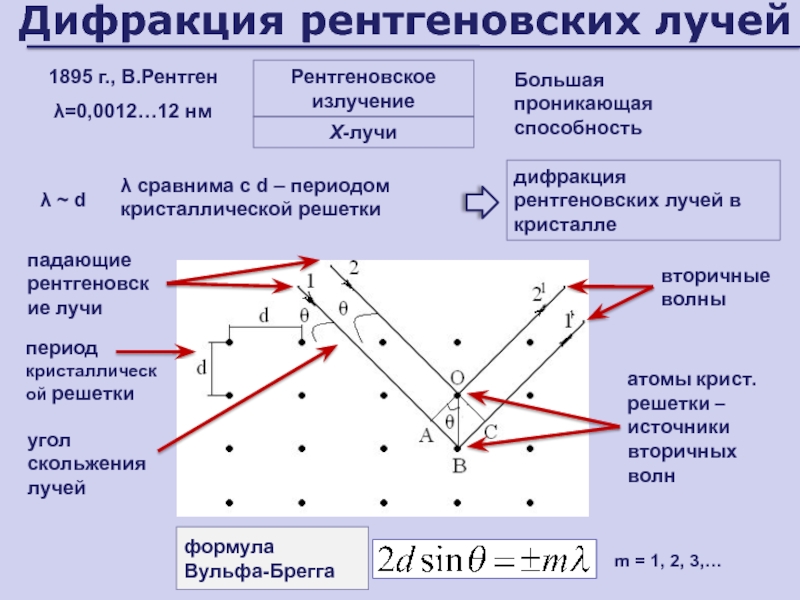
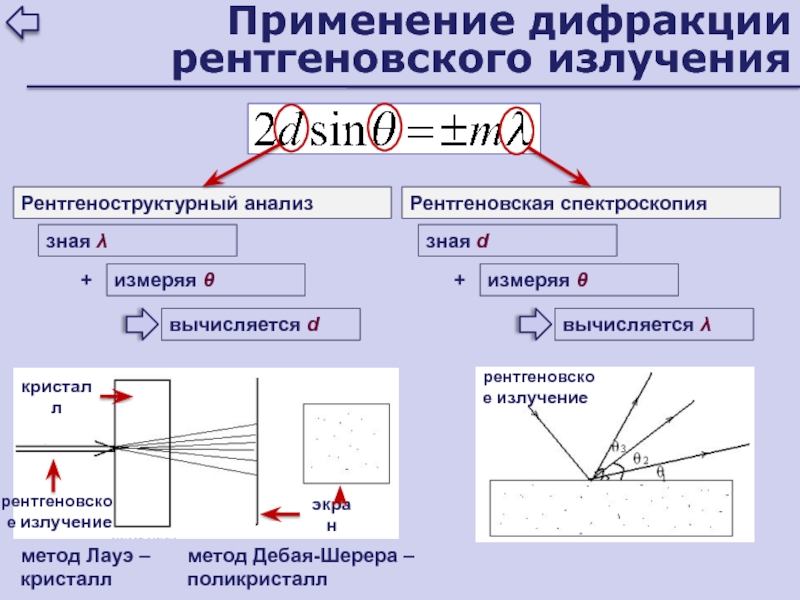

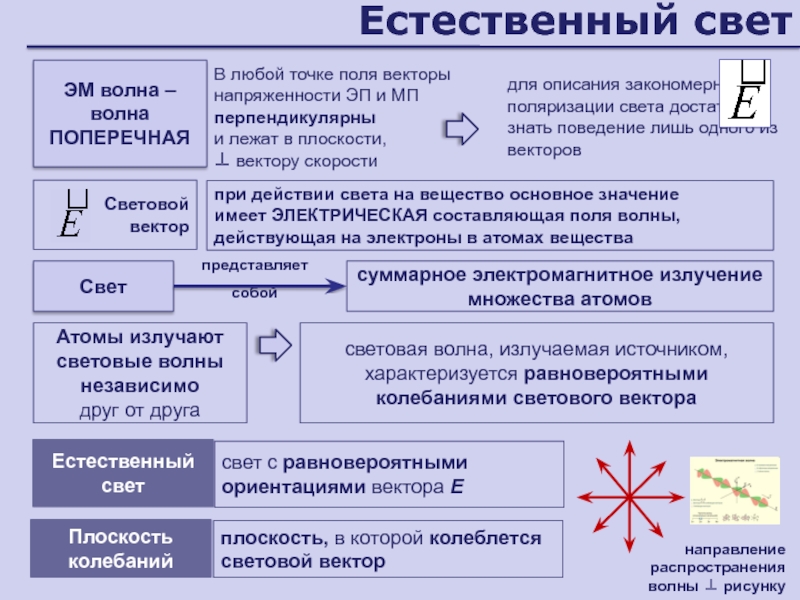
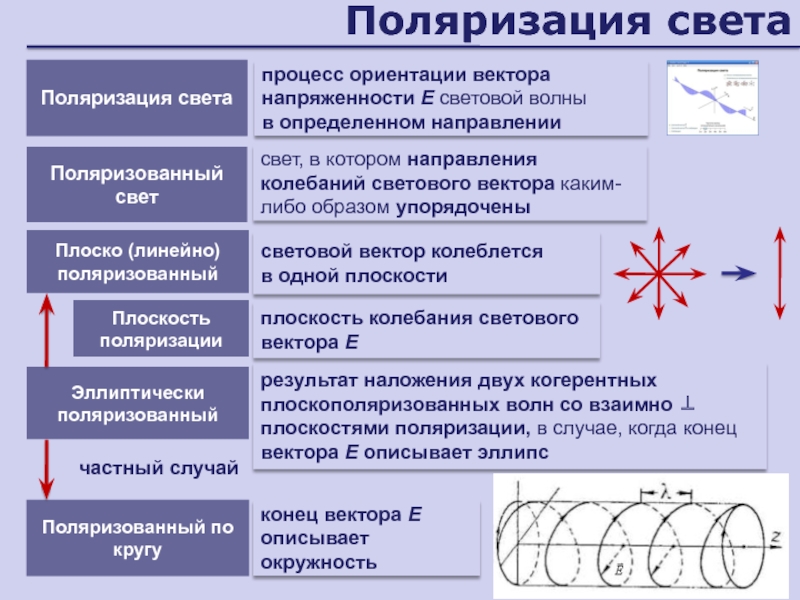
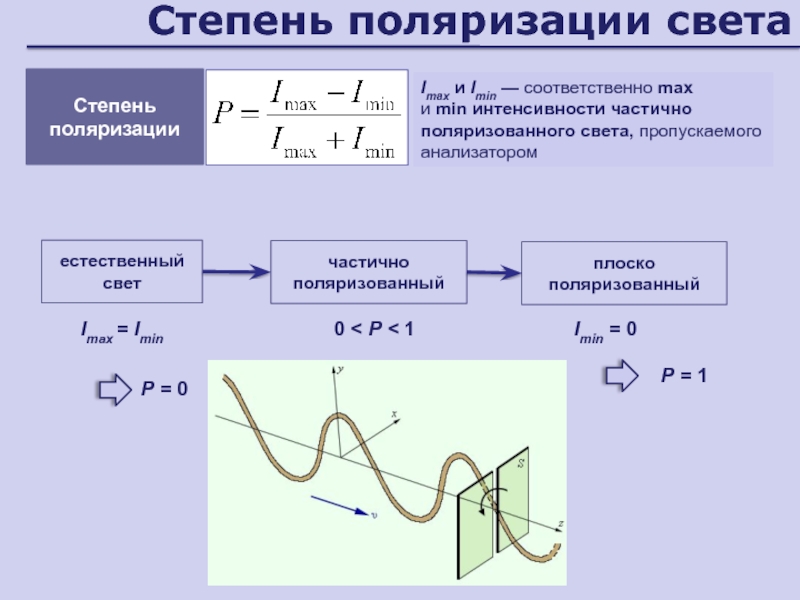
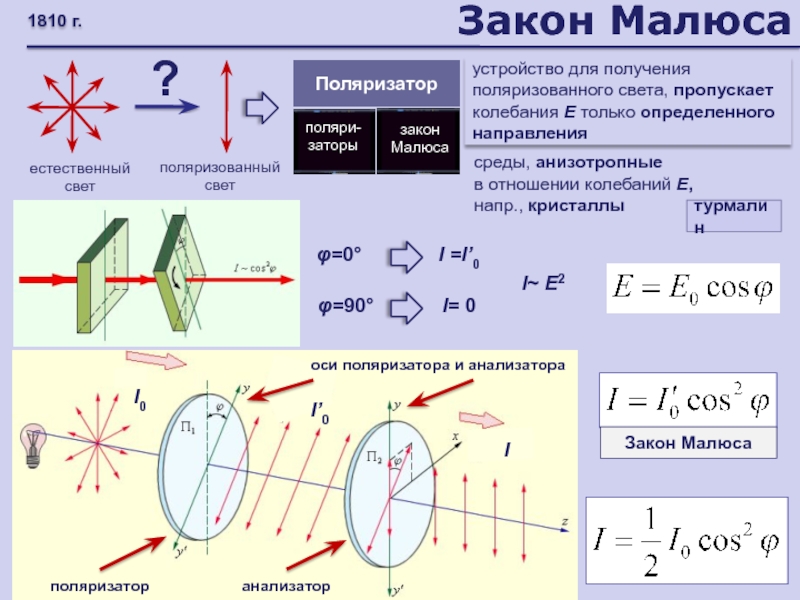

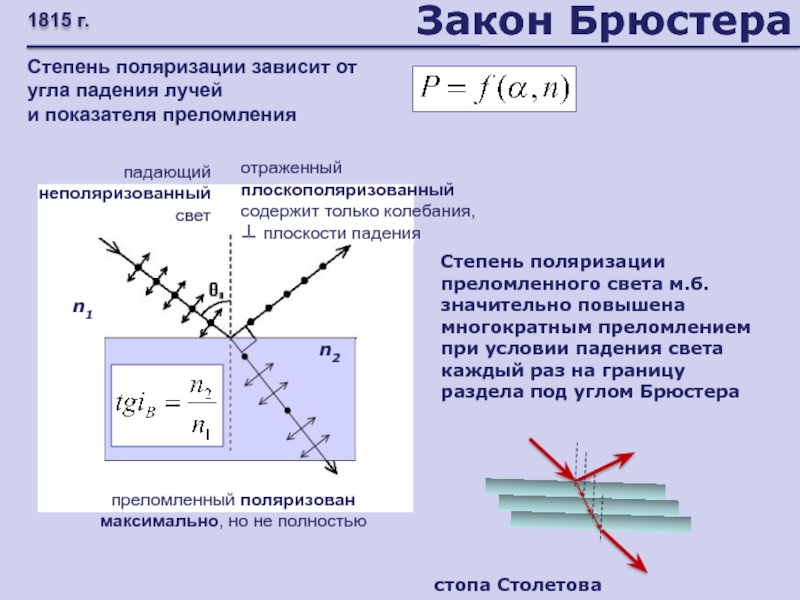
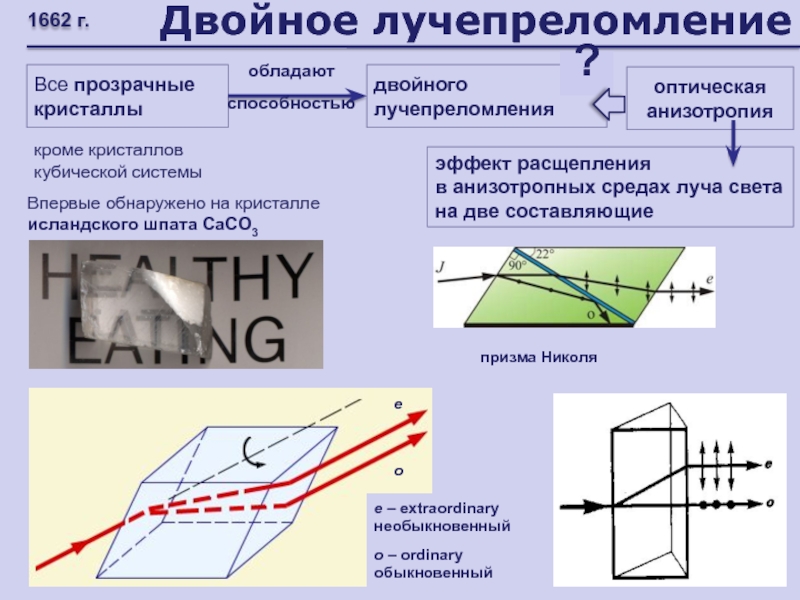

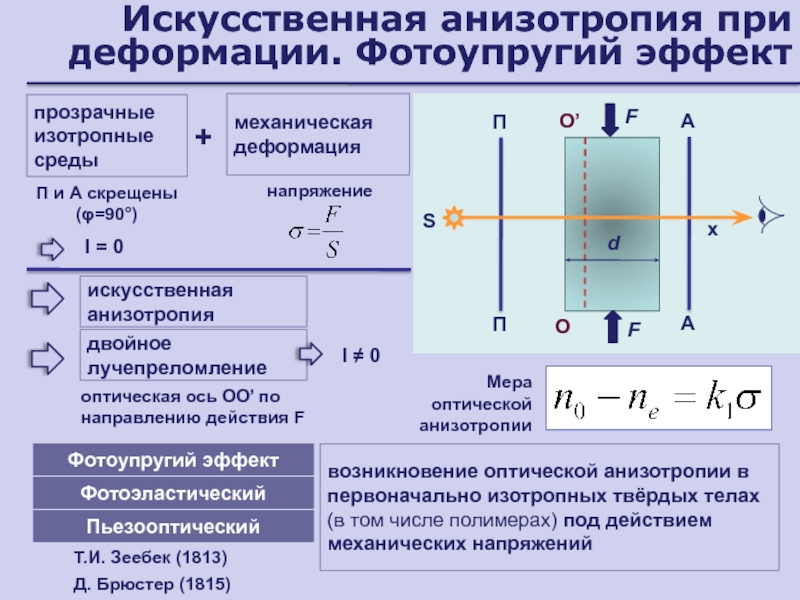
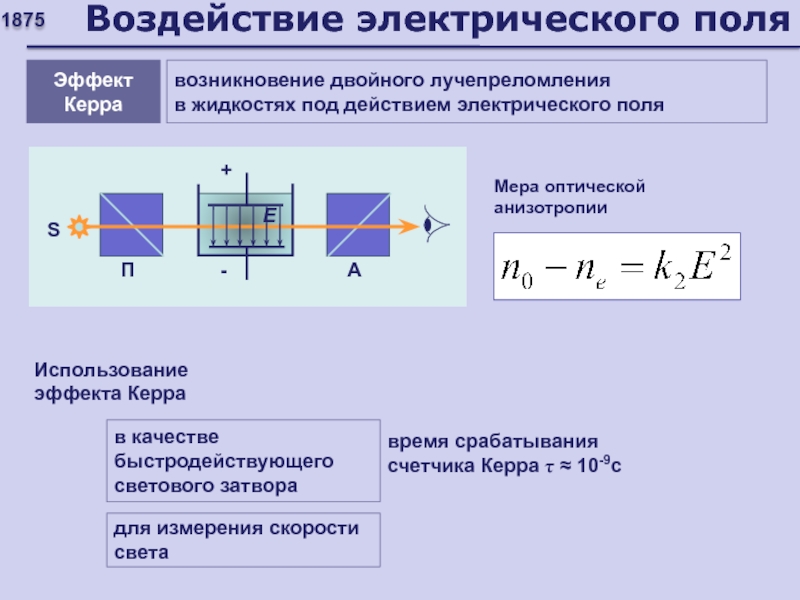
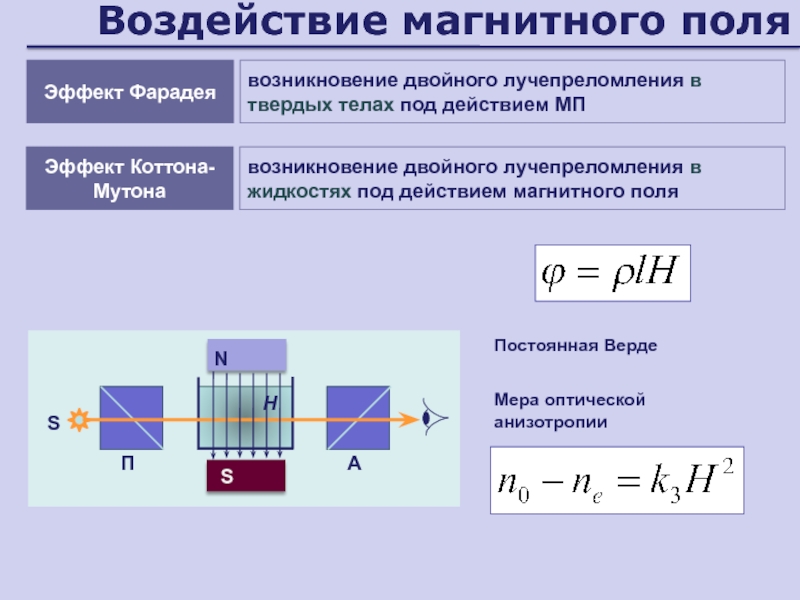

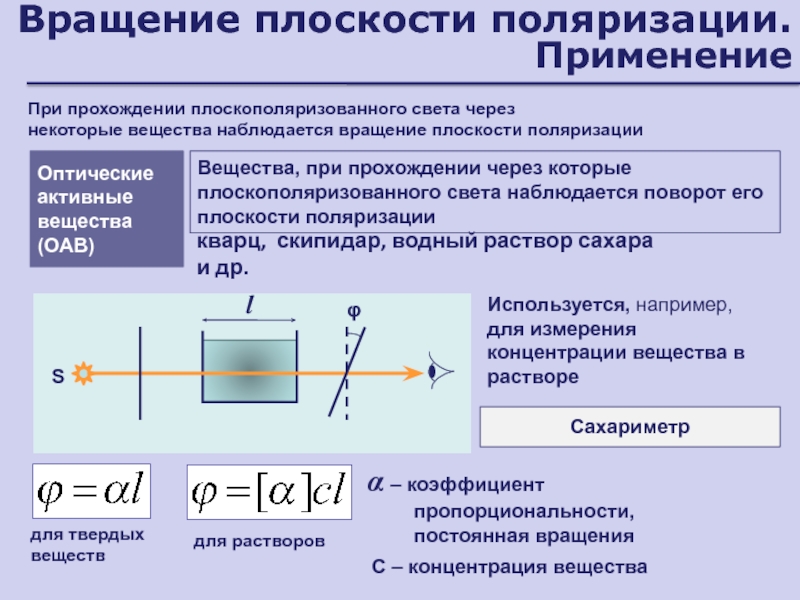



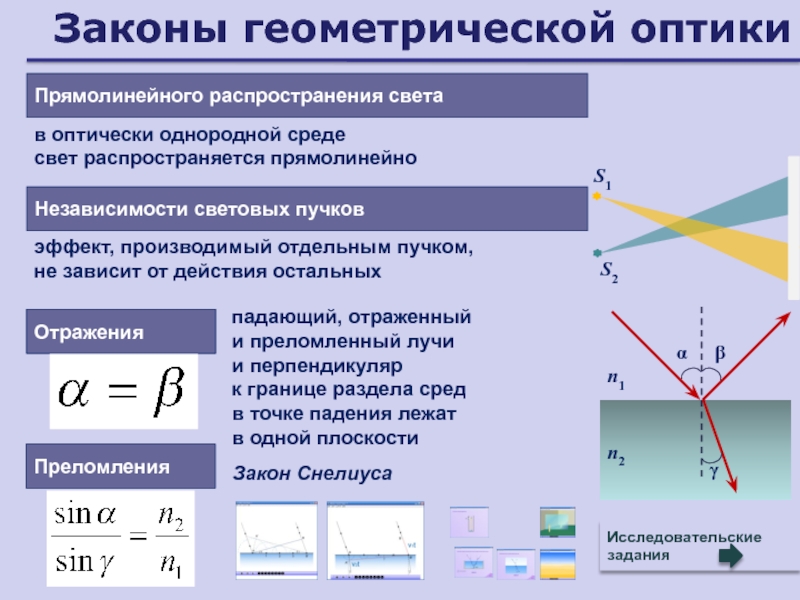

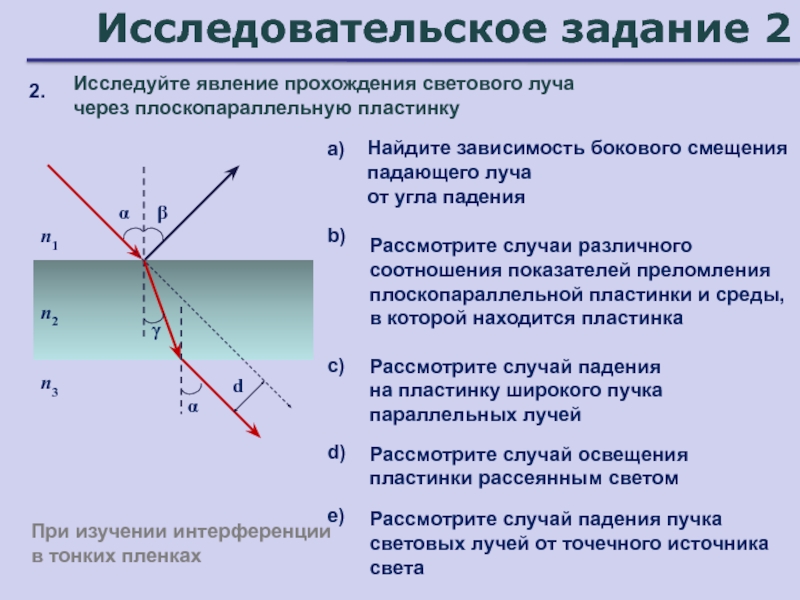
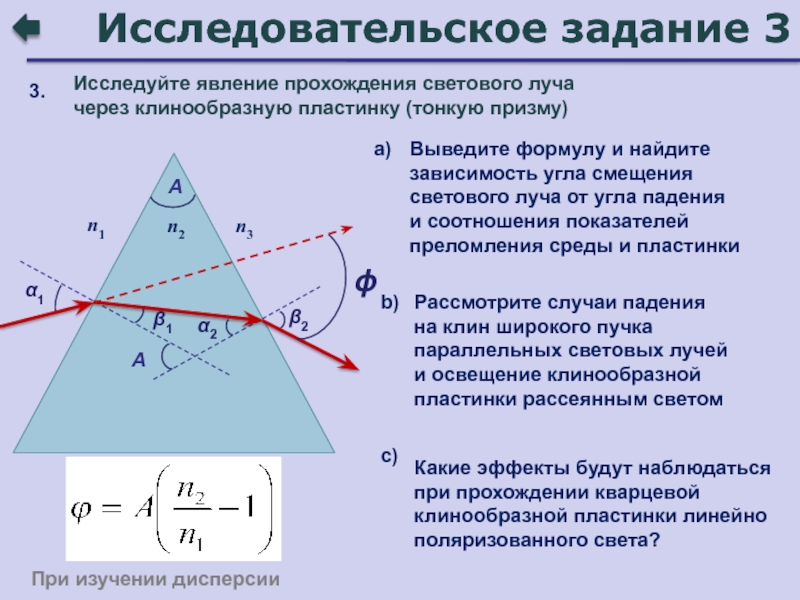
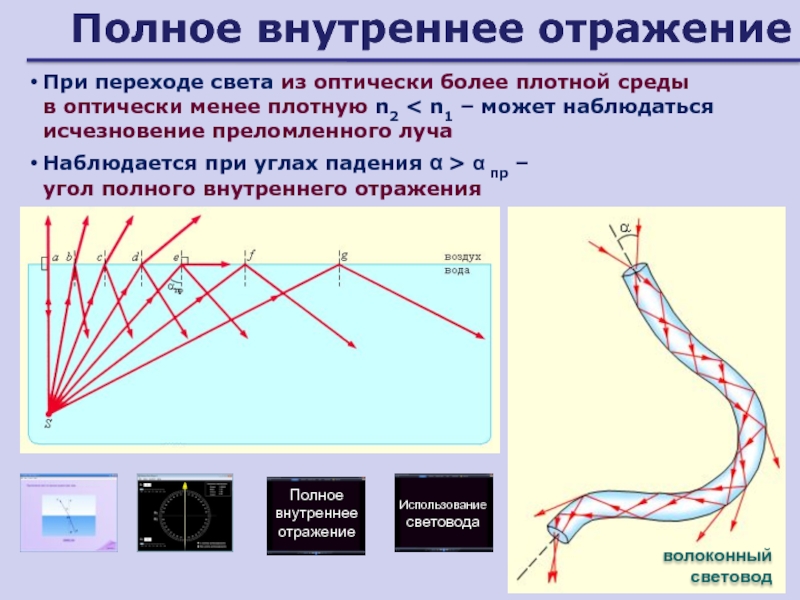
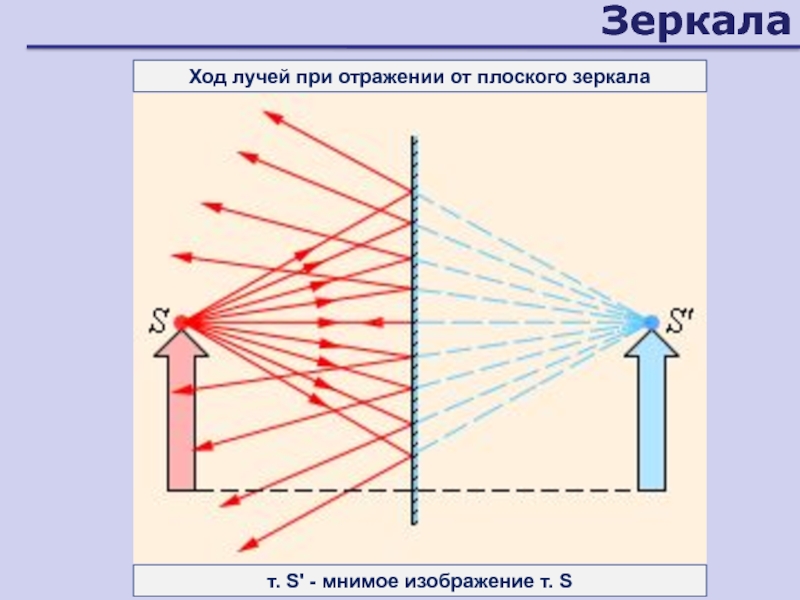
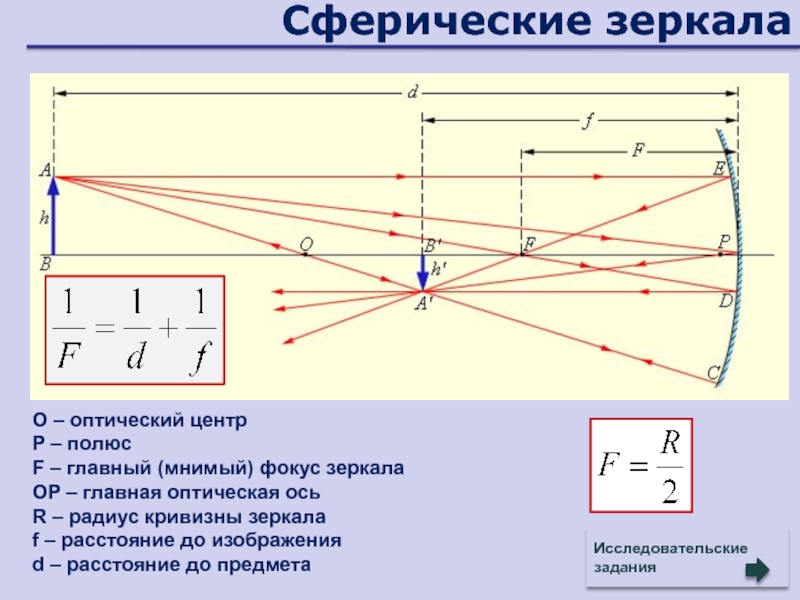
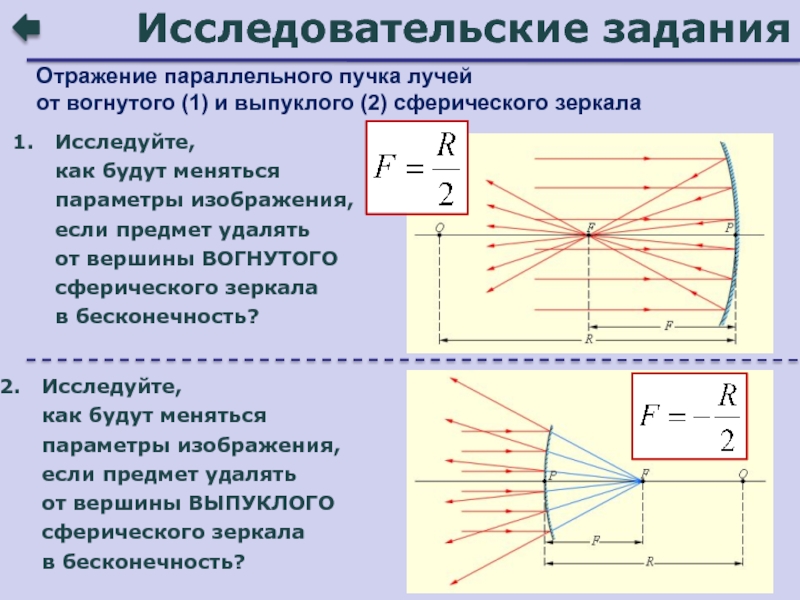
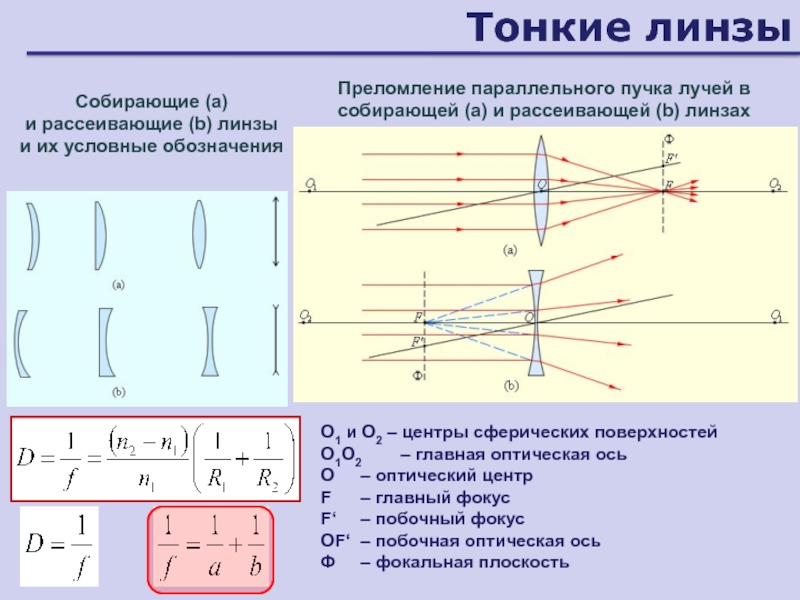
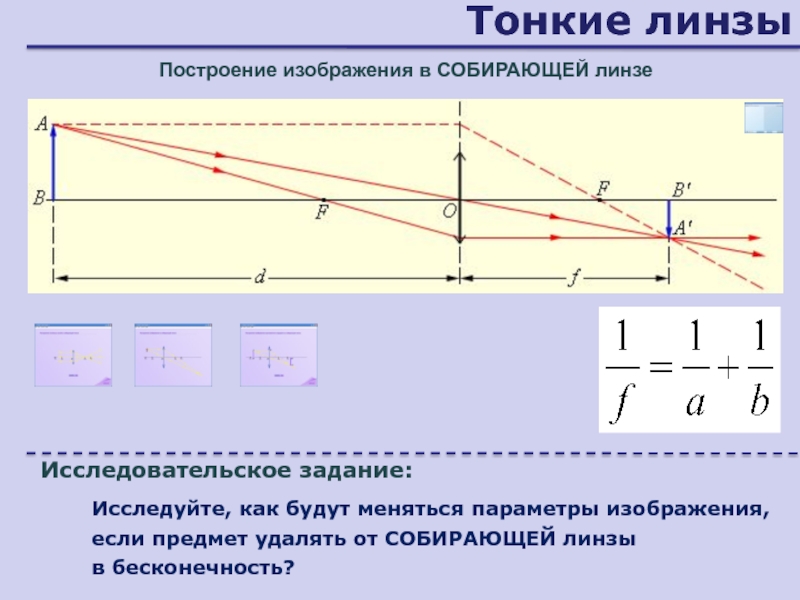
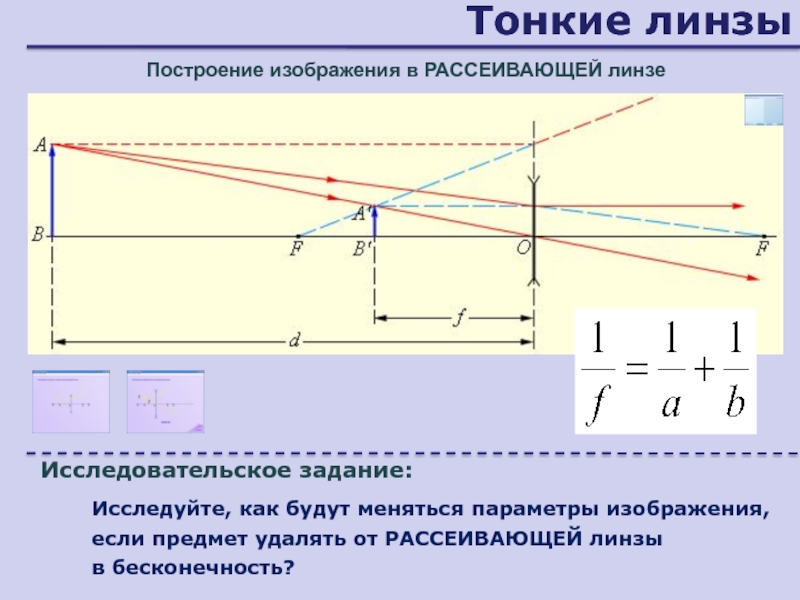

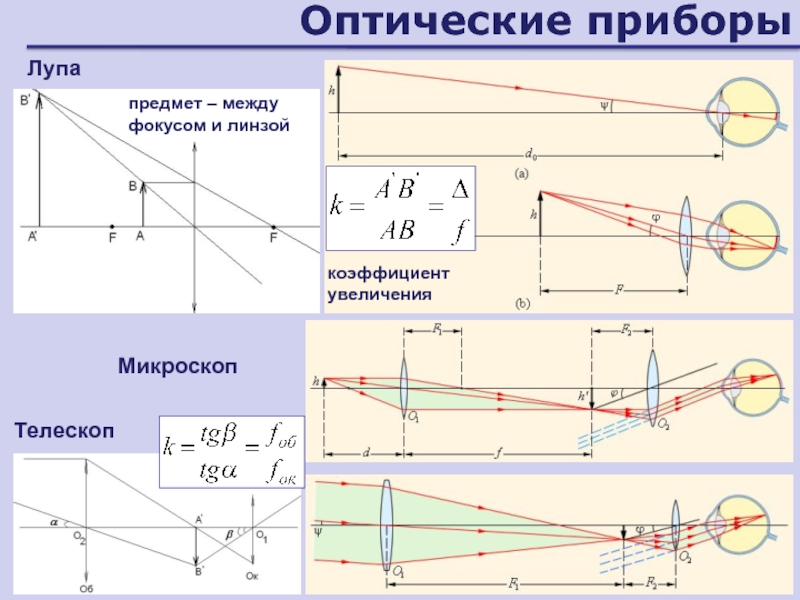
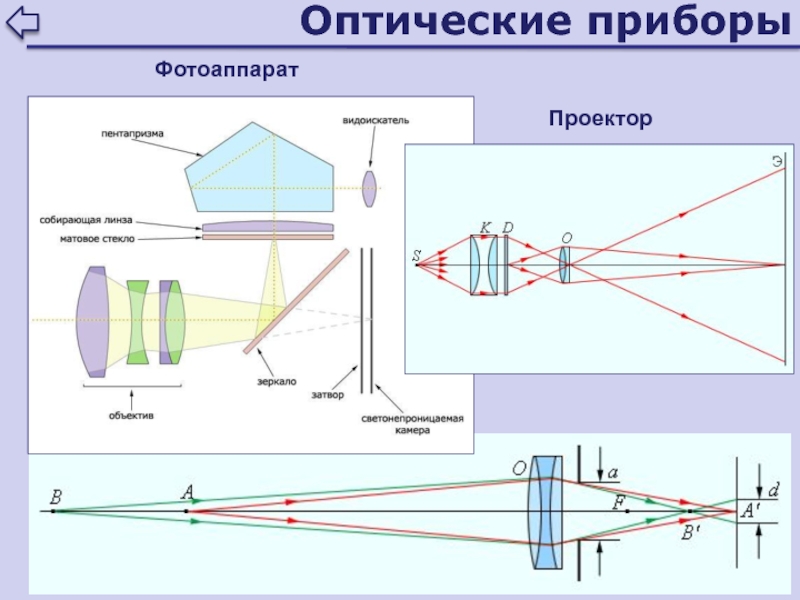
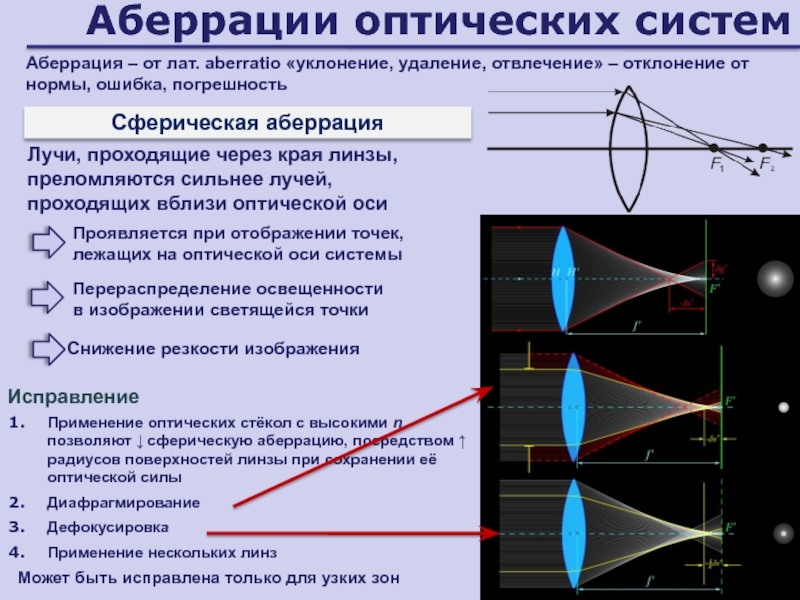
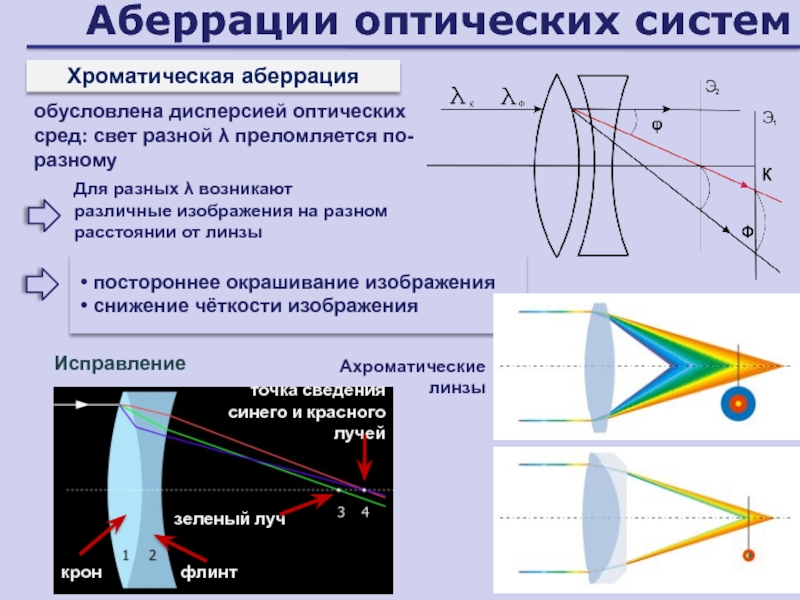

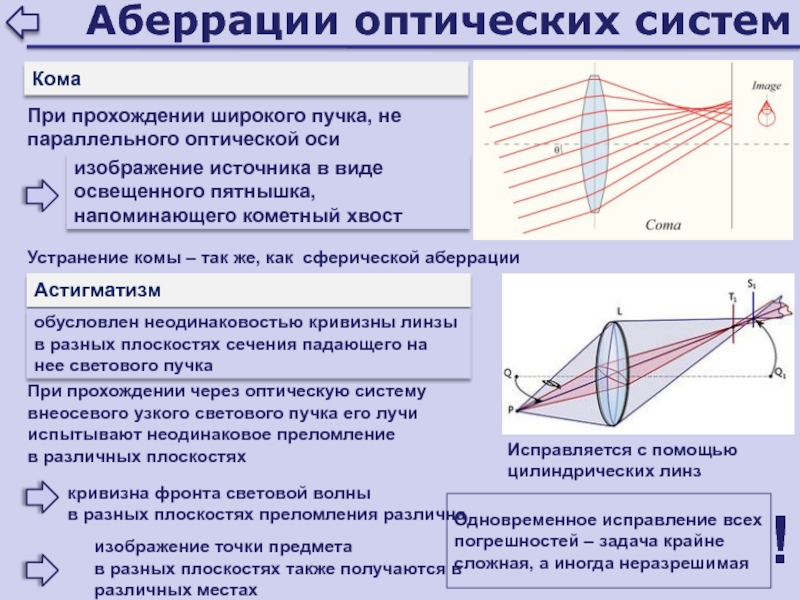

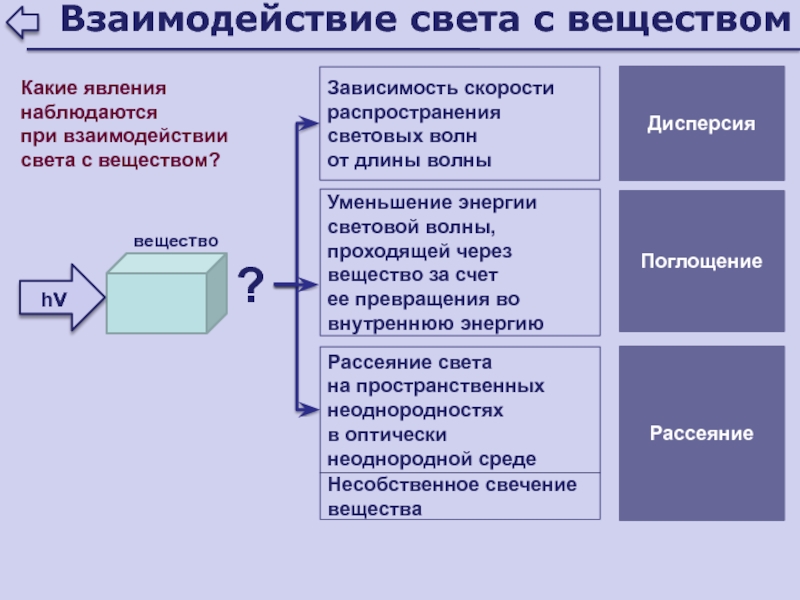
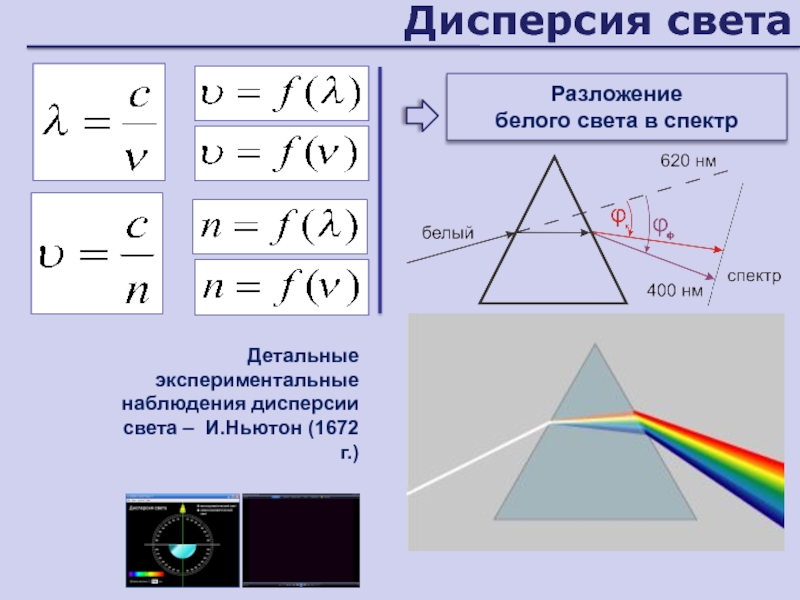
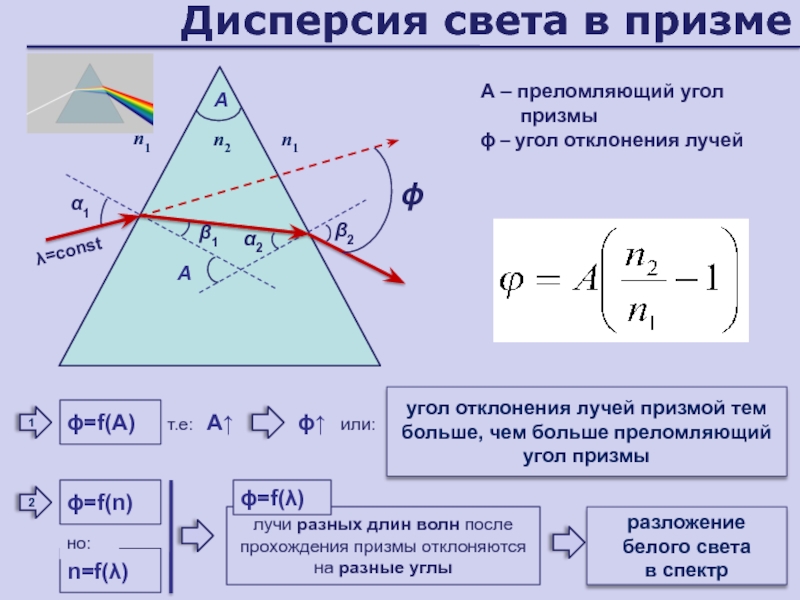

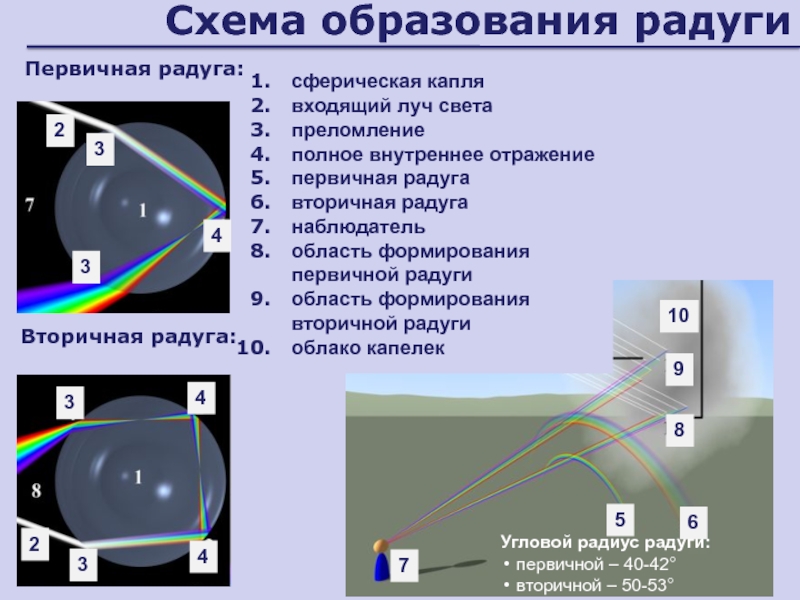
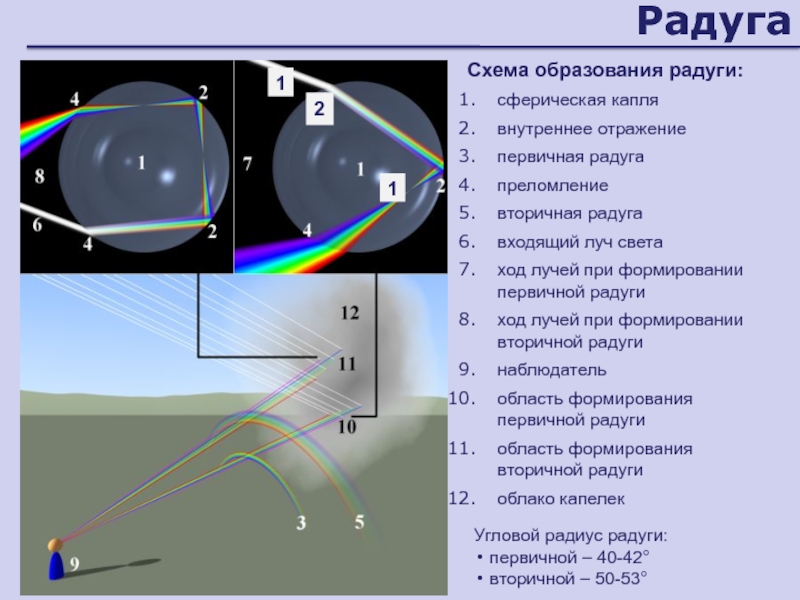
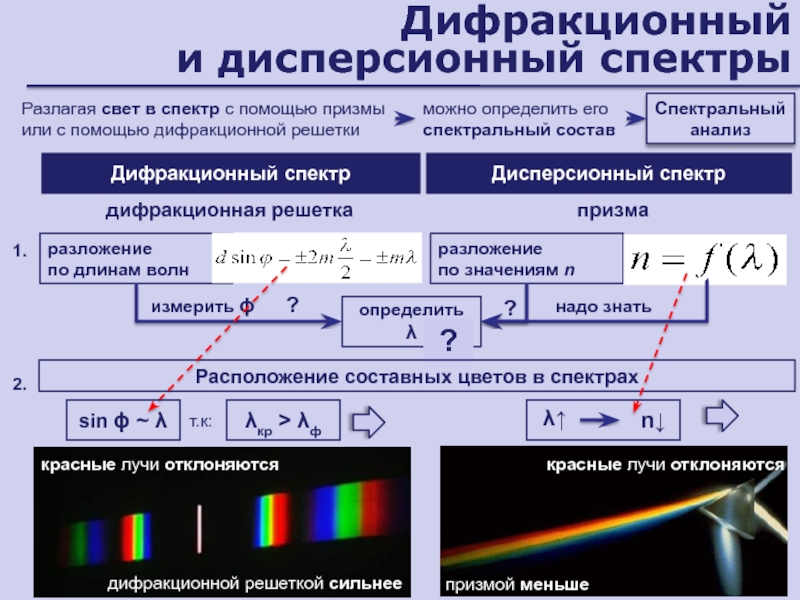
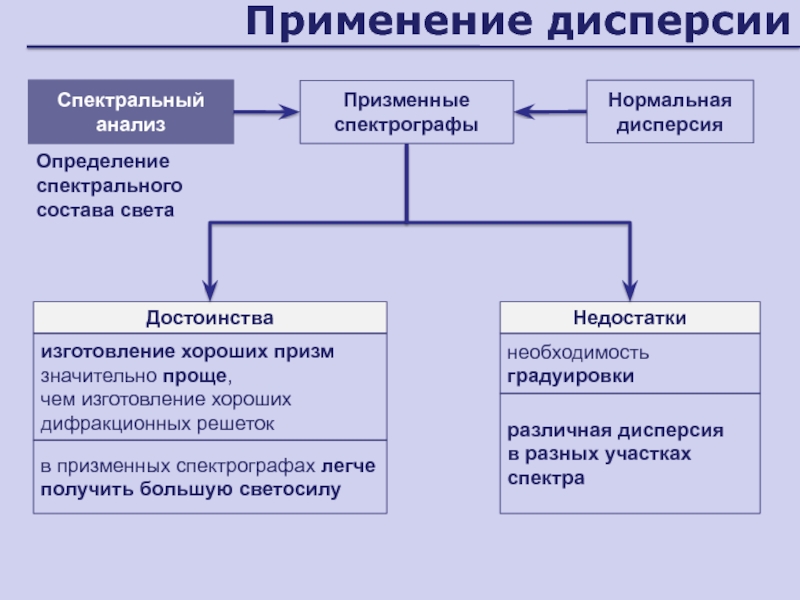
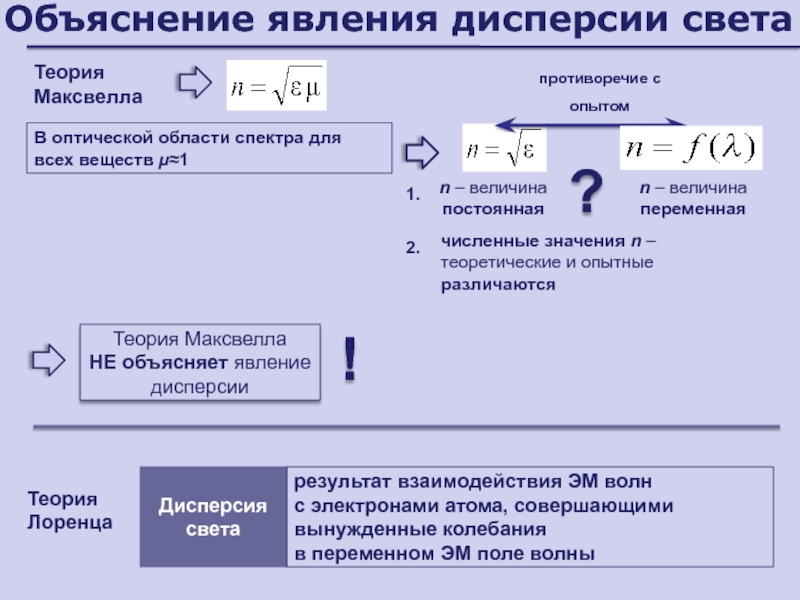
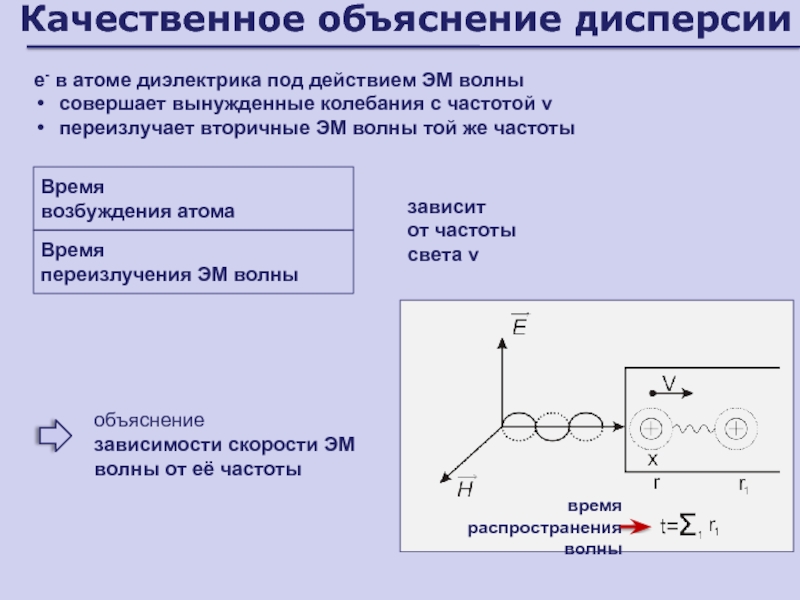
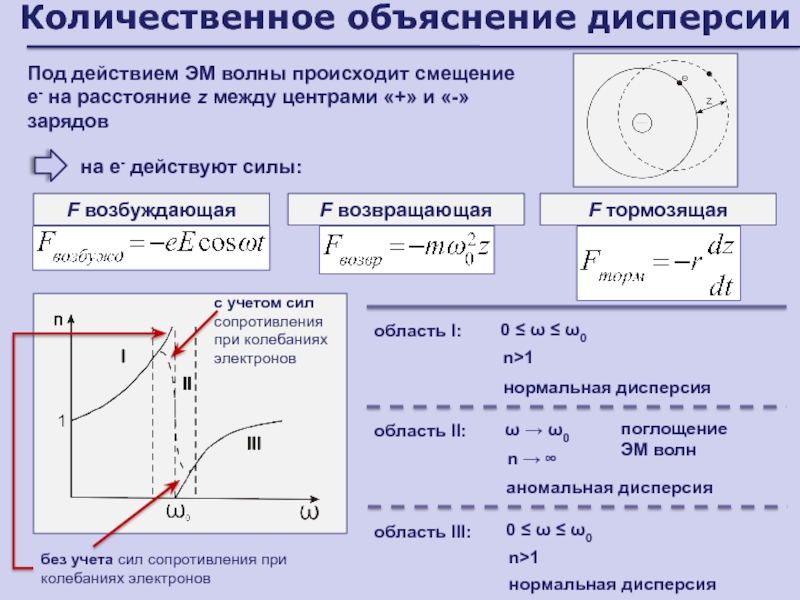

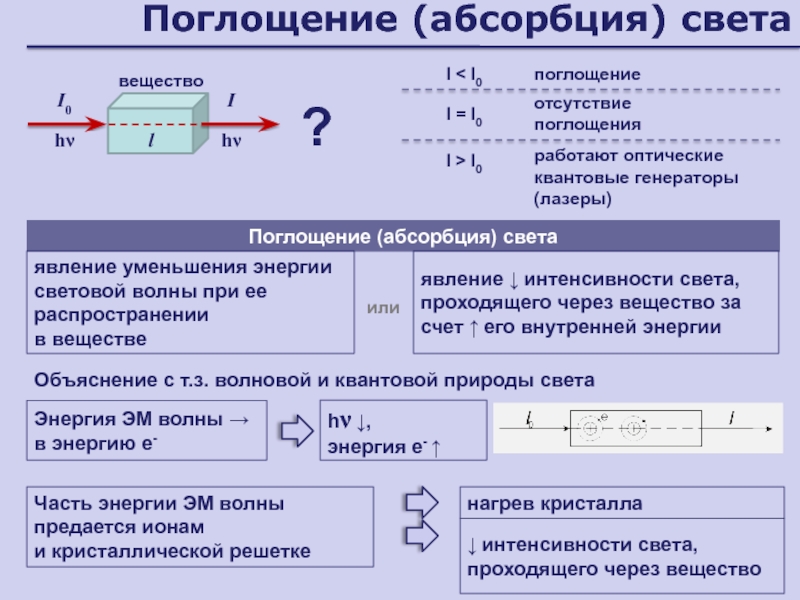
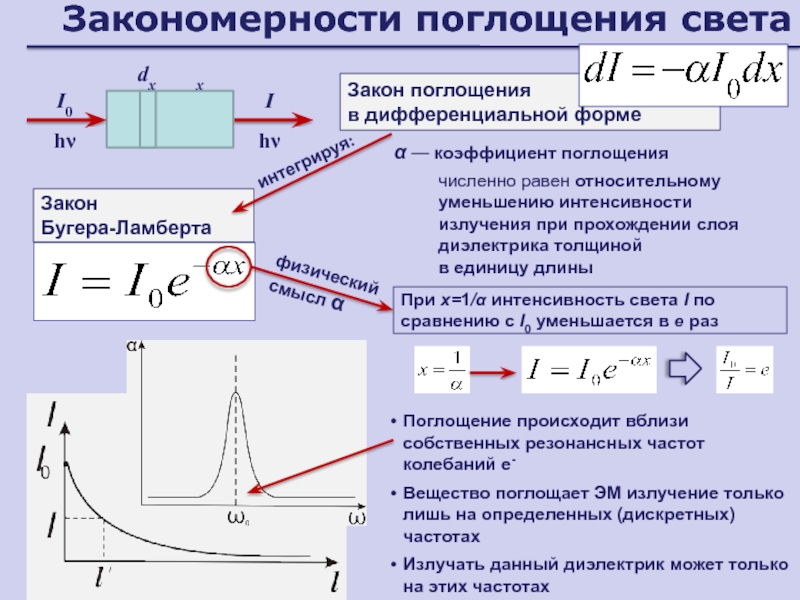
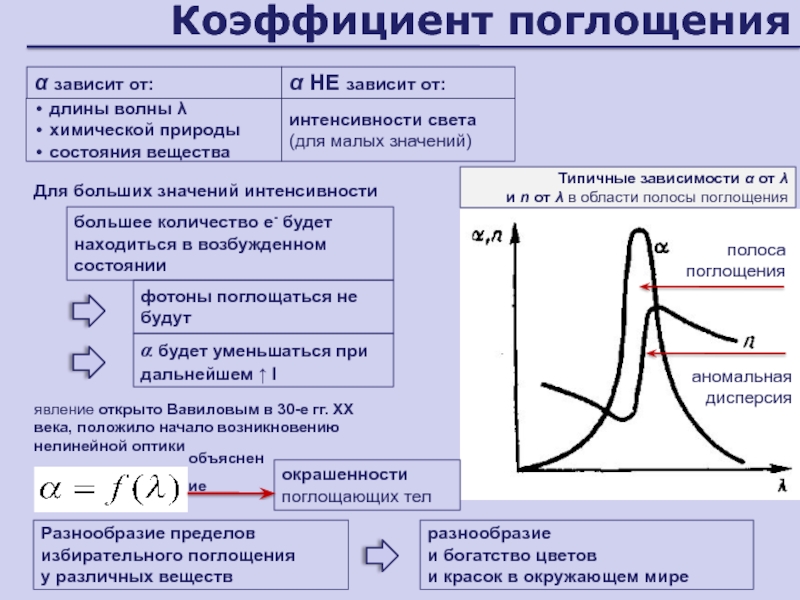

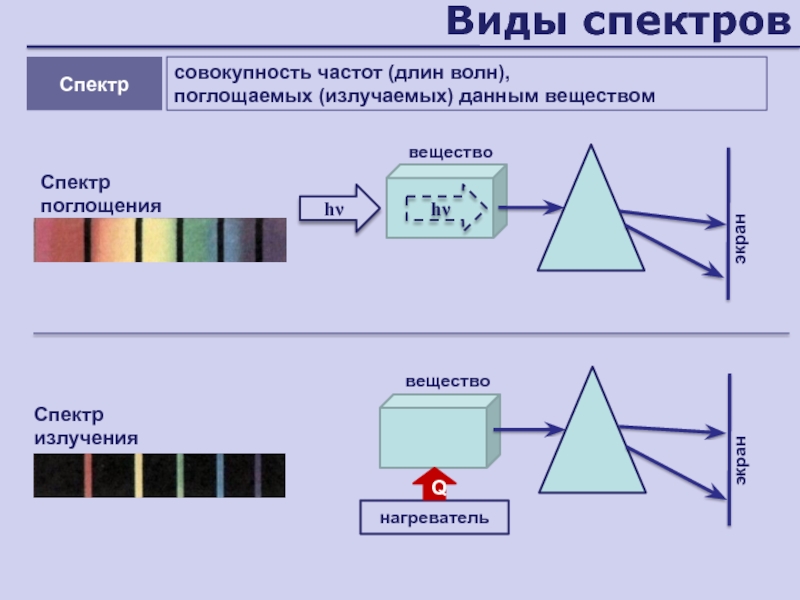
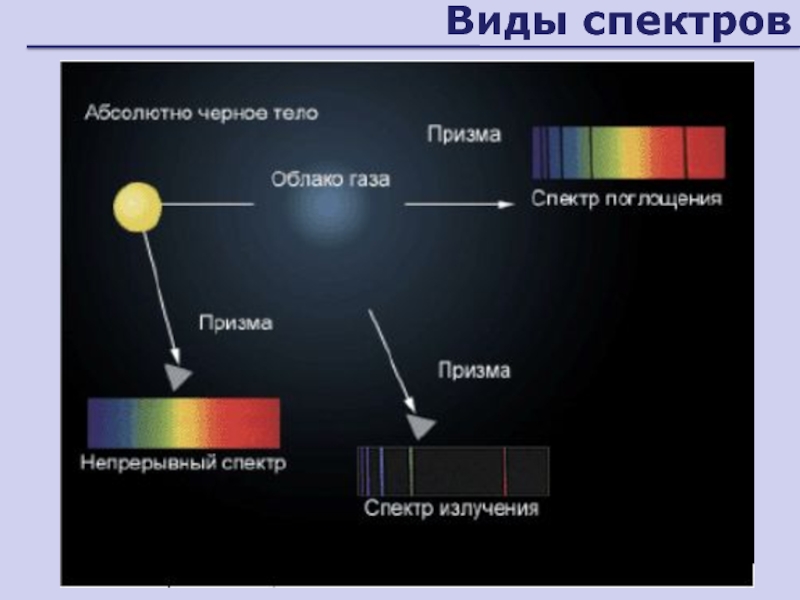


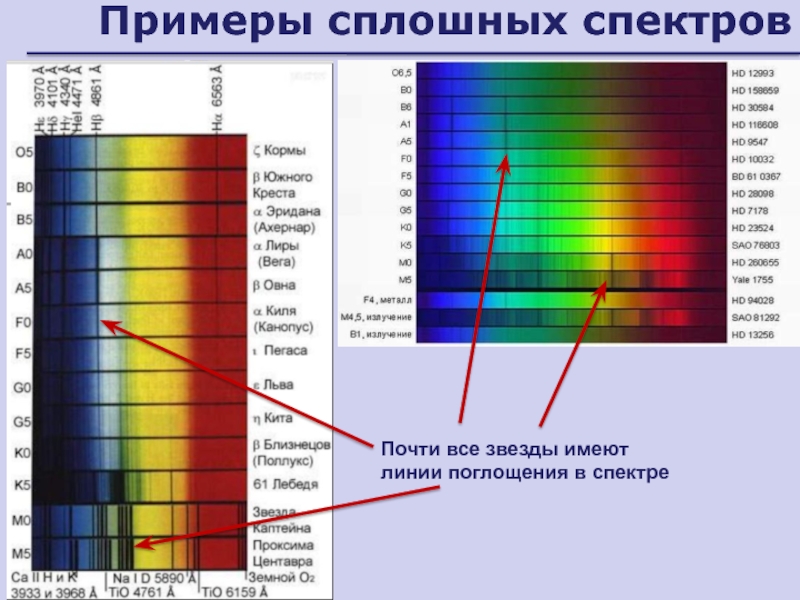
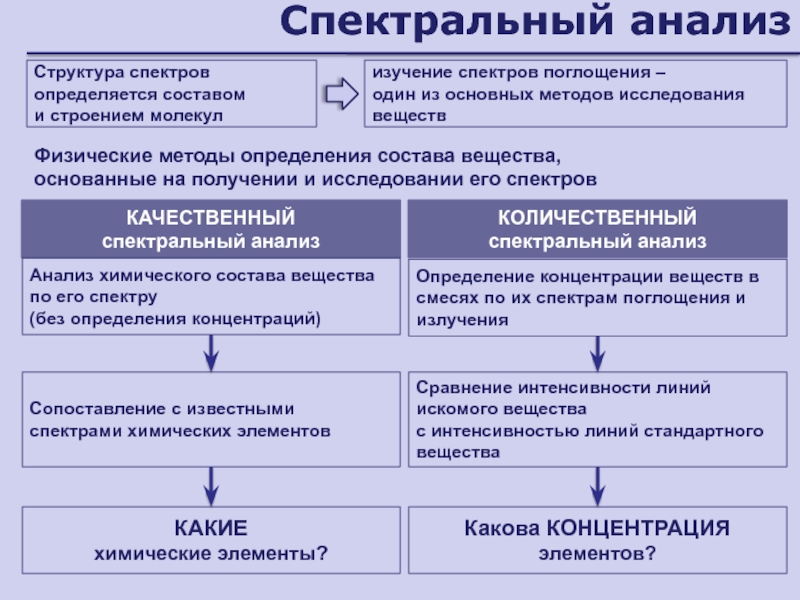
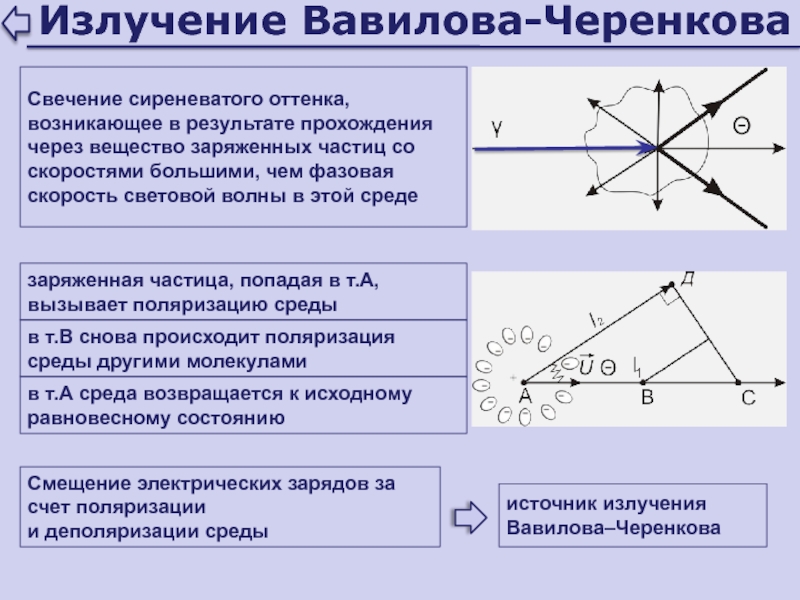

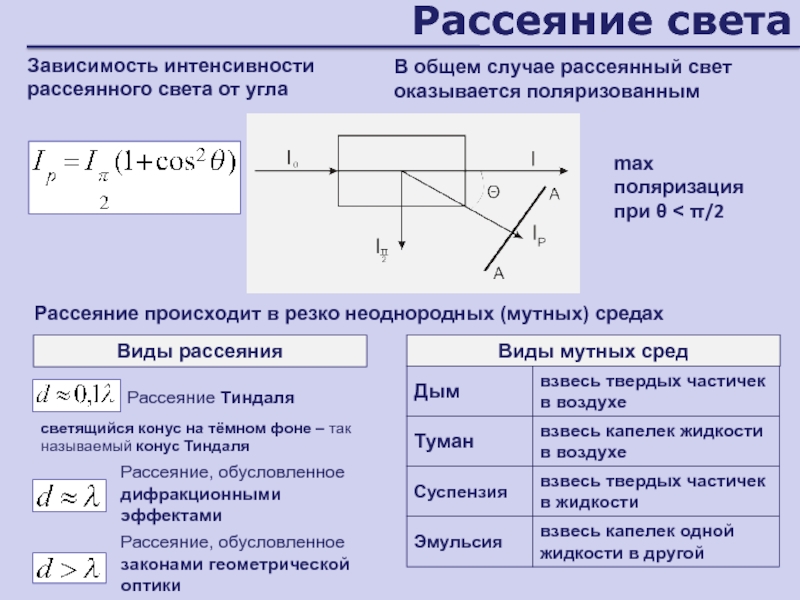
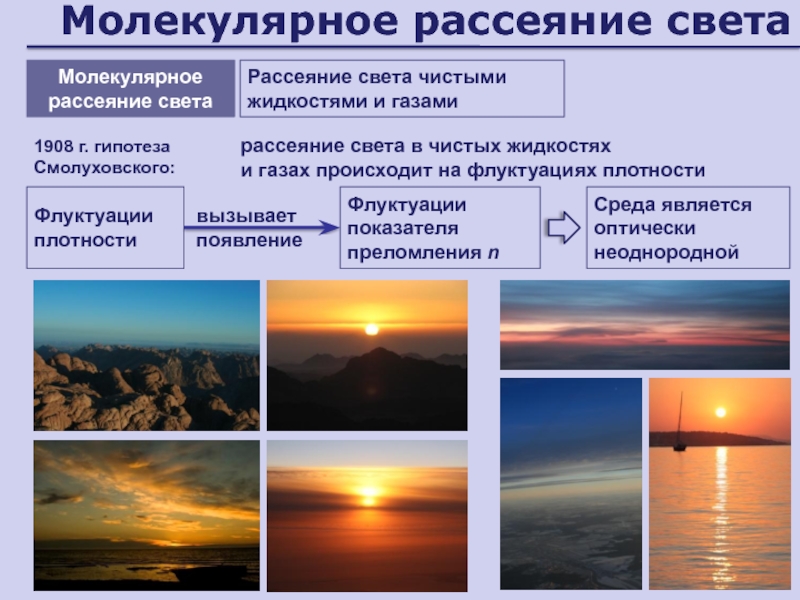



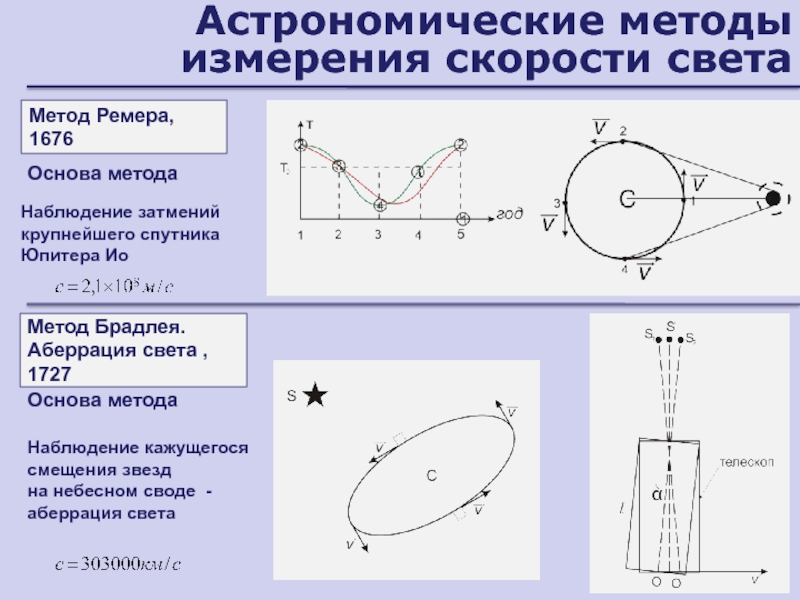
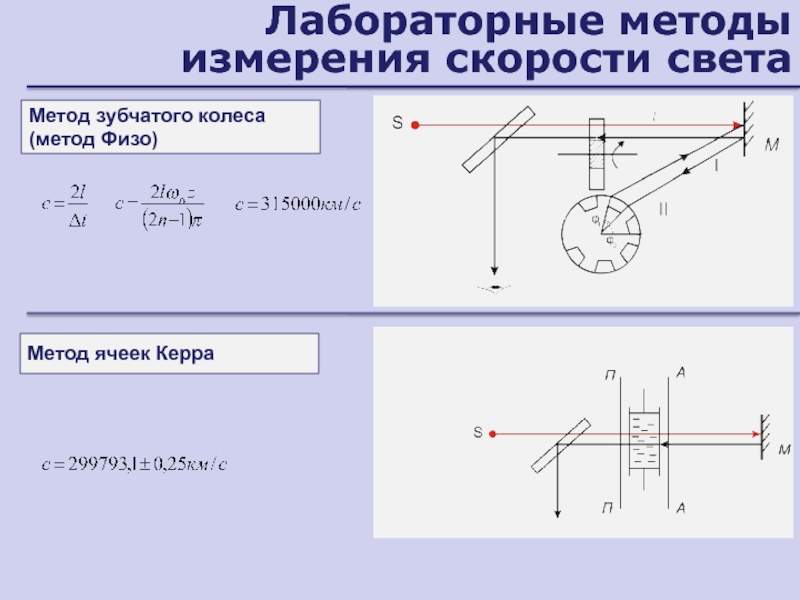
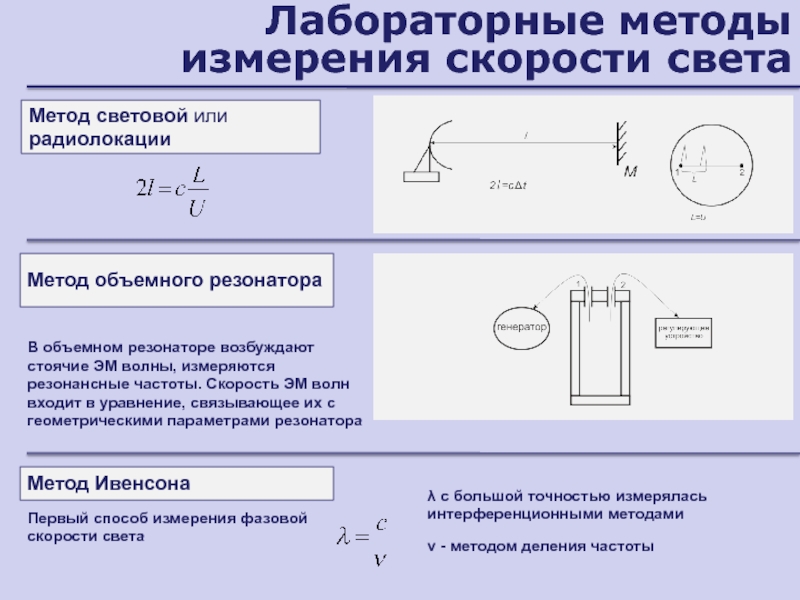

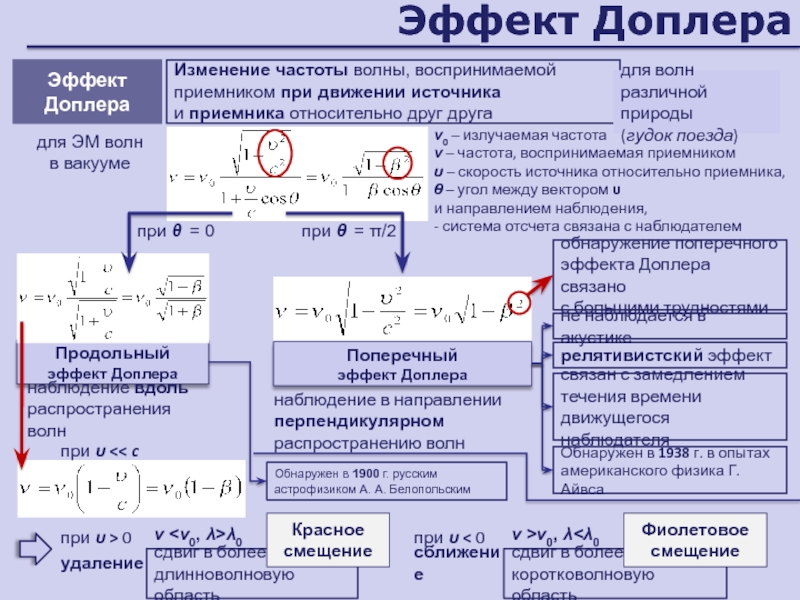
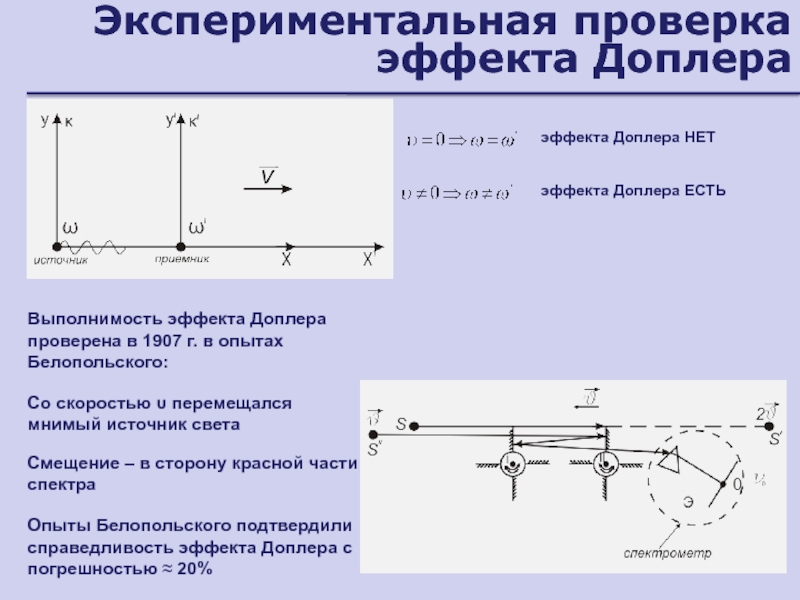
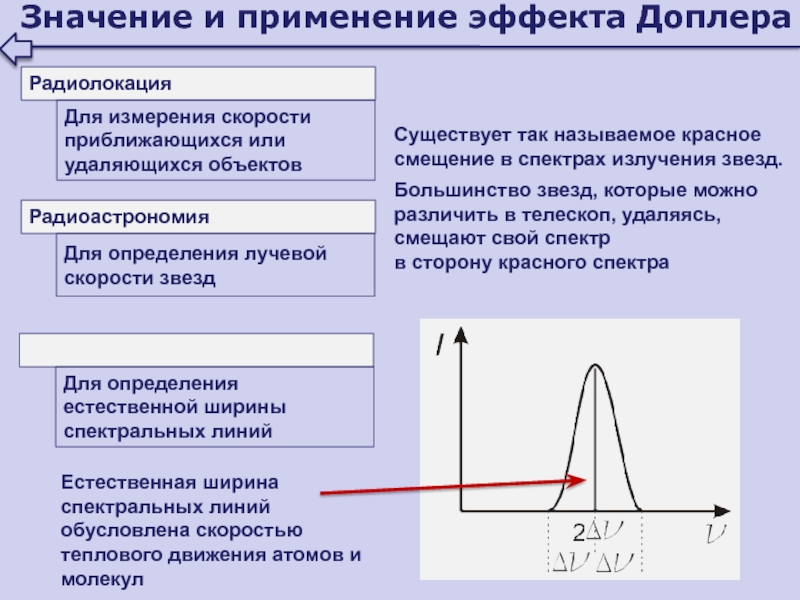


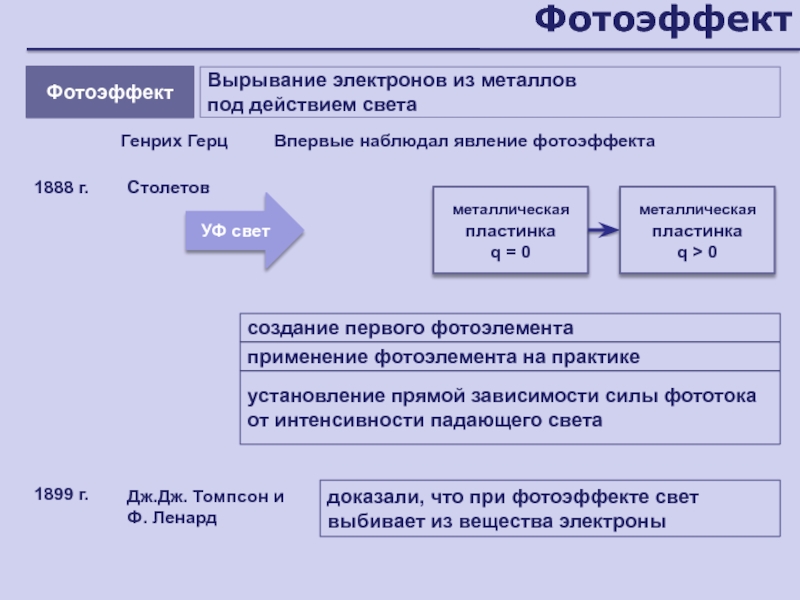
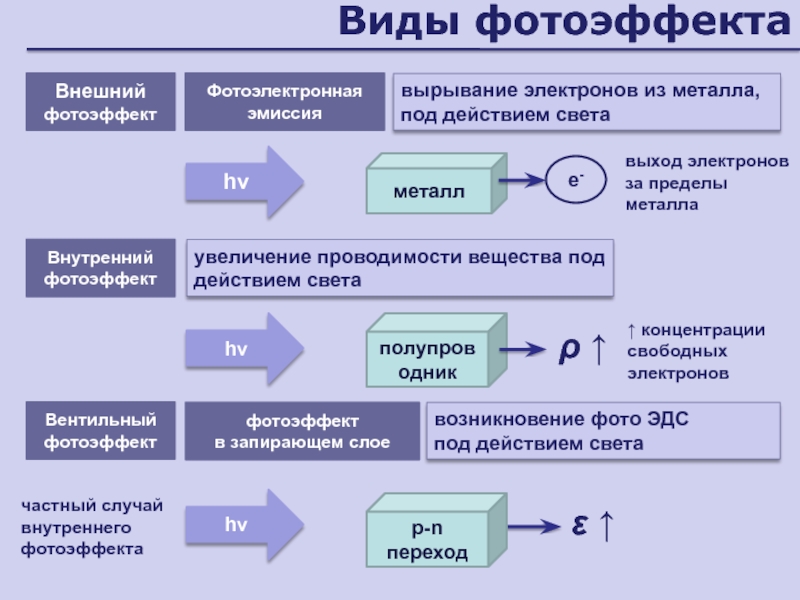

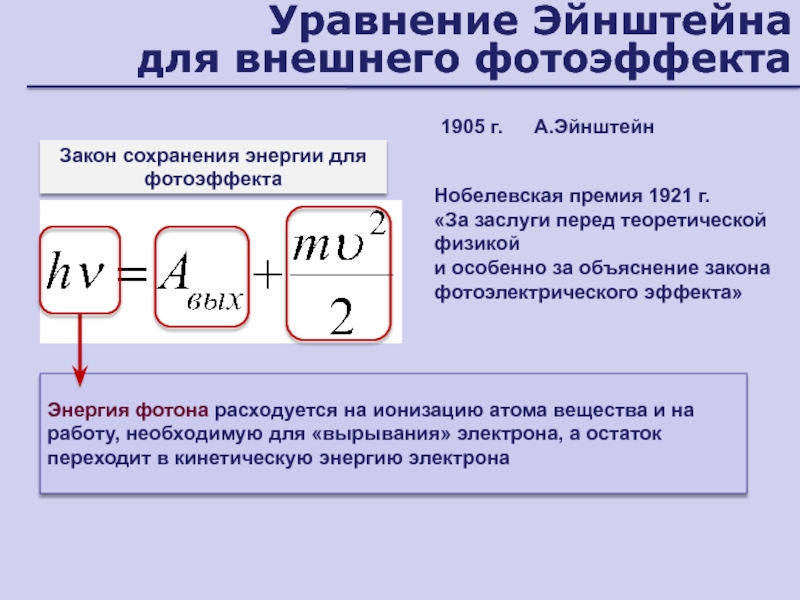
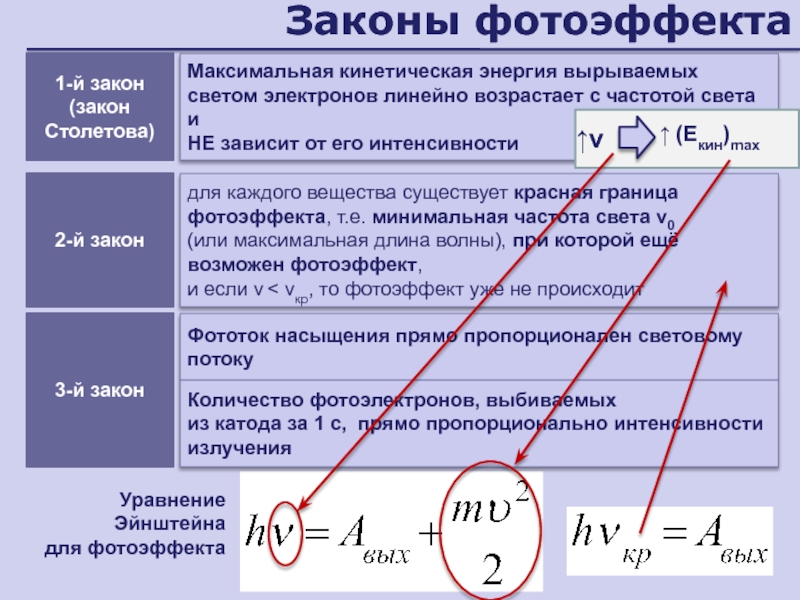
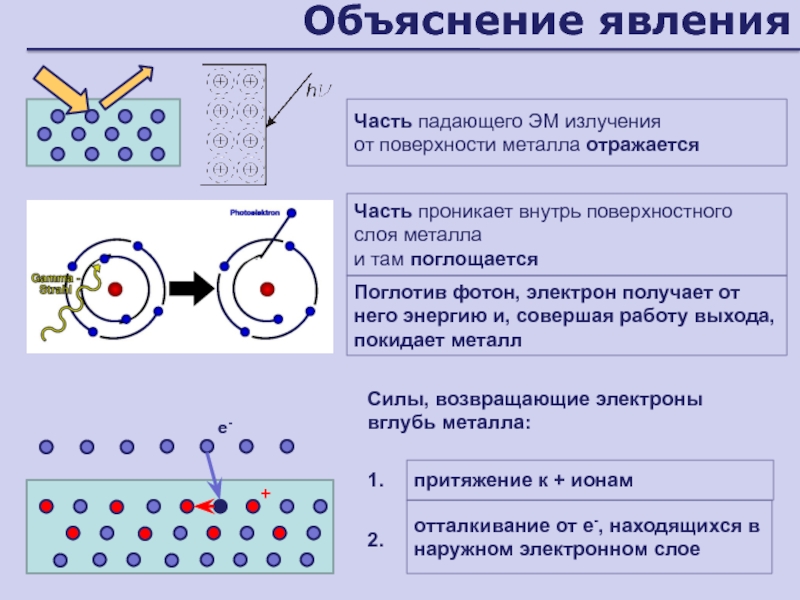
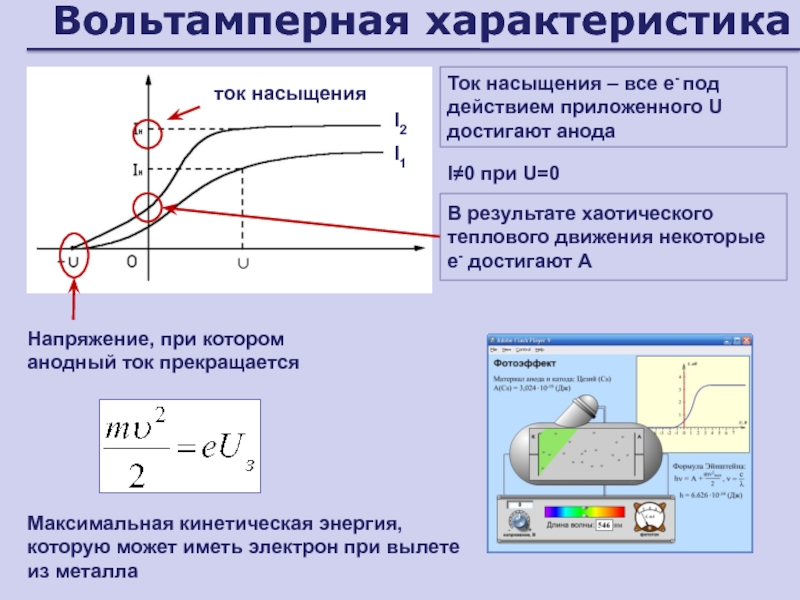
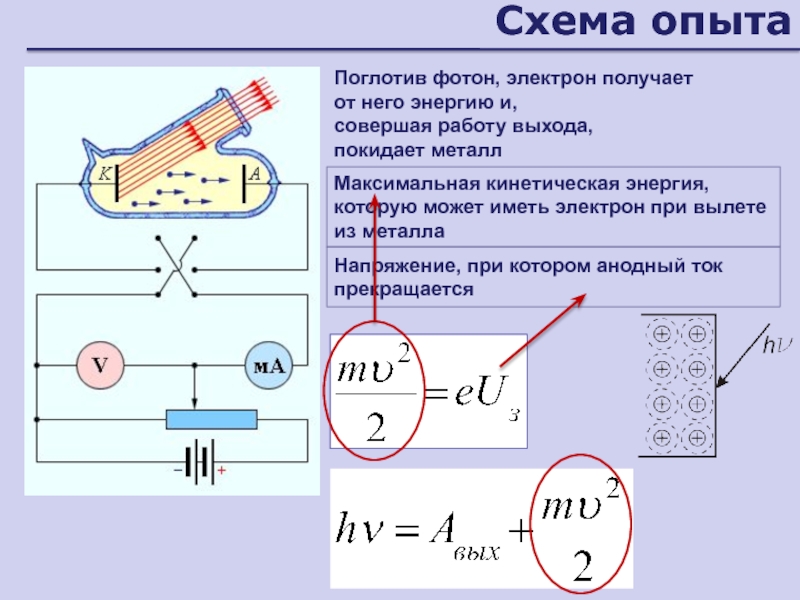



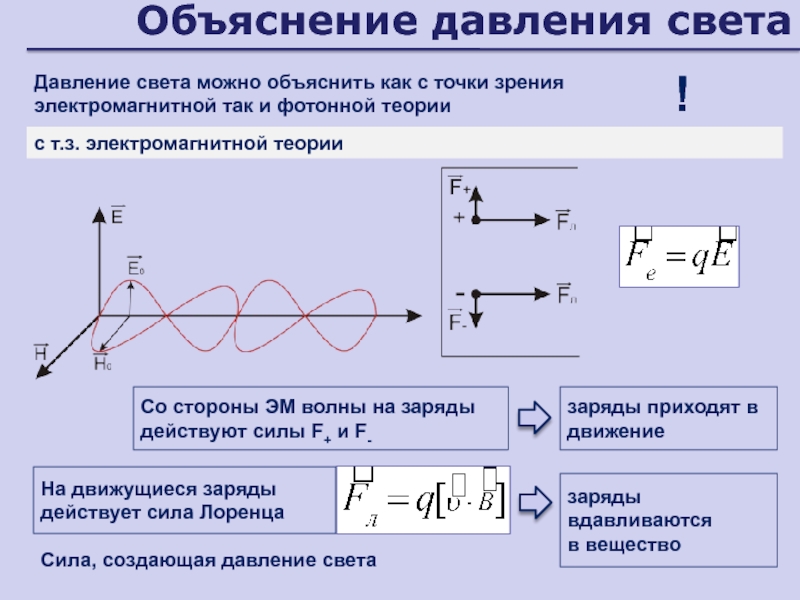
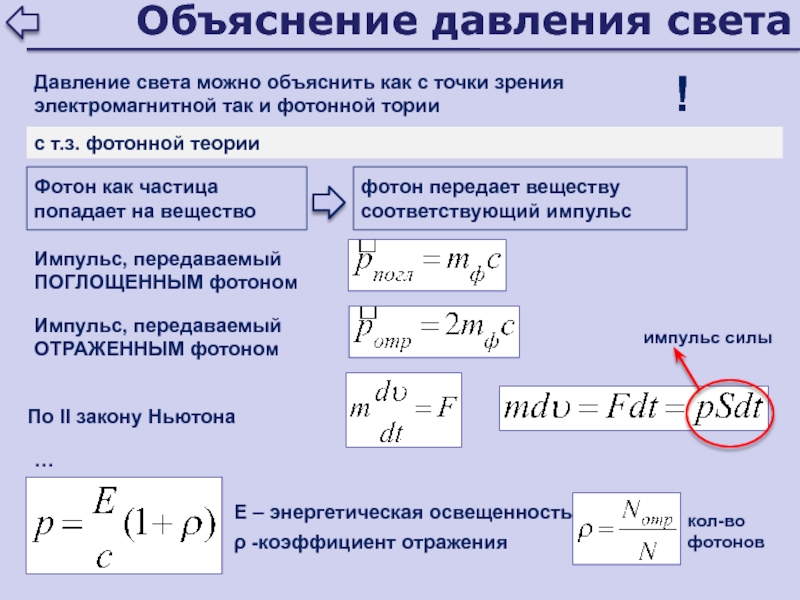
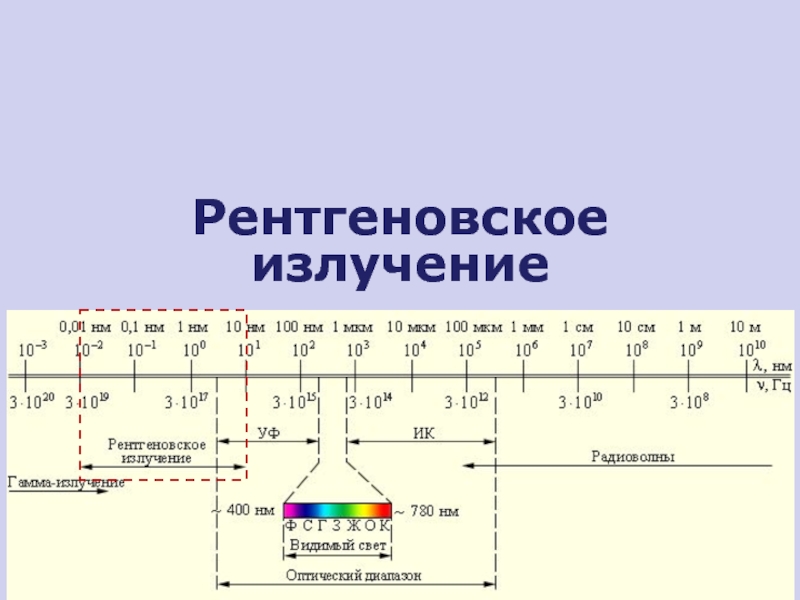
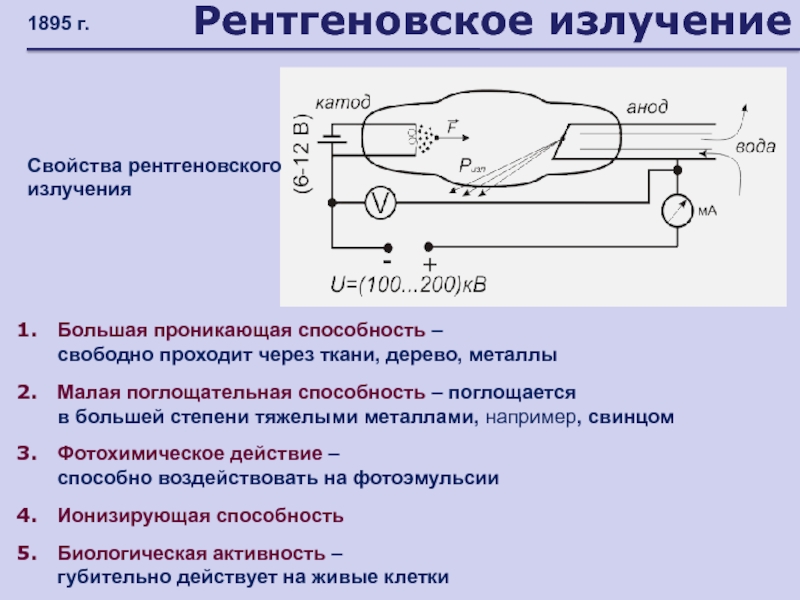
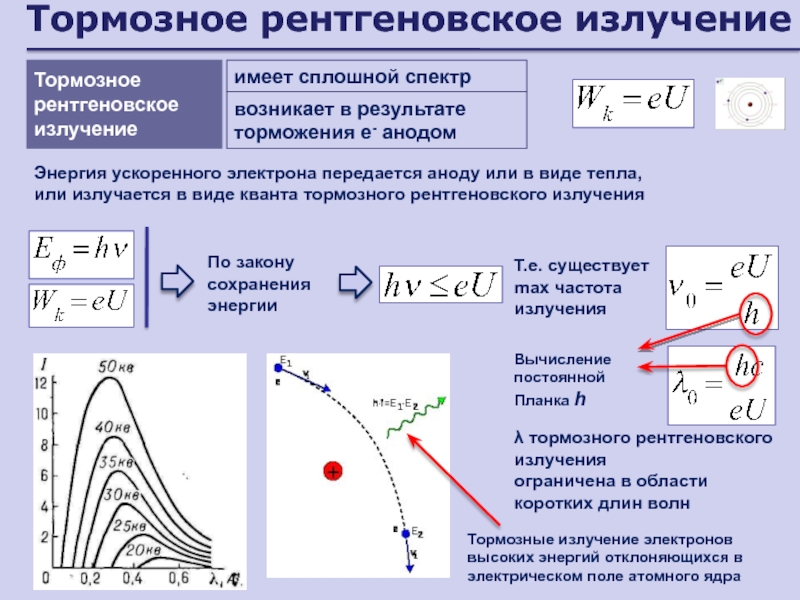
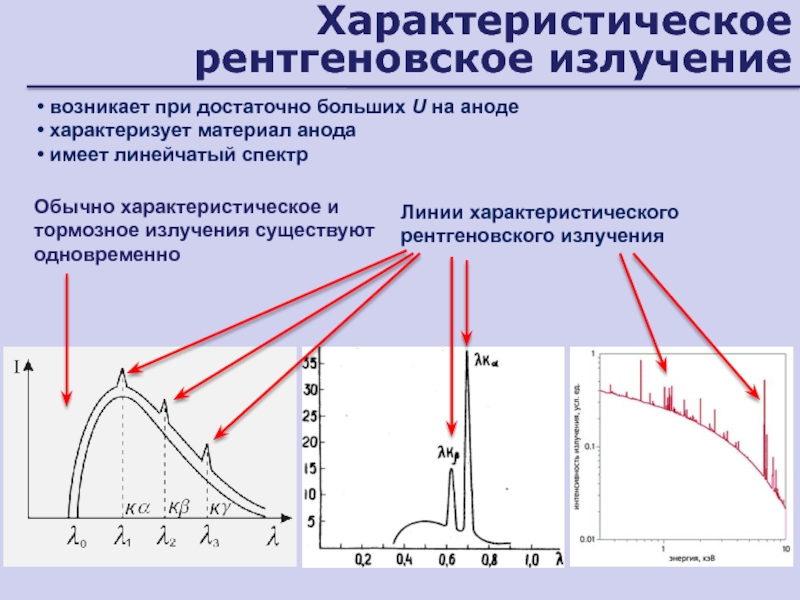
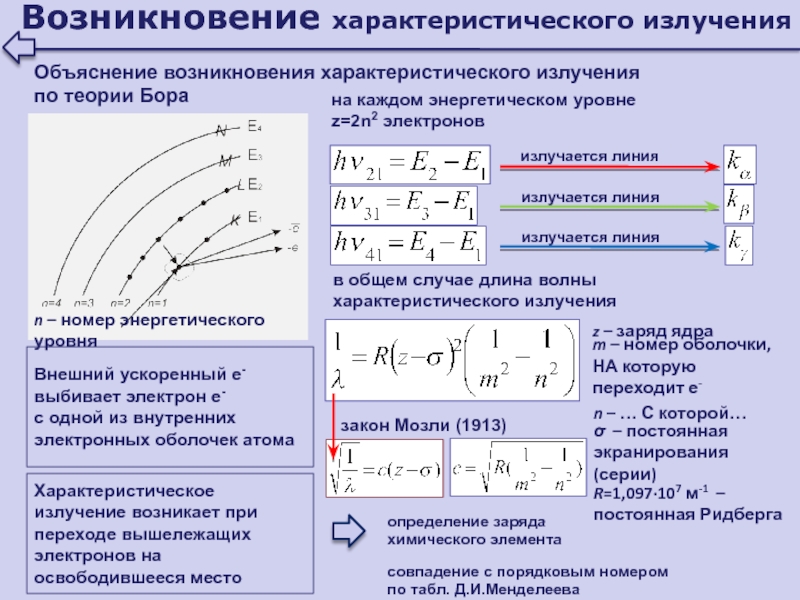

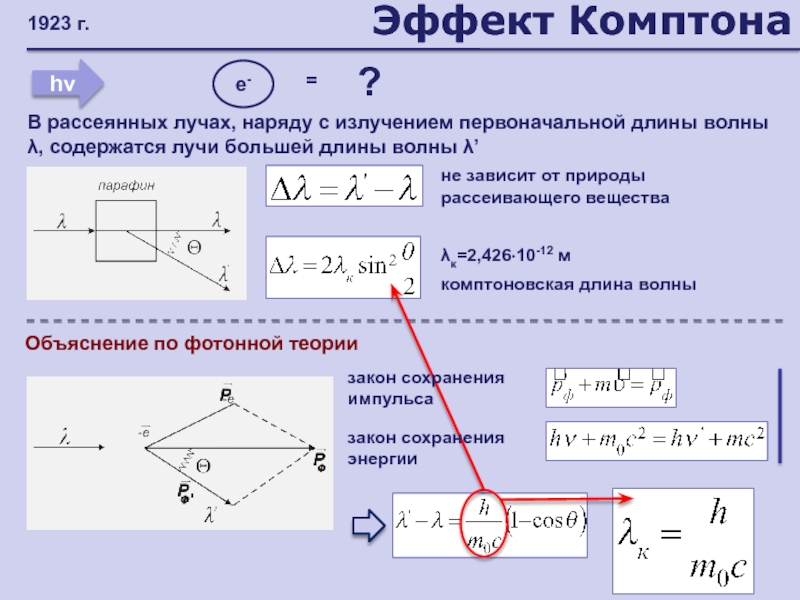
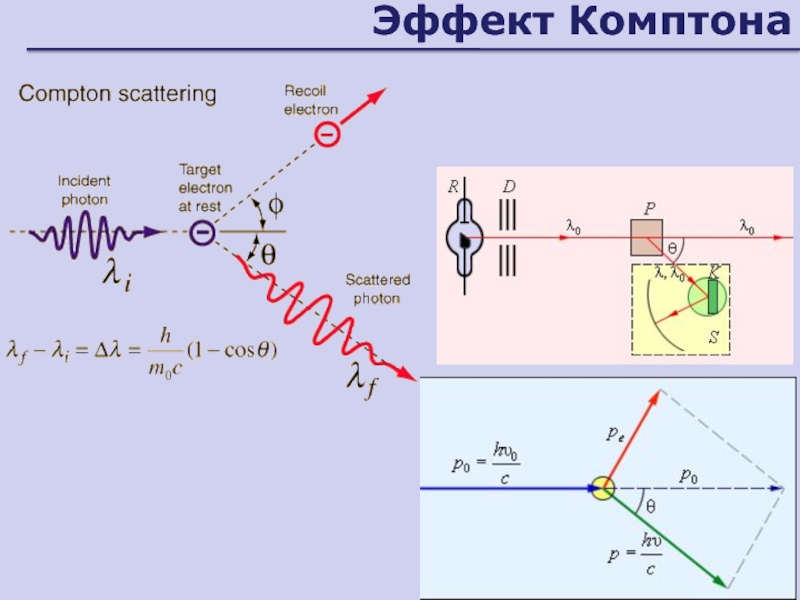



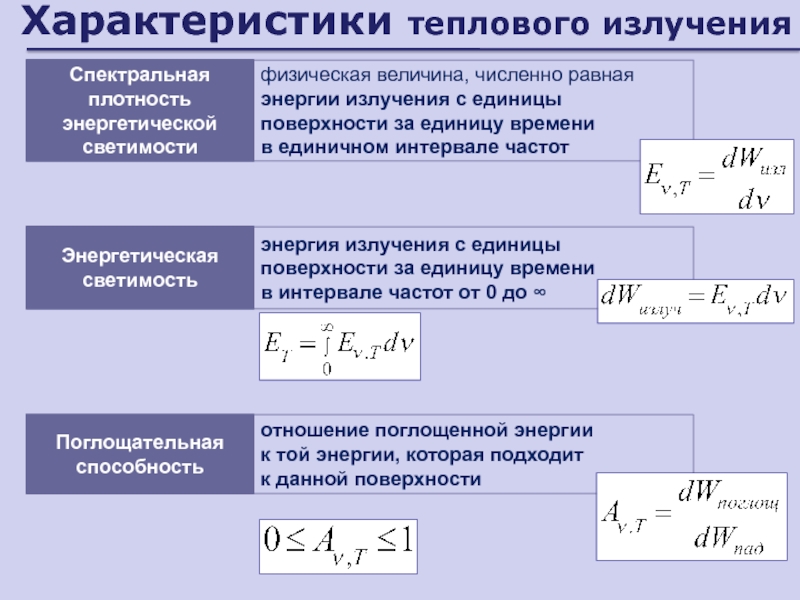
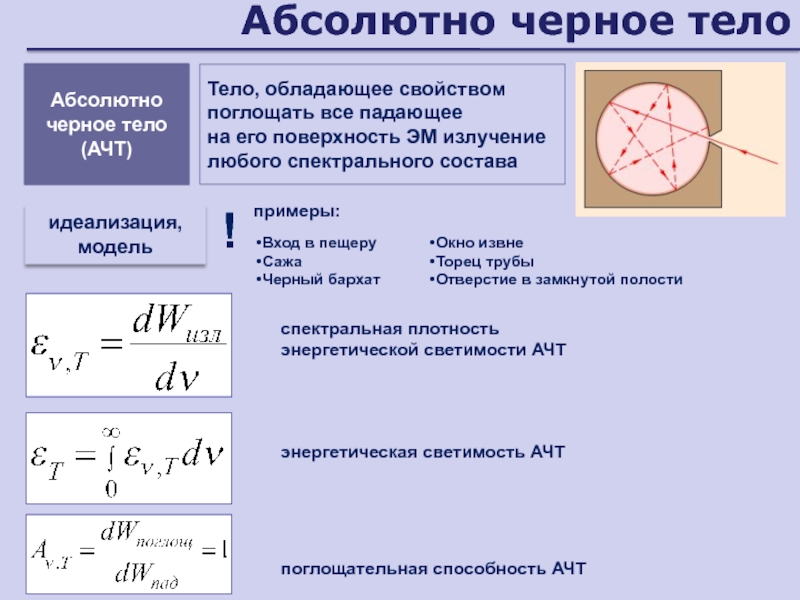
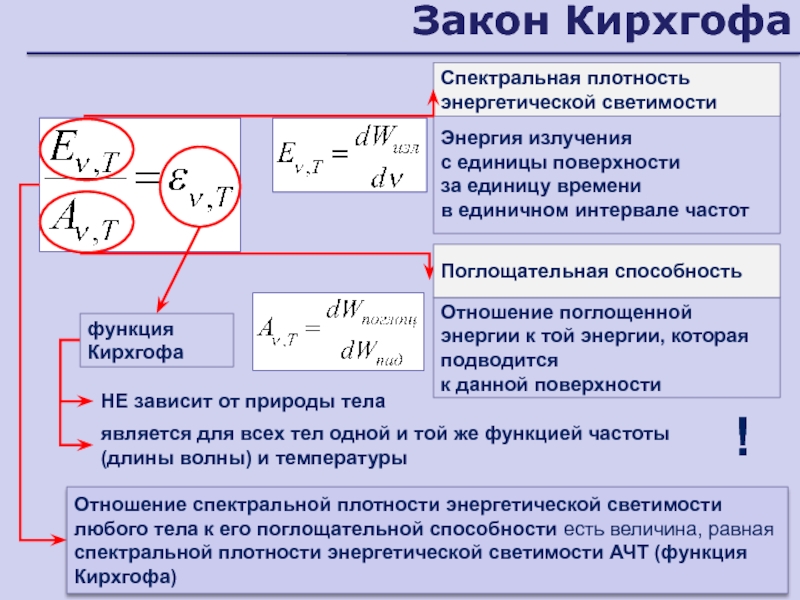


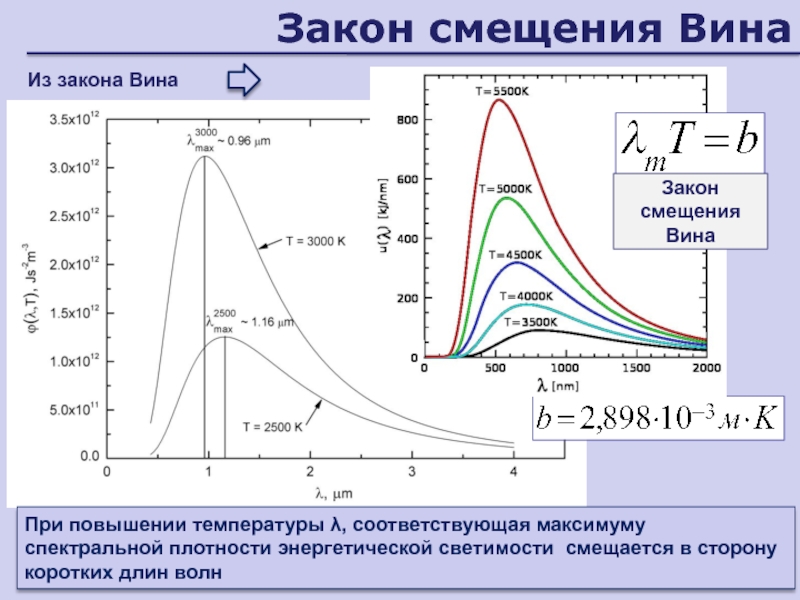
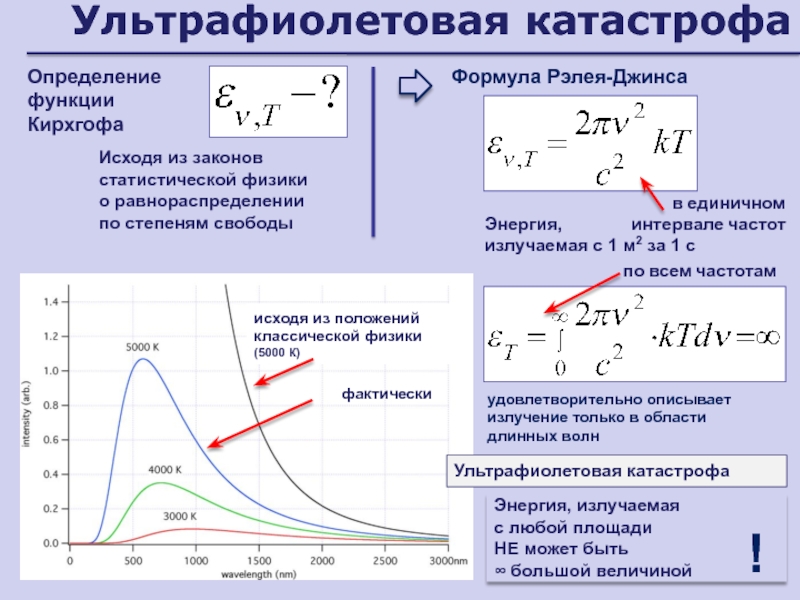
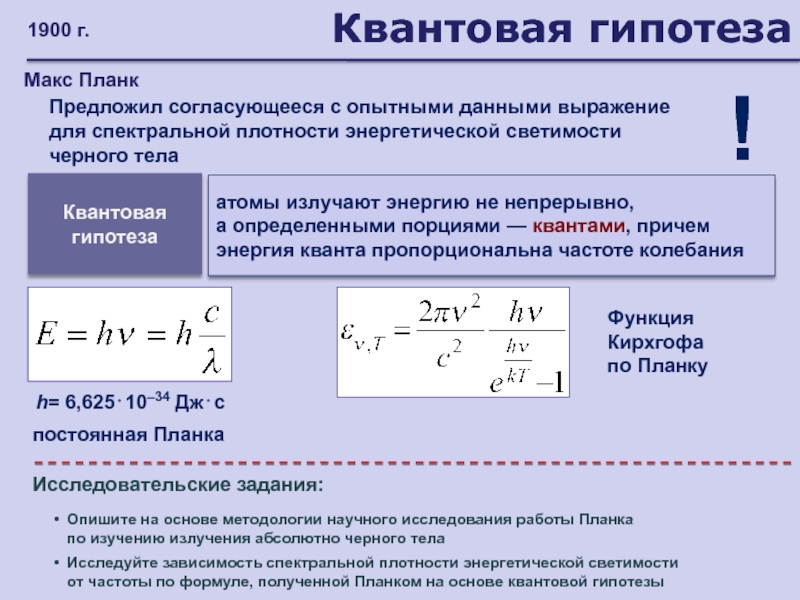
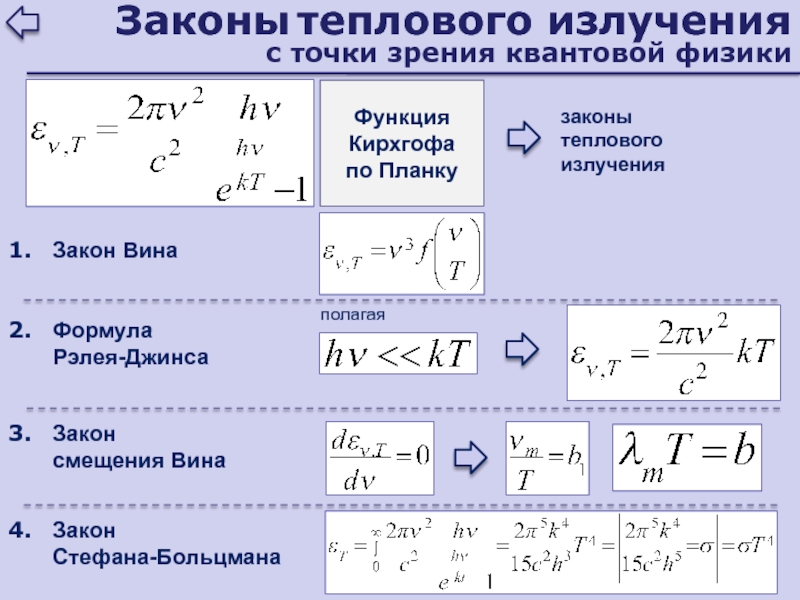





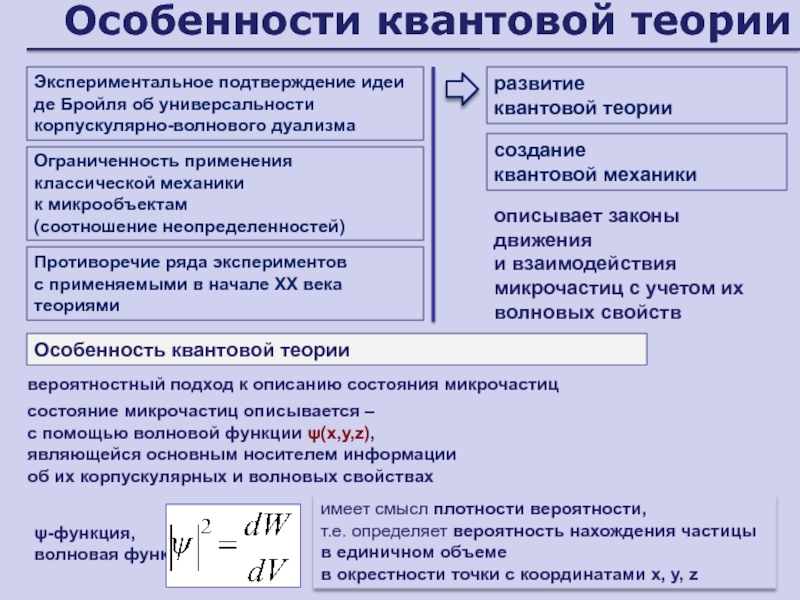





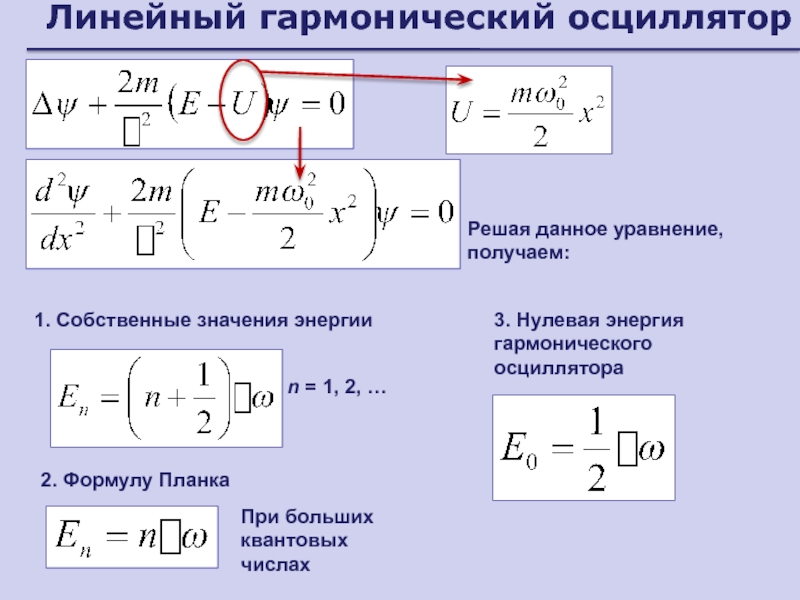

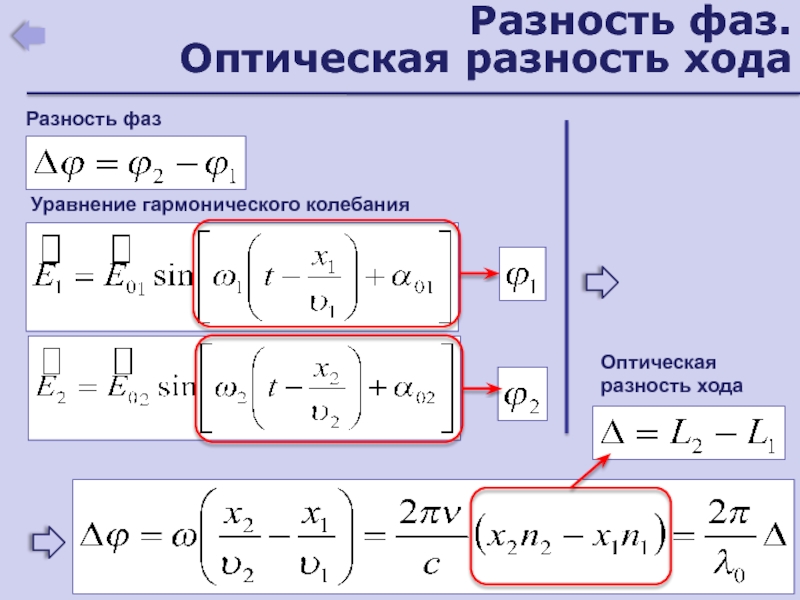
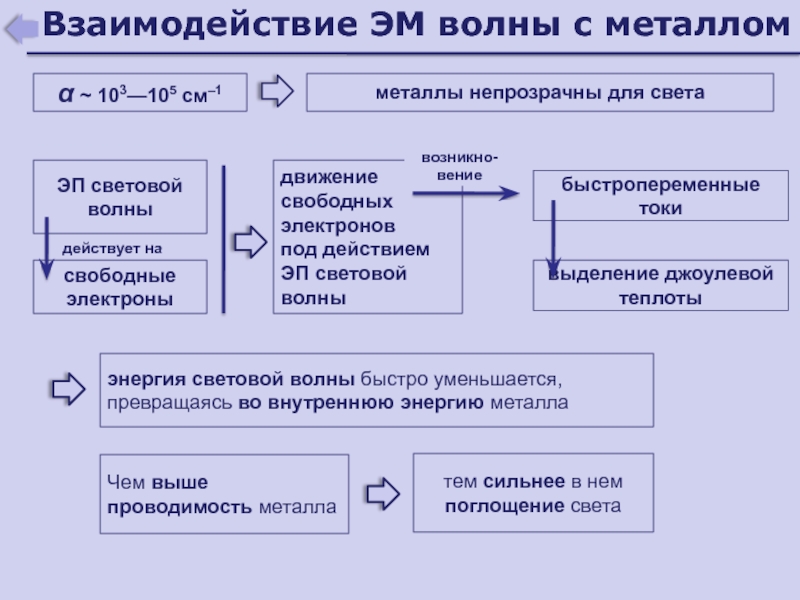


![Оптика и квантовая физика Макс ПланкМакс Карл Эрнст Людвиг Планк[1] (нем. Max Karl Ernst Ludwig Planck; 23 апреля 1858, Киль — 4 Макс ПланкМакс Карл Эрнст Людвиг Планк[1] (нем. Max Karl Ernst Ludwig Planck; 23 апреля 1858, Киль — 4 октября 1947, Гёттинген) — выдающийся немецкий физик. Как основатель квантовой](/img/thumbs/79aea4ca182683bf3815d1b262839744-800x.jpg)