Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Оптимизация контуров регулирования
Содержание
- 1. Оптимизация контуров регулирования
- 2. Оптимизация контуров регулирования
- 3. Оптимизация контуров регулированияПередаточные функции замкнутых систем АЭП1.
- 4. Оптимизация контуров регулированияОптимизация на модульный оптимум.1. Объект
- 5. Оптимизация на модульный оптимумПередаточная функция замкнутого контура:
- 6. Оптимизация на модульный оптимумОсциллограммы выходного сигнала при
- 7. Оптимизация на модульный оптимумЛАЧХ контура, оптимизированного на МО.
- 8. Оптимизация на модульный оптимумЗамкнутый контур, оптимизированный на МООптимизация на МО с использованием ЛАЧХ
- 9. Оптимизация на модульный оптимумОсциллограммы сигналов при различных настройках
- 10. Оптимизация на модульный оптимумОшибка регулирования при настройке
- 11. Оптимизация на модульный оптимум2. Оптимизация контура на
- 12. Оптимизация на модульный оптимумВарианты реализации контура регулирования
- 13. Оптимизация контура на симметричный оптимум Построение астатической
- 14. Оптимизация контура на симметричный оптимум Подстановка полученных
- 15. Оптимизация контура на симметричный оптимум Повышенное перерегулирование
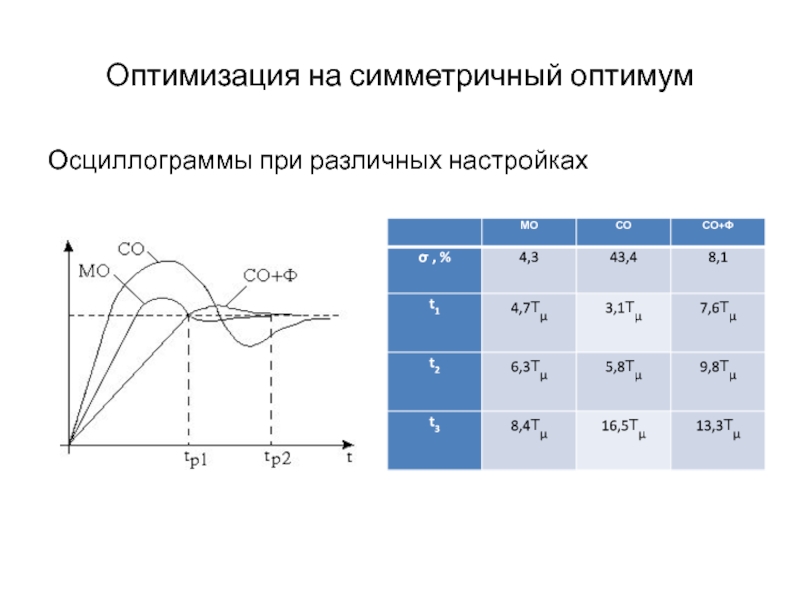
- 16. Оптимизация на симметричный оптимумОсциллограммы при различных настройках
- 17. Скачать презентанцию
Оптимизация контуров регулирования
Слайды и текст этой презентации
Слайд 1Оптимизация контуров регулирования
Цель оптимизации- поиск регулятора при котором выходной сигнал
Слайд 2Оптимизация контуров регулирования
При единичной обратной связи
При наличии датчика обратной связи
Идеальный режим
Решение идеальной задачи ступает в противоречие с техническими возможностями и экономической целесообразностью. На практике инерционность объекта компенсируют насколько это возможно и насколько это целесообразно. В контуре оставляют малую инерционность для сохранения помехоустойчивости контура.
Слайд 3Оптимизация контуров регулирования
Передаточные функции замкнутых систем АЭП
1.
при 2а0а2 = а12
2.
при 2а0а2 = а12 2а1а3 = а22
Слайд 4Оптимизация контуров регулирования
Оптимизация на модульный оптимум.
1. Объект контура содержит большую
(То) и малую (Тµ) инерционности:
Для компенсации большой инерционности и для
придания контуру астатических свойств нужен ПИ регулятор, ,у которого: Тиз= То, а Кр=?
Найдем
Слайд 5Оптимизация на модульный оптимум
Передаточная функция замкнутого контура:
где
Из условия оптимизации на модульный оптимум: ,
запишем Откуда находим:
После подстановки имеем:
k0kp = b0 = a0; T0 = a1; T0T = a2.
.
2a0a2 = a12
2kpk0T0T = T02;
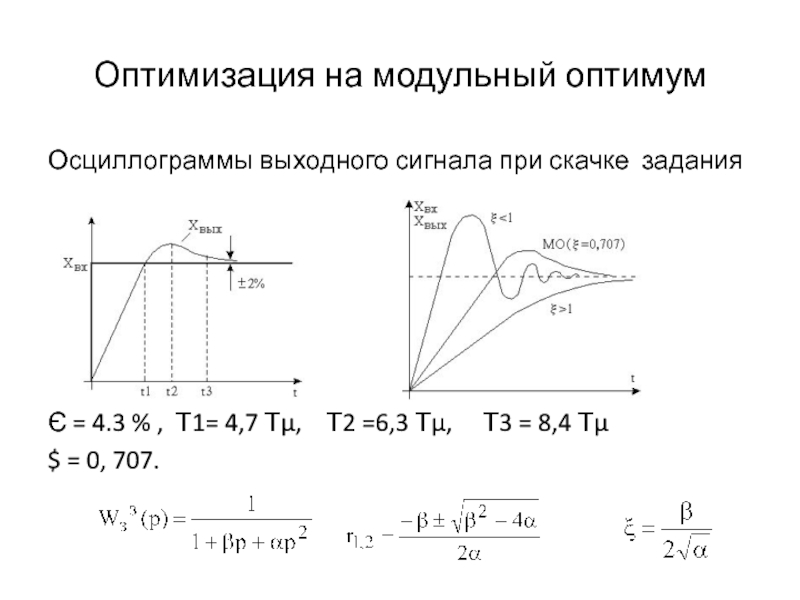
Слайд 6Оптимизация на модульный оптимум
Осциллограммы выходного сигнала при скачке задания
Є =
4.3 % , Т1= 4,7 Тµ, Т2 =6,3 Тµ,
Т3 = 8,4 Тµ$ = 0, 707.
Слайд 8Оптимизация на модульный оптимум
Замкнутый контур, оптимизированный на МО
Оптимизация на МО
с использованием ЛАЧХ
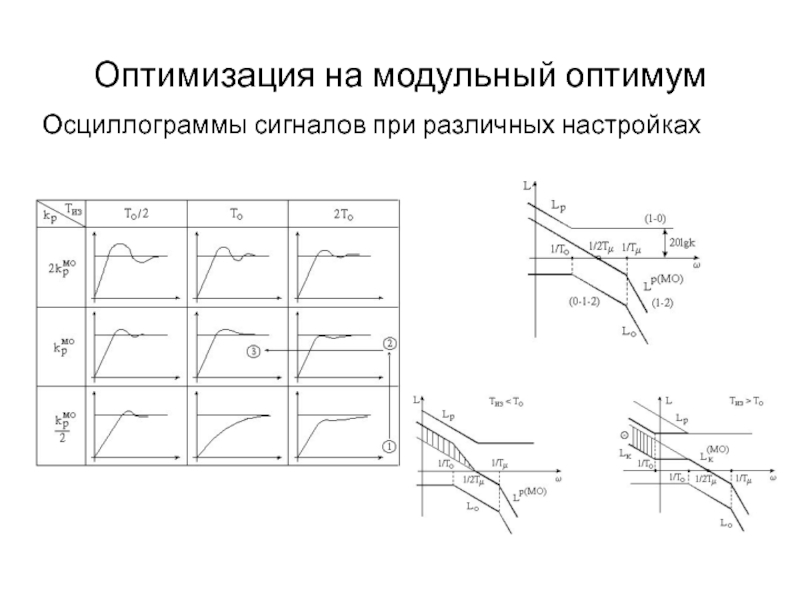
Слайд 10Оптимизация на модульный оптимум
Ошибка регулирования при настройке на МО
Х(р) = Wош (р)Хвх (р).
Слайд 11Оптимизация на модульный оптимум
2. Оптимизация контура на МО в объекте
которого интегрирующее звено и звено с малой постоянной времени
Получили регулятор
П типа, при котором контур в общем случае -статический.По заданию контур –астатический (т.к. есть интегрирующее звено в объекте).
По возмущению –м.б. как статическим, так и астатическим.
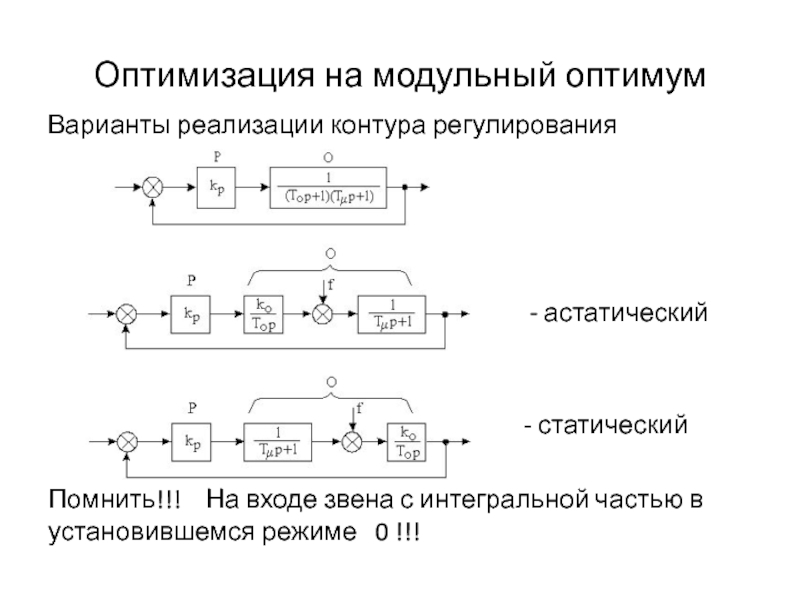
Слайд 12Оптимизация на модульный оптимум
Варианты реализации контура регулирования
- астатический
- статический
Помнить!!! На входе звена с интегральной частью в установившемся режиме 0 !!!
Слайд 13Оптимизация контура на симметричный оптимум
Построение астатической контура в объекте
которого интегрирующее звено и звено с малой постоянной времени.
Надо применить
ПИ –регулятор:2а0а2 = а12 2kpk0ТизТ0 = kp2k02Тиз2 2Т0 = kpk0Тиз;
2а1а3 = а22 2kpk0Тиз2Т0Т = Тиз2Т02 2kpk0T = T0;
Тиз = 4Т;
Слайд 14Оптимизация контура на симметричный оптимум
Подстановка полученных Кр и Тиз
позволяют получить:
Т1=3,1 Тµ, Т2 = 5,8 Тµ, Т3 = 16,5Тµ Название настройки – по виду ЛАЧХ
(частота среза симметрична частотам сопряжения)
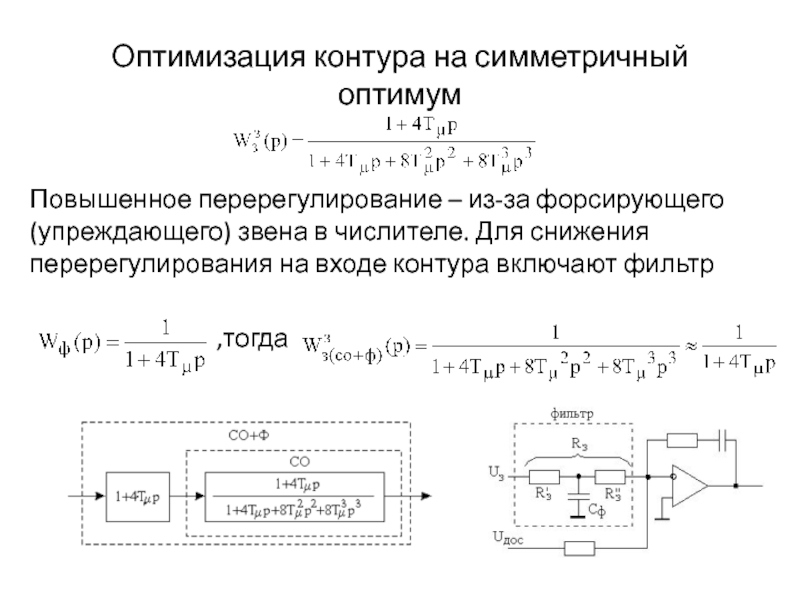
Слайд 15Оптимизация контура на симметричный оптимум
Повышенное перерегулирование – из-за форсирующего
(упреждающего) звена в числителе. Для снижения перерегулирования на входе контура
включают фильтр,тогда