Основные понятия метрологии Точность измерений — одна из характеристик качества

отражающая близость к нулю погрешности результата измерения. Это означает, что

высокая точность измерений соответствует малым погрешностям, и наоборот. Количественно точность может быть выражена обратной величиной модуля относительной погрешности.

Воспроизводимостью (результатов) измерений считается близость результатов измерений одной и той же величины, полученных в разных местах, разными методами, разными средствами, разными операторами, в разное время, но приведенных к одним и тем же условиям измерений.

Сходимостью (результатов) измерений считается близость друг к другу результатов измерений одной и той же величины, выполненных повторно одними и теми же средствами, одним и тем же методом в одинаковых условиях и с одинаковой тщательностью.

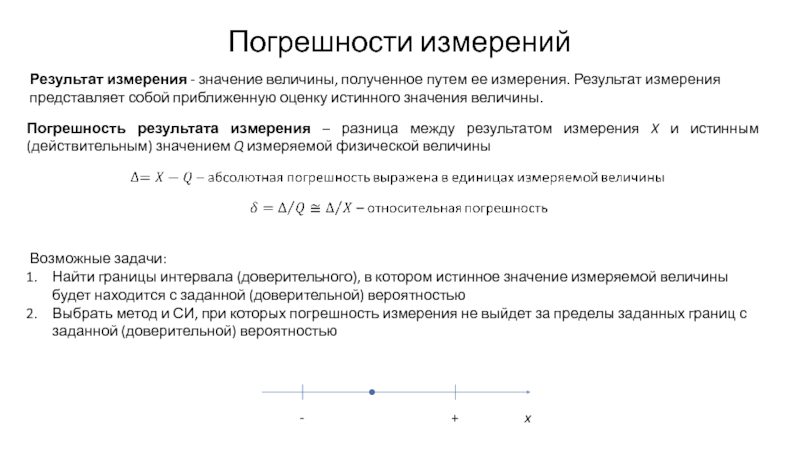
Погрешность СИ – разность между показанием СИ и истинным (действительным) значением измеряемой физической величины.

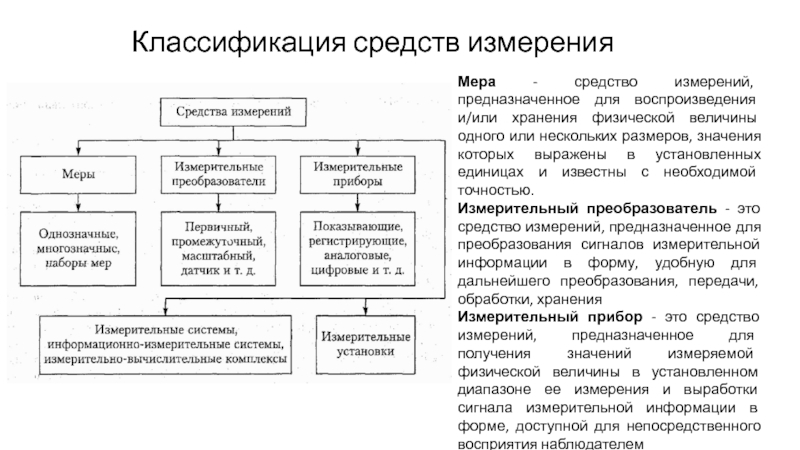
Средством измерений (СИ) именуется техническое средство, предназначенное для измерений, имеющее нормированные метрологические характеристики, воспроизводящее и (или) хранящее единицу физической величины, размер которой принимают неизменным (в пределах установленной погрешности) в течение известного интервала времени.

их результаты выражаются в узаконенных единицах, размеры которых в установленных

пределах равны размерам единиц, воспроизводимых первичными эталонами, а погрешности результатов измерении известны и с заданной вероятностью не выходят за установленные пределы.

Диапазон измерений СИ – область возможных значений измеряемой величины для данного СИ.

Градуировка средства измерений представляет собой определение зависимости между значениями величин на выходе и входе СИ, составленной в виде таблицы, графика или формулы.

Поверкой средств измерений называется установление органом государственной метрологической службы (или другим официально уполномоченным органом, организацией) пригодности СИ к применению на основании экспериментально определяемых метрологических характеристик и подтверждения их соответствия установленным обязательным требованиям.

Калибровка СИ — это совокупность операций, устанавливающих соотношение между значением величины, полученным с помощью данного СИ, и соответствующим значением величины, полученным с помощью эталона, с целью определения действительных метрологических характеристик этого СИ.

хранения физической величины одного или нескольких размеров, значения которых выражены

в установленных единицах и известны с необходимой точностью.
Измерительный преобразователь - это средство измерений, предназначенное для преобразования сигналов измерительной информации в форму, удобную для дальнейшего преобразования, передачи, обработки, хранения
Измерительный прибор - это средство измерений, предназначенное для получения значений измеряемой физической величины в установленном диапазоне ее измерения и выработки сигнала измерительной информации в форме, доступной для непосредственного восприятия наблюдателем

и истинным (действительным) значением Q измеряемой физической величины
Результат измерения -

значение величины, полученное путем ее измерения. Результат измерения представляет собой приближенную оценку истинного значения величины.

Возможные задачи:
Найти границы интервала (доверительного), в котором истинное значение измеряемой величины будет находится с заданной (доверительной) вероятностью
Выбрать метод и СИ, при которых погрешность измерения не выйдет за пределы заданных границ с заданной (доверительной) вероятностью

при исправных средствах измерений и корректных действиях экспериментатора (оператора) не

должны появляться

Систематическая погрешность – составляющая погрешности результата измерения, остающаяся постоянной для данного ряда измерений или же закономерно изменяющаяся при повторных измерениях физической величины постоянного размера

упрощениями, положенными в основу методики
Инструментальные (приборные) погрешности — погрешности, которые определяются

погрешностями применяемых СИ и вызываются несовершенством принципа действия, неточностью градуировки шкалы, изменением свойств СИ в процессе хранения и эксплуатации и т. п.

Погрешности, связанные с неправильной установкой элементов измерительных схем, например, неточной юстировкой

эталон справа

различным воздействиям, которые влияют на результаты измерений:
посторонняя засветка;
внешнее электромагнитное поле;
влажность;
изменение

температуры СИ за счет температуры воздуха и источников теплового излучения (борьба – термостабилизация, термокомпенсация);
радиация, вибрации и т. п.

образом (по знаку и значению) в серии повторных измерений физической

величины постоянного размера, проведенных с одинаковой тщательностью в одинаковых условиях

Некоторые возможные причины, вызывающие случайные погрешности:
нестабильность выходных токов или напряжений стабилизированных источников питания, к которым подключены источники и приемники излучения;
случайные погрешности СИ электрических величин;
погрешности округления показаний СИ;
конвекционные потоки вблизи нагретых источников излучения;
флуктуации сигнала приемников излучения (темновой ток);
погрешности вносимые органом зрения (в визуальной фотометрии).

значения, которые можно заранее перечислить‚ называются прерывными, или дискретными случайными

величинами.

Пример. При помощи цифрового люксметра с дискретностью отсчета 1 лк получены десять значений: 26, 24, 26, 28, 23, 24, 25, 24, 26, 25 лк

Среднее арифметическое значение

всякое соотношение, устанавливающее связь между возможными значениями случайной величины и

соответствующими им вероятностями.

Распределение дискретной случайной величины

друга и непрерывно заполняют некоторый промежуток, называются непрерывными случайными величинами.

Функция распределения случайной величины,
или интегральная функция распределения случайной величины,
или интегральный закон распределения случайной величины

Некоторые свойства функций распределения вероятности

Плотность вероятности,
или дифференциальная функция распределения вероятностей,
или дифференциальный закон распределения вероятностей

отсчетов случайные отклонения от среднего значения, равные по величине, но

различные по знаку, встречаются одинаково часто.
Аксиома монотонного убывания плотности вероятностей: чаще всего встречаются меньшие отклонения‚ a большие отклонения встречаются тем реже, чем они больше.

не превышает с фиксированной вероятностью
p(x)

надежным с вероятностью 1-, если попадает в интервал между квантилями

(1, 2) – в доверительный интервал с соответствующей доверительной вероятностью

Примеры значений t доверительной вероятности Pд для нормального распределения