Основные свойства электрических цепей: принцип эквивалентности, преобразование схем.

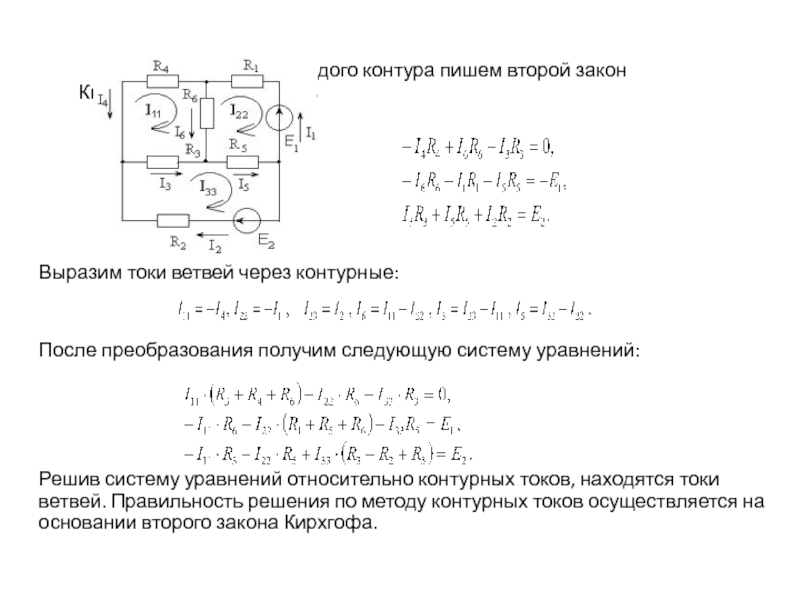
сложных электрических цепей постоянного тока: применение законов Кирхгофа, метод контурных

токов. Уравнение баланса электрической мощности.

В основе методов преобразования электрических схем лежит принцип эквивалентности, согласно которому токи и напряжения в ветвях схемы не затронутых преобразованием остаются неизменными.
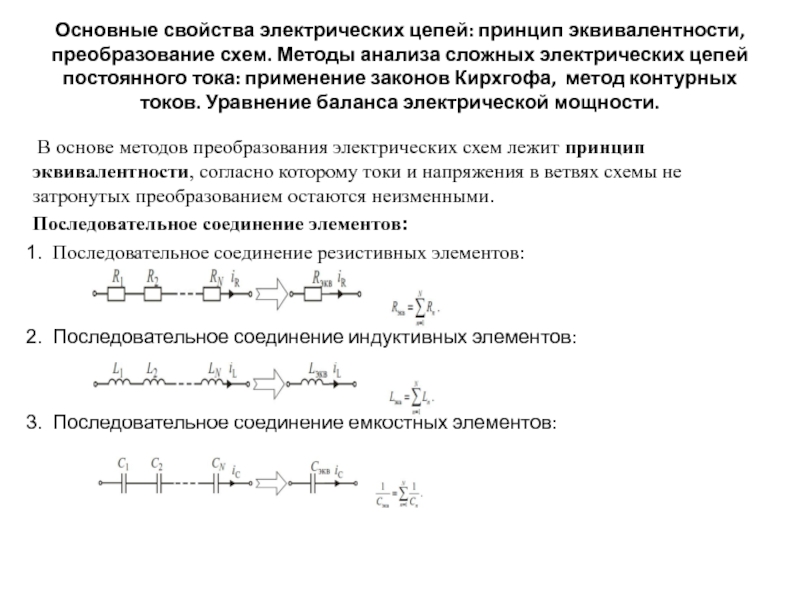
Последовательное соединение элементов:
Последовательное соединение резистивных элементов:


Последовательное соединение индуктивных элементов:


Последовательное соединение ёмкостных элементов:

Параллельное соединение ёмкостных элементов:



4. Смешанное соединение резистивных элементов:

«звезды» в «треугольник»



Для проводимостей из «звезды» в «треугольник»



Для

сопротивлений из «треугольника» в «звезду»



Для проводимостей из «треугольника» в «звезду»

метод контурных токов. Уравнение баланса электрической мощности.
Анализ электрических цепей с

одним источником энергии проводится двумя методами: методом эквивалентного преобразования (свертывания схемы) и методом пропорциональных величин.
При методе свертывания схемы определяется входное или эквивалентное сопротивление путем преобразования сопротивлений: параллельного соединения в последовательное и обратно, треугольника в звезду и обратно и т.д., что упрощает отдельные участки схемы и приводит к одному эквивалентному (входному) сопротивлению относительно зажимов источников питания. В результате схема упрощается и расчет такой схемы можно произвести , используя закон Ома.
К методом анализа сложных цепей относятся:
Метод, основанный на применении законов Кирхгофа.
Метод контурных токов.
Метод узловых потенциалов.
Метод наложения.
Метод эквивалентного генератора.
Классическим методом расчета электрических цепей с несколькими источниками является непосредственное применение законов Кирхгофа.

положительное направление токов во всех ветвях схемы;
2. Выбрать положительное направление

обхода контура;
3. Составить уравнения по законам Кирхгофа;
по первому закону Кирхгофа составить nу-1 уравнение, по второму закону Кирхгофа составить nв –nу +1. Общее число уравнений равно числу ветвей в схеме;
4. Полученную систему уравнений решают относительно неизвестных токов.
Составим систему уравнений для нахождения токов ветвей для схемы, изображенной на рисунке: Данная схема имеет четыре узла и шесть ветвей. Система уравнений по законам Кирхгофа имеет следующий вид:

I1, I2, I5 через I4, I6,I3, получим:









Решая данную систему уравнений,

можно найти токи ветвей.
Число совместно решаемых уравнений равно числу ветвей схемы (числу неизвестных токов ветвей), поэтому его применение не всегда целесообразно.
В качестве переменных в методе контурных токов принимаются контурные токи.
В схеме выделяют независимые контуры. В каждом контуре произвольно выбирают направление контурных токов. За контурные токи удобно принять токи внешних ветвей схемы, которые входят только в данный контур.
Уравнения составляются на основе второго закона Кирхгофа, выражая токи ветвей через контурные токи.

через контурные:


После преобразования получим следующую систему уравнений:




Решив систему уравнений относительно

контурных токов, находятся токи ветвей. Правильность решения по методу контурных токов осуществляется на основании второго закона Кирхгофа.

алгебраической сумме мощностей, потребляемых потребителями.


Где -

алгебраическая сумма мощностей, генерируемая источниками э.д.с.;

- алгебраическая сумма мощностей, генерируемая источниками тока;

- суммарная мощность, потребляемая потребителями в цепи.


Эти суммы алгебраические. Источник может как вырабатывать, так и потреблять электрическую энергию (заряд аккумулятора).

Уравнение баланса электрической мощности.

источника записывают в уравнении баланса мощностей с положительным знаком. Он

работает в режиме генератора. При противоположных направлениях ЭДС и тока мощность в уравнении баланса учитывают с отрицательным знаком (режим потребителя).
Определение знака мощности источника тока поясняет, на котором показана разметка зажимов источника тока, вырабатывающего (а) или потребляющего (б) электрическую энергию. Ток и напряжение U направлены в сторону уменьшения потенциала, что и позволяет разметить зажимы источника.






Мощность потребителей (нагрузок)
Эта сумма арифметическая.
Погрешность расчета не должна превышать (1–3) %.