Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Основы математической логики
Содержание
- 1. Основы математической логики
- 2. ЛогикаНаука, изучающая методы установления истинности или ложности одних высказываний на основе истинности или ложности других высказываний
- 3. ВысказываниеСуждение, в котором что-либо утверждается или отрицается. Может быть истинным и ложным
- 4. Логические величиныИСТИНА, TRUE, 1ЛОЖЬ, FALSE, 0
- 5. Логическая переменнаяВысказывание, которое может быть истинно или ложно
- 6. Логическое выражениеСложное высказывание, состоящее из нескольких высказываний и связок в виде логических операций
- 7. Логические операции: НЕИнверсия или ОтрицаниеОбозначается символом ¬
- 8. Логические операции: ИЛИДизъюнкцияОбозначается символом v
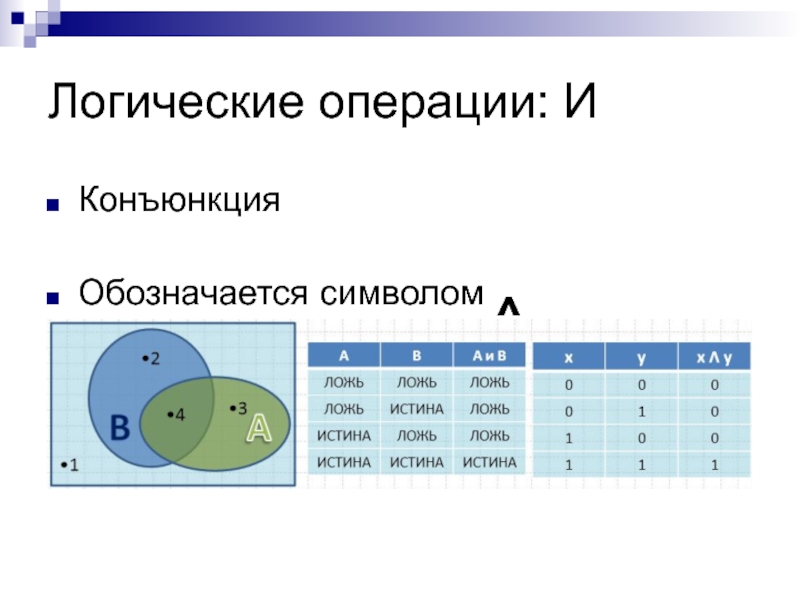
- 9. Логические операции: ИКонъюнкцияОбозначается символом ^
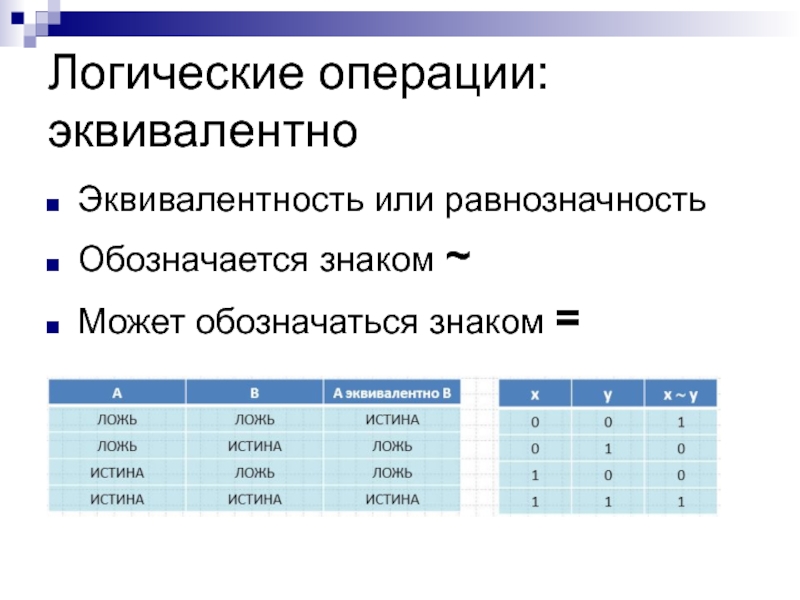
- 10. Логические операции: эквивалентноЭквивалентность или равнозначностьОбозначается знаком ~Может обозначаться знаком =
- 11. Приоритет операцийОтрицаниеКонъюнкцияДизъюнкцияЭквивалентность
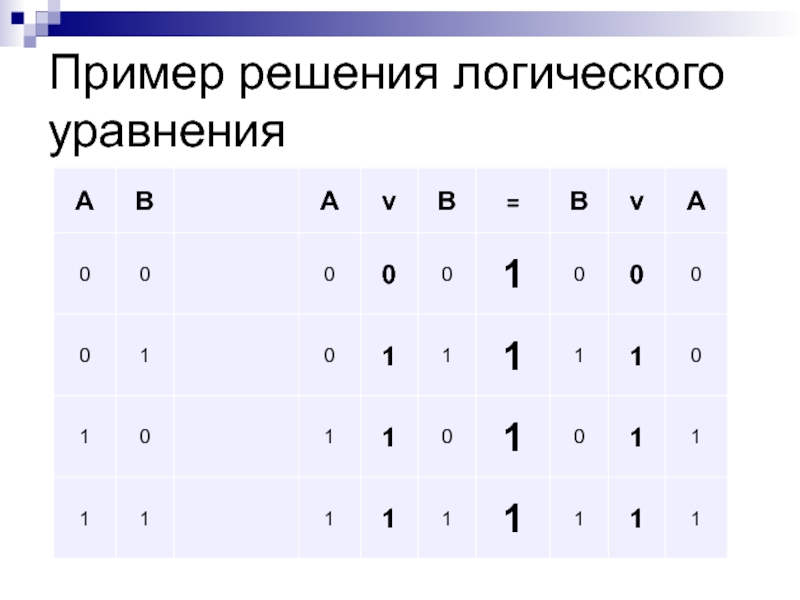
- 12. Пример решения логического уравнения
- 13. ЗадачаДоказать закон двойного отрицания¬ (¬ А) =
- 14. Скачать презентанцию
ЛогикаНаука, изучающая методы установления истинности или ложности одних высказываний на основе истинности или ложности других высказываний
Слайды и текст этой презентации
Слайд 2Логика
Наука, изучающая методы установления истинности или ложности одних высказываний на
основе истинности или ложности других высказываний
Слайд 3Высказывание
Суждение, в котором что-либо утверждается или отрицается. Может быть истинным
и ложным
Слайд 6Логическое выражение
Сложное высказывание, состоящее из нескольких высказываний и связок в
виде логических операций
Слайд 10Логические операции: эквивалентно
Эквивалентность или равнозначность
Обозначается знаком ~
Может обозначаться знаком =
Слайд 13Задача
Доказать закон двойного отрицания
¬ (¬ А) = А
Доказать закон де
Моргана
¬ (А ^ В) = ¬А v ¬В
¬ (А v
В) = ¬А ^ ¬В
