Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Основы теории информации
Содержание
- 1. Основы теории информации
- 2. Слайд 2
- 3. Термины - 10Форма мышления, в которой отражаются общие, существенные, отличительные признаки изучаемых объектовПонятие
- 4. Термины - 20Форма мышления, в которой что-либо утверждается или отрицается о предметах и их свойствахСуждение
- 5. Термины - 30Форма мышления, по средствам которой
- 6. Термины - 40Вид дедуктивного умозаключения, построенного из
- 7. Термины - 50Логическая операция, расчленения объема понятия на ряд подмножеств с помощью некоторого признакаДеление
- 8. Термины - 60Вид недедуктивного умозаключения, в котором
- 9. Схемы - 10Как классифицируются понятия по объему?Единичные, общие (конечные и бесконечные) и пустые множества
- 10. Схемы - 20В каких отношениях могут быть сравнимые понятия?
- 11. Схемы - 20Сравнимые понятия:1) Совместимыеравнозначныеперекрещивающиесяподчиняющие 2) Несовместимыесоподчиненныепротивоположныепротиворечащие
- 12. Схемы - 30Классификация суждений по форме
- 13. Схемы - 30Простые сужденияУтвердительныеОтрицательныеОбщеутвердительныеЧастноутвердительныеОбщеотрицательныеЧастноотрицательные
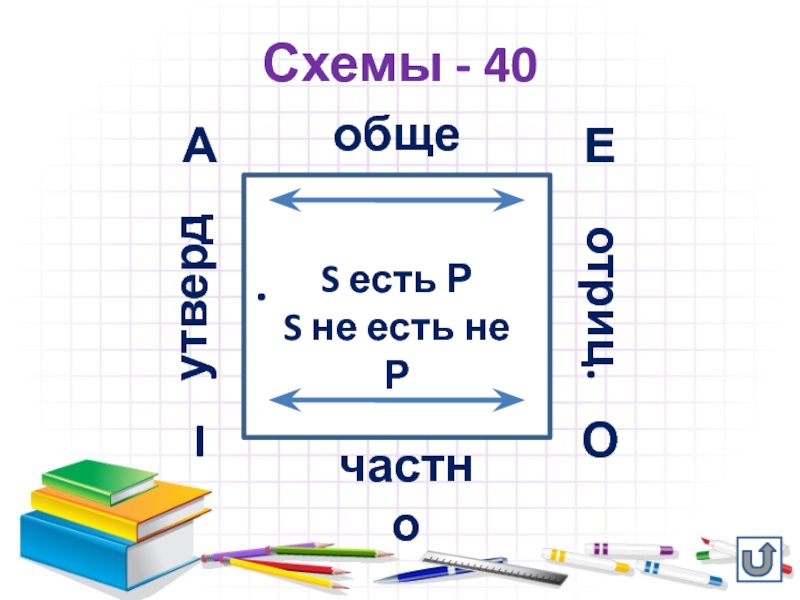
- 14. Схемы - 40Представить логический квадрат для превращения
- 15. Схемы - 40АЕIОобщечастноутверд.отриц.S есть РS не есть не Р
- 16. Схемы - 50Виды непосредственных умозаключенийПревращение, обращение, противопоставление предикату, умозаключение по логическому квадрату
- 17. Схемы - 60Как будет выглядеть фигура следующего силлогизма:Все ягоды – плоды.Клубника – ягода.Клубника – плод.
- 18. Схемы - 60ММSР
- 19. Секрет - 10Назовите виды сложных сужденийКонъюнкция, дизъюнкция, импликация, эквиваленция, инверсия
- 20. Секрет - 20Равносильны ли формулы между собой?Формулы равносильны
- 21. Секрет - 30Постройте умозаключение по логическому квадрату к следующему высказыванию «Некоторые студенты не являются школьниками»Не существует
- 22. Секрет - 40Отрицанием высказывания «Все школьники предпочитают
- 23. Секрет - 50Постройте логическую формулу (выражение) для
- 24. Секрет - 60Постройте обращение для следующего суждения «Все квадраты – равносторонние прямоугольники»Все равносторонние прямоугольники - квадраты
- 25. Скачать презентанцию
Термины - 10Форма мышления, в которой отражаются общие, существенные, отличительные признаки изучаемых объектовПонятие
Слайды и текст этой презентации
Слайд 3Термины - 10
Форма мышления, в которой отражаются общие, существенные, отличительные
признаки изучаемых объектов
Слайд 4Термины - 20
Форма мышления, в которой что-либо утверждается или отрицается
о предметах и их свойствах
Суждение
Слайд 5Термины - 30
Форма мышления, по средствам которой из одного или
нескольких суждений, называемых посылками, мы получаем заключение
Умозаключение
Слайд 6Термины - 40
Вид дедуктивного умозаключения, построенного из двух категорических суждений,
в котором S и P связаны средним термином
Категорический силлогизм
Слайд 7Термины - 50
Логическая операция, расчленения объема понятия на ряд подмножеств
с помощью некоторого признака
Деление
Слайд 8Термины - 60
Вид недедуктивного умозаключения, в котором суждение о присутствии
признака некоторого объекта выводится на основании его сходства с другим
объектомАналогия
Слайд 9Схемы - 10
Как классифицируются понятия по объему?
Единичные, общие (конечные и
бесконечные) и пустые множества
Слайд 11Схемы - 20
Сравнимые понятия:
1) Совместимые
равнозначные
перекрещивающиеся
подчиняющие
2) Несовместимые
соподчиненные
противоположные
противоречащие
Слайд 13Схемы - 30
Простые суждения
Утвердительные
Отрицательные
Общеутвердительные
Частноутвердительные
Общеотрицательные
Частноотрицательные
Слайд 16Схемы - 50
Виды непосредственных умозаключений
Превращение, обращение, противопоставление предикату, умозаключение по
логическому квадрату
Слайд 17Схемы - 60
Как будет выглядеть фигура следующего силлогизма:
Все ягоды –
плоды.
Клубника – ягода.
Клубника – плод.
Слайд 19Секрет - 10
Назовите виды сложных суждений
Конъюнкция, дизъюнкция, импликация, эквиваленция, инверсия
Слайд 21Секрет - 30
Постройте умозаключение по логическому квадрату к следующему высказыванию
«Некоторые студенты не являются школьниками»
Не существует
Слайд 22Секрет - 40
Отрицанием высказывания «Все школьники предпочитают изучать информатику» является:
А)
Некоторые школьники не предпочитают изучать информатику.
Б) Некоторые школьники предпочитают изучать
не информатику.В) Неверно, что некоторые школьники предпочитают изучать информатику.
Г) Все школьники предпочитают не изучать информатику.
А
Слайд 23Секрет - 50
Постройте логическую формулу (выражение) для следующего высказывания «Я
поеду в Москву, и если встречу там друзей, то мы
интересно проведем время».
Слайд 24Секрет - 60
Постройте обращение для следующего суждения «Все квадраты –
равносторонние прямоугольники»
Все равносторонние прямоугольники - квадраты
