Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Отношения и отображения
Содержание
- 1. Отношения и отображения
- 2. ОтношенияОпределение. Пусть X и Y - два произвольных множества. Если какому-либо
- 3. Не исключено, что X=Y, тогда говорят, что отношение
- 4. xRy, x∈X, y∈Y - x и y находятся в отношении R.xRy, x∈X, y∈Y - x и y не находятся в отношении R.
- 5. Рассмотрим отношение R между множествами X и Y. Графиком отношения R называется множество Γ={(x,y)|x∈X, y∈Y,
- 6. Слайд 6
- 7. Слайд 7
- 8. Всякое отношение имеет график - некоторое подмножество
- 9. Отношение эквивалентностиОпределение. Отношение R, заданное на множестве X, называется отношением
- 10. Слайд 10
- 11. С отношением эквивалентности тесно связано разбиение множества
- 12. Слайд 12
- 13. Отношение >Определение. Отношение > заданное на множестве X называется отношением частичного
- 14. Отношение ≥ Определение. Отношение ≥, заданное на множестве X, назывется
- 15. Множество X, в котором определены отношения частичного порядка (строгие и нестрогие) называется частично упорядоченным.
- 16. ОтображенияПусть X и Y - два произвольных множества.Определение. Соответствие, при котором каждому
- 17. Множество X называется областью определения отображения и обозначается X=D(f).E(f) называется множеством значений отображения, и E(f)={y∈Y|∃x∈X, y=f(x)}.Множество Γ(f) называется графиком отображенияΓ(f)={(x,y)∈X×Y, y=f(x),∀x∈X, y∈Y}.
- 18. Пусть f - некоторое отображение из множества X в множество Y. Если x при
- 19. Слайд 19
- 20. Определение. Совокупность всех элементов из множества X, образом которых
- 21. Слайд 21
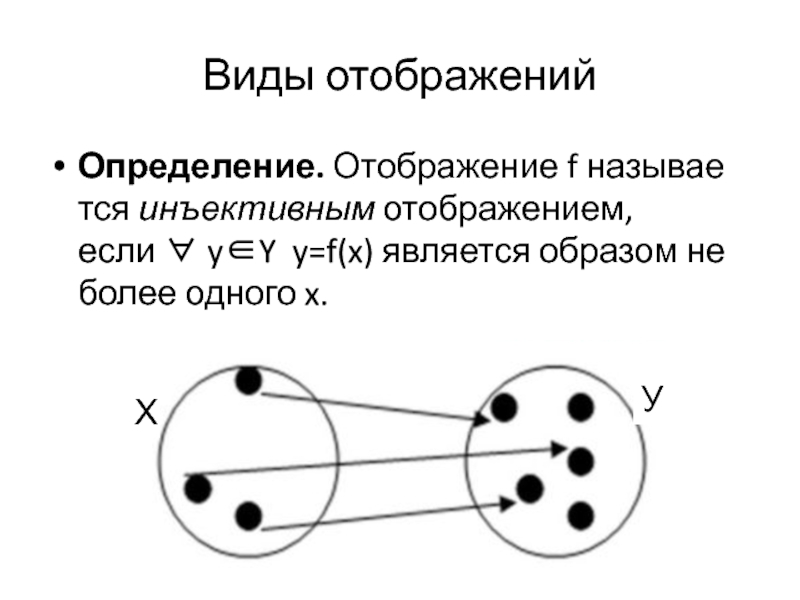
- 22. Виды отображенийОпределение. Отображение f называется инъективным отображением, если ∀ y∈Y y=f(x) является образом не более одного x.ХУ
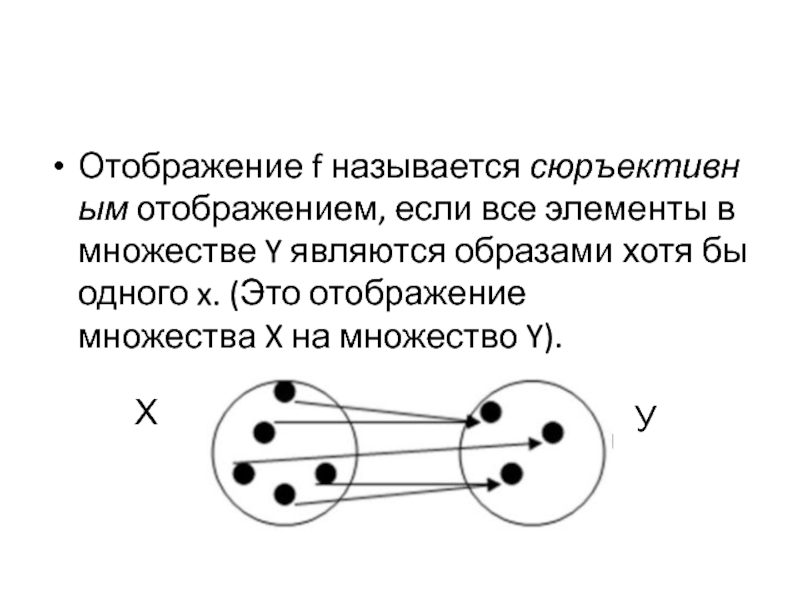
- 23. Отображение f называется сюръективным отображением, если все элементы в множестве Y являются образами хотя бы одного x. (Это отображение множества X на множество Y).ХУ
- 24. Отображение f называется биективным, если оно инъективно и сюръективно, (взаимно однозначным соответствием).ХУ
- 25. ПримерыОтображение. Инъективное, не сюръективное.
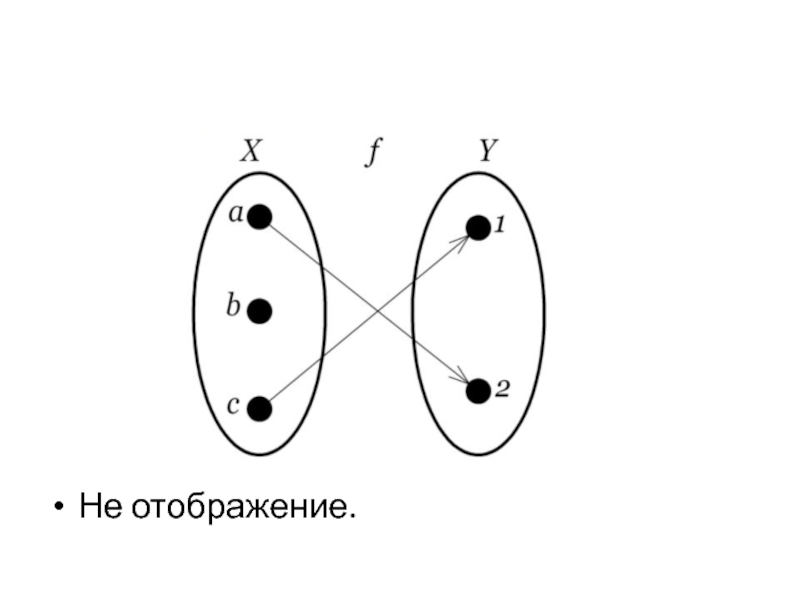
- 26. Не отображение.
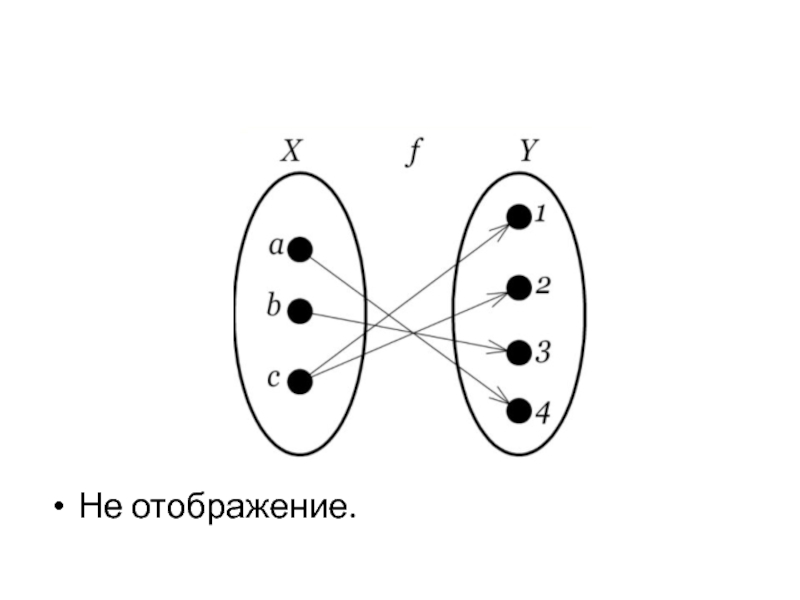
- 27. Не отображение.
- 28. Отображение. Не инъективное, сюръективное.
- 29. Отображение. Инъективное, сюръективное ⇒ биективное.
- 30. Скачать презентанцию
ОтношенияОпределение. Пусть X и Y - два произвольных множества. Если какому-либо элементу x∈X по некоторому правилу сопоставляется элемент y∈Y (один или более), то говорят, что между элементами множеств X и Y установлено отношение (соответствие).
Слайды и текст этой презентации
Слайд 2Отношения
Определение. Пусть X и Y - два произвольных множества.
Если какому-либо элементу x∈X по некоторому
Слайд 3Не исключено, что X=Y, тогда говорят, что отношение установлено между элементами
множества X.
Отношения могут обозначаться символами: R, P, f (специальные элементы ~, =, >, ≤ и
т.д.).
Слайд 4xRy, x∈X, y∈Y - x и y находятся в отношении R.
xRy, x∈X, y∈Y - x и y не находятся в отношении R.
Слайд 5Рассмотрим отношение R между множествами X и Y.
Графиком отношения R называется множество Γ={(x,y)|x∈X, y∈Y, xRy}⊇X×Y.
Определение. Декартовым произведением множеств X и Y называется
множество всевозможных упорядоченных пар, первая компонента которых является элементом множества X,
вторая - множества Y.
Слайд 8Всякое отношение имеет график - некоторое подмножество декартового произведения X и Y, и
наоборот, всякое подмножество R⊂X×Y задаёт некоторое отношение xRy. В связи с этим получаем
следующее определение.Определение. Отношением между элементами множеств X и Y называется подмножество R⊂X×Y.
Слайд 9Отношение эквивалентности
Определение. Отношение R, заданное на множестве X, называется отношением эквивалентности, если оно
обладает следующими свойствами:
1) рефлекивность: xRx ∀x∈X;
2) симметричность: xRy⇒yRx x,y∈X
3)
транзитивность: xRy и yRz⇒xRz ∀ x,y,z∈X.
Слайд 11 С отношением эквивалентности тесно связано разбиение множества на классы.
Определение. Множество X разбито на
классы (подмножества), если выполняются следующие два условия:
объединение всех классов
есть множество X;классы являются попарно не пересекающимися множествами.
Слайд 13Отношение >
Определение. Отношение > заданное на множестве X называется отношением частичного строгого порядка, если
оно обладает следующими свойствами:
1) ассиметричность x>y⇒y>x;
2) транзитивность x>y и y>z⇒x>z
Слайд 14Отношение ≥
Определение. Отношение ≥, заданное на множестве X, назывется отношением частичного нестрогого
порядка, если выполнены следующие условия:
1) x≥x;
2) x≥y и y≥x ⇒
x=y; 3) x≥y и y≥z ⇒ x≥z.
Слайд 15 Множество X, в котором определены отношения частичного порядка (строгие и нестрогие)
называется частично упорядоченным.
Слайд 16Отображения
Пусть X и Y - два произвольных множества.
Определение. Соответствие, при котором каждому из элементов множества X
сопоставляется единственный элемент из множества Y, называется отображением.
Обозначение отображения из множества X в множество Y:
Слайд 17Множество X называется областью определения отображения и обозначается X=D(f).
E(f) называется множеством значений отображения, и E(f)={y∈Y|∃x∈X, y=f(x)}.
Множество Γ(f) называется графиком отображенияΓ(f)={(x,y)∈X×Y, y=f(x),∀x∈X, y∈Y}.
Слайд 18Пусть f - некоторое отображение из множества X в множество Y. Если x при этом отображении сопоставляется y,
то y=f(x).
При этом y называется образом x, или значением отображения f в точке x.
А x -прообразом элемента y.Исходя из определения отображения, видно, что не требуется, чтобы все элементы в множестве Y являлись образами какого-либо x и при том единственного.
Слайд 20Определение. Совокупность всех элементов из множества X, образом которых является y из Y, называется полным прообразом
Y из X.
Обозначается:
Определение. Пусть A⊂X. Совокупность всех элементов f(a), a∈A, называется полным образом множества A при отображении
f.Определение. Пусть B⊂Y. Множество всех элементов из X, образы которых принадлежат множеству B, называется полным прообразом множества B.
Слайд 22Виды отображений
Определение. Отображение f называется инъективным отображением, если ∀ y∈Y y=f(x) является образом не более одного x.
Х
У
Слайд 23Отображение f называется сюръективным отображением, если все элементы в множестве Y являются образами хотя бы одного x.
(Это отображение множества X на множество Y).
Х
У
Слайд 24 Отображение f называется биективным, если оно инъективно и сюръективно, (взаимно однозначным соответствием).
Х
У
