Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Отсечение невидимых частей объектов(Clipping)
Содержание
- 1. Отсечение невидимых частей объектов(Clipping)
- 2. Видовое преобразование
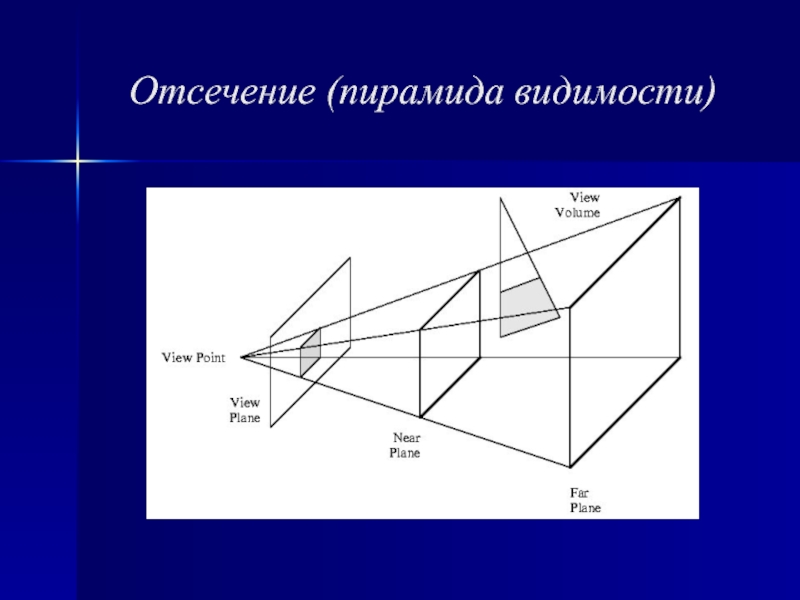
- 3. Отсечение (пирамида видимости)
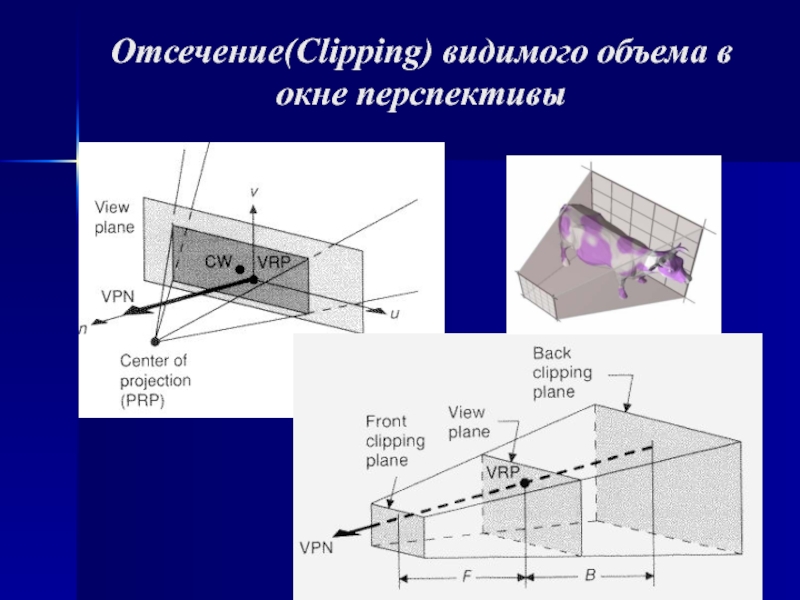
- 4. Отсечение(Clipping) видимого объема в окне перспективы
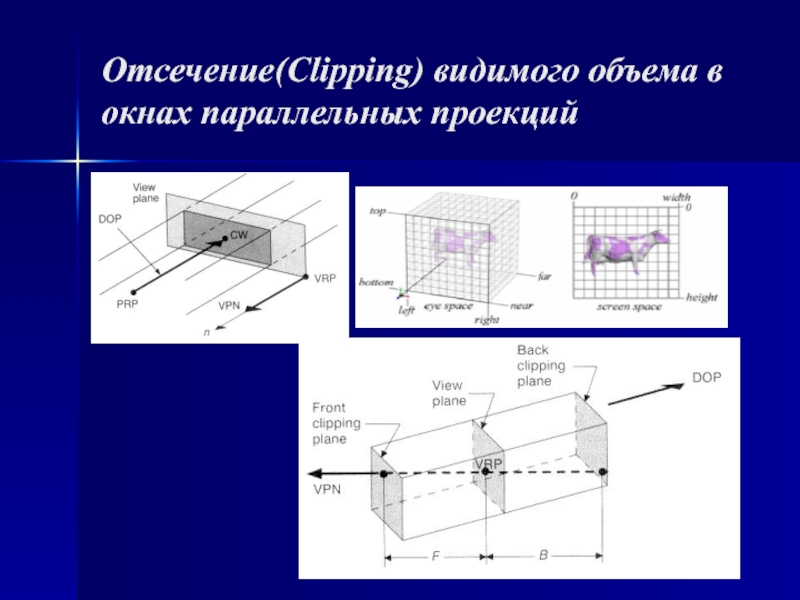
- 5. Отсечение(Clipping) видимого объема в окнах параллельных проекций
- 6. Алгоритмы отсеченияОтсечение 2DОтсечение 3DАлгоритмы отсечения могут быть
- 7. Алгоритм отсечения 2DПлоская сценаОкно вывода – выпуклое,
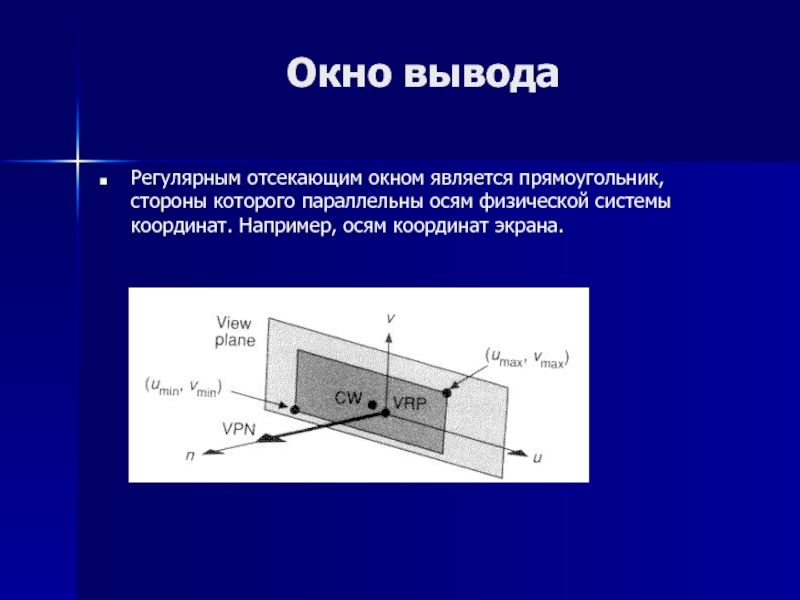
- 8. Окно выводаРегулярным отсекающим окном является прямоугольник, стороны
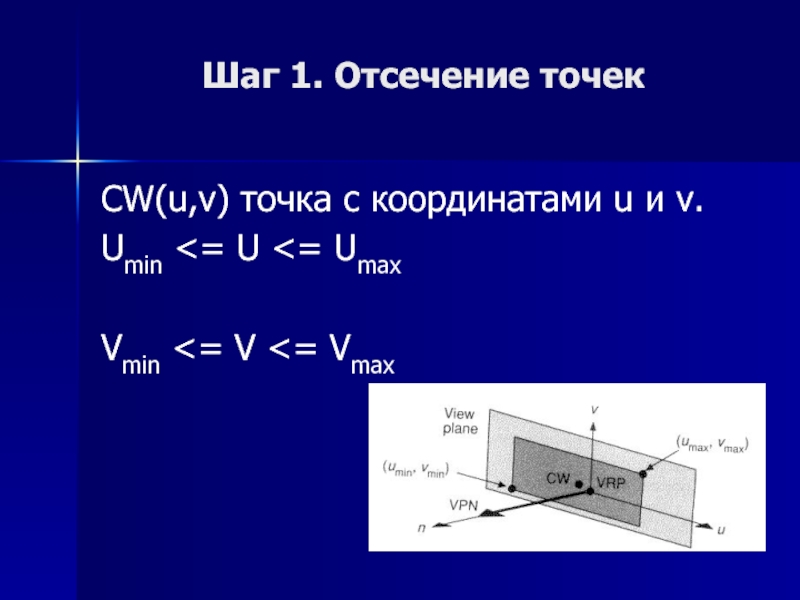
- 9. Шаг 1. Отсечение точекCW(u,v) точка с координатами u и v.Umin
- 10. Шаг 2. Отсечение отрезков. Алгоритм Сазерленда-Коэна
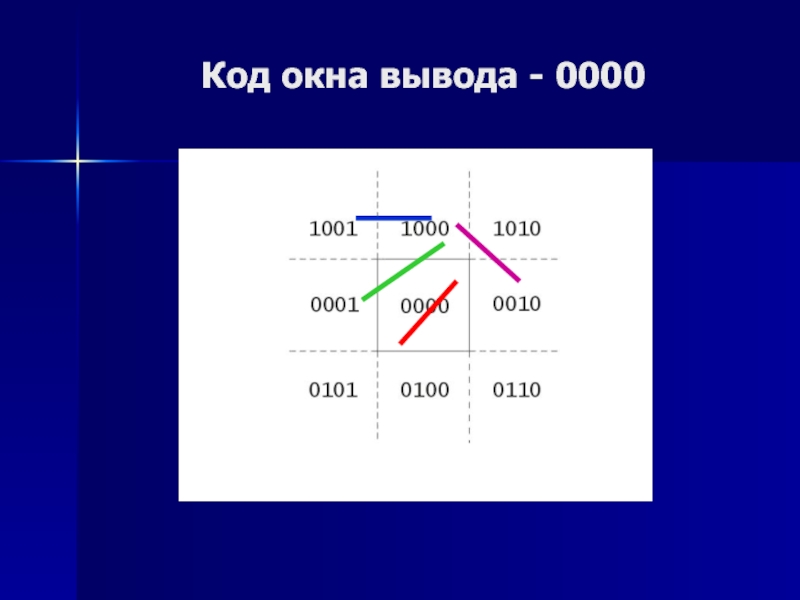
- 11. Код окна вывода - 0000
- 12. Категории отрезков (& - определяется коньюнкция кодов
- 13. Шаг 3. Алгоритм разбиения средней точкой (для
- 14. Алгоритм Сазерленда-Коэна удобен, для отсечения частей изображения значительно выходящих за границы окна вывода
- 15. Отсечение 3d объектов (отсечение по видимому объему)Двумя
- 16. Отсечение в однородных координатахКогда отсечение необходимо провести
- 17. Отсечение многоугольниковПредыдущее обсуждение было связано с отсечением
- 18. Алгоритм Сазерленда-Ходжмена. Отсечение многоугольников.Основная идея алгоритма состоит
- 19. Скачать презентанцию
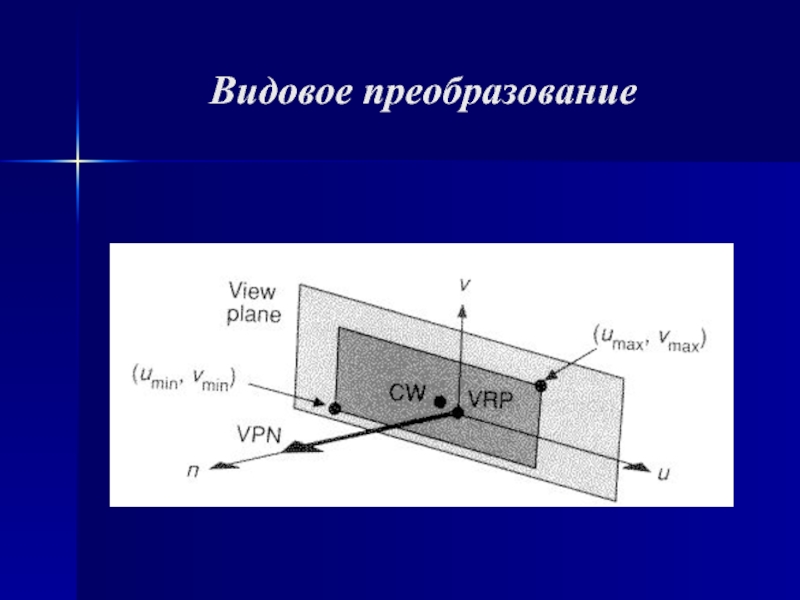
Видовое преобразование
Слайды и текст этой презентации
Слайд 1Отсечение невидимых частей объектов(Clipping) Видимый объем (пирамида\параллелепипед видимости) – выделенная часть
Слайд 6Алгоритмы отсечения
Отсечение 2D
Отсечение 3D
Алгоритмы отсечения могут быть реализованы программно или
аппаратно. Алгоритмы отсечения, реализованные программно, зачастую оказываются недостаточно быстродействующими для
интерактивных графических приложений.Поэтому как 2D, так и 3D алгоритмы отсечения реализуются аппаратными или микропрограммными средствами.
Слайд 7Алгоритм отсечения 2D
Плоская сцена
Окно вывода – выпуклое, регулярной формы
Цель алгоритма
отсечения – определить те точки, отрезки (части отрезков), которые лежат
внутри окна вывода.Эти точки, отрезки (части отрезков) остаются для визуализации, а все остальное отбрасывается.
Слайд 8Окно вывода
Регулярным отсекающим окном является прямоугольник, стороны которого параллельны осям
физической системы координат. Например, осям координат экрана.
Слайд 10Шаг 2. Отсечение отрезков.
Алгоритм Сазерленда-Коэна
Рассмотрим задачу отсечения отрезков прямых.
Некоторые из них полностью лежат внутри области экрана, другие целиком
вне ее, а некоторые пересекают границу экрана.Алгоритм Сазерленда-Коэна позволяет найти полностью видимые и отсекать полностью невидимые отрезки.
Слайд 12Категории отрезков
(& - определяется коньюнкция кодов концов отрезка)
Полностью видимый –
код1 & код2 = 0000.
Тривиально невидимый - код1 & код2
≠ 0000.Неопределенный - код1 ≠ 0000, код2 ≠ 0000,
код1 & код2 = 0000.
Алгоритм работает в пространстве изображений(растровый), т.к. важно свести задачу к двоичному виду(реализовано аппаратно или микропрограммно), а не к решению геометрической задачи поиска точки пересечения отрезков на основе системы линейных уравнений, X=x1 + t(x2-x1)
Y=y1 + t(y2-y1).
Слайд 13Шаг 3. Алгоритм разбиения средней точкой
(для неопределенных отрезков)
Для отрезков, пересекающих
окно вывода, которые нельзя принять за видимые или полностью отбросить.
Последовательно
определяется средняя точка при делении отрезка пополам до тех пор, пока одна из частей отрезка не будет принята целиком(если есть пересечение), а другая часть – целиком отброшена.Максимально необходимое число делений = максимальному числу двоичных разрядов, используемых для представления координат u и v.
Слайд 14Алгоритм Сазерленда-Коэна удобен, для отсечения частей изображения значительно выходящих за
границы окна вывода
Слайд 15Отсечение 3d объектов
(отсечение по видимому объему)
Двумя наиболее распространенными формами видимого
объема являются:
Усеченная пирамида,
Прямоугольный параллелепипед.
Как и 2d отсечении, отрезки, которые полностью
видимы или тривиально невидимы, можно идентифицировать с помощью алгоритма Сазерленда-Коэна. В трехмерном случае используется 6-битный код.
В биты кода заносятся 1 и 0 с помощью обобщения двумерной процедуры.
В случае частичной видимости необходимо определить пересечения отрезка с гранями отсекающего объема
Слайд 16Отсечение в однородных координатах
Когда отсечение необходимо провести в однородной системе
координат, то нужно проявить осторожность, если при этом производится еще
и проецирование. Отрезок может «заворачиваться» в бесконечности так, что внутри видимого объема(если он не ограничен дальней плоскостью) будут видны сразу обе части отрезка.Джим Блинн доказал, что отсечение всех отрезков до завершения процедуры перспективного проецирования(присутствует деление всех координат на на значение однородной координаты), удаляет части отрезков, которые «возвращаются» из бесконечности.
Лианг и Барский получили корректный результат отсечения отрезков в однородной системе координат, используя усеченную пирамиду видимости.
Доказано, что и к отсекающему объему, и к отрезку перед проецированием можно применить любое аффинное преобразование(т.е. повороты, переносы и т.п.)
Слайд 17Отсечение многоугольников
Предыдущее обсуждение было связано с отсечением отрезков. Разумеется, многоугольник
можно рассматривать как набор отрезков.
Однако, если замкнутый многоугольник отсекается, как
набор отрезков, то части исходного объекта могут превратиться в один или более открытых многоугольников.Если многоугольники являются сплошными областями(а не заштрихованными), то необходимо, чтобы замкнутость сохранялась и у результата. Например, отрезки (a,b) и (c,d) должны быть добавлены к описанию видимой части многоугольника.
b
a
d
c
Слайд 18Алгоритм Сазерленда-Ходжмена.
Отсечение многоугольников.
Основная идея алгоритма состоит в том, что отсечь
многоугольник относительно одной прямой легко. Исходный и каждый из промежуточных
многоугольников отсекается последовательно относительно одной прямой(одна из сторон окна видимости).Исходный многоугольник задается списком вершин - P1, P2,…,Pn, который порождает список его ребер - P1 P2,…, Pn-1Pn, PnP1.
Этот алгоритм способен отсекать любой многоугольник, выпуклый\невыпуклый, плоский\неплоский, относительно окна видимости, являющегося выпуклым многоугольником.
Порядок отсечения
многоугольника разными сторонами
окна непринципиален.