Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Параболалық теңдеуге қойылған бастапқы-шеттік есепті Галеркин әдісімен шешу
Содержание
- 1. Параболалық теңдеуге қойылған бастапқы-шеттік есепті Галеркин әдісімен шешу
- 2. МақсатПараболалық теңдеуге қойылған бастапқы-шеттік есепті Галеркин әдісін пайдаланып сандық әдіс арқылы жуық шешімін табу
- 3. Слайд 3
- 4. Thema/ StudentМұндағы
- 5. Thema/ Student D облысында екі рет
- 6. Thema/ tudent(1) теңдеудегі
- 7. Thema/ Student
- 8. Thema/ StudentЖалпы жағдайда Галеркин әдісінде бұл шарттар
- 9. Thema/ Student(7) шартты ашып жазайықнемесе немесе(9)
- 10. Thema/ StudentМұндағы
- 11. Thema/ StudentЕгерде өзіміздің қарауымызға енгізсек, онда (9)
- 12. Thema/ StudentАл, енді (8) ашып жазсақ, онда
- 13. Thema/ StudentМұндағы
- 14. Thema/ StudentОсылайша, (4)-нің сынақ шешімін анықтайтын функцияларын
- 15. Thema/ Student
- 16. Thema/ StudentСызықты параболалық теңдеудің Галеркин әдісі арқылы Math Cad программасындаДәл шешімнің графигіЖуық шешімнің графигі
- 17. Thema/ StudentГалеркин әдісіндегі дәл шешімімен жуық шешімінің графиктері
- 18. 1. А. В. Анкилов, П. А. Вельмисов-Алгоритмы
- 19. Скачать презентанцию
МақсатПараболалық теңдеуге қойылған бастапқы-шеттік есепті Галеркин әдісін пайдаланып сандық әдіс арқылы жуық шешімін табу
Слайды и текст этой презентации
Слайд 2Мақсат
Параболалық теңдеуге қойылған бастапқы-шеттік есепті Галеркин әдісін пайдаланып сандық әдіс
арқылы жуық шешімін табу
Слайд 3
Есептің қойылымы
Жазық облыста
(1)(2)
шеттік шарттарын және (3)
бастапқы шарттарды қанағаттандыратын шешімін табу керек.
Thema/ Student
Слайд 4Thema/ Student
Мұндағы
облысында үзіліссіз функциялар.
берілген нақты сандар және ,
-да туындысымен бірге үзіліссіз және де келесі шарттарды қанағаттандырады
Слайд 5Thema/ Student
D облысында екі рет дифференциалданатын
- сынақ функциялары да сызықты тәуелсіз және
біртекті шеттік
шарттарды қанағаттандырадай аламыз.
(4)
Слайд 6Thema/ tudent
(1) теңдеудегі
функциясын функциясының орнына
қойып,сәйкессіздікті аламыз
немесе
(5)
Слайд 7Thema/ Student
ді (3) бастапқы шартқа қойып,
сәйкессіздігін аламыз.
функциясы және бастапқы мәндерінде
сәйкессіздік қандай да бір мағынада аз болатындай етіп қосымша шарттар береміз .
(6)
Слайд 8Thema/ Student
Жалпы жағдайда Галеркин әдісінде бұл шарттар төмендегі теңдеулер жүйесімен
анықталынады:
(7)(8)
мұндағы -да берілген сызықты тәуелсіз түзілетін функциялар; ал
Слайд 11Thema/ Student
Егерде өзіміздің қарауымызға
енгізсек, онда (9) жүйе матрицалық түрде
жазамыз.
(13)
Енді (13)-дан
(14)аламыз.
Слайд 13Thema/ Student
Мұндағы
(10) формуласы арқылы анықталады, ал
Егер
матрицасын енгізсек, онда (15)-дан (16)
аламыз.
Слайд 14Thema/ Student
Осылайша, (4)-нің сынақ шешімін анықтайтын
функцияларын табу үшін (14)
нормал жүйесінің (16) бастапқы шарттары
бар белгісіз
сызықты жай дифференциалдық теңдеулер жүйесіне қойылған Коши есебін аламыз. Көрсетілген Коши есебін шешіп және осы шешімнен анықталынатын функцияларын (4)-ге қойып, сынақ шешімдерінің құрылуын аяқтаймыз.
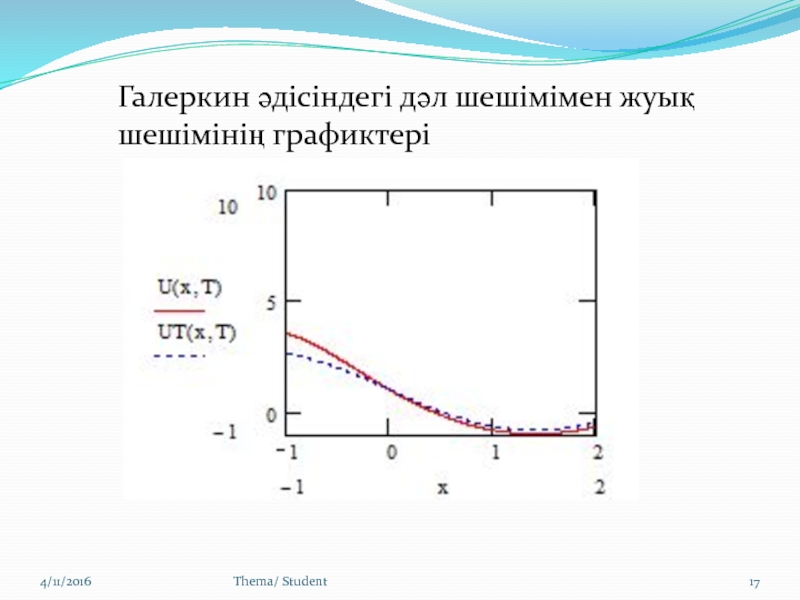
Слайд 16Thema/ Student
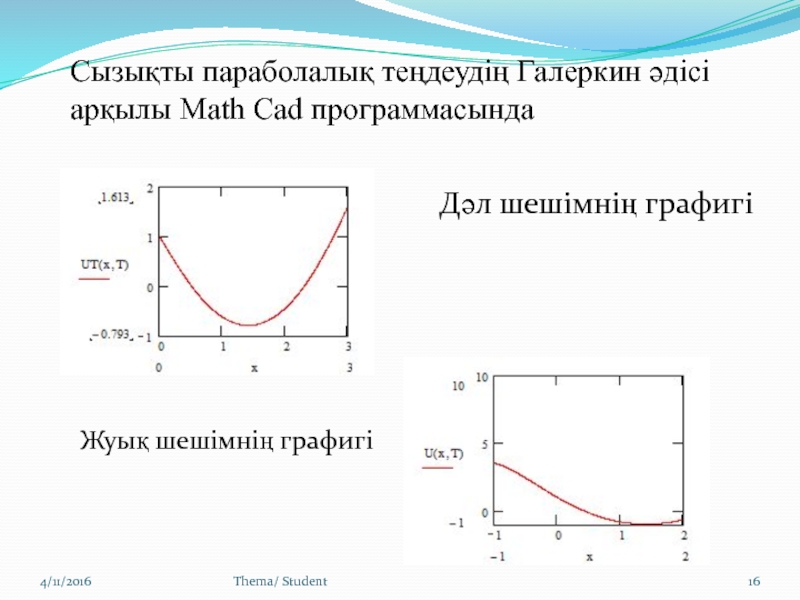
Сызықты параболалық теңдеудің Галеркин әдісі арқылы Math Cad программасында
Дәл
шешімнің графигі
Жуық шешімнің графигі
Слайд 181. А. В. Анкилов, П. А. Вельмисов-Алгоритмы методов взвешенных невязок
в системе MATHCAD
2. С.Ю Игнатович-Метод Галеркина решения линейных граничных задач
для дифференциальных уравнений3. Матвеев Н. М. Дифференциальные уравнения. — Л.: изд-во Ленингр. ун-та, 1965
Пайдаланылған әдебиеттер