Слайд 1Параметрическая модель VaR (Value at Risk)
Слайд 2Предпосылки расчета VaR
VaR можно перевести как стоимость (портфеля), которой рискует
инвестор
Дисперсия не может рассматриваться как подходящий показатель измерения риска портфеля,
т.к. не учитывает возможную скошенность в распределении доходности портфеля, если оно не является симметричным
VaR – это показатель, оценивающий риск портфеля (рыночный риск)
VaR позволяет количественно оценить ожидаемые потери в стоимости портфеля в "нормальных условиях" функционирования рынка
Слайд 3Понятие VaR
VaR – это показатель риска, который показывает, какую максимальную
сумму денег может потерять портфель инвестора в течение определенного периода
времени с заданной доверительной вероятностью.
VaR также говорит о том, что потери в стоимости портфеля в течение этого периода времени будут меньше данной величины с определенной вероятностью.
Доверительную вероятность можно определить как показатель, говорящий о том, какое количество раз из каждых 100 раз потери в стоимости портфеля не превысят данного уровня. Уровень доверительной вероятности задается заранее и зависит от характера компании, владеющей портфелем, и от субъективного подхода управляющего портфелем к этому вопросу. Обычно он равен 95% или 99%.
Слайд 4Предположения для расчета VaR
При расчете VaR для некоторого временного интервала
предполагается, что состав портфеля за этот период остается неизменным.
В
противном случае необходимо пересчитывать и значение VaR, т.к. новые активы, включаемые в портфель, изменяют и его риск
Слайд 5Период для расчета VaR
Наиболее распространенный период, для которого рассчитывается VaR,
– один день, т.е. 24 часа. Однодневный VaR обозначают как
DEaR (Daily Earning at Risk).
Базельский банк международных расчетов рекомендует банкам рассчитывать 10-дневный VaR с доверительной вероятностью 99% для определения минимального уровня собственных средств.
Чем больше период времени, для которого рассчитывается VaR, тем больше будет и его величина, т.к. на более длительном отрезке времени возрастает и вероятность более крупных потерь
Слайд 6Понятия абсолютного и относительного значения VaR
Абсолютный VaR можно определить как
максимальную сумму денег, которую может потерять портфель инвестора в течение
определенного периода времени с заданной доверительной вероятностью.
Относительный VaR отличается от абсолютного тем, что он рассчитывается относительно ожидаемой доходности портфеля. Его значение учитывает, что инвестор с заданной вероятностью не только может потерять сумму равную абсолютному VaR, но и не получить сумму равную средней ожидаемой доходности портфеля за рассматриваемый период.
Если ожидаемая доходность портфеля равна нулю, то значения абсолютного и относительного VaR совпадают
Слайд 7Методики определения VaR
параметрические модели (аналитическими или дисперсионно-ковариационными)
непараметрические модели
Слайд 8Параметрическая модель VaR
Модель называется параметрической, если нам известна функция распределения
случайной величины и параметры ее распределения.
В параметрической модели VaR
предполагается, что доходность финансовых активов следует определенному виду вероятностного распределения, обычно нормального.
Для заданного уровня доверительной вероятности VaR портфеля рассчитывают по формуле:
Слайд 9Параметрическая модель VaR
Для заданного уровня доверительной вероятности VaR портфеля рассчитывают
по формуле:
- стоимость портфеля
- риск портфеля (стандартное отклонение доходности портфеля)
- квантиль уровня α нормального распределения
Слайд 10Матричная форма расчета VaR
V – матрица-столбец значений VaR по каждой
бумаге;
VT – транспонированная матрица-столбец значений VaR по каждой бумаге, т.е.
матрица-строка;
ρ – корреляционная матрица размерности nхn (n – число активов в портфеле).
Слайд 11Диверсифицированный и недиверсифицированный VaR портфеля
Поскольку корреляции могут изменяться со временем,
то наряду с показателем диверсифицированного VaR целесообразно рассчитывать и не
диверсифицированный VaR.
VaR с учетом корреляций между активами портфеля называют диверсифицированным.
Если определить VaR без учета корреляций, то получим не диверсифицированный VaR. Он представляет собой простую сумму индивидуальных VaR активов портфеля и покажет максимум возможных потерь (при нормальных условиях рынка) для данного уровня доверительной вероятности в случае неустойчивости корреляций или ошибки их оценок
Слайд 12Расчет VaR с учетом временного интервала
Для расчета однодневного VaR при
данных за год матрицу ковариаций, составленную из годичных значений, необходимо
перевести в матрицу с однодневными значениями.
Данную матрицу удобно сразу скорректировать в соответствии с заданным уровнем доверительной вероятности.
Тогда годичную матрицу ковариаций следует умножить на коэффициент:
Слайд 13Расчет VaR портфеля через стоимости активов
Слайд 14Расчет VaR портфеля из двух активов
Пусть стандартные отклонения и уд.
веса первого и второго активов соответственно равны σ1, θ1 и
σ2, θ2, стоимость портфеля составляет Р.
Тогда VaR портфеля для уровня доверительной вероятности α равен:
или
или
Слайд 15Расчет VaR портфеля из двух активов
Если коэффициент корреляции между доходностями
активов равен единице
Тогда VaR портфеля для уровня доверительной вероятности α
равен:
или
В случае полной положительной корреляции между активами VaR портфеля является суммой индивидуальных VaR входящих в него активов.
Слайд 16Перерасчет значения VaR для разных значений доверительной вероятности
Пусть VaR портфеля
для доверительной вероятности z1 равен:
для доверительной вероятности z2:
Выразим значение Р из
первой формулы и подставим во вторую формулу:
Слайд 17Перерасчет значения VaR для разных периодов времени
Пусть VaR портфеля для
периода t1 равен:
для периода t2:
Выразим значение Pσz из первой формулы
и подставим
во вторую:
Таким образом, зная величину VaR1 для периода времени t1, легко получить VaR2 для периода времени t2.
Слайд 18Пример 1
Определить однодневный VaR с доверительной вероятностью 95% для портфеля
стоимостью 10 млн. руб., в который входят акции только одной
компании. Стандартное отклонение доходности акции в расчете на год равно 25%. В году 250 торговых дней.
В предположении, что на основании данных за прошлый год средняя доходность портфеля за день составляла 0,1% рассчитать относительный VaR.
Слайд 19Решение примера 1
Так как необходимо определить однодневный VаR, то вначале
рассчитаем стандартное отклонение доходности акции для одного дня
По таблице нормального
распределения (функция Лапласа) находим, что уровню доверительной вероятности в 95% соответствует 1,65 стандартных отклонений. VaR портфеля равен
Слайд 20Выводы (интерпретация результата)
Таким образом, в течение следующих 24 часов максимальные
потери в стоимости портфеля инвестора с доверительной вероятностью 95% могут
составить 260,7 тыс. руб.
В течение следующих 24 часов вероятность потерять сумму денег меньше 260,7 тыс. руб. равна 95%, а сумму больше 260,7 тыс. руб. – 5%.
Слайд 21Расчет относительного VaR
Т.к. за прошлый год средняя доходность портфеля за
день составляла 0,1%, то от 10 млн. руб. это составляет
10 тыс. руб. Тогда относительный VaR равен:
Слайд 22Пример 2
Определить однодневный VaR с доверительной вероятностью 95% для портфеля
стоимостью 10 млн. руб., в который входят акции двух компаний.
Уд. вес первой акции в стоимости портфеля составляет 60%, второй – 40%. Стандартное отклонение доходности первой акции в расчете на один день равно 1,58%, второй – 1,9%, коэффициент корреляции доходностей акций равен 0,8.
Слайд 23Решение примера 2
Определяем стандартное отклонение доходности портфеля:
По таблице нормального распределения
(функция Лапласа) находим, что уровню доверительной вероятности в 95% соответствует
1,65 стандартных отклонений. Определяем VaR портфеля
Слайд 242 способ расчета VaR
Определим в примере 2 абсолютный VaR для
первой акции:
Абсолютный VaR для второй акции равен:
Абсолютный VaR портфеля составляет:
Слайд 25Пример 3
Российский инвестор купил акции компании А на 147,059 тыс.
долл. Стандартное отклонение доходности акции составляет 1,58%. Курс доллара 1долл.=68
руб., стандартное отклонение валютного курса в расчете на один день 0,6%, коэффициент корреляции между курсом доллара и ценой акции компании А равен 0,2. Определить VaR портфеля инвестора с доверительной вероятностью 95%.
Слайд 26Решение примера 3
Текущий курс доллара равен 68 руб., поэтому рублевый
эквивалент позиции инвестора составляет:
147,059 тыс.дол.∙68руб.=10 млн.руб.
Это означает, что в настоящий
момент инвестор рискует суммой в 10 млн. руб., и данный риск обусловлен двумя факторами: возможным падением котировок акций компании А и падением курса доллара. Реализация любого из данных рисков приведет к падению стоимости портфеля ниже суммы в 10 млн. руб.
Слайд 27Решение примера 3
Т.к. цена акций компании А и валютный курс
имеют корреляцию существенно меньшую чем плюс один, то общий риск
портфеля уменьшается за счет эффекта диверсификации. Поэтому дисперсия доходности портфеля равна:
Стандартное отклонение доходности составляет:
Однодневный VaR портфеля равен:
Слайд 28Пример 4
Курс доллара составляет 1долл.=68 руб., курс евро – 1евро=74
руб. Банк купил на спотовом рынке 147,059 тыс. долл. и
осуществил короткую продажу 135,135 тыс. евро. Стандартное отклонение курса доллара в расчете на один день составляет 0,6%, евро – 0,65%, коэффициент корреляции равен 0,85. Определить однодневный VaR портфеля с доверительной вероятностью 95%.
Слайд 29Решение примера 4
Рассчитаем VaR в рублях, так как банк закроет
свои позиции в иностранных валютах, конвертировав их в рубли.
Долларовая
позиция банка в рублях составляет:
147,059 тыс.дол.∙68руб.=10 млн.руб.
Позиция по евро в рублях:
135,135 тыс.дол.∙74руб.=10 млн.руб.
Поскольку банк продал евро, то для дальнейших расчетов его позицию следует записать со знаком минус, т.е. –10млн.руб.
Слайд 30Решение примера 4
VaR по долларовой позиции равен:
VaR по евро равен:
VaR
портфеля составляет:
Слайд 31Оценка ошибки параметрической модели VaR
Слайд 32VaR портфеля рассчитывается на основе выборочных данных за определенный период
времени.
В результате возникает необходимость оценить доверительный интервал для полученного
значения VaR
По данным статистики мы определяем не истинное, а "исправленное" стандартное отклонение. В связи с этим, прежде всего, следует найти доверительный интервал для стандартного отклонения доходности портфеля.
Слайд 33«Исправленная» дисперсия
Доходность портфеля имеет нормальное распределение. Наилучшей оценкой дисперсии нормального
распределения является "исправленная" дисперсия:
Слайд 34Получение доверительного интервала для VaR
Разделим обе части равенства на истинную
дисперсию σ2 случайной величины
Величина
имеет распределение хи-квадрат (χ²) с n-1 степенями свободы.
Слайд 35Доверительный интервал
Необходимо найти границы интервала, который бы с вероятностью γ
накрывал истинное значение дисперсии случайной величины
Слайд 36Доверительный интервал
Значения конечных точек доверительного интервала обычно выбирают таким образом,
чтобы вероятности событий χ ² < χ 1² и χ²
> χ2² были одинаковыми.
Пусть эта вероятность равна α. Тогда
Слайд 37Доверительный интервал для VaR портфеля
По таблице квантилей распределения χ² находим
нижнюю и верхнюю границы доверительного интервала дисперсии случайной величины. Квадратные
корни из данных значений представляют собой нижнюю и верхнюю границы доверительного интервала стандартного отклонения.
Если в качестве случайной величины выступает доходность портфеля, то найденные значения сигм показывают доверительные границы стандартного отклонения доходности портфеля.
Слайд 38Доверительный интервал для VaR портфеля
На основе полученных данных рассчитаем доверительный
интервал для VaR портфеля по формулам
Слайд 39Пример 5
В примере 2 был получен однодневный VaR портфеля из
двух акций в 267,3 тыс. руб.
Пусть данный результат был
получен на основе данных по доходности акций за 101 день. Требуется определить доверительный интервал для VaR с доверительной вероятностью γ = 0,95.
Слайд 40Решение примера 5
Из соотношения γ = 1 – 2α находим
значение α, соответствующее доверительной вероятности 95%:
Количество наблюдений случайной величины составило
n=101 день. Поэтому количество степеней свободы в примере равно n – 1 = 100.
По таблице квантилей распределения χ² находим квантили χ²1-α и χ²α со степенями свободы 100:
χ²0,975 =129,56; χ²0,025 =74,22.
Слайд 41Решение примера 5
Нижняя граница доверительного интервала для дисперсии равна:
для стандартного
отклонения
Верхняя граница доверительного интервала для дисперсии равна:
для стандартного отклонения
Слайд 42Решение примера 5
Находим нижнюю и верхнюю границы доверительного интервала для
VaR портфеля:
Таким образом, с доверительной вероятностью 95% можно быть уверенным,
что действительное значение VaR лежит в границах от 237,6 тыс. руб. до 310,2 тыс. руб.
Слайд 43Ожидаемые потери портфеля в случае превышения значения VaR
Слайд 44Средние ожидаемые потери
Показатель средних ожидаемых потерь (expected shortfall) показывает величину
средних потерь для данного уровня доверительной вероятности и периода времени
в случае, если убытки превысят значение VaR.
Показатель средних ожидаемых потерь представляет собой условное математическое ожидание потерь при условии, что их величина оказалась больше значения VaR.
Слайд 45Условная вероятность
Условная вероятность наступления события В при условии, что произошло
событие A, равна:
Слайд 46Средние ожидаемые потери
Для непрерывной случайной величины X, характеризующей убытки и
доходы портфеля, можно записать:
Слайд 47Средние ожидаемые потери
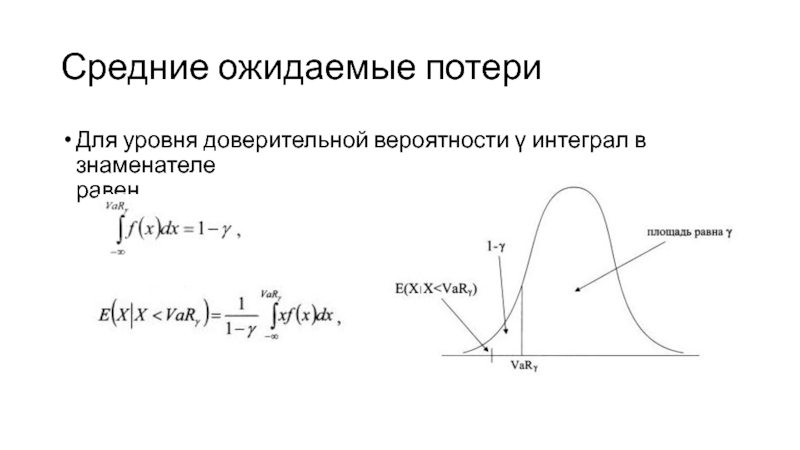
Для уровня доверительной вероятности γ интеграл в знаменателе
равен
Слайд 48Средние ожидаемые потери для нормального распределения
Пусть случайная величина X имеет
нормальное распределение со средним значением равным нулю и стандартным отклонением
σ. Тогда ее плотность вероятности принимает вид:
Тогда средние ожидаемые потери равны
Слайд 49Величина средних ожидаемых потерь
При условии
Слайд 51Понятие EaR
Противоположным понятием по отношению к VaR является EaR (Earnings
at Risk).
EaR показывает, какую максимальную сумму дохода может принести
портфель инвестора в течение определенного периода времени с заданной доверительной вероятностью.
Если доходность портфеля имеет нормальное распределение, и ее среднее значение равно нулю, то показатель EaR будет равен показателю VaR по абсолютной величине.
Слайд 52Пример 6
Пусть стоимость портфеля инвестора составляет 100 млн. руб., EaR
для одного дня равен 2 млн. руб. с доверительной вероятностью
95%.
Данную информацию можно интерпретировать следующим образом:
вероятность того, что в течение следующих 24 часов доход инвестора составит меньше 2 млн. руб. равна 95%,
вероятность того, что в течение следующих 24 часов его доход превысит 2 млн. руб. равна 5%,
инвестор вправе ожидать, что в среднем его доход в течение 95 дней из каждых 100 дней не превысит 2 млн. руб., или что он окажется больше 2 млн. руб. в течение 5 дней из каждых 100 дней.
Слайд 53Замечание
При выборе портфеля можно руководствоваться показателем, который определяется как
отношение EaR к VaR.
Чем больше значение этого коэффициента для
данного уровня доверительной вероятности, тем предпочтительнее портфель, поскольку он предлагает большие возможные выигрыши в сравнении с потерями.
Он также может служить мерой оценки скошенности потенциальных результатов доходности портфеля для данного уровня доверительной вероятности