углом.
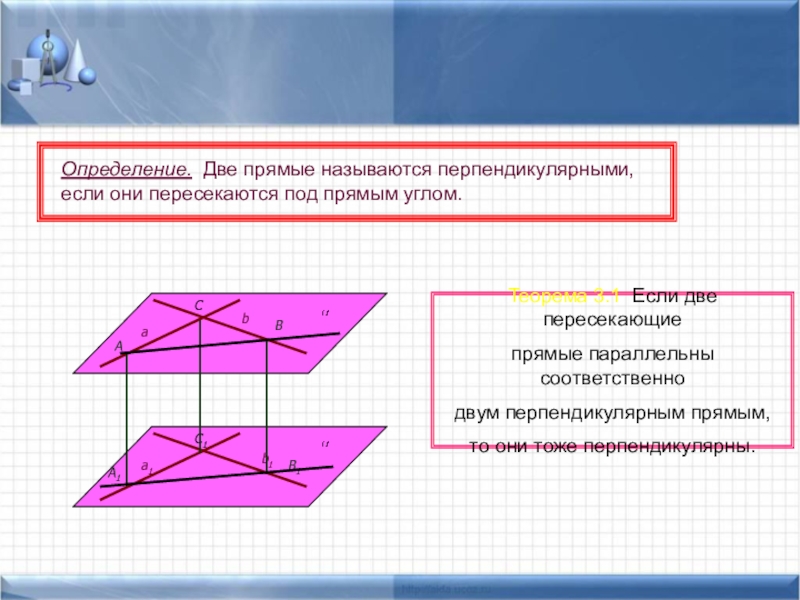
Теорема 3.1 Если две пересекающие
прямые параллельны соответственно
двум перпендикулярным
прямым, то они тоже перпендикулярны.
a
b
a1
b1
C
C1
A
A1
B
B1