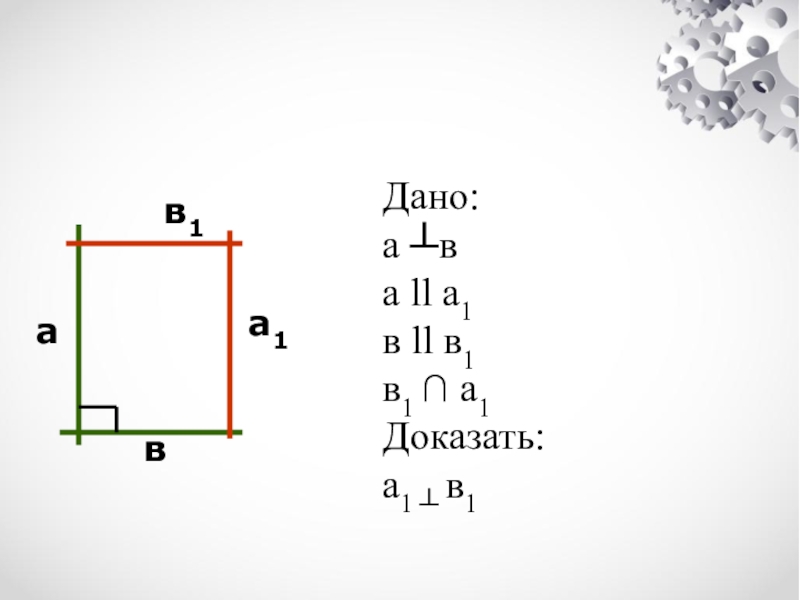
определение пересекающихся, параллельных, скрещивающихся прямых.
3. Перечислите случаи расположения прямой и
плоскости в пространстве.4. Дайте определение пересекающихся, параллельных прямой и плоскости.
5. Перечислите случаи расположения плоскостей в пространстве.
6. Дайте определение пересекающихся, параллельных плоскостей.