Первое начало термодинамики В диффененциальной форме d обозначение

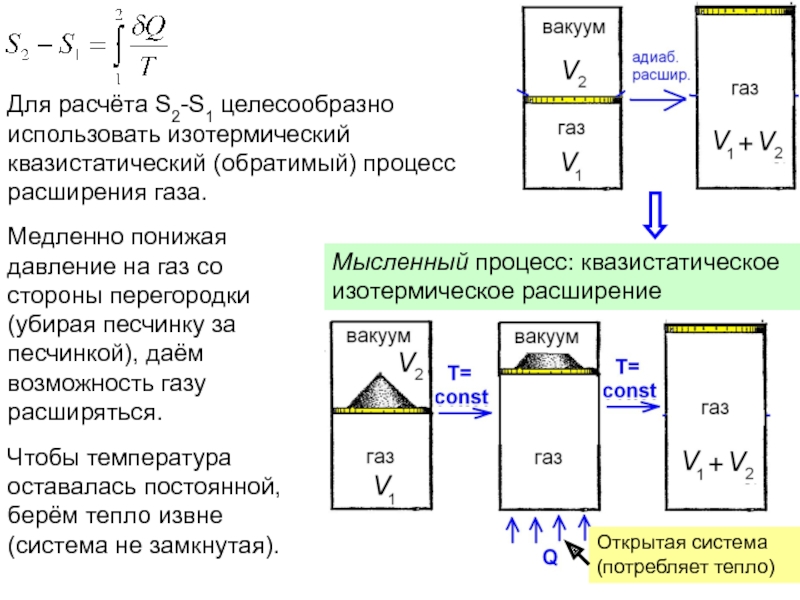
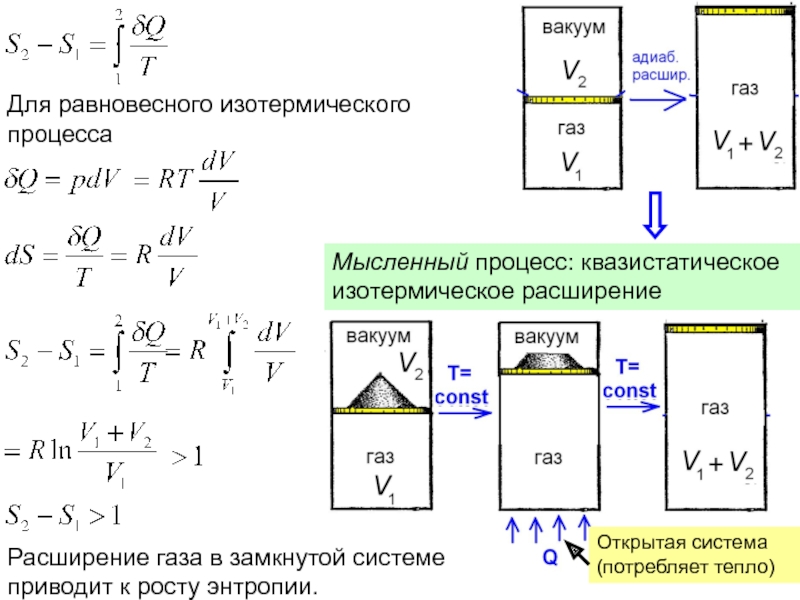
функций состояния
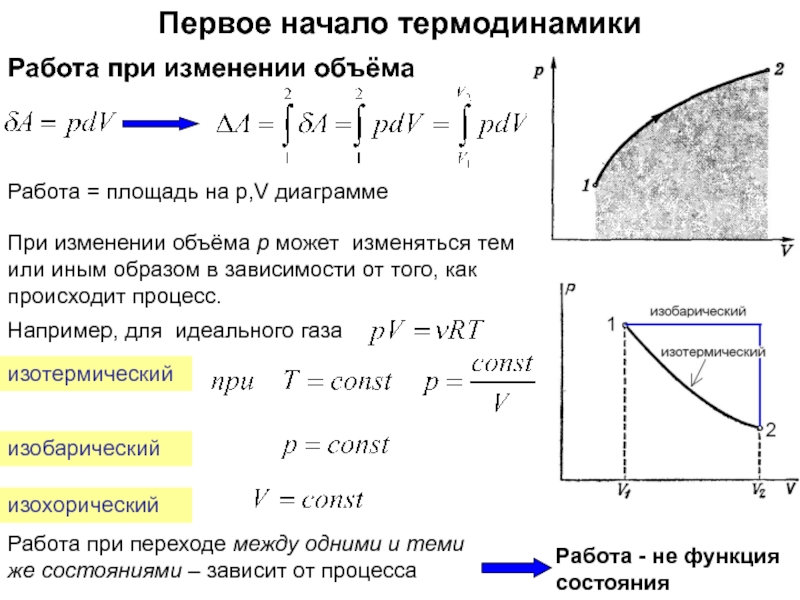
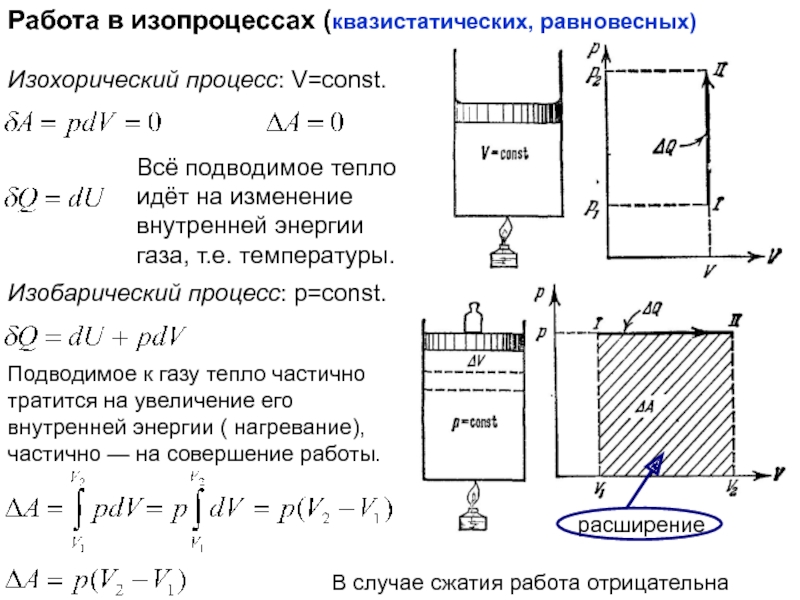
Работа при изменении объёма
«δ» обозначение бесконечно малых в

случае, когда функция не является функцией состояния.

dV – приращение объёма макросистемы (например, газа)

p – давление оказываемое на соседние тела (стенки)

Элементарная работа сил, действующих со стороны газа на стенки

δA=Fdh

не функции состояния

=pSdh

=pdV

С учётом выражения для работы при изменении объёма первое начало термодинамики может быт записано в форме

диаграмме
При изменении объёма p может изменяться тем или иным образом

в зависимости от того, как происходит процесс.

Например, для идеального газа

изотермический

изобарический

Работа при переходе между одними и теми же состояниями – зависит от процесса

Работа - не функция состояния

изохорический

которого система возвращается в исходное состояние, то такой процесс называется

круговым процессом, или циклом.

На диаграмме p,V такой процесс имеет вид замкнутой кривой.

Работа совершаемая за цикл, численно равна площади внутри цикла

Если точка, изображающая состояние системы, описывает цикл
по часовой стрелке, то работа системы положительна (ΔA>0),
если против часовой стрелки, то ΔA<0

не функция состояния
Поскольку внутренняя энергия U является функцией состояния, а

работа нет (работа – функция процесса), из первого начала следует, что и количество теплоты Q не является функцией состояния (теплота – функция процесса).

Поэтому δQ

сообщить 1 молю газа, чтобы повысить его температуру на 1

градус Кельвина:

С – функция процесса (как и Q).

Наиболее важны теплоёмкости для процессов проводимых при постоянном объёме CV и при постоянном давлении Cp.

Теплоёмкость при постоянном объёме (dV = 0).

Всё подводимое тепло идёт на изменение внутренней энергии газа, т.е. его температуры.

идёт не только на изменение внутренней энергии газа, но и

на совершение работы.

Формула Майера

Постоянная адиабаты:

теории идеального газа средняя энергия поступательного движения молекул
Одноатомный идеальный газ

– атомы двигаются только поступательно.

Внутренняя энергия 1 моля одноатомного газа

Теплоёмкость одноатомного газа

Одноатомный идеальный газ

газ
Больцман: гипотеза о равном распределении средней энергии молекул по степеням

свободы.

Степени свободы

Три поступательные степени свободы

+ две вращательные степени свободы, если молекула – жёсткая гантель.

Жесткая двухатомная молекула: 5 степеней свободы

Если молекула упругая, то возможны колебания атомов – появляется ещё колебательная степень свободы.

Гипотеза о равнораспределении по степеням свободы.

Тот факт, что средняя энергия поступательного движения равна 3/2kT, означает, что на одну степень свободы приходится энергия kT/2.

газ
Больцман: гипотеза о равном распределении средней энергии молекул по степеням

свободы.

Гипотеза о равнораспределении по степеням свободы.

При этом на колебательную степень свободы приходится две половинки kT – одна на кинетическую энергию и одна на потенциальную.

Итак, средняя энергия молекулы

где i – число степеней свободы

Для жёсткой двухатомной молекулы

Для упругой двухатомной молекулы

моля двухатомного газа
Молярная теплоёмкость идеального двухатомного газа
При этом непонятное поведение

при низких и высоких Т.

Одна из основных проблем классической физики.

Одноатомный газ – прекрасное совпадение с теорией при всех Т.

Что даёт эксперимент?

Двухатомный газ - в области средних Т, включая комнатную, Сv ≈ 5/2 R. Хорошее совпадение с моделью молекулы в виде жёсткой гантели (но почему она жёсткая?).

идёт на изменение внутренней энергии газа, т.е. температуры.
Изобарический процесс: p=const.

Подводимое к газу тепло частично тратится на увеличение его внутренней энергии ( нагревание), частично — на совершение работы.

В случае сжатия работа отрицательна

= const
U = const
Подводимое к газу при изотермическом расширении тепло

целиком превращается в работу расширения.

протекающий при отсутствии теплообмена с окружающими телами.
Согласно первому началу
При адиабатическом

расширении работа совершается газом за счет уменьшения его внутренней энергии, газ охлаждается

Для нахождения работы как функции p и V получим уравнение адиабаты.

При адиабатическом сжатии над газом совершается работа, которая целиком идёт на приращение внутренней энергии газа, газ нагревается

уравнения

газ охлаждается и поэтому давление ниже, чем в случае изотермического

расширения

При адиабатическом сжатии газ нагревается и поэтому давление выше, чем в случае изотермического сжатия

Нагревание при адиабатическом сжатии используется для воспламенения в дизельных двигателях.

газов через сопла реактивных двигателей процесс расширения газа протекает настолько

быстро, что его можно считать практически адиабатическим.

Работа в адиабатическом процессе

Работа в изопроцессах

тепловых процессов. Энергия теплового движения молекул качественно отличается от всех

других видов энергии – механической, электрической, химической и т. д. Энергия любого вида, кроме энергии теплового движения молекул, может полностью превратиться в любой другой вид энергии, в том числе и в энергию теплового движения. Последняя может испытать превращение в любой другой вид энергии лишь частично (Здесь вопрос с изотермическим изменением объёма, наверное полная обратимость там лишь для бесконечно медленного процесса). Поэтому любой физический процесс, в котором происходит превращение какого-либо вида энергии в энергию теплового движения молекул, является необратимым процессом, т. е. он не может быть осуществлен полностью в обратном направлении.

Первое начало термодинамики – это обобщение закона сохранения энергии на тепловые процессы.

Оказывается, однако, что не все процессы разрешённые первым началом термодинамики возможны. Второе начало термодинамики формулирует эти ограничения.

двигатель с КПД η=1, или невозможен вечный двигатель 2-го рода.

в работу всё тепло, извлекаемое из окружающих тел.
Если бы

тепловой двигатель с КПД =1 был возможен, т.е. если бы всё тепло могло превращаться в работу (Q2=0), мы не нуждались бы в более холодных телах и могли бы совершать работу за счёт отбора тепла из окружающих нас тел, например, от океана. В силу практической безграничности такого источника тепловой энергии это был бы вечный двигатель (второго рода).

Второе начало термодинамики

характеристикой необратимости процессов.
Понятие энтропии играет важную роль не только в

физике, но и в теории информации.

Рудольф Клаузиус
1822-1888

           ,

Можно доказать,. что энтропия (или «приведённое тепло») является функцией состояния (несмотря на то что количество теплоты функцией состояния не является.

Энтропия вводится через её изменение (как часто делается в физике). В дифференциальной форме

Изменение энтропии при переходе системы из состояния 1 в состояние 2 в равновесном процессе

S2 – S1 не зависит от вида процесса. S2 – S1 определяется лишь начальным и конечным состояниями.

где δQ/T относится к квазистатическим процессам.

только разность энтропий для разных состояний системы, но не саму

величину энтропии.

Энтропия определяется с точностью до постоянной.

Однако, используя третье начало термодинамики (теорема Нернста), согласно которому энтропия любой системы при температуре абсолютного нуля равна 0, можно найти и величину самой энтропии.

Второе начало термодинамики

Энтропия

уменьшается – она либо возрастает, либо остаётся постоянной.
В замкнутых системах:
Ещё

одна формулировка 2-го начала

В случае обратимых процессов энтропия замкнутой макросистемы не меняется

В случае необратимых процессов энтропия замкнутой макросистемы возрастает

Таким образом, величина возрастания энтропии в замкнутой системе может служить мерой необратимости процессов, протекающих в системе.

Анализ изменения энтропии даёт указание, в каком направлении могут происходить самопроизвольные необратимые процессы в замкнутой системе: в сторону возрастания энтропии.

теплоизолированных сосуда разделённых перегородкой с вентилем.
Равновесное состояние 1. В

сосуде 1 находится 1 моль идеального газа. В сосуде 2 – вакуум.

После того как вентиль открыли газ адиабатически расширился и заполнил объём 2. После того как давление и температура уравнялась образовалось равновесное состояние 2.

Переход очевидно необратимый. Должно быть S2-S1>0. Проверим.

Энтропия функция состояния. S2-S1 не зависит от пути перехода. Поэтому выберем такой путь на котором легче найти S2-S1.

Поскольку переход был адиабатический и работа не совершалась внутренняя энергия газа не изменилась, следовательно температура в равновесных состояниях 1 и 2 одна и та же.

Будем очень медленно понижать давление на газ со стороны перегородки

и давать ей сдвигаться и брать тепло извне что бы температура оставалась постоянной. Теперь система не является замкнутой и хотя процесс обратимый, энтропия может измениться.

теплоизолированных объёма, разделённых перегородкой.
Равновесное состояние 1:
в объёме V1

находится 1 моль идеального газа, в объёме V2 – вакуум.

Равновесное состояние 2: в объёме V1 находится 1 моль идеального газа,

Необратимый процесс: газ адиабатически расширился и заполнил объём V2.

Переход очевидно необратимый. Должно быть S2-S1>0. Проверим.

1 и 2.
Переход адиабатический,
работа не совершалась (расширение в вакуум,

крышка невесома).

Выберем такой процесс на котором легче найти S2-S1.

Заметим:

Внутренняя энергия газа в состоянии 2 не изменилась.

Температура в равновесных состояниях 1 и 2 одна и та же.

Для расчёта S2-S1 целесообразно использовать изотермический квазистатический процесс.

целесообразно использовать изотермический квазистатический (обратимый) процесс расширения газа.
Медленно понижая

давление на газ со стороны перегородки (убирая песчинку за песчинкой), даём возможность газу расширяться.

Чтобы температура оставалась постоянной, берём тепло извне (система не замкнутая).

процесса
Расширение газа в замкнутой системе приводит к росту энтропии.

началу (в замкнутых системах

) расширение газа в замкнутой системе – необратимый процесс.

Самопроизвольно он может протекать лишь в одну сторону.

Обратный процесс (самопроизвольное сжатие) запрещён вторым началом (поскольку энтропия при этом снижается).

Таким образом, анализ изменения энтропии указывает, какие неравновесные процессы в замкнутой системе возможны (протекают самопроизвольно), а какие нет.

закона. Здесь про энергию мирового океана по Фришу. Если кпд

использования тепла = 1, то холодильник не нужен (тепло не надо отдавать).

Вводится энтропия (по Иродову) как некое открытие, которое даёт меру всем этим необратимостям и формулировка второго начала через энтропию – опять таки как эмпирический закон (можно дать примеры и обобщить – см мои примечания в Иродове pdf).

Теорема Карно и её доказательство с помощью диаграммы T-S - Иродов

Про энтропию по Иродову – энтропия идеального газа и пр

Другие тепловые циклы - Иродов

Статистическая трактовка – Иродов, Зисман

из формулировки Клаузиуса. Действительно, что бы совершить работу в циклическом

процессе надо иметь резервуар с более низкой Т. В него перейдёт часть тепла. Если бы можно было это тепло вернуть (т.е. Без совершения работы передать его более горячему телу), то ВСЁ тепло превратилось бы в работу. Можно и так. Если возможно ВСЁ переданное таким образом тепло превратить в работу тогда внутренняя энергия холодильника не изменится и от океана можно брать энергию. А если часть этого тепла остаётся в холодильнике, то он нагревается и по этой причине нельзя взять энергию от океана.

http://www.physics.ru/courses/op25part1/content/chapter3/section/paragraph12/theory.html
Второй закон термодинамики непосредственно связан с необратимостью реальных тепловых процессов. Энергия теплового движения молекул качественно отличается от всех других видов энергии – механической, электрической, химической и т. д. Энергия любого вида, кроме энергии теплового движения молекул, может полностью превратиться в любой другой вид энергии, в том числе и в энергию теплового движения. Последняя может испытать превращение в любой другой вид энергии лишь частично (Здесь вопрос с изотермическим изменением объёма, наверное полная обратимость там лишь для бесконечно медленного процесса). Поэтому любой физический процесс, в котором происходит превращение какого-либо вида энергии в энергию теплового движения молекул, является необратимым процессом, т. е. он не может быть осуществлен полностью в обратном направлении.

в термодинамически неравновесной системе и в результате этих процессов замкнутая

система приближается к состоянию термодинамического равновесия.
На основании любой из формулировок второго закона термодинамики могут быть доказаны следующие утверждения, которые называются теоремами Карно:
Коэффициент полезного действия тепловой машины, работающей при данных значениях температур нагревателя и холодильника, не может быть больше, чем коэффициент полезного действия машины, работающей по обратимому циклу Карно при тех же значениях температур нагревателя и холодильника.
Коэффициент полезного действия тепловой машины, работающей по циклу Карно, не зависит от рода рабочего тела, а только от температур нагревателя и холодильника.
Таким образом, коэффициент полезного действия машины, работающей по циклу Карно, максимален.

закон возрастания S и даётся вероятностная трактовка. Всё крайне кратко!

машина, которая извлекала бы тепло из океана и превращала бы

его работу.

http://www.physics.ru/courses/op25part1/content/chapter3/section/paragraph12/theory.html
Кельвин (1851): В циклически действующей тепловой машине невозможен процесс, единственным результатом которого было бы преобразование в механическую работу всего количества теплоты, полученного от единственного теплового резервуара (А что если не всего, а хотя бы части, чем это плохо?).
Гипотетическую тепловую машину, в которой мог бы происходить такой процесс, называют вечным двигателем второго рода. В земных условиях такая машина могла бы отбирать тепловую энергию, например, у Мирового океана и полностью превращать ее в работу. Масса воды в Мировом океане составляет примерно 1021 кг, и при ее охлаждении на один градус выделилось бы огромное количество энергии (≈ 1024 Дж), эквивалентное полному сжиганию 1017 кг угля. Ежегодно вырабатываемая на Земле энергия приблизительно в 104 раз меньше. Поэтому вечный двигатель второго рода был бы для человечества не менее привлекателен, чем вечный двигатель первого рода, запрещенный первым законом термодинамики.

То что в работу при циклическом процессе можно преобразовать лишь часть полученного тепла - это понятно и составляет суть второго начала. Но если это тепло дармовое (океан) то всё таки получается что вечный двигатель возможен.