Планиметрия Равенство и подобие треугольников

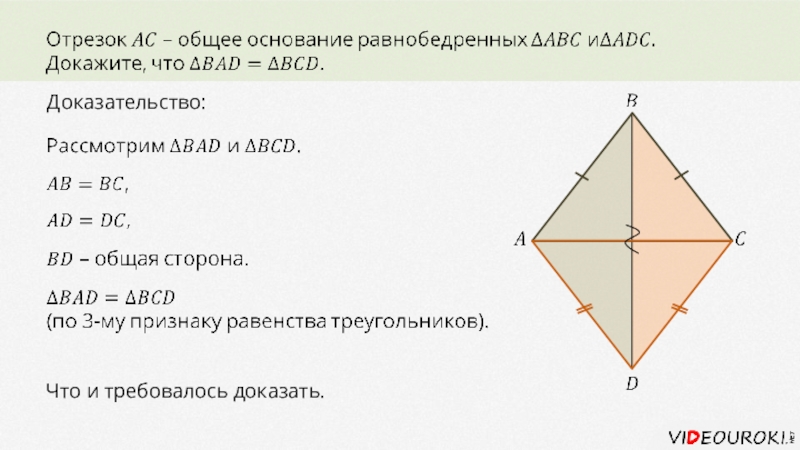
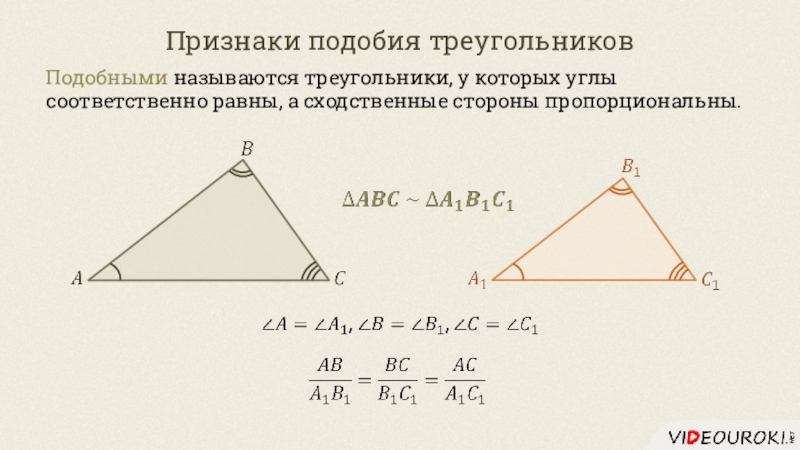
два треугольника равны, то стороны и углы одного треугольника соответственно

В равных треугольниках против соответственно равных сторон лежат равные углы, и наоборот: против соответственно равных углов лежат равные стороны.

между ними одного треугольника соответственно равны двум сторонам и углу

Доказательство

к ней угла одного треугольника соответственно равны стороне и двум

Доказательство

сторона
боковая сторона
Теоремы о свойствах равнобедренного треугольника.
Теорема 1.
В равнобедренном треугольнике

Теорема 2.
В равнобедренном треугольнике биссектриса, проведённая к основанию, является медианой и высотой.

соответственно равны трём сторонам другого треугольника, то такие треугольники равны.
Доказательство

соответственно равны трём сторонам другого треугольника, то такие треугольники равны.
Доказательство

соответственно равны трём сторонам другого треугольника, то такие треугольники равны.
Доказательство

а сходственные стороны пропорциональны.

соответственно равны двум углам другого треугольника, то такие треугольники подобны.
Доказательство
Если

пропорциональны двум сторонам другого треугольника и углы между ними равны,

Доказательство

соответственно пропорциональны трём сторонам другого треугольника, то такие треугольники подобны.
Доказательство