Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
По 239 урок 1
Содержание
- 1. По 239 урок 1
- 2. 1 Можно ли расставить вдоль стен
- 3. Можно. Вариант а) 8 табуреток:
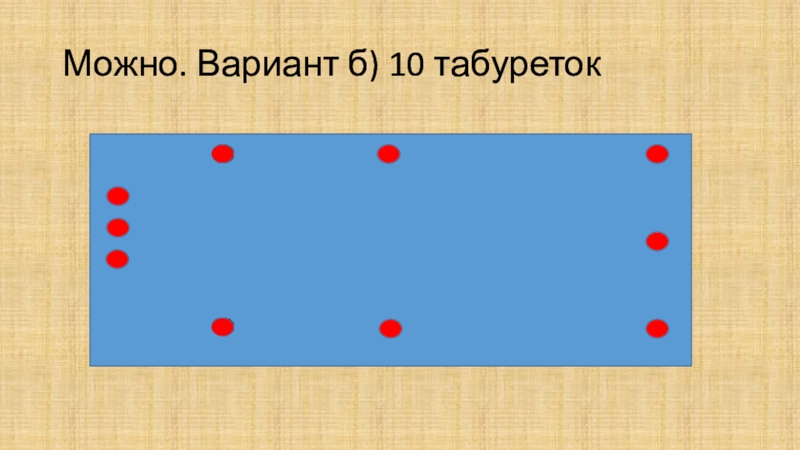
- 4. Можно. Вариант б) 10 табуреток
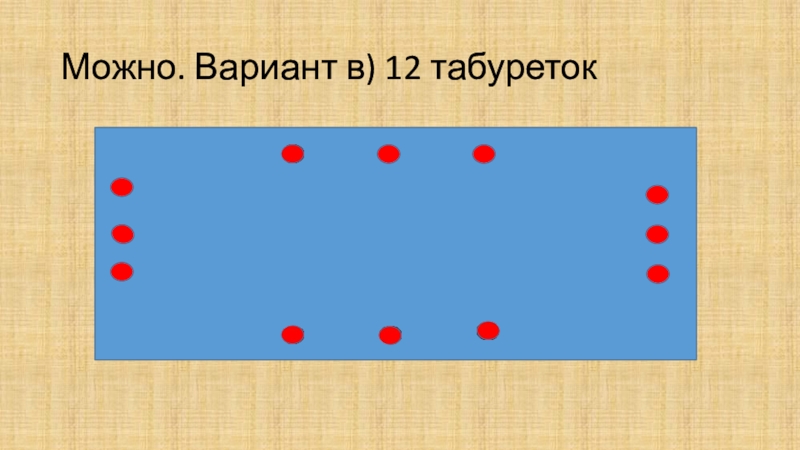
- 5. Можно. Вариант в) 12 табуреток
- 6. 2 После семи стирок длина , ширина
- 7. Если кусок уменьшился по длине, ширине и
- 8. 3 В пещере старый пират разложил свои
- 9. Решение: По условию задачи составим таблицу:
- 10. 4 Девять осликов за 3 дня съедают
- 11. Решение : 1) 27 : 3=
- 12. 5 Кенгуру мама прыгает за 1 секунду
- 13. Решение : 1) 240 : 3 =
- 14. 6 На скотном дворе гуляли гуси и
- 15. Решение : 1) пусть все поросята подняли
- 16. 7 Инженер ежедневно приезжал на станцию в
- 17. Решение: За 10 мин машина проходит путь,
- 18. 8 В триседьмом царстве живут драконы. У
- 19. Решение: Покажем, что у 40% драконов может
- 20. 9 У Гарри Потера имеются двое песочных
- 21. Решение: 15 = (11 - 7) + 11.
- 22. 10 Как отмерить 3 л, имея сосуд
- 23. Решение 1 этап. Наливаем кастрюлю. 2
- 24. 11 Часы Юры отстают на 8 минут,
- 25. РЕШЕНИЕ: Отметим, что мальчики приходят в точку
- 26. 12 Петя в трамвае заметил Васю, который
- 27. РЕШЕНИЕ: Прежде всего, нужно понять, что означает
- 28. Поэтому если за одну минуту Вася проходит
- 29. 13 Cвете втрое больше лет, чем было
- 30. Задачи на возраст удобно показывать на временной
- 31. 14 Всего 5555 человек, на 10
- 32. Решение: Для начала определим, сколько человек в
- 33. 15 В нескольких одинаковых автобусах 115 человек
- 34. Решение: Поскольку мест в автобусах не осталось,
- 35. 16 Как при помощи только пяти цифр
- 36. 0=(5-5) •(5+5+5) 1=5:5+(5-5) •5 2=(5+5):5+5-5 3=(5•5-5-5):5 4=5-5:5+5-5 5=5+(5-5) •(5+5) 6=5+5:5+5-5 7=5+5:5+5:5 8=5+(5+5+5):5 9=(5•5-5):5+5 10=5+5+(5-5) • 5
- 37. 17 Четыре утёнка и пять гусят
- 38. Решение: 4 утенка + 5 гусят=4100грамм 5
- 39. 18 Имеются бревна разной длины. Когда каждое
- 40. Решение: Если бревно распилить на любое
- 41. 19 В день рождения дяди Федора почтальон
- 42. Решение: Заметим, что если не ошибся
- 43. 20 Когда три подруги — Надя, Валя
- 44. Решение: У Вали туфли не синие (по
- 45. 21 В комнате находятся 85 воздушных шаров
- 46. Решение: Поскольку среди двух любых шаров один
- 47. 23 Школьники посадили вдоль дороги (по прямой)
- 48. Решение: 600:24 = 25 дм –
- 49. 24 Вася может получить число 100, используя
- 50. Вместо двоек используйте тройки или семерки. 100=3
- 51. (222 — 22) : 2 = 100
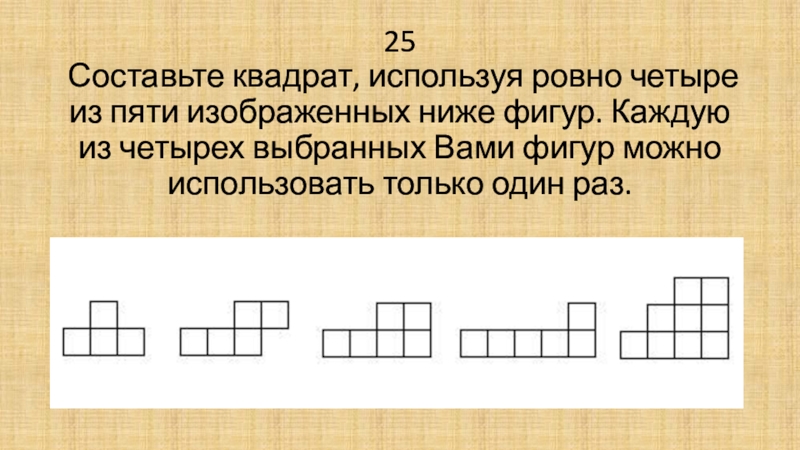
- 52. 25 Составьте квадрат, используя ровно четыре из
- 53. Вырежьте из бумаги данные фигуры и попробуйте сложить квадрат.
- 54. 26 Папа, Маша и Яша идут в
- 55. Решение задачи Рассмотрим отрезок пути, на котором
- 56. 27 Шурик, Трус, Балбес и Бывалый участвовали
- 57. Решение. Ответ: 1. Балбес; 2. Трус; 3.
- 58. 28 В бочке находится не менее 13
- 59. Решение. Наполняем из бочки девятилитровое ведро и
- 60. 29 Количество цифр, потребовавшихся для нумерации всех
- 61. Решение. На однозначные номера потрачено 9 цифр, на
- 62. 30 Коля заплатил 115 руб за четыре
- 63. Решение. Так как покупки Коли и Саши
- 64. 31 Сколько раз к наибольшему однозначному числу надо прибавить наибольшее двузначное число, чтобы получить наибольшее трёхзначное.
- 65. Решение. 9 + 99п = 999 99п
- 66. 32 В примере на сложение двух чисел
- 67. Ответ: 6+2000 = 2006. Если из суммы
- 68. Продолжение следует...
- 69. Скачать презентанцию
1 Можно ли расставить вдоль стен прямоугольной комнаты а) 8; б) 10; в)12 табуреток так,
Слайды и текст этой презентации
Слайд 62 После семи стирок длина , ширина и высота куска мыла
уменьшилась вдвое. На сколько хватит оставшегося куска?
Слайд 7Если кусок уменьшился по длине, ширине и высоте в 2
раза, то по объёму он уменьшился в 8 раз, т.
е. израсходовано 7/8 мыла, а осталась 1/8 мыла. 7/8 куска – 7 стирок 1/8 куска – 1 стирка Ответ: на 1 стирку.Решение:
Слайд 83 В пещере старый пират разложил свои сокровища в 3 цветных
сундука, стоящих вдоль стены: в один - драгоценные камни, а
в другой - золотые монеты, а в третий - оружие. Он помнит, что : - красный сундук правее, чем драгоценные камни - оружие правее, чем красный сундук. В сундуке какого цвета лежит оружие, если зелёный сундук стоит левее, чем синий?Слайд 9Решение: По условию задачи составим таблицу: Драг. к.
?
Оружие Зел. сундук Крас. сундук Син. сундук Ответ: ДК - зелёный ЗМ - красный О - синийСлайд 104 Девять осликов за 3 дня съедают 27 мешков корма. Сколько корма
надо пяти осликам на 5 дней?
Слайд 11Решение : 1) 27 : 3= 9 меш. – съедят 9
осликов за 1 день 2) 9 : 9 = 1
меш. - съест 1 ослик за 1 день 3) 5 * 1 = 5 меш.- съедят 5 осликов за 1 день 4) 5 * 5 = 25 меш. – 5 осликов за 5 дней Ответ: 25 мешковСлайд 125 Кенгуру мама прыгает за 1 секунду на 3 метра, а
её маленький сынишка прыгает на 1 метр за 0,5 секунды. Они
одновременно стартовали от бассейна к эвкалипту по прямой. Сколько секунд мама будет ждать сына под деревом, если расстояние от бассейна до дерева 240 метров.Слайд 13Решение : 1) 240 : 3 = 80 (с) скакала мама
Кенгуру 2)если сын за 0,5 с - 1 м, то за
1 с - 2 м 3) 80 • 2 = 160 (м) проскачет кенгурёнок за 80 с 4) 240 - 160 = 80 (м) осталось проскакать кенгурёнку, когда мама уже под эвкалиптом 5) 80 : 2 = 40 (с) Ответ: 40 секунд.Слайд 146 На скотном дворе гуляли гуси и поросята. Мальчик сосчитал количество голов,
их оказалось 30, а затем он сосчитал количество ног, их
оказалось 84. Сколько гусей и сколько поросят было на cкотном дворе?Слайд 15Решение : 1) пусть все поросята подняли по 2 ноги и
на земле остались стоять только 2 ноги у каждого поросёнка 2)
30 • 2 = 60 ног – столько ног стоят на земле у поросят и гусей вместе 3) 84 - 60 = 24 ноги – подняли поросята 4) 24 : 2 = 12 поросят 5) 30 - 12 = 18 гусей Ответ: 12 поросят и 18 гусей.Слайд 167 Инженер ежедневно приезжал на станцию в одно и то же
время, и в то же время за ним подъезжала машина,
на которой он ехал на завод. Однажды инженер приехал на станцию на 55 мин раньше обычного. Сразу пошел навстречу машине и приехал на завод на 10 мин раньше, чем обычно. Во сколько раз скорость инженера меньше скорости машины?Слайд 17Решение: За 10 мин машина проходит путь, равный двойному расстоянию от
станции до места встречи инженера с машиной. Значит, путь от станции
до места встречи машина проходит за 5 мин. На месте встречи машина была за 5 мин до времени обычного приезда инженера на станцию, значит, путь от станции до места встречи инженер шел 55 мин - 5 мин = 50 мин. Следовательно, скорость инженера в 50 : 5 = 10 раз меньше скорости машины.Слайд 188 В триседьмом царстве живут драконы. У каждого дракона одна, две или
три головы. Может ли у 40 % драконов быть 60
% голов?Слайд 19Решение: Покажем, что у 40% драконов может быть 60% голов. Пусть в
этом царстве живет 100 драконов: 40 драконов с одной головой,
20 – с двумя головами и 40 – с тремя. Тогда число голов у всех драконов равно 40 • 1 + 20 • 2 + 40 • 3 = 200. При этом все 40 трехглавых драконов, что составляет 40% от общего числа драконов, имеют 40 • 3 = 120 голов, что составляет 120/200 • 100% = 60% от общего числа голов.Слайд 209 У Гарри Потера имеются двое песочных часов: на 7 минут
и на 11 минут. Волшебное зелье должно варится 15 минут.
Как сварить его Гарри Потеру, перевернув часы минимальное количество раз?Слайд 21Решение: 15 = (11 - 7) + 11. Нужно одновременно перевернуть часы,
через 7 минут Гарри начинает варить зелье. После 4 минут
(песок в часах на 11 минут закончится) вновь перевернуть часы на 11 минут.Слайд 2210 Как отмерить 3 л, имея сосуд 5 л. Какое наименьшее число
переливаний потребуется для того, чтобы в четырехлитровую кастрюлю с помощью
крана и пятилитровой банки налить 3 литра воды?Слайд 23Решение 1 этап. Наливаем кастрюлю. 2 этап. Переливаем воду из кастрюли в
банку. 3 этап. Наливаем кастрюлю. 4 этап. Доливаем полную банку, и в
кастрюле остается 3 литра.Слайд 2411 Часы Юры отстают на 8 минут, но он считает, что
часы спешат на 2 минуты. Часы Коли спешат на 2
минуты, однако он думает, что они отстают на 8 минут. Друзья договорились встретиться в 5 часов вечера. Кто раньше окажется у места встречи и на сколько минут?Слайд 25РЕШЕНИЕ: Отметим, что мальчики приходят в точку встречи по своему
«внутреннему» таймеру (который рассчитывают), а не по реальному. Поэтому надо
узнать, каково реальное время в момент прихода каждого. 1) Найдем разницу между реальным временем и тем временем, которое представляет себе Юра. Пусть точное время x минут, тогда на часах Юры x-8 минут. Так как он думает, что они спешат, значит считает, что сейчас x-8-2 минут. Поэтому значение реального времени больше того, которое представляет себе Юра на 10 минут. Это означает, что к моменту прихода Юры в точку встречи реальное время составит 17ч 10 мин. 2) Аналогично рассуждая можно получить расклад по Коле. Пусть y (мин) — реальное время. Тогда часы Коли в этот момент показывают y+2 (мин). Так как он думает, что часы отстают на 8 минут, значит считает, что в этот момент y+2+8 минут. Поэтому значение реального времени меньше представляемого Колей на 10 минут. Это значит, что к моменту прихода Коли реально 16ч 50 мин. Ответ: Коля пришел раньше Юры на 20 минут.Слайд 2612 Петя в трамвае заметил Васю, который поравнялся с трамваем, следуя
вдоль трамвайных путей в противоположном направлении. Через минуту Петя вышел
и побежал вдогонку за Васей вдвое быстрее его, но в 4 раза медленнее трамвая. Через какое время Петя догонит Васю? Помогите.Слайд 27РЕШЕНИЕ: Прежде всего, нужно понять, что означает «в два раза
быстрее». Это значит, что скорость больше в два раза. А
поэтому в два раза больше будет пройденное расстояние (не важно, за какое время). Тогда, если Петя идет в два раза быстрее Васи и в 4 раза медленнее трамвая, то Вася проходит за минуту в 4•2=8 раз меньшее расстояние, чем трамвай.Слайд 28Поэтому если за одну минуту Вася проходит какой-то отрезок пути,
то трамвай проезжает 8 таких отрезков. Поэтому расстояние между мальчиками
в момент выхода Пети составляет 9 отрезков. За ту же минуту Петя проходит 2 отрезка (раз его скорость в 2 раза больше). Введем единицу измерения длины, равную этому же отрезку. Тогда мы имеем стандартные начальные данные для самой обычной задачи на скорость сближения. Скорости мальчиков известны – это 1 (отрезок/мин) и 2 (отрезка/мин), а расстояние для сближения составляет 9 отрезков.За каждую минуту оно сокращается на 2-1=1 отрезок (это и есть скорость сближения). А нам надо узнать, за какое время расстояние в 9 отрезков сократится до нуля, то есть надо узнать время сближения. Его можно найти, разделив путь сближения на скорость сближения. Поэтому 9 делим на 1 и получаем 9 минут.
Ответ: 9 мин.
Слайд 2913 Cвете втрое больше лет, чем было Максиму тогда, когда она
была в его нынешнем возрасте. Когда Максим будет в возрасте
Светы, то им вместе будет 28лет. Сколько сейчас лет Максиму и сколько сейчас лет Свете?Слайд 30Задачи на возраст удобно показывать на временной оси, на которой
возраста представляются точками. Если у нас 2 человека и их
возраста меняются, то изображающие их точки будут просто двигаться по оси. При этом расстояние между ними (разница в возрасте) будет сохраняться. Покажем нынешний возраст Светы и Максима точками С и М (верхний ряд букв на рисунке). В нижнем ряду поставим буквы С и М для того момента, когда «Света была в нынешнем возрасте Максима». Получим равные отрезки, концы которых (нижняя М и верхняя С) согласно условию «в 3 раза» можно обозначить как х и 3х. Тогда нынешний возраст Максима (середина отрезка) будет иметь координату 2х, а значит разница в возрасте составит ровно х (лет). Теперь покажем, какими будут координаты возрастов в тот момент, когда Максим окажется в возрасте Светы. Эти буквы стоят в ряду «будущее». Длина их отрезка тоже равна х (лет) и поэтому возраст Светы в этот момент окажется равным 4х (лет). Так как в будущем им вместе будет 28 лет, то 3х+4х=28, откуда получаем, что х=4. Поэтому Максиму сейчас 2*4=8 лет , а Свете сейчас 3*4=12 летСлайд 3114 Всего 5555 человек, на 10 солдат приходится 1 капрал, на
5 капралов 1 офицер, на 9 офицеров 1 генерал. Сколько
всего было солдат?Слайд 32Решение: Для начала определим, сколько человек в одном таком «наборе»,
состоящем из генерала, капралов, офицеров и солдат. Один генерал и девять
офицеров у нас уже есть. Так как на каждого офицера приходится 5 капралов, то на 9 офицеров приходится 9*5= 45 капралов.Так как на каждого капрала приходится 10 солдат, то на 45 капралов приходится 45*10 =450 солдат
Всего в наборе 1+9+45+450=505 человек
Так как всего в армии 5555 человек, то количество наборов равно 5555:505=11. В одном наборе 450 солдат , поэтому
в 11 наборах будет 11*450=4950 солдат.
Ответ : 4950 солдат.