Слайд 1Побудова загальної лінійної економетричної моделі
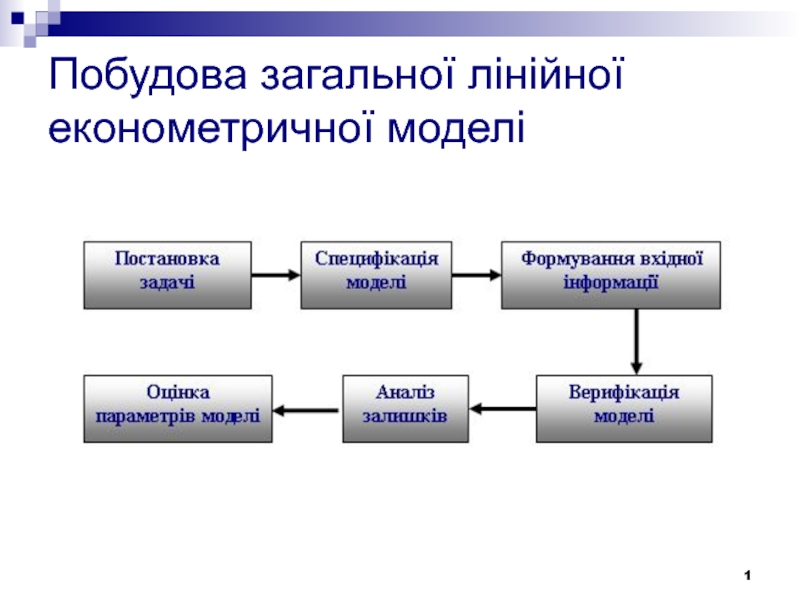
Слайд 2Крок 1. Знайомство з економічною теорією, висунення гіпотези взаємозв'язку. Чітка
постановка задачі.
Крок 2. Специфікація моделі. Використовуючи всі ті форми функцій,
які можуть бути застосовані для вивчення взаємозв'язків, необхідно сформулювати теоретичні уявлення і прийняті гіпотези у вигляді математичних рівнянь. Ці рівняння встановлюють зв'язки між основними визначальними змінними за припущення, що всі інші змінні є випадковими.
Крок 3. Формування масивів вхідної інформації згідно з метою та завданнями дослідження.
Слайд 3Крок 4. Оцінка параметрів економетричної моделі методом найменших квадратів. Аналіз
залишків дає змогу відповісти на запитання: чи не суперечить специфікація
моделі передумовам «класичної» моделі лінійної регресії?
Крок 5. Якщо деякі передумови моделі не виконуються, то для продовження аналізу треба замінювати специфікацію або застосовувати інші методи оцінювання параметрів.
Крок 6. Проведення аналізу достовірності моделі та прогнозу за побудованою моделлю.
Слайд 4ПАРНА ЛІНІЙНА РЕГРЕСІЯ
МЕТОД НАЙМЕНШИХ КВАДРАТІВ
Лекція 5
Слайд 5У загальному випадку парна лінійна регресія є лінійною функцією між
залежною змінною Y і однією пояснюючою змінною X:
Y=a0+a1X.
Співвідношення називається
теоретичною лінійною регресійною моделлю;
a0 a1 — теоретичні параметри (теоретичні коефіцієнти) регресії.
принциповою в цьому разі є лінійність за параметрами a0 і а1
Слайд 6Щоб визначити значення теоретичних коефіцієнтів регресії, необхідно знати й використовувати
всі значення змінних X і Y генеральної сукупності ( що
практично неможливо).
Тому за вибіркою обмеженого обсягу будують так зване емпіричне рівняння регресії, у якому коефіцієнтами є оцінки теоретичних коефіцієнтів регресії:
де оцінки невідомих параметрів а1 і а0
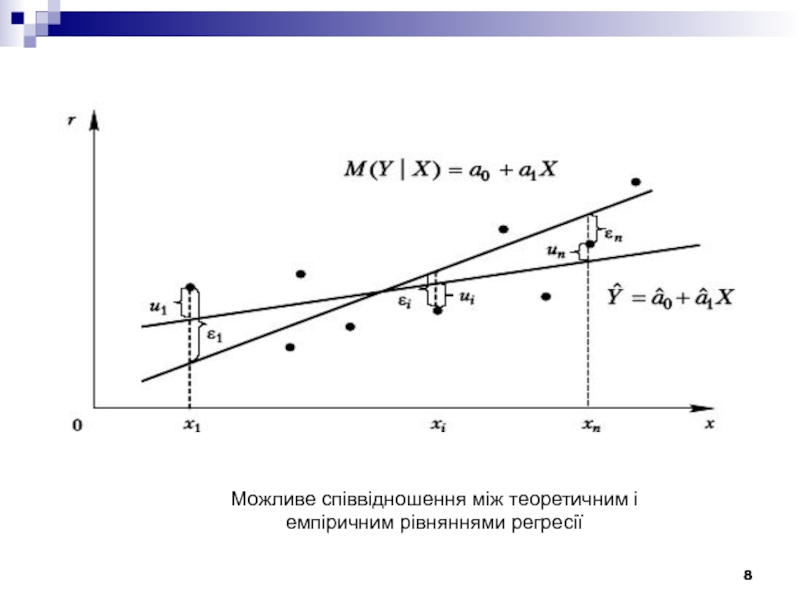
Слайд 7Через розбіжність статистичної бази для генеральної сукупності та вибірки оцінки
â0 і â1 практично завжди відрізняються від дійсних значень коефіцієнтів
а0 а1, що призводить до розбіжності емпіричної та теоретичної ліній регресії.
Різні вибірки з однієї й тієї самої генеральної сукупності звичайно зумовлюють різні оцінки
Слайд 8Можливе співвідношення між теоретичним і емпіричним рівняннями регресії
Слайд 9Задачі лінійного регресійного аналізу полягають у тому, щоб за наявними
статистичними даними (xi ,yi), i=1,2,..., n, для змінних X і
Y:
а) отримати найкращі оцінки â0 â1 невідомих параметрів а0 і a1,:
б) перевірити статистичні гіпотези щодо параметрів моделі;
в) перевірити, чи досить добре модель узгоджується зі статистичними даними (адекватність моделі даним спостережень).
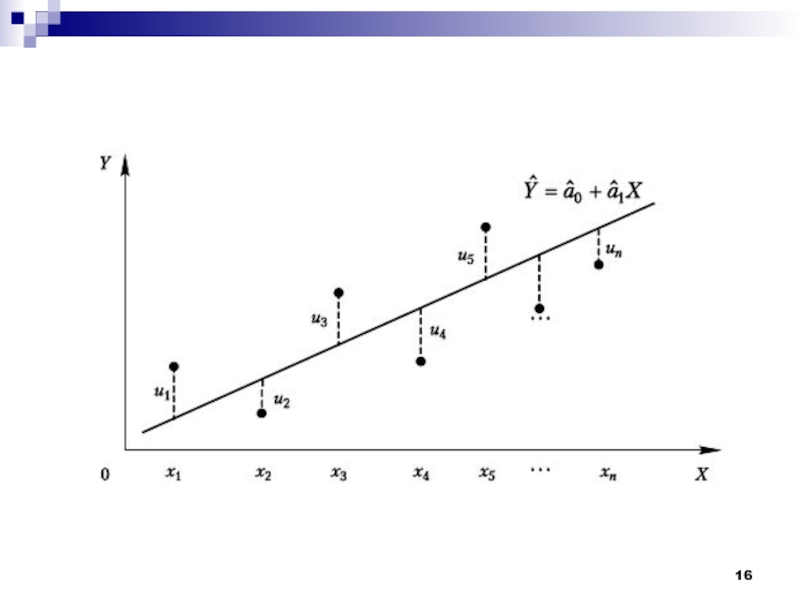
Слайд 10Для відображення того факту, що кожне індивідуальне значення уі відхиляється
від відповідного умовного математичного сподівання, у модель уводять випадкову складову
ui
yi=M(Y | X = xi )+ui =a0+a1xi + ui
Iндивідуальні значення уі складається з суми двох компонент — систематичної (a0+a1xi) і випадкової ui
Слайд 11Регресійне рівняння набуває вигляду
Y =а0+а1Х+и
Завдання полягає в тому, щоб
за конкретною вибіркою (xi, yi), і = 1,2..... n, знайти
такі значення оцінок невідомих параметрів a0 і a1, щоб побудована лінія регресії була найкращою ("найближчою" до точок спостережень за їх сукупністю) серед усіх інших прямих.
Мірою якості знайдених оцінок можуть бути визначені композиції відхилень
ui, i=1, 2,..., n.
Слайд 12Наприклад, коефіцієнти a0 і a1 рівняння регресії можуть бути оцінені
за умови мінімізації однієї з таких сум:
Слайд 131) Перша сума не може бути мірою якості знайдених оцінок
а через те, що існує безліч прямих (зокрема, У =
у ), для яких.
2) Метод визначення оцінок коефіцієнтів за умови мінімізації
називається методом найменших модулів (МНМ).
3) Найпоширенішим і теоретично обгрунтованим є метод визначення коефіцієнтів, при якому мінімізується
носить назву метод найменших квадратів (МНК).
Слайд 14Серед інших методів визначення оцінок коефіцієнтів регресії виділяють метод моментів
(MM) і метод максимальної правдоподібності (MMП).
Слайд 15Метод найменших квадратів (НМК)
Нехай за вибіркою (xi, yi), і =
1,2..... n, потрібно визначити оцінки â0 і â1 емпіричного рівняння
регресії
тобто підібрати такі значення коефіцієнтів рівняння, щоб сума квадратів відхилень була мінімальною
Слайд 17У цьому разі
є квадратичною функцією двох параметрів â0 і
â1, оскільки відомі дані спостережень:
квадратична функція Q неперервна, опукла та
обмежена знизу (Q ≥ 0), тобто має мінімум.
Слайд 18Необхідною умовою існування мінімуму неперервно диференційованої функції двох змінних є
рівність нулю її частинних похідних:
Слайд 19Поділивши обидва рівняння системи на n, отримаємо
Слайд 20Згідно з МНК оцінки параметрів â0 та â1 визначаються за
формулами
â1 можна обчислити за формулою
Слайд 21
вибірковий кореляційний момент випадкових величин X та Y
вибіркова дисперсія
Х
Слайд 22тоді
де rxy – стандартний коефіцієнт кореляції
Sy - стандартне відхилення У
Отже, коефіцієнт регресії пропорційний коефіцієнту кореляції, а коефіцієнти пропорційності використовують
для зіставлення різних величин X і Y.
Слайд 23Таким чином, якщо коефіцієнт кореляції rxy вже розрахований, то неважко
знайти коефіцієнт â1 парної регресії.
Якщо окрім рівняння регресії Y на
X
для тих самих емпіричних даних знайдено рівняння регресії X на Y
то добуток коефіцієнтів â1 та дорівнює rxy2
.
Слайд 24Оцінки параметрів моделі або коефіцієнти регресійної моделі, обчислені методом найменших
квадратів, будуть незміщеними, ефективними, і спроможними, якщо виконуються передумови методу
найменших квадратів.
Незміщенність коефіцієнтів моделі полягає в тому, що математичні сподівання коефіцієнтів моделі рівні параметрам моделі при будь-якому обсязі вибірки.
Ефективність коефіцієнтів моделі полягає в тому, що коефіцієнти мають найменші дисперсії в класі всіх лінійно-незміщенних оцінок.
Спроможність коефіцієнтів моделі полягає в тому, що зі збільшенням обсягу вибірки значення коефіцієнтів наближаються до істинних розмірів цих коефіцієнтів або параметрів моделі.
Слайд 25Передумови методу найменших квадратів
залежна змінна має бути випадковою;
змінні можуть
бути випадковими або детермінованими, але обов'язково змінюваними;
дисперсії залишків моделі мають
бути сталими для кожного фіксованого значення змінної;
Слайд 26автокореляція між залишками має бути відсутньою;
залишки мають розподілятись за нормальним
законом;
кількість чинників у моделі має бути менше обсягу вибірки;
між залишками
і пояснювальними змінними не повинно бути зв'язку;
чинники, що включаються в модель, не повинні бути пов'язаними між собою.